二叉树重点突破

文章目录

一、两个数是否相同

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。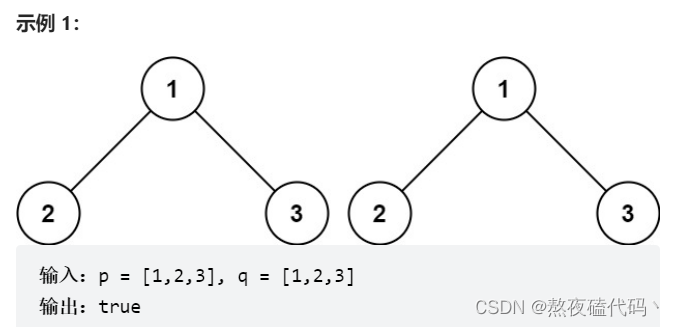


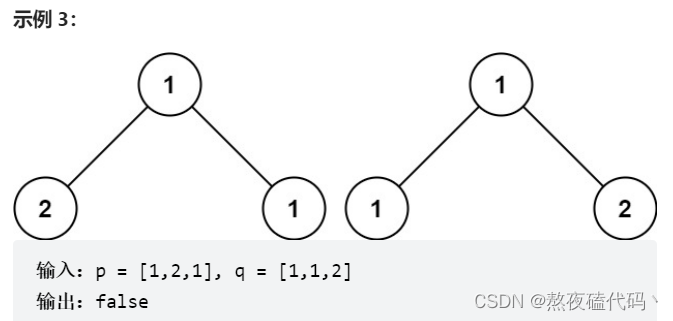
基本思路：
对二叉树进行遍历，判断每一个结点的结构和数值是否相同，不同直接返回false，否则继续判断左子树和右子树直到二叉树遍历完成为止。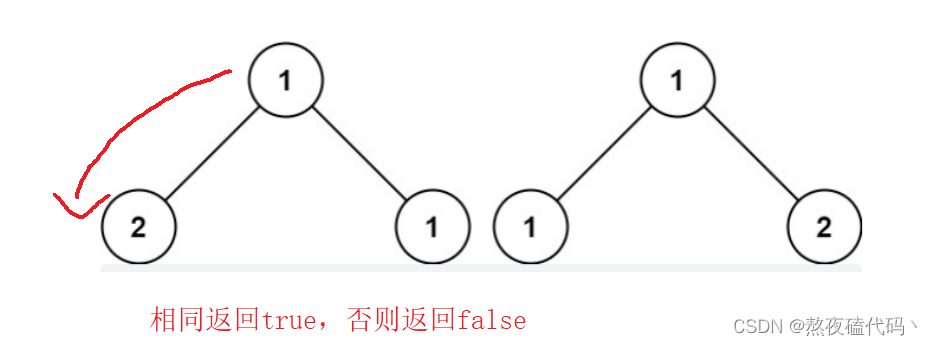

publicbooleanisSameTree(TreeNode p,TreeNode q){//相同的树if(p ==null&& q !=null|| p !=null&& q ==null){returnfalse;}if(p ==null&& q ==null){returntrue;}if(p.val != q.val){returnfalse;}returnisSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}

二、另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

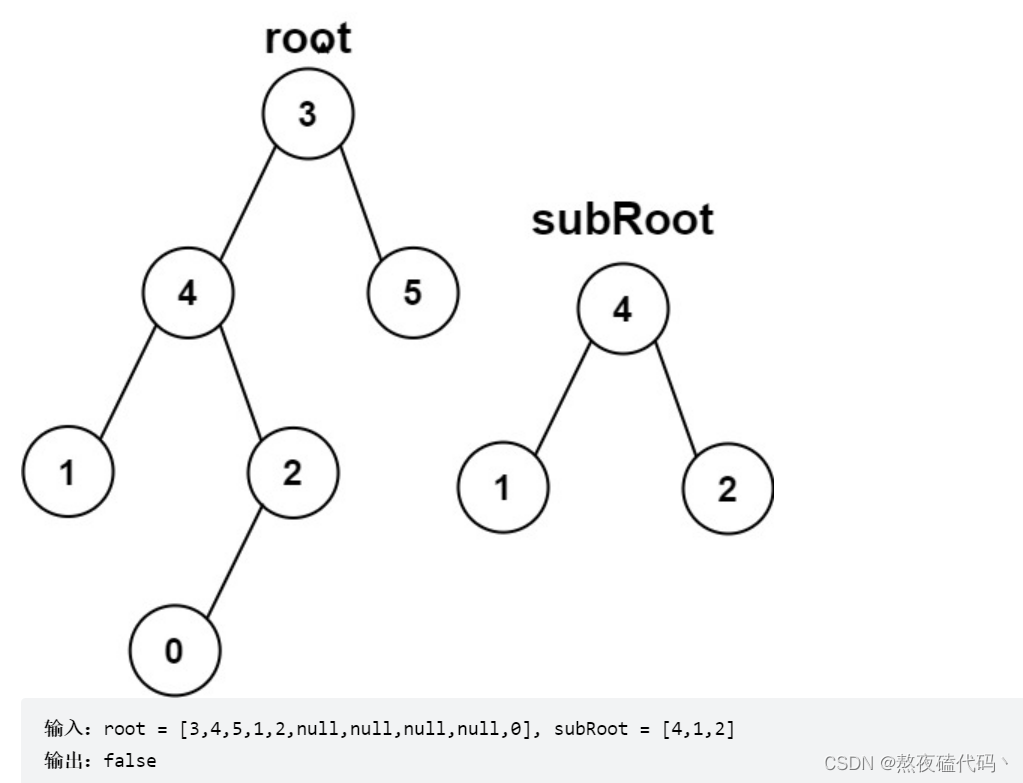
基本思路：
遍历root每一个结点去和子树subRoot去判断是否为相同的树，如果相同返回true，否则继续遍历，如果遍历结束还没有找到，那就返回false,这里可以复用上一题相同树的代码。

publicbooleanisSubtree(TreeNode root,TreeNode subRoot){if(root ==null|| subRoot ==null){returnfalse;}if(isSameTree(root,subRoot)){returntrue;}boolean flg1 =isSubtree(root.left,subRoot);if(flg1 ==true){returntrue;}boolean flg2 =isSubtree(root.right,subRoot);if(flg2 ==true){returntrue;}returnfalse;}publicbooleanisSameTree(TreeNode p,TreeNode q){//相同的树if(p ==null&& q !=null|| p !=null&& q ==null){returnfalse;}if(p ==null&& q ==null){returntrue;}if(p.val != q.val){returnfalse;}returnisSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}

三、二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

解题思路：
这里我们采用子问题方法，将二叉树的最大深度分解为左子树的最大深度和右子树最大深度的最大值+1即为本二叉树的最大深度。

publicintmaxDepth(TreeNode root){if(root ==null){return0;}if(root.left ==null&& root.right ==null){return1;}int leftMax =maxDepth(root.left);int rightMax =maxDepth(root.right);return leftMax > rightMax ? leftMax +1: rightMax +1;}

四、平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为： 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。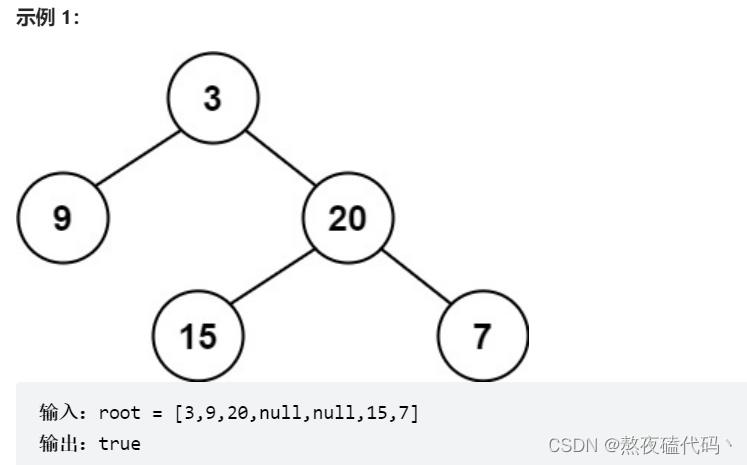


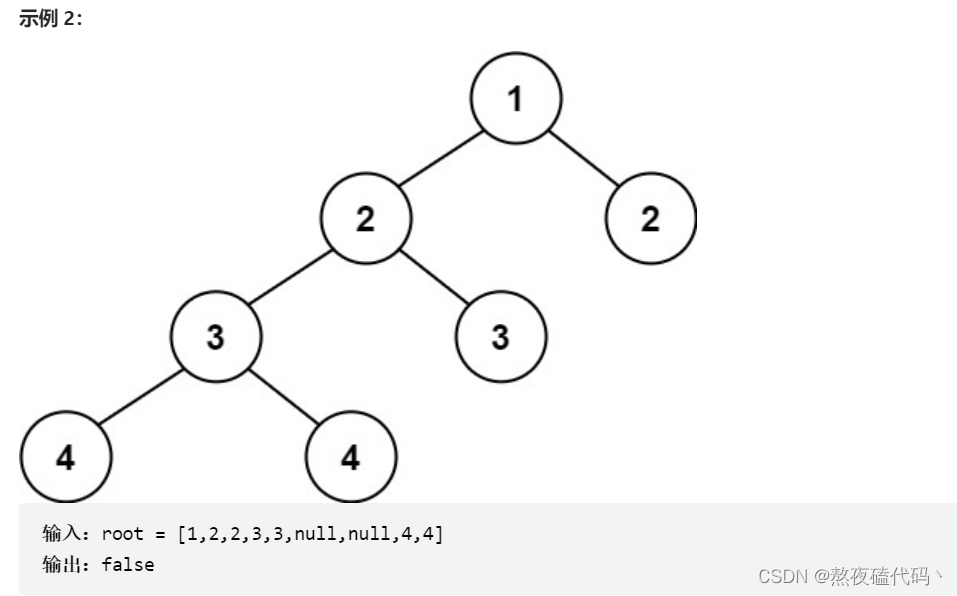
基本思路：
遍历二叉树，去判断二叉树每个结点的左右子树的高度差，如果小于2那么在判断左子树和右子树，如果有任何一个结点不满足，那么就不是平衡二叉树，如果每一个结点都满足那么就是平衡二叉树。

publicbooleanisBalanced(TreeNode root){if(root ==null){returntrue;}int left =maxDepth(root.left);int right =maxDepth(root.right);returnMath.abs(left - right)<2&&isBalanced(root.left)&&isBalanced(root.right);}publicintmaxDepth(TreeNode root){if(root ==null){return0;}if(root.left ==null&& root.right ==null){return1;}int leftMax =maxDepth(root.left);int rightMax =maxDepth(root.right);return leftMax > rightMax ? leftMax +1: rightMax +1;}

这样显然可以达到目的，但是时间复杂度达到了O(n²),能不能O(n)就完成目标呢？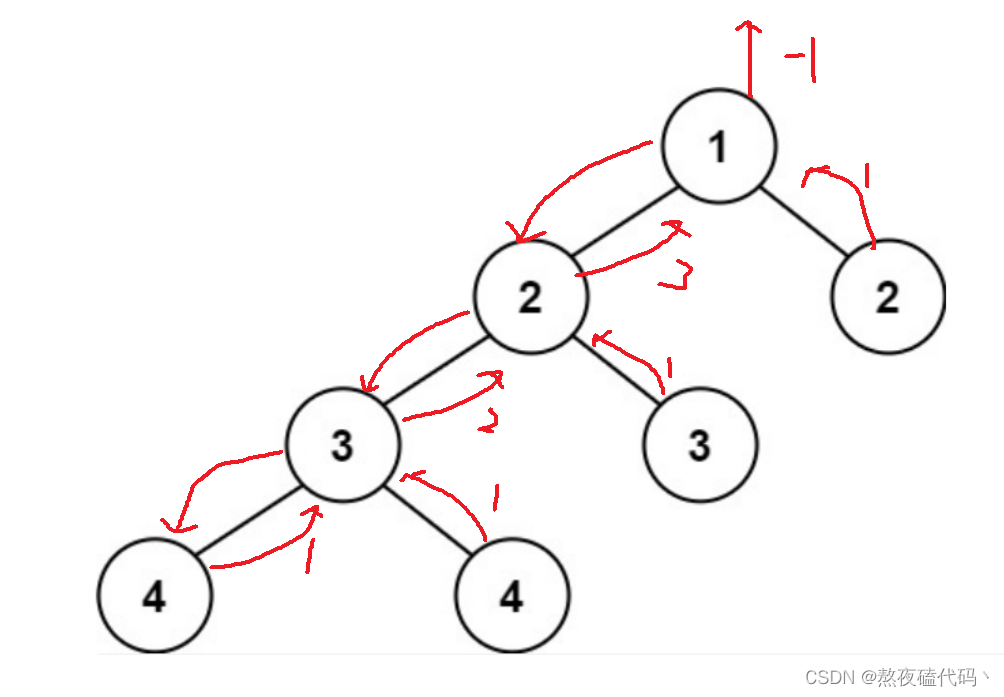

我们对每个结点进行左子树和右子树高度进行计算，如果左右子树的高度差大于1那么直接返回-1，否则继续计算结点的高度。

publicbooleanisBalanced(TreeNode root){if(root ==null){returntrue;}returnmaxDepth1(root)>0;}publicintmaxDepth1(TreeNode root){if(root ==null){return0;}if(root.left ==null&& root.right ==null){return1;}int leftMax =maxDepth1(root.left);int rightMax =maxDepth1(root.right);if(leftMax <0|| rightMax <0||Math.abs(leftMax - rightMax)>1){return-1;}else{returnMath.max(leftMax,rightMax)+1;}}

五、对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。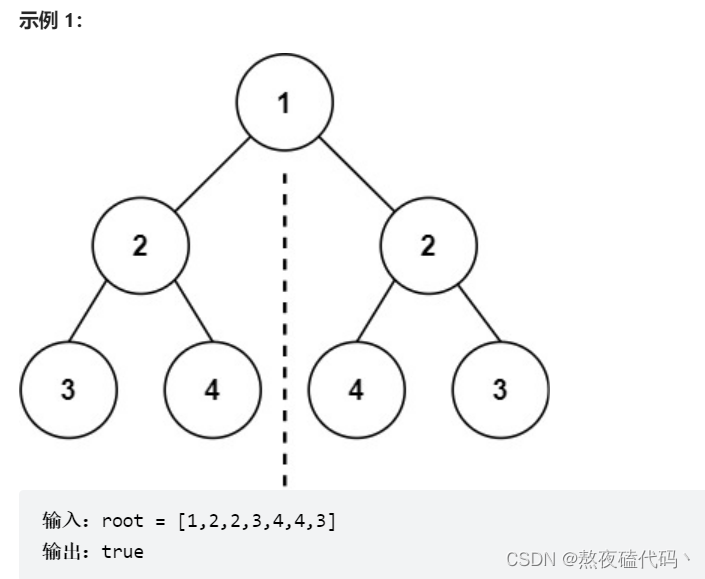


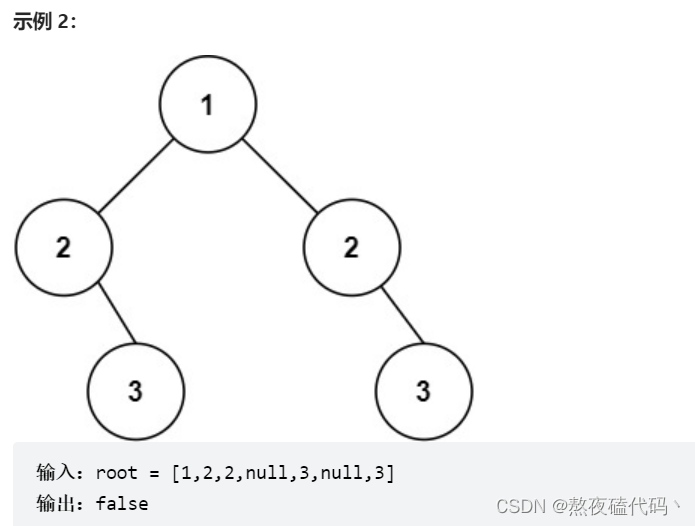
基本思路：
二叉树是否对称分解为左子树和右子树是否对称相等，然后在左子树的左节点和右子树的右节点，左子树的右节点和右子树的左节点是否相等。

publicbooleanisSymmetric(TreeNode root){if(root ==null){returntrue;}returnisSame(root.left,root.right);}publicbooleanisSame(TreeNode left,TreeNode right){if(left ==null&& right !=null|| left !=null&& right ==null){returnfalse;}if(left ==null&& right ==null){returntrue;}if(left.val != right.val){returnfalse;}returnisSame(left.left,right.right)&&isSame(left.right,right.left);}