1. 前言
本文编译自斯坦福大学的CS231n课程(2022) Module1课程中神经网络部分的内容:
【1】Neural Networks Part 2: Setting up the Data and the Loss
2. Modelling One neuron
To be added.
3. Neuron Network architecture
To be added.
4. Setting up the data and the model
4.1 数据预处理
以下,以形状为
[N x D]的矩阵X表示输入数据集,
N
表示样本数据个数,
D表示样本数据维度
( dimensionality)。
主要有三种数据预处理技术。
4.1.1 零均值化 Mean subtract
对数据的每一个feature进行零均值化,具体来说,就是针对每一个feature,求其平均值,然后将所有样本的各feature值减去对应feature的平均值,这样处理后各feature的均值都变为0。
这一处理的几何意义是将数据的各个维度都挪(平移)到以坐标原点为“中心”的区域。在numpy中可以如下实现:
X -= np.mean(X, axis = 0)
在图像处理中,通常进一步简化为
X -= np.mean(X)
, 即不是针对每个feature独立地做,而是所有feature一起做(这可能是基于这样的假设:图像数据的所有各feature的均值基本一致?),或者针对三个通道分别独立地执行。
4.1.2 归一化 Normalization
一般而言,归一化是指将所有各个feature的数据变换成大抵相同的幅度。
一种做法是针对每个feature,将它们变成单位标准方差的分布。用numpy代码来表示就是(假定已经做过零均值化处理了):
X /= np.std(X, axis = 0)
另一种做法是将各feature的数据转换到区间[-1,1]。
归一化处理在什么场合瞎需要呢?当你认为每个feature(数据的各个维度)的数据幅度不同,但是它们对于学习算法来说又应该具有相等的重要性。图像数据通常各个维度的数据幅度范围大抵相当,所以对于图像数据处理而言这个归一化处理并不是必须的。虽说不是必须,但是实际上通常是做的。
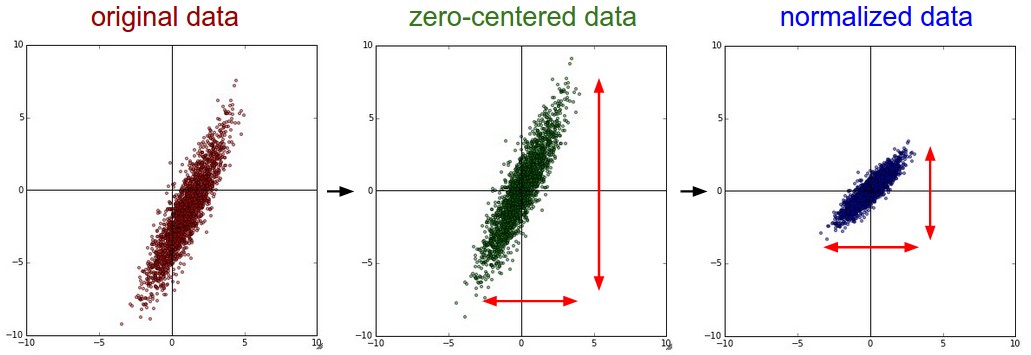
图1 左:原始数据;中:零均值化处理后;右:归一化处理后
4.1.3 PCA and whitening
PCA是指主成分分析(Principal Companent Analysis)。
这个数据预处理方法的基本步骤如下:
Step1:零均值化
Step2:计算协方差矩阵(covaraince matrix)cov
Step3:对协方差矩阵进行SVD分解
Step4:将数据投影到协方差矩阵cov的本征向量张成的空间上得到Xrot。这一步中可以取全部本征向量,也可以取最大的一部分本征向量。这一处理被称为PCA。
Step5:对Xrot进行归一化,这一步称为白化(whitening) - The geometric interpretation of this transformation is that if the input data is a multivariable gaussian, then the whitened data will be a gaussian with zero mean and identity covariance matrix. 这个变化的几何解释是:如果输入数据时多变量高斯分布的话,白化后的数据将是零均值且具有单位协方差矩阵
以下是numpy示例代码:
# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix
U,S,V = np.linalg.svd(cov)
Xrot = np.dot(X, U) # decorrelate the data
# 这个通常称为PCA,下一步whitening可以用PCA也可以用Xrot_reduced
Xrot_reduced = np.dot(X, U[:,:M])
# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + alpha)
Warning:白化处理的一个缺点是会放大噪声,因为这一处理试图将所有维度都转换到相同幅度,包括一些几乎是纯噪声的方差很小的维度。这一缺点类似于通信信号处理中的Zero-Forcing均衡。上式中alpha是一个很小的数,适用于防止除以0的错误。增大alpha有助于缓解这一问题。PCA及白化处理效果的如下所示:
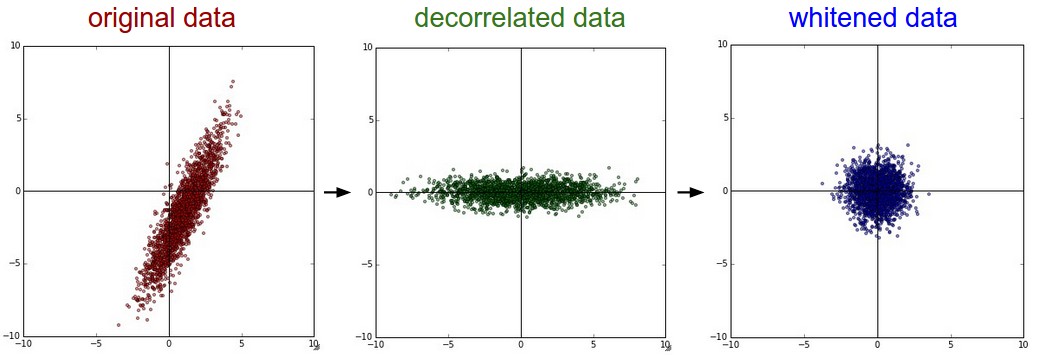
图2 左:原始数据;中:PCA处理后;右:白化后
实际上,虽然PCA&whitening在传统的机器学习领域比较常见,但是在卷积神经网络(CNN)中并不采用这一技术。零均值化对于CNN非常重要,归一化处理虽非必须但是也非常常见。
重要提示:预处理统计量(均值、方差)只能在训练集上计算!然后直接使用于验证集和测试集。
4.2 权重初始化 Weight Initialization
4.2.1 不能做什么
在考察应该如何做之前,首先,我们先强调不能怎么做。
**不能做全零初始化**。借用一句物理学中专业术语来表述的话,神经网络需要对称性破缺(*symmetry breaking*)才能变得有活力。全零初始化导致每个神经元在初始化时输出相同的结果,因而会产生相同的梯度,然后会得到相同的更新。。。然后整个神经网络就一直沉陷于这种完全均匀处处保持相同的状态,了无意趣。
4.2.2 随机的小数值初始化
既希望打破对称性,又希望初始化的权重参数相对较小(因为权重越大意味着模型越复杂!),所以一个常规的做法就是用随机数来进行权重参数随机化,通常采用正态分布或者均一分布均可,如以下numpy代码所示:
W = 0.01* np.random.randn(D,H)
以上使用0.01作为标准偏差,但是是不是越小越好呢?并不是,初始化值太小的话,会导致类似于“gradient diminishing”的问题,特别是对于层数很多的深度网络。
4.2.3 方差调节(calibrating the variances with 1/sqrt(N))
上一节所述方法的一个缺陷是,指定了一个固定的方差。但是,随机初始化的神经网络层的输出的分布的方差会随着该神经网络层输入数据个数(fan-in)的增大而增大。因此有必要把这个因素考虑到参数初始化时的方差选择上,让参数初始化分布的方差随神经网络层输入数据个数(fan-in)的变化而自适应式地变化。一个推荐方案如下所示:
w = np.random.randn(n) / sqrt(n)
其中,n表示当前网络层的输入数据个数。 这样的初始化策略使得每一层在初始化后的输出的分布有大致相同的方差,实践表明这样能够有效地提高收敛速度(rate of convergence)。
Glorot 的论文给出了的建议是(大同小异):
w = np.random.randn(n) * sqrt(2)/ sqrt(Nin+Nout)
He et al的论文中则给出了使用ReLU激励函数时的建议为:
w = np.random.randn(n) * sqrt(2.0/n)
由于ReLU也是目前神经网络中最常用的激励函数,因此He et al的建议也成了目前最常用的初始化方案。
4.2.4 稀疏初始化
另外一种权重参数初始化方案是使得每个神经元与它的下一层的所有的神经元节点之间,随机选择少数神经元将其权重参数用从高斯分布中采样的较小的数进行初始化,而其它则全部初始化为0。通常非零初始化的权重参数小于10个。
4.2.5 偏置初始化
与权重参数不同的话,偏置参数通常初始化为0。虽然也有人喜欢以权重参数相同的方式初始化偏置参数,但是并没有证据表明这样做有什么显著的好处。
4.2.6 Batch Normalization
BatchNormalization(批归一化)处理是由Ioffe and Szegedy所提出的一项技术,它大大缓解了由于不适当的权重参数初始化所带来的问题(意味着神经网络研究者不必那么绞尽脑汁地去钻权重参数初始化的牛角尖了)
其做法是在每一个全连接层或卷积层与随后的激活层之间插入一个BatchNorm,针对该层的每一个批次的数据处理输出结果都进行一次归一化处理。BatchNorm也可以看作是作为每一层神经网络的预处理,但是又是以可微分的方式集成到了神经网络中,简洁而优雅!
4.3. Regularization
正则化技术是用于控制网络的复杂度以防止过拟合的技术。
4.3.1 L2 regularization
L2正则化是最常用的正则化技术。 针对每一个权重参数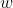,给目标函数加一项作为惩罚项。其中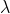表示正则化强度(regularization strength)。“1/2”因子并非必须,仅是用于抵消平方项的梯度计算带来的因子2。L2正则化的直观解释是抑制尖峰式的权重参数,迫使权重参数分布扩散化(diffusing);换句话,迫使神经网络尽量使用所有的数据,给每个输入数据一个较小的权重,而不是给少数的输入数据明显大于其它输入数据的权重。通俗一点说,就是L2正则化导致一个更加“民主”的神经网络。
最后,要注意到,由于梯度更新,使用L2正则化意味着每个权重参数是以线性的方式衰减至零:
W += -lambda * W。
4.3.2 L1 regularization
L1正则化是另一种相对也较常用的正则化技术。 针对每一个权重参数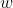,给目标函数加一项,同样, 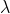表示正则化强度(regularization strength)。也有把L1正则化和L2正则化结合起来使用的,即惩罚项为 (这个也称之为 Elastic net regularization)。L1正则化有一个很好的特性是它会导致权重参数稀疏化,即只有很少的一部分权重参数为非0,大部分权重参数都为0。换句话说,只有少数最重要的输入对输出有影响,而其它大部分输入都被当作噪声而被忽略了。
在实践中,如果你不是很关注显式的特征选择的话,L2正则化通常能取得远远好于L1正则化的性能。或者说,L2正则化更通用,而L1正则化则会用于某些特定的场合。
4.3.3 Max Norm constraints
另外一种正则化措施是对权重参数的幅度绝对值施加一个上限(upper bound),实现这一目的的手段是采用投影梯度下降(projected gradient descent)方法。实际上,这个相当于是按以下两步来进行参数更新:
(1) 按正常的方式进行参数更新各参数
(2) 对各神经元的权重参数向量进行钳位(clamping)处理使其满足。c的大小通常选择在3~4之间
有些研究者报告说使用这种正则化技术获得了性能提升。这种正则化技术的一个有利的特性在于即便学习率(learning rate)设得过高,也不会导致网络“爆炸(explode)”,因为权重参数始终是受限的。
4.3.4 Dropout
Dropout是由Srivastava在其论文中引入的作为以上提及的其它正则化方法的一种非常简单而且有效的正则化方法。在训练过程中,按概率随机地选择一部分神经元保留为活跃状态,其它则置为不活跃(等价于切断它们的连接)。.
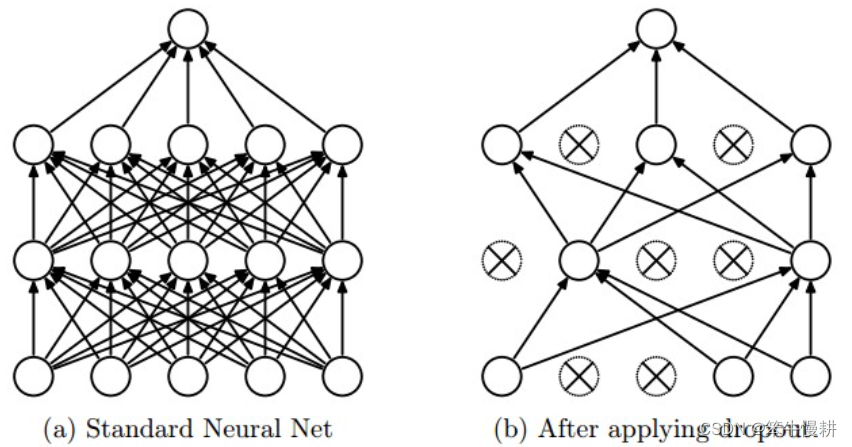
图3 左:标准的网络;右:实施Dropout后
Dropout可以理解为,对一个完全网络进行随机性的采样得到不同的子网络。每个epoch甚至每个mini-batch的采样都不同,换句话说,每个epoch甚至每个mini-batch针对不同的子网络进行训练。
注意,Dropout在测试阶段是被关闭的。测试阶段所使用的网络可以看作是所训练的所有子网络的统计平均(ensemble average)。
Vanilla Dropout实现方案如下(Vanilla大致意指naive,傻傻的意思):
""" Vanilla Dropout: Not recommended implementation (see notes below) """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
""" X contains the data """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) < p # second dropout mask
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
out = np.dot(W3, H2) + b3
在以上代码中,在
train_step()函数中在第一层和第二层分别执行了一次dropout(通过用mask函数U1和U2与各神经元输出进行element-wise相乘来实现)。当然也可以针对输入层执行dropout
。backward pass处理以上没有列出,但是当然也需要把所生成mask
U1,U2考虑进去
.
关键的是,在
predict()函数中没有drop任何东西。取而代之的是,对两个在forward pass中执行了dropout的隐藏层的输出实施了基于dropout参数的scaling处理,在train阶段由于dropout导致每个神经元的输入连接的神经元个数降低并进而导致该神经元输出值相应减小,在test中(没有dropout每个神经元可以看到它的全部输入神经元)进行相应的scaling处理会使得每个神经元的输出的期望与train阶段各神经元输出的期望相同。
这种做法的一个缺点是必须在进行prediction(预测或推断inference)的时候执行这一scaling处理。而通常来说,prediction时的系统(吞吐率)性能是至关重要的,能否将这一处理吸收到训练阶段去呢。研究者为此提出了
inverted dropout方法, 在train期间实施必要的scaling处理。这样做的好处不仅仅是省掉了在prediction阶段的额外的运算量,而且当你想调节dropout机制时,由于它已经完全吸收在train阶段的处理中了,你不需要对prediction处理作任何修改。Inverted dropout的实现代码如下所示:
"""
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
H2 = np.maximum(0, np.dot(W2, H1) + b2)
out = np.dot(W3, H2) + b3
在Dropout被初次引入后有大量的研究跟进试图理解Dropout的威力的来源以及它与其它正则化化方法的关系,感兴趣者推荐进一步阅读:
- Dropout paper by Srivastava et al. 2014.
- Dropout Training as Adaptive Regularization: “we show that the dropout regularizer is first-order equivalent to an L2 regularizer applied after scaling the features by an estimate of the inverse diagonal Fisher information matrix”.
4.3.5 Theme of noise in forward pass
Dropout属于一类更一般性的方法,这种方法的基本特征是给神经网络的前向处理引入随机行为(stochastic behavior)。During testing, the noise is marginalized over *analytically* (as is the case with dropout when multiplying by ), or *numerically* (e.g. via sampling, by performing several forward passes with different random decisions and then averaging over them). An example of other research in this direction includes DropConnect, where a random set of weights is instead set to zero during forward pass. As foreshadowing(伏笔,铺垫), Convolutional Neural Networks also take advantage of this theme with methods such as stochastic pooling, fractional pooling, and data augmentation. We will go into details of these methods later.
4.3.6 Bias regularization
正如在线性分类一节中提到过的,通常不会对偏置(bias)参数进行正则化处理,因为它们并不与数据发生乘性相互作用,and therefore do not have the interpretation of controlling the influence of a data dimension on the final objective(?不知所云?)。然后,在实践中,针对偏置实施正则化(辅以适当的数据预处理)也没有导致显著的性能损失。这可能是因为偏置参数个数远远小于权重参数个数。
4.3.7 Per-layer regularization
不同层采用不同方法不同强度的正则化的做法不是很常见(或许输出层是个例外)。很少有公开发表的文献涉及关于这个idea。
4.3.8 小结
In practice:
当前最常用的做法是采用单一的全局性的L2正则化,其中正则化强度用交叉验证的方式去进行优化。 然后,再结合针对每一层施加Dropout。参数p=0.5是一个合理的缺省选择,但是也同样可以通过交叉验证进行优化。
5. Loss function
在前面讨论正则化时其实已经讨论了损失函数(loss function,也称目标函数,objective function)的一部分,正则化损失可以看作是对于模型复杂度的一种惩罚措施。损失函数的另一个部分其实也更基本的部分是所谓的数据损失(data loss),在监督学习中,data loss是用于衡量预测结果(e.g. the class scores in classification)与真值(groung truth)之间的契合度(compatibility, 契合度越大则data loss越小)。总的data loss是每个数据样本的data loss的平均,如下所示,其中N表示训练集合的样本数:

假定神经网络输出层激励函数简化地表示为:。在实际应用中可能会碰到以下几类问题,以下分别讨论。
5.1 classification, 分类
假定有一个数据集,对于每个样本有唯一的正确标签。最常见的代价函数之一是SVM loss(e.g. the Weston Watkins formulation):

当然,也有研究者报告说采用平方合页损失(squared hinge loss, 即: )能取得更好的性能。
另一种常见的data loss则是在所谓的Softmax classifier中采用的交叉熵损失(cross entropy loss):

Problem: Large number of classes.
当分类数非常大时(比如说ImageNet有22,000中类别), 计算完整的softmax probabilities代价昂贵。在一些特定应用中,通常采用一些近似的方法。比如说,在自然语言处理中,通常使用所谓的 *Hierarchical Softmax。*
5.2 Attribute classification
5.3 Regression
5.4 Structured prediction
6. Summary
通常推荐的数据预处理包括:零均值化,归一化(both are along each feature)
权重参数初始化推荐方式:
w = np.random.randn(n) * sqrt(2.0/n).正则化:L2 regularization and dropout (the inverted version)
Use batch normalization
损失函数:SVM loss;softmax loss;...
至此,我们讨论了如何进行数据预处理,以及建立和初始化模型,接下来将讨论学习过程以及它的动力学机制(dynamics).
版权归原作者 笨牛慢耕 所有, 如有侵权,请联系我们删除。