线性代数（四）| 解方程 齐次性 非齐次性 扩充问题

文章目录

系数矩阵 增广矩阵

      A 
     
     
     
       m 
      
     
       × 
      
     
       n 
      
     
    
   
     X 
    
   
     = 
    
   
     B 
    
   
  
    A_{m×n}X=B 
   
  
Am×n​X=B

1 方程解的个数

m 代表有m个方程 n代表有n个未知数

系数矩阵的秩与增广矩阵的秩不同 无解

若相同 ，如系数矩阵的秩和未知数个数n相同，则有唯一解，若系数矩阵的秩小于未知数个数n，则有无穷多解

2 解方程步骤

2.1 齐次性方程组

（1） 写出系数矩阵

（2）初等变换到行简化阶梯矩阵

（3）写出同解方程组

（4）赋值写出基础解系

例题：求解方程组

2.2 非齐次方程组

齐次性方程组的通解加上非齐次性方程组的一个特解

（1） 写出增广矩阵

（2）初等行变换到行简化阶梯矩阵

（3）写出同解方程组代入特值求出一个特解

（4）去掉常量代入特值求得齐次性方程组的通解

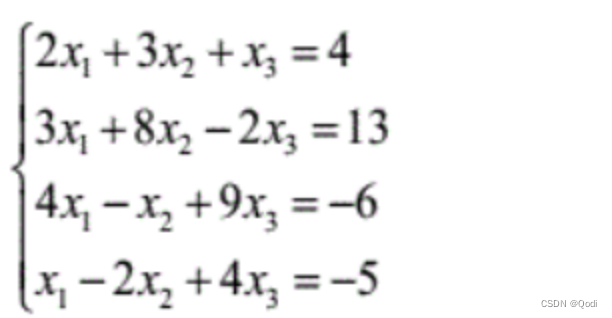
3 一些扩充问题

1、线性无关线性相关相结合的知识点

求齐次性方程组的通解加上一个非齐次性方程组的一个特解