Python实验--手写KNN+PCA实现药品聚类和手写字识别

1. KNN

算法原理：

1. 从D中随机取k个元素，作为k个簇的各自的中心；
2. 分别计算剩下的元素到k个簇中心的相异度，将这些元素分别划归到相异度最低的簇；
3. 根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均数。
4. 将D中全部元素按照新的中心重新聚类。
5. 重复第4步，直到聚类结果不再变化。
6. 将结果输出 # 计算到中心的欧氏距离def Distance(train, center, k): dist1 = [] for data in train: diff = np.tile(data, (k,1)) - center squaredDiff = diff ** 2 squaredDist = np.sum(squaredDiff, axis=1) distance = squaredDist ** 0.5 dist1.append(distance) dist = np.array(dist1) return dist# 集群分配def classify(train, center, k): dist = Distance(train, center, k) # 计算距离原中心的距离 minDistIndices = np.argmin(dist, axis=1) # 分簇 newcenter = pd.DataFrame(train).groupby(minDistIndices).mean() # 计算簇中所有元素的算数平均值 newcenter = newcenter.values # 更新中心 changed = newcenter - center return changed, newcenterdef kmeans(train, k): center = random.sample(train, k) print('center：%s' % center) col = ['black', 'black', 'blue', 'blue'] for i in range(len(train)): plt.scatter(train[i][0], train[i][1], marker='o', color=col[i], s=40, label='origin') for j in range(len(center)): plt.scatter(center[j][0], center[j][1], marker='x', color='red', s=50, label='center') plt.show() changed, newcenter = classify(train, center, k) while np.any(changed != 0): # 直到中心不变化 changed, newcenter = classify(train, newcenter, k) center = sorted(newcenter.tolist()) classes = [] dist = Distance(train, center, k) minDistIndices = np.argmin(dist, axis=1) for i in range(k): classes.append([]) for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素 classes[j].append(train[i]) return center, classes

2. PCA

主成分分析主要功能是以精度换速度，减少属性个数，提高算法运算速度

选择属性指标为每个指标对整体方差和的贡献率

计算原理：

1.去中心化

2.计算协方差矩阵

3.求解特征值和特征值向量

4.对特征值从大到小排序，选择最大的k个，然后将其对应的特征向量组成特征向量矩阵

5.反变换到原先向量空间

def pca(data, n_dim):

    data = data - np.mean(data, axis=0, keepdims=True)
    XTX = np.dot(data.T, data) 
    eig_values, eig_vector = np.linalg.eig(XTX)   #特征值 特征向量
    indexs_ = np.argsort(-eig_values)[:n_dim]
    picked_eig_vector = eig_vector[:, indexs_]
    
    
    data_ndim = np.dot(data, picked_eig_vector) #坐标表示
    return data_ndim, picked_eig_vector

3. 药品数据测试

数据为[(1, 1), (2, 2), (4, 3), (5, 4)]

要求分成两类

train =  [(1, 1),(2, 2),(4, 3),(5,4)]
    center, classes = kmeans(train, 2)
    print('center：%s' % center)
    print('classes：%s' % classes)
    col = ['black', 'black', 'blue', 'blue']
    for i in range(len(train)):
        plt.scatter(train[i][0], train[i][1], marker='o', color=col[i], s=40, label='row')
        for j in range(len(center)):
            plt.scatter(center[j][0], center[j][1], marker='x', color='red', s=50, label='center')
    plt.show()

结果：

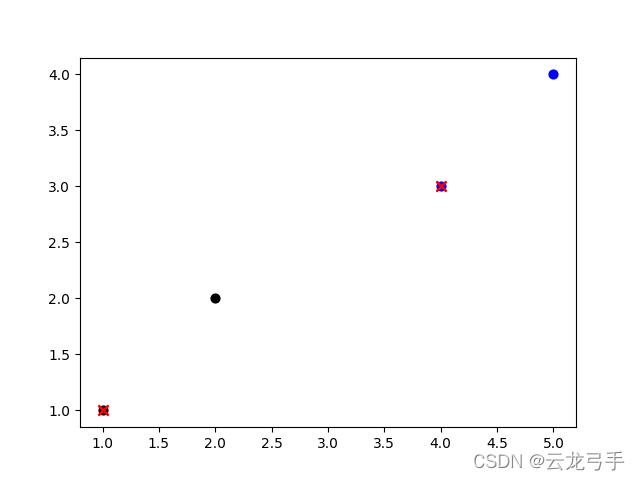
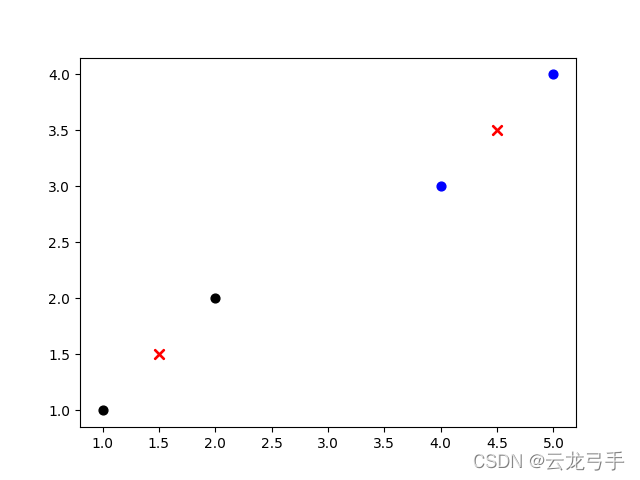
4. 手写字识别

数据集采用sklearn自带的digits数据集，包含0-9是个数字共1797个样本，每个样本为8*8的灰度图

要求一：利用sklearn实现PCA+KNN

data = load_digits().data
    labels = load_digits().target
    pca = PCA(n_components=15)
    data_new = pca.fit_transform(data)
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(data_new, labels, test_size=0.3, random_state=10)

    clf = KNeighborsClassifier(n_neighbors=3, weights='uniform',
                               algorithm='auto', leaf_size=30,
                               p=2, metric='minkowski', metric_params=None,
                               n_jobs=None, )
    # train
    clf.fit(Xtrain, Ytrain)
    print(clf.score(Xtest, Ytest))

其中pca的保留属性数量选择15，总共的方差贡献率已超过98%

结果：

0.9833333333333333

要求二：实现手写PCA+KNN

# KNN.py
def knn(train, label, k):
    n = len(train)
    classes = zeros(n)
    center = random.sample(train, k)

    changed, newcenter = classify(train, center, k)
    while np.any(changed != 0):
        changed, newcenter = classify(train, newcenter, k)

    center = sorted(newcenter.tolist())

    dist = Distance(train, center, k)  # 调用欧拉距离
    minDistIndices = np.argmin(dist, axis=1)
    for i, j in enumerate(minDistIndices):
        classes[i] = j # 每个值对应的类序号
    dic = {0:0, 1:0, 2:0, 3:0, 4:0, 5:0, 6:0, 7:0, 8:0, 9:0} # 类序号对应的标签
    vote = []
    for i in range(k):
        vote.append(zeros(k))
    for i in classes:
        vote[classes[i]][label[i]] += 1  # 统计每个类中每个标签的数量
    for i in range(k):
        index = vote[i].index(max(vote[i]))
        dic[i] = index  # 以每个类中最多的标签作为当前类对应的标签
    n_wrong = 0
    for i in classes:
        if label[i] != dic[classes[i]]:
            n_wrong += 1  # 统计分类错误

    acc = 1 - n_wrong/n
    return acc  # 返回acc

# PCA.py
def PCA_KNN_hand():
    data = load_digits().data
    print(data.shape)
    labels = load_digits().target
    data_15d, picked_eig_vector = pca(data, 15)
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(data_15d, labels, test_size=0.3, random_state=10)

    acc = KNN.knn(list(Xtrain), list(Ytrain), 10)
    print(acc)

    其中重写了knn函数（KNN.py中），是因为原先的knn函数只实现了聚类，但是对于每个类别的标签没有涉及。这里采用投票制，将每个类中每中标签的个数统计之后，以票数最高的标签作为当前类别的标签值

结果：

0.9124900556881463