通信原理循环码基本原理

一、码多项式

一个长度为 $\large n$ 的码组 $\large A=(a_{n-1},a_{n-2},...,a_0)$ 可表示成如下多项式形式：

$\large A(x)=a_{n-1} x^{n-1}+a_{n-2} x^{n-2}+\cdots+a_{1} x+a_{0}$

多项式的系数就是码组中的各码元， $\large x$ 仅是码元位置标记。

n=7 时： $\large A(x)=a_{6} x^{6}+a_{5} x^{5}+a_{4} x^{4}+a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0}$

例：码字（1100101）的多项式可表示为：

$\large \begin{aligned} A(x) & =1 \cdot x^{6}+1 \cdot x^{5}+0 \cdot x^{4}+0 \cdot x^{3}+1 \cdot x^{2}+0 \cdot x+1 \\ & =x^{6}+x^{5}+x^{2}+1 \end{aligned}$

二、码多项式的按模运算

一般来说，若一个整数 $\large m$ 可以表示为

$\large \frac{m}{n}=Q+\frac{p}{n}, \quad p<n$ ， $\large Q$ 为整数

则在模 $\large n$ 运算下，有

$\large m \equiv p\quad mod\quad n$

即在模 $\large n$ 运算下，一个整数 $\large m$ 等于它被 $\large n$ 除得到的余数。

对于任意多项式 $\large F(x)$ 被一 $\large n$ 次多项式 $\large N(x)$ 除，得到商式 $\large Q(x)$ 和一个小于 $\large n$ 次的余式 $\large R(x)$ ,即

$\large \frac{F(x)}{N(x)}=Q(x)+\frac{R(x)}{N(x)} \text { or } F(x)=N(x) Q(x)+R(x)$

则

$\large F(x)\equiv R(x) \quad mod \quad N(x)$

三、循环码的码多项式

在循环码中，若 $\large A(x)$ 是一个长为 $\large n$ 的许用码组，则 $\large x^i\cdot A(x)$ 在按模 $\large x^n+1$ 运算下，也是该编码中的一个需用码组，即若

$\large x^{i} \cdot A(x) \equiv A^{\prime}(x) (mod \left.\left(x^{n}+1\right)\right)$

则 $\large A^{\prime}(x)$ 也是该编码中的一个需用码组，这是因为 $\large A^{\prime}(x)$ 正是 $\large A(x)$ 代表码组向左循环移位 $\large i$ 次的结果。

四、循环码的生成矩阵

在 $\large (n,k)$ 循环码的 $\large 2^k$ 个码组中挑出一个前面 $\large (k-1)$ 位都是“0”的码组用 $\large g(x)$ 表示：

根据循环性， $\large g(x)$ ， $\large xg(x)$ ， $\large \large x^2g(x)$ ，...， $\large x^{k-1}g(x)$ 都是该循环码组的码组，且都线性无关。

因此，可以用这 $\large k$ 个线性无关的码组可构成该循环码的生成矩阵 $\large G$ ，即

$\large G\left ( x \right ) =\left[\begin{array}{c} x^{k-1} g(x) \\ x^{k-2} g(x) \\ \vdots \\ x g(x) \\ g(x) \end{array}\right]$

$\large g(x)$ 是循环码的核心。对于给定的 $\large k$ 位信息码，由 $\large g(x)$ 构造出 $\large G(x)$ ，从而产生 $\large (n,k)$ 循环码。

$\large g(x)$ 称为循环码的生成多项式，一旦确定了 $\large g(x)$ ，则整个 $\large (n,k)$ 循环码就被确定了。 $\large g(x)$ 是 $\large (n,k)$ 循环码中唯一的常数项不为0的 $\large (n-k)$ 次多项式。

例：

已知一种 $\large (7,3)$ 循环码的全部码组为：

$\large \begin{array}{llll} 0000000 & 0101110 & 1001011 & 1100101 \\ 0010111 & 0111001 & 1011100 & 1110010 \end{array}$

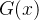
试求：（1）该循环码的生成多项式 $\large g(x)$

       （2）生成矩阵![\large G(x)](https://latex.csdn.net/eq?%5Clarge%20G%28x%29)

码组是：0010111，码组中唯一一个4次多项式 $\large g(x)=x^{4}+x^{2}+x+1$

$\large G(x)=\begin{bmatrix} x^2g(x)\\ xg(x)\\ g(x) \end{bmatrix}= \left[\begin{array}{l} x^{6}+x^{4}+x^{3}+x^{2} \\ x^{5}+x^{3}+x^{2}+x \\ x^{4}+x^{2}+x+1 \end{array}\right]$ 或者 $\large \boldsymbol{G}=\left[\begin{array}{c} \mathbf{1 0 1 1 1 0 0} \\ \mathbf{0 1 0 1 1 1 0} \\ \mathbf{0 0 1 0 1 1 1} \end{array}\right]$

$\large \begin{aligned} A(x)&=[a_6a_5a_4]G(x)=[a_6a_5a_4] \left[ \begin{array}{c} x^2g(x)\\ xg(x)\\ g(x) \end{array} \right]\\ & =a_{6} x^{2} g(x)+a_{5} x g(x)+a_{4} g(x) \\ & =\left(a_{6} x^{2}+a_{5} x+a_{4}\right) g(x) \end{aligned}$

所有码多项式 $\large A(x)$ 都可被 $\large g(x)$ 整除，而且任意一个次数不大于 $\large (k-1)$ 的多项式乘 $\large g(x)$ 都是码多项式。

换言之，任一循环码多项式 $\large A(x)$ 都是的倍式。

五、如何寻求任一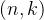 $\large (n,k)$ 循环码循环码的生成多项式 $\large g(x)$

$\large \because$ 任一循环码多项式 $\large A(x)$ 都是 $\large g(x)$ 的倍式。

$\large \therefore$ $\large g(x)$ 本身也是一个码组，即有 $\large A^\prime(x)=g(x)$

$\large \because$ 码组 $\large A^\prime(x)$ 是一个 $\large (n-k)$ 次多项式，故 $\large x^k\large A^\prime(x)$ 是一个 $\large n$ 次多项式。 $\large x^k\large A^\prime(x)$ 在模 $\large x^n+1$

运算下也是一个码组，故可以写作

$\large \frac{x^{k} A^{\prime}(x)}{x^{n}+\mathbf{1}}=Q(x)+\frac{A(x)}{x^{n}+\mathbf{1}}$

上式左端分子和分母都是n次多项式，故商式 $\large Q(x) = 1$ 上式可化成

$x^{k} A^{\prime}(x)=\left(x^{n}+\mathbf{1}\right)+A(x)$

将 $\large A^{\prime}(x)=g(x)$ 和 $\large A(x)=h(x)\cdot g(x)$ 代入，化简后可以得到

$\large x^{n}+1=g(x)\left[x^{k}-h(x)\right]$

这表明：循环码的生成多项式** $\large g(x)$ 应该是 $\large (x^n+1)$ 的一个 $\large (n-k)$ **次因子。

六、循环码的监督矩阵和监督多项式

1、监督多项式

由于生成多项式** $\large g(x)$ 能除尽 $\large (x^n+1)$ **，可以表示为

$\large g(x)=g_{n-k} x^{n-k}+\cdots+g_{1} x+g_{0}$

且 $\large g_0=1$ ,因此

$\large x^{n}+1=g(x) h(x)$

因为 ** ** $\large g(x)$ 是 $\large (x^n+1)$ 的一个 $\large (n-k)$ 次因子，则以 $\large g(x)$ *为生成多项式，则生成一个 $\large (n,k)$ 循环码；而以 $\large h(x)$ 为生成多项式，则生成一个 $\large (n,n-k)$ 循环码，这两个循环码互为对偶码。*

由于上式是循环码必须满足的监督关系，因此许用码组 $\large h(x)$ 称为监督多项式，不妨令

$\large h(x)=h_{k} x^{k}+\cdots+h_{1} x+h_{0}$

由监督关系可以知道

$\large \begin{array}{l} g_{n-k} \cdot h_{k}=1 \\ g_{0} \cdot h_{0}=1 \\ g_{1} \cdot h_{0}+g_{0} \cdot h_{1}=0 \\ g_{2} \cdot h_{0}+g_{1} \cdot h_{1}+g_{0} \cdot h_{2}=0 \\ \cdots \\ g_{n-1} \cdot h_{0}+g_{n-2} \cdot h_{1}+\cdots+g_{n-k} \cdot h_{k-1}+\cdots+g_{0} \cdot h_{n-1}=0 \end{array}$

因此可以由生成多项式确定监督多项式的系数。

2、监督矩阵

监督多项式 $\large h(x)=h_{k} x^{k}+\cdots+h_{1} x+h_{0}$ ，设 $\large h^{*}(x)$ 是 $\large h(x)$ 逆多项式，则

$\large h^{*}(x)=h_{0} x^{k}+h_{1} x^{k-1}+\cdots+h_{k-1} x+h_{k }$

因为 $\large \boldsymbol{G} \boldsymbol{H}^{\mathrm{T}}=0, r=n-k$ 。则监督矩阵 $\large \boldsymbol{H}_{r \times n}$ 完全可由监督多项式 $\large h(x)$ 的系数确定，由此可得循环码的监督矩阵为

$\large \boldsymbol{H}_{r \times n}=\left[\begin{array}{c} x^{n-k-1} \cdot h^{*}(x) \\ x^{n-k-2} \cdot h^{*}(x) \\ \vdots \\ x \cdot h^{*}(x) \\ h^{*}(x) \end{array}\right]$

$\large =\left[\begin{array}{ccccccccccc} h_{0} & h_{1} & \cdots & h_{k-1} & h_{k} & 0 & 0 & \cdots & & & 0 \\ 0 & h_{0} & h_{1} & \cdots & h_{k-1} & h_{k} & 0 & 0 & \cdots & & 0 \\ 0 & 0 & h_{0} & h_{1} & \cdots & h_{k-1} & h_{k} & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & & & & & & & & & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & h_{0} & h_{1} & \cdots & h_{k-1} & h_{k} \end{array}\right]$

上述的监督矩阵不是典型的，可将它经线性变化成典型形式，即典型的监督矩阵为

$\large \boldsymbol{H}_{r \times n}=\left[\boldsymbol{P} \vdots \boldsymbol{I}_{r}\right]$

标签：算法人工智能

本文转载自: https://blog.csdn.net/m0_51143578/article/details/128398749
版权归原作者 WHS-_-2022 所有，如有侵权，请联系我们删除。