碎纸片的拼接复原-基于边缘匹配思想

目录

选题

题目背景

破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。传统上，拼接复原工作需由人工完成，准确率较高，但效率很低。特别是当碎片数量巨大，人工拼接很难在短时间内完成任务。随着计算机技术的发展，人们试图开发碎纸片的自动拼接技术，以提高拼接复原效率。

问题提出

对于给定的来自同一页印刷文字文件的碎纸机破碎纸片（仅纵切），建立碎纸片拼接复原模型和算法，并针对附件1 一页文件的碎片数据进行拼接复原。如果复原过程需要人工干预，请写出干预方式及干预的时间节点。复原结果以图片形式及表格形式表达（见【结果表达格式说明】）。

问题分析

我针对仅纵切的情况，首先将其图像进行数字化处理，并将其二
值化，分别得到图像的左右边缘用于计算边缘匹配度，其次，根据其图像左边距特征确定左边第一碎片，并基于边缘匹配度的贪心策略得到从左至右复原的结果。结果表明，我的方法对于中文情况适用性较好。

文献查找

1. 王昕.基于图像处理的文档碎纸拼接技术研究【Z】.大学教育,2015(08):133-134.
2. 刘威,王军民,刘克勤.基于边缘匹配的纵向碎纸拼接方法【J】.计算机与现代化,2019(02):55-59.
3. 刘铁.基于数字图像的碎纸复原模型与算法——2013年全国大学生数学建模B题碎纸片的拼接复原问题【J】.重庆理工大学学报(自然科学),2015(03):83-88.
4. 刘亚威,王军民,刘威.基于相关矩阵的纵向碎纸拼接方法【J】.计算机与现代化,2019(10):43-47.

    *本文基于文献2进行阐述

建立数学模型

基本假设：

假设 1.附件中所给的碎纸图片无噪声，即不缺少，不增多。

假设 2.碎纸图片可进行图像数字化处理以及二值化处理，可以直接提取图像左右边界特征。

假设 3.附件中的每一张碎纸的大小统一，图片内容清晰可见。

名词解释和符号说明：
符号说明i,j图片序数left图片左边界矩阵right图片右边界矩阵D图片横向二值化后首列矩阵S相似度矩阵A均值Dk标准偏差N匹配度矩阵Label顺序列表c具有左边距特征的碎纸图片

方法选取的数学思想：

• 边缘匹配
• 相关度分析
• 贪婪策略

建模过程

1. 用 PIL 包下的 Image 函数读取附件 1 中的碎片图片并统一其大小为 2004 行 68 列，并用矩阵存放。
2. 提取每个图片左右边界的灰度值，并将其二值化，左边界保存在 left中，其大小为 2004 行 20 列，同理，将右边界保存在 right 中，大小与 left 同等。
3. 求匹配度矩阵 n，具体做法为依次求 left 第 i 列 left[: , i]与 right 第 j 列right[: , j] 之间的匹配度，存放在匹配矩阵 n 中，其中 ni,j 表示第 i 张碎片的左边缘与第 j 张碎片的右边缘的匹配度，由于自身无法与自身匹配，所以将其置为 0，即当 i=j时。
4. 求相似度矩阵 S 然后求取纸片之间的相似度，保存为相似度矩阵 S。依次求矩阵 D 中第 i 列 Di(i=1，2，…，19)与剩余 18 列 Dj(j≠i，j=1，2，…，19)的相似度，比较 Di 与 Dj 行元素相同的总行数，即为二者的相似度，结果保存为 Sij
5. 建立顺序列表 label 用于记录排序顺序，以 c 作为首张，寻找匹配度矩阵 n[: , c]中最大匹配值，将其最大匹配值的行为设定为 r，之后求相似度矩阵 S[: , c]中非 0 所有元素的均值 A 与标准偏差 Dk。 当满足𝑆r,c < 𝐴 + 0.5𝐷k时，则表示 r 不符合条件，将 n[r,c]置为 0 防止重复查找，重新查找匹配矩阵 n[:,c]中的最大匹配值； 当满足𝑆r,c ≥ 𝐴 + 0.5Dk时，则表示 r 为 c 的下一碎片序号，将 r 添加至 label 中，并将 n[c, :]与 S[: , c]置为 0，防止重复查找，同时设置 c =r 进行下一轮查找，直到所有碎片都已经进入 label。
6. 利用 numpy.hstack()函数将 label 中序号所对应的图片进行矩阵合并，再通过 Image.fromarray()函数将其转化为图片，达到还原的目的。 具体流程图如图表所示。

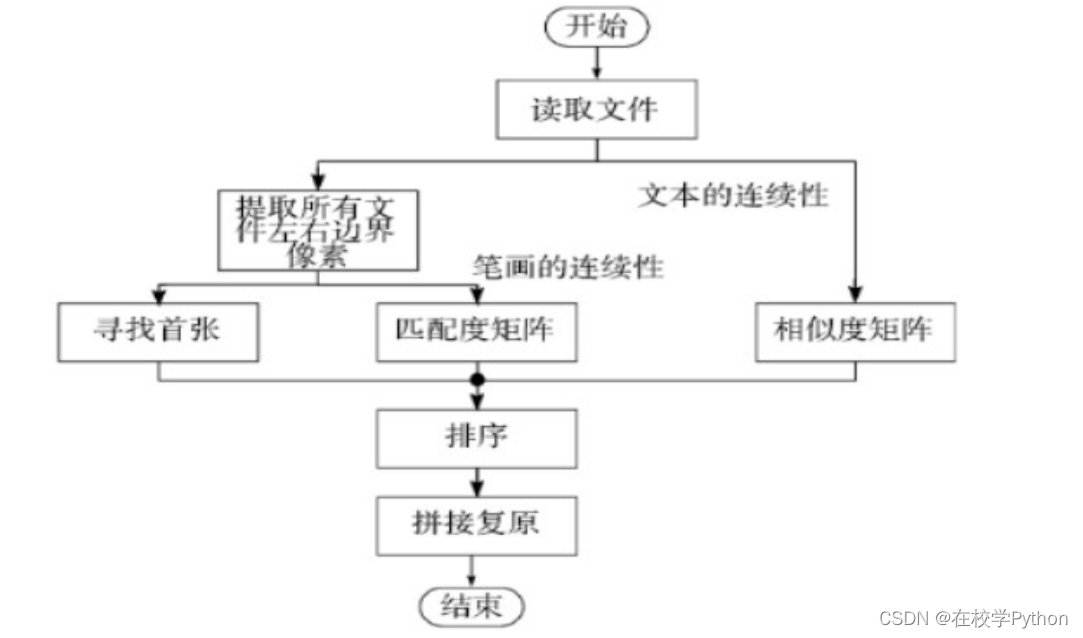
注：流程图来源于文献2

工具选择与应用

• PyCharm
• NumPy
• PIL.Image

代码实现

from PIL import Image

import numpy as np

np.set_printoptions(threshold=np.inf)# 完整打印，便于调试
imglst =[]defcalculate_matching(left,right,rc =2004):
    r =0for x inrange(rc):if x ==0:if right[x]== left[x]or right[x]== left[x+1]:
                r+=1elif x == rc-1:if right[x]== left[x]or right[x]== left[x-1]:
                r+=1else:if right[x]== left[x]or right[x]== left[x-1]or right[x]== left[x+1]:
                r+=1else:return r

defcalculate_Similarity(Di,Dj,rc =2004):
    count =0for i inrange(rc):if Di[i]== Dj[i]:
            count +=1else:return count

defraw_binary(src:str):
    im = Image.open(src)
    im_array = np.array(im)
    r,c = im_array.shape

    for i inrange(r):
        flag =Falsefor j inrange(c):if im_array[i,j]!=255:
                flag =Truebreakif flag:
            im_array[i,:]=1else:
            im_array[i,:]=0return im_array

defmaxMatching(matrix):
    r,= np.unravel_index(np.argmax(matrix),matrix.shape)#返回最大值下标return r
#计算均值与标准偏差defcal_AandDk(matrix):
    lst =[]for item in matrix:if item !=0:
            lst.append(item)else:
        matrix = np.array(lst)
    l =len(matrix)
    A = np.sum(matrix)/l
    Dk =(sum(map(lambda  e:(e-A)*(e-A),matrix))/l)**0.5return A,Dk

'''
读取图片
'''defreadImg(src:str,height=2004,width=68):
    im = Image.open(src).resize((width,height),Image.ANTIALIAS)

    imglst.append(np.array(im))return np.where(np.array(im)==255,0,1)defreducateImg(label:list):#图片拼接
    newImg =imglst[label[0]]for i inrange(1,len(label)):
        newImg = np.hstack((newImg,imglst[label[i]]))
    out = Image.fromarray(newImg)
    out.save(r'C:\Users\anonymous\Desktop\1.png')defmain():'''
    question1图片：
        height:2004
        width:68/69
        count:20

    :return:
    '''
    src ='image1/{}.png'# 图片路径'''
        初始化left与right
    '''
    c =0# 拼接顺序
    left = np.zeros((2004,20), dtype='int8')# 经过观察，行数为2004
    right = left.copy()
    D = left.copy()for i inrange(1,21):if i <10:
            image = readImg(src.format('0'+str(i)))
            raw_binary_img = raw_binary(src.format('0'+str(i)))else:
            image = readImg(src.format(i))
            raw_binary_img = raw_binary(src.format(i))

        left[:, i -1]= image[:,0]
        right[:, i -1]= image[:,-1]
        D[:,i-1]= raw_binary_img[:,0]

    margin_index =list(np.any(left, axis=0)).index(False)
    c = margin_index

    n = np.zeros((20,20),dtype=int)
    S = n.copy()#计算匹配度与相似度for i inrange(20):for j inrange(20):if i == j:
                n[i][j]=0
                S[i][j]=0else:
                n[i][j]= calculate_matching(left[:,i],right[:,j])
                S[i][j]= calculate_Similarity(D[:,i],D[:,j])

    A =0#均值
    Dk =0#标准偏差
    label =[0]# 20张碎片whileTrue:
        label[-1]= c
        r = maxMatching(matrix=n[:, c])
        A,Dk = cal_AandDk(S[:,c])if S[r,c]<A+0.5*Dk:

            n[r,c]=0
            r =0else:
            label.append(r)
            n[c,:]=0
            S[:,c]=0
            c = r
        iflen(label)==20:break

    reducateImg(label)print(label)if __name__ =='__main__':
    main()

结果

附件

• 碎纸附件：

https://pan.baidu.com/s/1FEeCB27SZig3IBV4f23K7w?pwd=1630