排序 ---数据结构

本节内容讲述关于各种排序！

文章目录

插入排序

基本的描述！就是从一个数组之中插入一个数字不断的插入数字，使的其有序。具体的描述看插入排序。基本的思想就是从小变成大的数量，然后得出结果。

voidInsertSort(int*a,int n){for(int end =0; end < n -1; end ++){int tmp = a[end +1];while(end >=0){if(a[end]> tmp){
                a[end +1]= a[end];
                end--;}elsebreak;}
        a[end +1]= tmp;}}

时间复杂度为O（N^ 2），完全与应该的顺序相反！最好为O（N），完全有序。

希尔排序

通过建立gap的大小的数组来实现分组数组然后分别进行插入排序！:希尔排序的动图演示

最开始的时候是进行先分组安装gap的距离进行分组。进行插入排序。然后不断减小gap的值最后可以得到gap == 1，的时候完全就是插入排序。

voidShellSort(int*a,int n){int gap = n;while(gap >1){

        gap = gap/3+1;for(int m =0; m < gap; m++){for(int i = m; i < n - gap; i += gap){//单层插入int end = i;int tmp = a[end + gap];while(end >=0){if(tmp > a[end]){break;}else{
                        a[end + gap]= a[end];
                        end -= gap;}}
                a[end + gap]= tmp;}}}}}

通过大量的计算知道，gap/3平均复杂度最小O（Nlog3N）。

时间复杂度分析

开始时，gap非常大最里面的那一层排序时间复杂度为O（n）。
```（假设gap等于二分之一的数组长度。比较的时间复杂度O（n^(1/2)。
交换的时间复杂度同上）。gap足够小的时候，数组最近有序，
所以时间复杂度为O（n）。

所以说内部的时间复杂度相同，取决于gap = gap /c  + b之中c的值
（b的目的决定了最后会发生gap == 1的情况）！

选择排序

选择排序的动图
通过简单的进行大小的比较，直接选取大的放在左边或者右边。然后重新选择第二小的或者是第二大的东西。
下面进行数据优化的，同时筛选最大的和最小的数据，左边为最小的，右边为最大值。重复上述过程！

voidSelectSort(int*a,int n){int max = n -1;int min =0;int tmp =0;for(int i =0; i < n; i++){
        
        tmp = i;while(tmp < n - i){//单次循环if(a[tmp]> a[max]){Swap(&a[tmp],&a[max]);}if(a[tmp]< a[min]){Swap(&a[tmp],&a[min]);}
            tmp++;}
        min++;
        max--;}}

快速排序

一共有3种的使用方法！

hora版本（最基本）

hora版本动图

基本的思想，分治，让大问题变成小问题，每一个中间使用一个key进行隔离。

选择一个keyi，然后选取两个指针。一个为头指针，一个为尾指针。
一般keyi为头指针大于keyi一个位置信息。然后尾指针先动，

如果比keyi的值大向左边移动，并且重复上述过程，如果小于keyi的值，该指针就不会发生移动,
最后面两者相遇的位置肯定小于keyi的具体方的值。因为右边先移动的原因！如果不知道，可以进行画图了解。不同的升序降序需要改变移动的开始位置信息！

代码：

voidSwap(int*a,int*b){int tmp =*a;*a =*b;*b = tmp;}intPartSort1(int*a,int left,int right){int keyi = left;while(left < right){while(a[right]>= a[keyi]&& left < right){
            right--;}while(a[left]<= a[keyi]&& left < right){
            left++;}Swap(&a[right],& a[left]);}Swap(&a[right],&a[keyi]);return left;}voidQuickSort1(int*a,int begin,int end){//Hora排序if(begin >= end){return;}int keyi =PartSort1(a, begin, end);QuickSort1(a,begin,keyi -1);QuickSort1(a, keyi +1, end);}

挖坑法

通过最开始的keyi作为一个坑位（选择左边），先进行右边（left）比较。如果大于keyi话，继续向左，移动一个坑位。小于与keyi交换数据。
然后（right）进行移动。如果找到与之前数据大的进行交换。
最终right与left相遇,该位置更新坑位变成了最开始的keyi的数字！然后进行递归（keyi把这个数组分成了为两个部分）,继续进行上述过程，分区域进行分割，每一个区域继续上诉过程！

intPartSort(int*a,int left,int right){int keyi = a[left];int pit = left;while(left < right){while(a[right]>= keyi && left < right){
            right--;}
        a[pit]= a[right];
        pit = right;while(a[left]<= keyi && left < right){
            left++;}
        a[pit]= a[left];
        pit = left;}
    a[pit]= keyi;return pit;}voidQuickSort(int*a,int begin,int end){if(begin >= end){return;}int keyi =PartSort(a,begin, end);QuickSort(a, begin, keyi -1);QuickSort(a, keyi +1, end);}

前后指针法

通过cur和prev两个指针，进行排序。cur找到小的位置(比keyi小的位置)， prev++，然后交换prev和位置的具体值。然后进行进行相关内容继续进行，直到结束相应的结果！单次循环完成了！进行进行分治的方法（递归实行）！

intPartSort3(int*a,int left,int right){int keyi = left;int prev = left;int cur = left +1;while(cur <= right){if(a[cur]<  a[keyi]&& a[++prev]!= a[cur]){Swap(&a[cur],&a[prev]);}
        cur++;}Swap(&a[prev],&a[keyi]);return prev;}voidQuickSort3(int*a,int begin,int end){if(begin >= end){return;}int keyi =PartSort3(a,begin, end);QuickSort3(a, begin, keyi -1);QuickSort3(a, keyi +1, end);}

时间复杂度

时间复杂度的计算：首先这里面使用的是分治的方法及二分法。
最好的情况选择keyi为排序完之后的数字之中的中间的数字。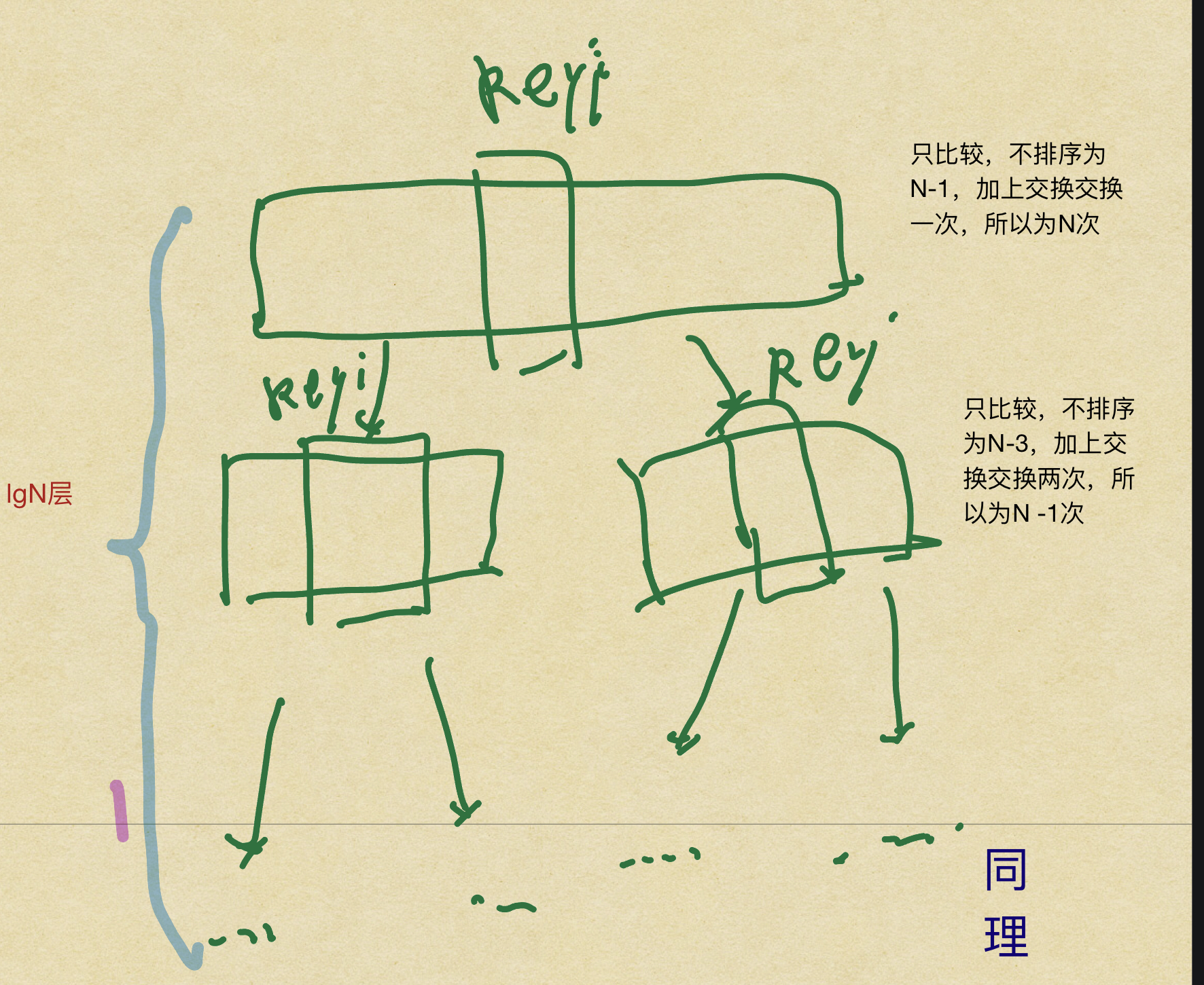

一共大概有lgN层，每一层大概为N次比较所有为O（NlgN）。
最坏情况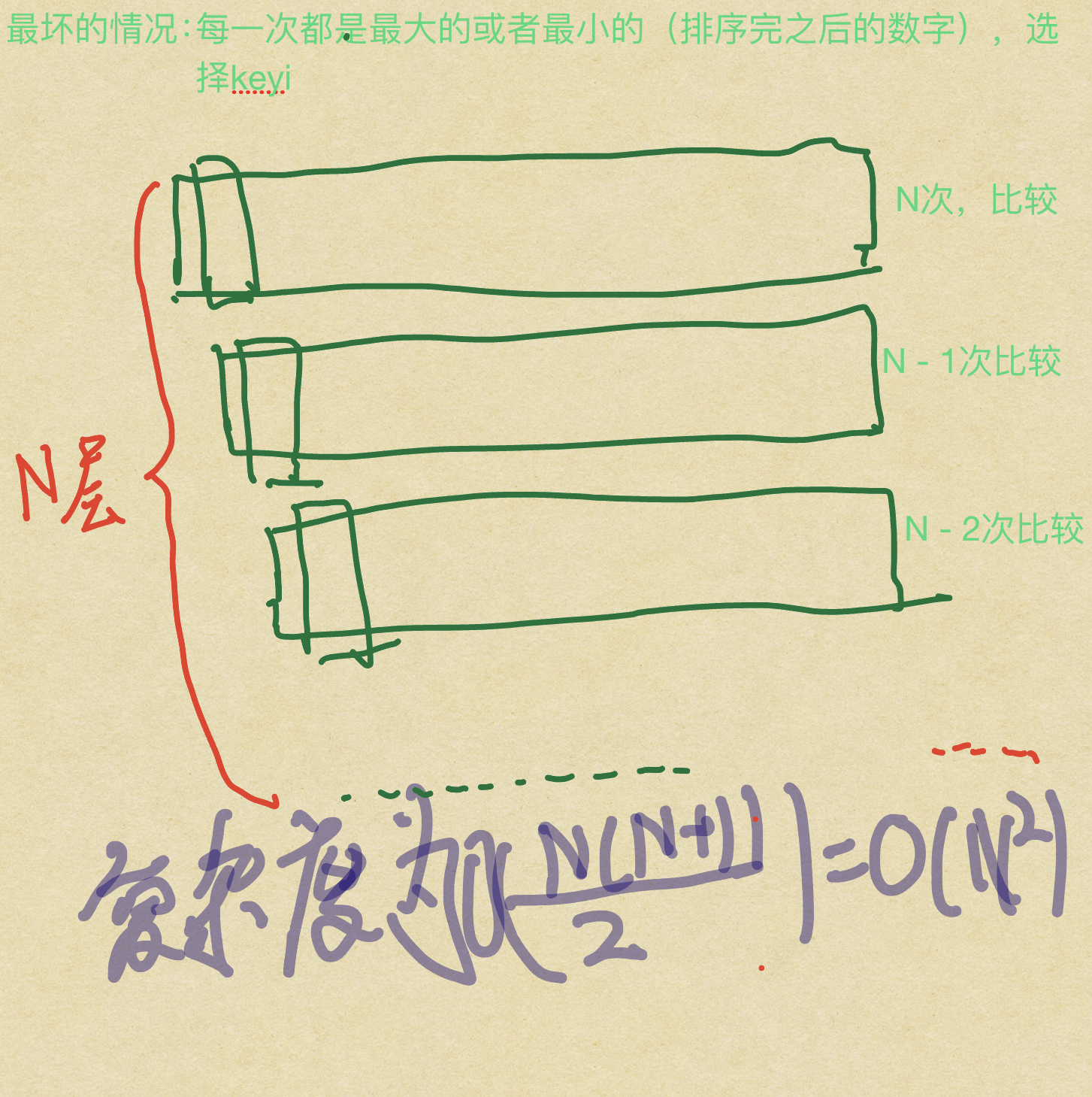

数据优化

对于keyi的选择可以更加的优化，可以更好进行排序数据的优化！一般进行头，首，中数字，的 数组中间的作为keyi。进行数据选取优化。

—————————————————————————————————————————————————————————————————————————

通过结构实现

通过队列和栈进行数组的分割！代替递归分割的作用！基本思想相同。

并归排序

数据量大，没有办法储存到内存条之中！进行数组分割，然后数组，进行继续并归。
直到自己可以进行排序的数据的大小（这里可以使用自己想用的排序方法！）。

时间复杂度：O（NlgN），基本算法与快速排序最好情况（二分法，这个是完全二分方法）。时间复杂度：O（N + lgN）。

非比较排序

通过计算不同的数字，出现的次数，然后进行书写出现的数字的样子。优化可以选取最小的，和最大的作为计算的开始与结束位置信息！

限制数据集中，在某一个区间内部，时间复杂度为O（n）。

稳定性

定义数据的相对位置不变，在数据相同情况下，保证数据更加公平，例如：考试试卷的问题。