智能优化算法：白鲸优化算法
摘要：白鲸优化算法([Beluga whale optimization，BWO)是由是由 Changting Zhong 等于2022 年提出的一种群体智能优化算法。其灵感来源于白鲸的群体觅食行为。
1.白鲸优化算法
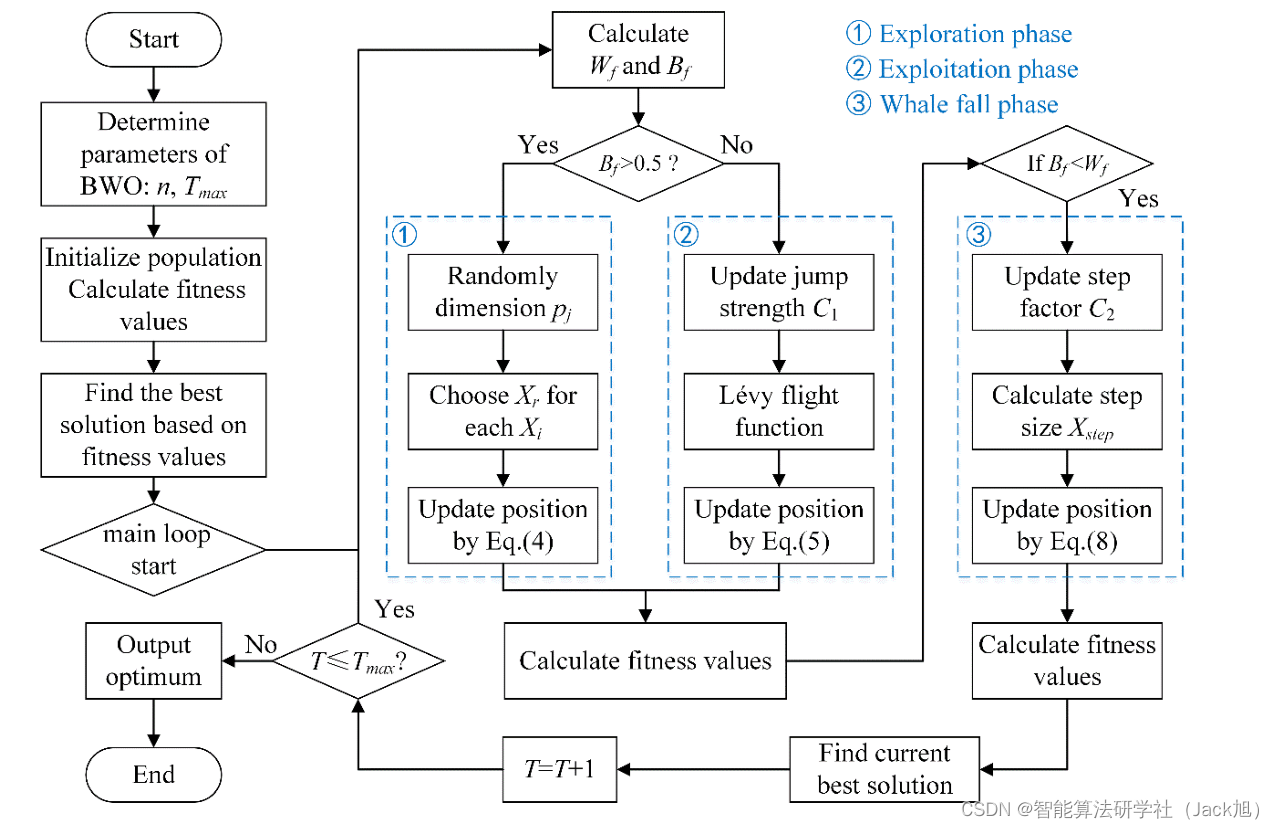
BWO建立了探索、开发和鲸鱼坠落的三个阶段，分别对应于成对游泳、捕食和鲸落的行为。BWO中的平衡因子和鲸落概率是自适应的，对控制探索和开发能力起着重要作用。此外，还引入了莱维飞行来增强开发阶段的全局收敛性。
BWO算法可以从探索逐渐转换到开发，这取决于平衡因子
B
f
\mathrm{~B}_{\mathrm{f}}
Bf ，其定义为:
B
f
=
B
0
(
1
−
T
/
(
2
T
max
)
)
\mathrm{B}_{\mathrm{f}}=\mathrm{B}_0\left(1-\mathrm{T} /\left(2 \mathrm{~T}_{\max }\right)\right)
Bf=B0(1−T/(2 Tmax))
其中，
T
\mathrm{T}
T 是当前迭代次，
T
max
\mathrm{T}_{\max }
Tmax 是最大迭代次数，
B
0
\mathrm{B}_0
B0 在每次迭代中在
(
0
,
1
)
(0,1)
(0,1) 之间随机变化。探索阶段发生在平衡因子
B
f
>
0.5
\mathrm{B}_{\mathrm{f}}>0.5
Bf>0.5 时，而开发 阶段发生在
B
f
≤
0.5
\mathrm{B}_{\mathrm{f}} \leq 0.5
Bf≤0.5 。随着迭代次数
T
\mathrm{T}
T 的增加，
B
f
\mathrm{B}_{\mathrm{f}}
Bf 的波动范围从
(
0
,
1
)
(0,1)
(0,1) 减小到
(
0
,
0.5
)
(0,0.5)
(0,0.5) ，说明开发和探索阶段的概率发生了显著变化，而 开发阶段的概率随着迭代次数
T
\mathrm{T}
T 的不断增加而增加。
1.1 探索阶段
BWO的探索阶段是白鲸的游泳行为建立的。搜索代理的位置由白鲸的配对游泳决定，白鲸的位置更新如下:
{
X
i
,
j
T
+
1
=
X
i
,
p
j
T
+
(
X
r
,
p
1
T
−
X
i
,
p
j
T
)
(
1
+
r
1
)
sin
(
2
π
r
2
)
,
j
=
even
X
i
,
j
T
+
1
=
X
i
,
p
j
T
+
(
X
r
,
p
1
T
−
X
i
,
p
j
T
)
(
1
+
r
1
)
cos
(
2
π
r
2
)
,
j
=
o
d
d
\begin{cases}\mathrm{X}_{\mathrm{i}, \mathrm{j}}^{\mathrm{T+1}}=\mathrm{X}_{\mathrm{i}, \mathrm{p}_{\mathrm{j}}}^{\mathrm{T}}+\left(\mathrm{X}_{\mathrm{r}, \mathrm{p}_1}^{\mathrm{T}}-\mathrm{X}_{\mathrm{i}, \mathrm{p}_{\mathrm{j}}}^{\mathrm{T}}\right)\left(1+\mathrm{r}_1\right) \sin \left(2 \pi \mathrm{r}_2\right), \mathrm{j}=\text { even } \\ \mathrm{X}_{\mathrm{i}, \mathrm{j}}^{\mathrm{T}+1}=\mathrm{X}_{\mathrm{i}, \mathrm{p}_{\mathrm{j}}}^{\mathrm{T}}+\left(\mathrm{X}_{\mathrm{r}, \mathrm{p}_1}^{\mathrm{T}}-\mathrm{X}_{\mathrm{i}, \mathrm{p}_{\mathrm{j}}}^{\mathrm{T}}\right)\left(1+\mathrm{r}_1\right) \cos \left(2 \pi \mathrm{r}_2\right), \quad \mathrm{j}=\mathrm{odd}\end{cases}
⎩⎨⎧Xi,jT+1=Xi,pjT+(Xr,p1T−Xi,pjT)(1+r1)sin(2πr2),j= even Xi,jT+1=Xi,pjT+(Xr,p1T−Xi,pjT)(1+r1)cos(2πr2),j=odd
其中，
T
\mathrm{T}
T 是当前迭代次数，
X
i
,
j
T
+
1
\mathrm{X}_{\mathrm{i}, \mathrm{j}}^{\mathrm{T+1}}
Xi,jT+1 是第i只白鲸在第
j
j
j维上的新位置，
p
j
(
j
=
1
,
2
,
⋯
,
d
)
\mathrm{p}_{\mathrm{j}}(\mathrm{j}=1,2, \cdots, \mathrm{d})
pj(j=1,2,⋯,d) 是从
d
\mathrm{d}
d 维中选择的随机整数，
X
i
,
p
j
T
\mathrm{X}_{\mathrm{i}, \mathrm{p} \mathrm{j}}^{\mathrm{T}}
Xi,pjT 是第i条白鲸 在
p
j
\mathrm{p}_{\mathrm{j}}
pj 维度上的位置，
X
i
,
p
j
T
\mathrm{X}_{\mathrm{i}, \mathrm{p}_{\mathrm{j}}}^{\mathrm{T}}
Xi,pjT 和
X
r
,
p
1
T
\mathrm{X}_{\mathrm{r}, \mathrm{p} 1}^{\mathrm{T}}
Xr,p1T 分别是第1条和第
r
\mathrm{r}
r 条白鲸的当前位置
(
r
\left(\mathrm{r}\right.
(r 是随机选择的白鲸)，随机数
r
1
r_1
r1 和
r
2
r_2
r2 用于增强探索阶段的随机算子 ，
r
1
\mathrm{r}_1
r1 和
r
2
\mathrm{r}_2
r2 是
(
0
,
1
)
(0,1)
(0,1) 的随机数，
sin
(
2
π
r
2
)
\sin \left(2 \pi \mathrm{r}_2\right)
sin(2πr2) 和
sin
(
2
π
r
2
)
\sin \left(2 \pi \mathrm{r}_2\right)
sin(2πr2) 表示镜像白鲸的鲌朝向水面。根据奇偶数选择的维数，更新后的位置反映了白鲸在游泳或跳水时的同步或镜像行为。
1.2 开发阶段
BWO的开发阶段受到白鲸捕食行为的启发。白鲸可以根据附近白鲸的位置合作觅食和移动。因此，白鲸通过共享彼此的位置信息来捕 食，同时考虑最佳候选者和其他候选者。在BWO的开发阶段引入了莱维飞行策略，以增强收敛性。假设它们可以使用莱维飞行策略捕捉 猎物，数学模型表示为：
X
i
T
+
1
=
r
3
X
best
T
−
r
4
X
i
T
+
C
1
⋅
L
F
⋅
(
X
r
T
−
X
i
T
)
\mathrm{X}_{\mathrm{i}}^{\mathrm{T}+1}=\mathrm{r}_3 \mathrm{X}_{\text {best }}^{\mathrm{T}}-\mathrm{r}_4 \mathrm{X}_{\mathrm{i}}^{\mathrm{T}}+\mathrm{C}_1 \cdot \mathrm{L}_{\mathrm{F}} \cdot\left(\mathrm{X}_{\mathrm{r}}^{\mathrm{T}}-\mathrm{X}_{\mathrm{i}}^{\mathrm{T}}\right)
XiT+1=r3Xbest T−r4XiT+C1⋅LF⋅(XrT−XiT)
其中，
T
\mathrm{T}
T 是当前迭代次数，
X
i
T
\mathrm{X}_{\mathrm{i}}^{\mathrm{T}}
XiT 和
X
r
T
\mathrm{X}_{\mathrm{r}}^{\mathrm{T}}
XrT 分别是第
i
\mathrm{i}
i 条白鲸和随机白鲸的当前位置，
X
i
T
+
1
\mathrm{X}_{\mathrm{i}}^{\mathrm{T}+1}
XiT+1 是第
i
\mathrm{i}
i 条白鲸的新位置，
X
b
e
s
t
T
\mathrm{X}_{\mathrm{best}}^{\mathrm{T}}
XbestT 是白鲸种群中的最佳位置，
r
3
\mathrm{r}_3
r3 和
r
4
\mathrm{r}_4
r4 是
(
0
,
1
)
(0,1)
(0,1) 之间的随机数，
C
1
=
2
r
4
(
1
−
T
/
T
max
)
\mathrm{C}_1=2 \mathrm{r}_4\left(1-\mathrm{T} / \mathrm{T}_{\max }\right)
C1=2r4(1−T/Tmax) 是衡量莱维飞行强度的随机跳跃强度。
L
F
\mathrm{L}_{\mathrm{F}}
LF 是莱维飞行函数，计算如下:
L
F
=
0.05
×
u
×
σ
∣
v
∣
1
/
β
σ
=
(
Γ
(
1
+
β
)
×
sin
(
π
β
/
2
)
Γ
(
(
1
+
β
)
/
2
)
×
β
×
2
(
β
−
1
)
/
2
)
1
/
β
\begin{gathered} \mathrm{L}_{\mathrm{F}}=0.05 \times \frac{\mathrm{u} \times \sigma}{|\mathrm{v}|^{1 / \beta}} \\ \sigma=\left(\frac{\Gamma(1+\beta) \times \sin (\pi \beta / 2)}{\Gamma((1+\beta) / 2) \times \beta \times 2^{(\beta-1) / 2}}\right)^{1 / \beta} \end{gathered}
LF=0.05×∣v∣1/βu×σσ=(Γ((1+β)/2)×β×2(β−1)/2Γ(1+β)×sin(πβ/2))1/β
其中，
u
u
u 和
v
v
v 为正态分布随机数，
β
\beta
β 为默认常数，等于1.5。
1.3 鲸鱼坠落
为了在每次迭代中模拟鲸鱼坠落的行为，从种群中的个体中选择鲸鱼坠落概率作为主观假设，以模拟群体中的小变化。假设这些白鲸要 么移到别处，要么被击落并坠入深海。为了确保种群大小的数量恒定，使用白鲸的位置和鲸鱼落体的步长来建立更新的位置。数学模型表 示为：
X
i
T
+
1
=
r
5
X
i
T
−
r
6
X
r
T
+
r
7
X
step
\mathrm{X}_{\mathrm{i}}^{\mathrm{T}+1}=\mathrm{r}_5 \mathrm{X}_{\mathrm{i}}^{\mathrm{T}}-\mathrm{r}_6 \mathrm{X}_{\mathrm{r}}^{\mathrm{T}}+\mathrm{r}_7 \mathrm{X}_{\text {step }}
XiT+1=r5XiT−r6XrT+r7Xstep
其中，
r
5
、
r
6
\mathrm{r}_5 、 \mathrm{r}_6
r5、r6 和
r
7
\mathrm{r}_7
r7 是
(
0
,
1
)
(0,1)
(0,1) 之间的随机数，
X
s
t
e
p
\mathrm{X}_{\mathrm{step}}
Xstep 是鲸鱼坠落的步长，定义为:
X
step
=
(
u
b
−
l
b
)
exp
(
−
C
2
T
/
T
max
)
\mathrm{X}_{\text {step }}=\left(\mathrm{u}_{\mathrm{b}}-\mathrm{l}_{\mathrm{b}}\right) \exp \left(-\mathrm{C}_2 \mathrm{~T} / \mathrm{T}_{\max }\right)
Xstep =(ub−lb)exp(−C2 T/Tmax)
其中，
C
2
\mathrm{C}_2
C2 是与鲸鱼下降概率和种群规模相关的阶跃因子
(
C
2
=
2
W
f
×
n
)
\left(\mathrm{C}_2=2 \mathrm{~W}_{\mathrm{f}} \times \mathrm{n}\right)
(C2=2 Wf×n) ，
u
b
\mathrm{u}_{\mathrm{b}}
ub 和
l
b
\mathrm{l}_{\mathrm{b}}
lb 分别是变量的上下限。可以看出，步长受问题变量边 界、当前迭代次数和最大迭代次数的影响。
在该模型中，鲸鱼坠落概率
(
W
f
)
\left(\mathrm{W}_{\mathrm{f}}\right)
(Wf) 作为线性函数计算:
W
f
=
0.1
−
0.05
T
/
T
max
\mathrm{W}_{\mathrm{f}}=0.1-0.05 \mathrm{~T} / \mathrm{T}_{\max }
Wf=0.1−0.05 T/Tmax
鲸鱼队落的概率从初始迭代的0.1降低到最后一次迭代的
0.05
0.05
0.05 ，表明在优化过程中，当白鲸更接近食物源时，白鲸的危险性降低。
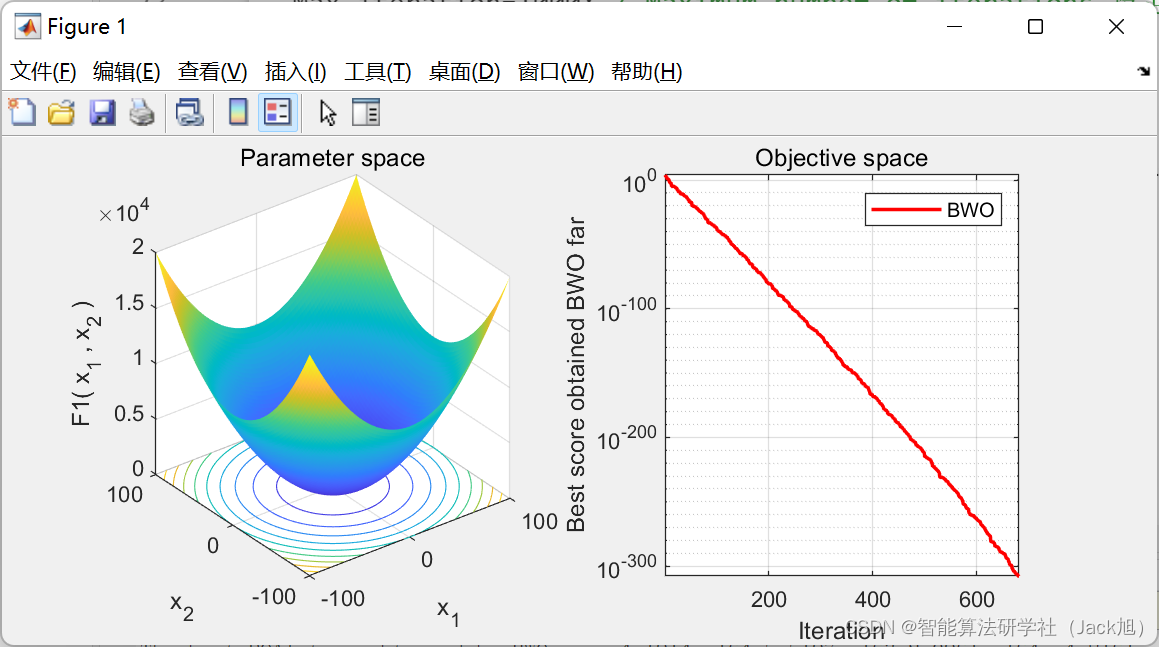
3.实验结果
4.参考文献
[1] Changting Zhong, Gang Li, Zeng Meng. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm[J]. Knowledge-Based Systems, 2022, 251: 109215.
5.Matlab代码
6.python代码
本文转载自: https://blog.csdn.net/u011835903/article/details/127642354
版权归原作者 智能算法研学社（Jack旭） 所有， 如有侵权，请联系我们删除。
版权归原作者 智能算法研学社（Jack旭） 所有， 如有侵权，请联系我们删除。