机器学习笔记之深度玻尔兹曼机——玻尔兹曼机系列整体介绍
引言
从本节开始,将介绍玻尔兹曼机系列的最后一个模型——深度玻尔兹曼机(Deep Boltzmann Machine,DBM)
关于含隐变量模型的对数似然梯度
在之前介绍的包含隐变量的能量模型如波尔兹曼机、受限波尔兹曼机,其能量模型的结构均可表示为如下形式:
本质上就是包含隐变量的马尔可夫随机场~
P
(
X
)
=
1
Z
∑
i
=
1
K
ψ
i
(
x
C
i
)
\begin{aligned} \mathcal P(\mathcal X) = \frac{1}{\mathcal Z} \sum_{i=1}^{\mathcal K} \psi_{i}(x_{\mathcal C_i}) \end{aligned}
P(X)=Z1i=1∑Kψi(xCi)
其中
X
\mathcal X
X
表示随机变量集合(包含隐变量、观测变量);
x
C
i
(
i
=
1
,
2
,
⋯
,
K
)
x_{\mathcal C_i}(i=1,2,\cdots,\mathcal K)
xCi(i=1,2,⋯,K)
表示极大团;对应的
ψ
i
(
x
C
i
)
\psi_i(x_{\mathcal C_i})
ψi(xCi)
表示该极大团对应的势函数。由于势函数的非负性质,因此如果从能量模型的角度观察势函数,可将
P
(
X
)
\mathcal P(\mathcal X)
P(X)
表示为如下形式:
P
(
X
)
=
P
(
h
,
v
)
=
1
Z
exp
{
−
E
[
h
,
v
]
}
\begin{aligned} \mathcal P(\mathcal X) & = \mathcal P(h,v) \\ & = \frac{1}{\mathcal Z} \exp \left\{-\mathbb E[h,v]\right\} \end{aligned}
P(X)=P(h,v)=Z1exp{−E[h,v]}
其中
Z
\mathcal Z
Z
表示‘配分函数’,具体可表示为
Z
=
∑
h
,
v
exp
{
−
E
[
h
,
v
]
}
\mathcal Z = \sum_{h,v} \exp \left\{-\mathbb E[h,v]\right\}
Z=∑h,vexp{−E[h,v]}.
关于该模型的对数似然函数可表示为:
系数1 N \frac{1}{N} N1为后续计算方便所添加的结果,在‘极大似然估计’中,该系数并不影响‘最优模型参数’θ \theta θ的结果。其中V \mathcal V V表示观测变量产生的实际样本集合:V = { v ( i ) } i = 1 N \mathcal V = {v^{(i)}}_{i=1}^N V={v(i)}i=1N,N N N表示样本数量。对应地,h ( i ) h^{(i)} h(i)表示某样本v ( i ) v^{(i)} v(i)在模型中对应的隐变量集合。L ( θ ) = log P ( V ; θ ) = log ∏ i = 1 N P ( v ( i ) ; θ ) ∝ 1 N ∑ i = 1 N log P ( v ( i ) ; θ ) = 1 N ∑ i = 1 N log [ ∑ h ( i ) P ( h ( i ) , v ( i ) ; θ ) ] \begin{aligned} \mathcal L(\theta) & = \log \mathcal P(\mathcal V;\theta) \ & = \log \prod_{i=1}^N \mathcal P(v^{(i)};\theta) \ & \propto \frac{1}{N} \sum_{i=1}^N \mathcal \log P(v^{(i)};\theta) \ & = \frac{1}{N} \sum_{i=1}^N \log \left[\sum_{h^{(i)}} \mathcal P(h^{(i)},v^{(i)};\theta)\right] \end{aligned} L(θ)=logP(V;θ)=logi=1∏NP(v(i);θ)∝N1i=1∑NlogP(v(i);θ)=N1i=1∑Nlog[h(i)∑P(h(i),v(i);θ)]
将能量函数代入,对应的对数似然梯度
∇
θ
L
(
θ
)
\nabla_{\theta} \mathcal L(\theta)
∇θL(θ)可表示为:
求解过程详见
受限玻尔兹曼机——基于含隐变量能量模型的对数似然梯度
∇
θ
L
(
θ
)
=
1
N
∑
i
=
1
N
∇
θ
[
log
P
(
v
(
i
)
;
θ
)
]
=
1
N
∑
i
=
1
N
{
∑
h
(
i
)
,
v
(
i
)
[
P
(
h
(
i
)
,
v
(
i
)
)
⋅
∇
θ
E
(
h
(
i
)
,
v
(
i
)
)
]
−
∑
h
(
i
)
[
P
(
h
(
i
)
∣
v
(
i
)
)
⋅
∇
θ
E
(
h
(
i
)
,
v
(
i
)
)
]
}
\begin{aligned} \nabla_{\theta}\mathcal L(\theta) & = \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right] \\ & = \frac{1}{N} \sum_{i=1}^N \left\{ \sum_{h^{(i)},v^{(i)}} \left[\mathcal P(h^{(i)},v^{(i)}) \cdot \nabla_{\theta} \mathbb E(h^{(i)},v^{(i)})\right] - \sum_{h^{(i)}} \left[\mathcal P(h^{(i)} \mid v^{(i)}) \cdot \nabla_{\theta} \mathbb E(h^{(i)},v^{(i)})\right]\right\} \end{aligned}
∇θL(θ)=N1i=1∑N∇θ[logP(v(i);θ)]=N1i=1∑N⎩⎨⎧h(i),v(i)∑[P(h(i),v(i))⋅∇θE(h(i),v(i))]−h(i)∑[P(h(i)∣v(i))⋅∇θE(h(i),v(i))]⎭⎬⎫
玻尔兹曼机
玻尔兹曼机本质上是一个马尔可夫随机场(无向图模型),概率图中的随机变量结点均是服从伯努利分布的离散型随机变量。
从随机变量的性质角度,可将随机变量划分成两个部分:**观测变量
v
v
v、隐变量
h
h
h**:
这里的
v
,
h
v,h
v,h
表示随机变量集合,并定义
v
v
v
中包含
D
\mathcal D
D
个随机变量,
h
h
h
中包含
P
\mathcal P
P
个随机变量。
{
v
=
(
v
1
,
v
2
,
⋯
,
v
D
)
T
;
v
∈
{
0
,
1
}
D
h
=
(
h
1
,
h
2
,
⋯
,
h
P
)
T
;
h
∈
{
0
,
1
}
P
\begin{cases} v = \left(v_1,v_2,\cdots,v_{\mathcal D}\right)^T;v \in \{0,1\}^{\mathcal D} \\ h = \left(h_1,h_2,\cdots,h_{\mathcal P}\right)^T; h \in \{0,1\}^{\mathcal P} \end{cases}
{v=(v1,v2,⋯,vD)T;v∈{0,1}Dh=(h1,h2,⋯,hP)T;h∈{0,1}P
对应的概率图结构可表示如下:
下图是一个全连接的特殊情况,即无论是观测变量还是隐变量,两两之间均存在关联关系。而实际上可能仅是观测变量、隐变量的无向图结构而已。
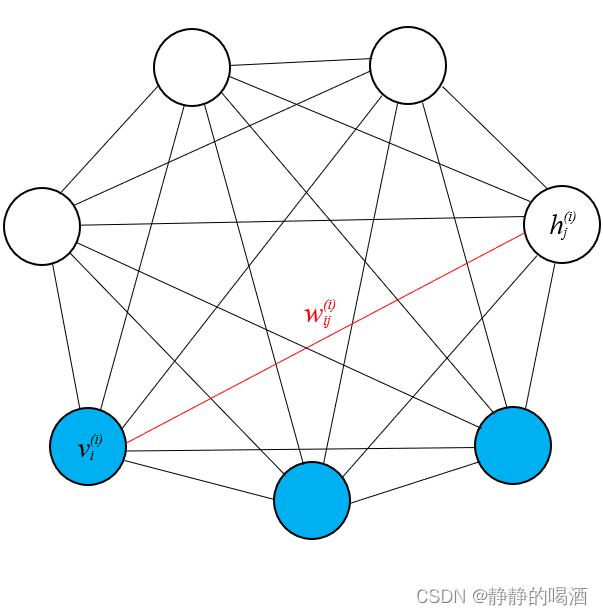
关于波尔兹曼机的能量函数可表示为:
E
(
v
,
h
)
=
−
[
v
T
W
⋅
h
+
1
2
v
T
L
⋅
v
+
1
2
h
T
J
⋅
h
]
\mathbb E(v,h) = - \left[v^T\mathcal W \cdot h + \frac{1}{2}v^T \mathcal L \cdot v + \frac{1}{2}h^T \mathcal J \cdot h\right]
E(v,h)=−[vTW⋅h+21vTL⋅v+21hTJ⋅h]
将能量函数
E
(
v
,
h
)
\mathbb E(v,h)
E(v,h)代入到**对数似然函数**中,可得到关于**波尔兹曼机**的对数似然梯度:
根据能量函数的表示,发现明显存在三个参数:
W
,
L
,
J
\mathcal W,\mathcal L,\mathcal J
W,L,J
,因此需要对三个参数分别求解梯度。以模型参数
W
\mathcal W
W
(麻烦)为例,其推导过程详见
玻尔兹曼机——基本介绍
∇
W
L
(
θ
)
=
1
N
∑
i
=
1
N
∇
W
[
log
P
(
v
(
i
)
;
θ
)
]
≈
E
P
d
a
t
a
[
v
(
i
)
(
h
(
i
)
)
T
]
−
E
P
m
o
d
e
l
[
v
(
i
)
(
h
(
i
)
)
T
]
{
P
d
a
t
a
=
P
d
a
t
a
(
v
(
i
)
,
h
(
i
)
)
=
P
d
a
t
a
(
v
(
i
)
∈
V
)
⋅
P
m
o
d
e
l
(
h
(
i
)
∣
v
(
i
)
)
P
m
o
d
e
l
=
P
m
o
d
e
l
(
v
(
i
)
,
h
(
i
)
)
\begin{aligned} \nabla_{\mathcal W}\mathcal L(\theta) & = \frac{1}{N} \sum_{i=1}^N \nabla_{\mathcal W} \left[\log \mathcal P(v^{(i)};\theta)\right] \\ & \approx \mathbb E_{\mathcal P_{data}} \left[v^{(i)}(h^{(i)})^T\right] - \mathbb E_{\mathcal P_{model}} \left[v^{(i)}(h^{(i)})^T\right] \end{aligned} \\ \begin{cases} \mathcal P_{data} = \mathcal P_{data}(v^{(i)},h^{(i)}) = \mathcal P_{data}(v^{(i)} \in \mathcal V) \cdot \mathcal P_{model}(h^{(i)} \mid v^{(i)}) \\ \mathcal P_{model} = \mathcal P_{model}(v^{(i)},h^{(i)}) \end{cases}
∇WL(θ)=N1i=1∑N∇W[logP(v(i);θ)]≈EPdata[v(i)(h(i))T]−EPmodel[v(i)(h(i))T]{Pdata=Pdata(v(i),h(i))=Pdata(v(i)∈V)⋅Pmodel(h(i)∣v(i))Pmodel=Pmodel(v(i),h(i))
可以同过上式发现,梯度上升迭代过程中,模型参数
W
\mathcal W
W梯度的计算主要分为两个部分:**正相(
Positive Phase
\text{Positive Phase}
Positive Phase)与负相(
Negative Phase
\text{Negative Phase}
Negative Phase)**:
E
P
d
a
t
a
[
v
(
i
)
(
h
(
i
)
)
T
]
⏟
Positive Phase
−
E
P
m
o
d
e
l
[
v
(
i
)
(
h
(
i
)
)
T
]
⏟
Negative Phase
\underbrace{\mathbb E_{\mathcal P_{data}} \left[v^{(i)}(h^{(i)})^T\right]}_{\text{Positive Phase}}- \underbrace{\mathbb E_{\mathcal P_{model}} \left[v^{(i)}(h^{(i)})^T\right]}_{\text{Negative Phase}}
Positive PhaseEPdata[v(i)(h(i))T]−Negative PhaseEPmodel[v(i)(h(i))T]
从关于
P
d
a
t
a
\mathcal P_{data}
Pdata的描述也可以看出来,**依赖数据**(
Data Dependent
\text{Data Dependent}
Data Dependent) 所产生的**联合概率分布**
P
d
a
t
a
(
v
(
i
)
,
h
(
i
)
)
\mathcal P_{data}(v^{(i)},h^{(i)})
Pdata(v(i),h(i))由两部分构成:
- 基于真实样本 v ( i ) ∈ V v^{(i)} \in \mathcal V v(i)∈V的关于观测变量的边缘概率分布 P d a t a ( v ( i ) ) \mathcal P_{data}(v^{(i)}) Pdata(v(i));
- 在真实样本给定的条件下,模型内部隐变量的后验概率分布 P m o d e l ( h ( i ) ∣ v ( i ) ) \mathcal P_{model}(h^{(i)} \mid v^{(i)}) Pmodel(h(i)∣v(i));
隐变量h ( i ) h^{(i)} h(i)从始至终都是依赖于模型存在的,因此写作P m o d e l ( h ( i ) ∣ v ( i ) ) \mathcal P_{model}(h^{(i)} \mid v^{(i)}) Pmodel(h(i)∣v(i)).
而 不依赖数据(
Data Independent
\text{Data Independent}
Data Independent),仅通过模型产生的**联合概率分布**
P
m
o
d
e
l
(
v
(
i
)
,
h
(
i
)
)
\mathcal P_{model}(v^{(i)},h^{(i)})
Pmodel(v(i),h(i))不包含任何真实样本的参与,甚至生成的样本也被称为**幻想粒子**(
Fantasy Particle
\text{Fantasy Particle}
Fantasy Particle)。
而正相、负相均采用MCMC进行求解。其思想是:**由于观测变量、隐变量内部也存在关联关系,因而无法求解后验概率
P
(
h
∣
v
)
\mathcal P(h \mid v)
P(h∣v)。因此它针对当个变量的后验概率进行表示**:
其中
v
−
i
v_{-i}
v−i
表示除去观测变量
v
i
v_i
vi
之外的其他观测变量。
详细推导过程详见
玻尔兹曼机——梯度求解
P
(
v
i
(
i
)
∣
h
(
i
)
,
v
−
i
(
i
)
)
v
(
i
)
∈
{
0
,
1
}
∣
D
∣
;
h
(
i
)
∈
{
0
,
1
}
∣
P
∣
\mathcal P(v_i^{(i)} \mid h^{(i)},v_{-i}^{(i)}) \quad v^{(i)} \in \{0,1\}^{|\mathcal D|};h^{(i)} \in \{0,1\}^{|\mathcal P|}
P(vi(i)∣h(i),v−i(i))v(i)∈{0,1}∣D∣;h(i)∈{0,1}∣P∣
玻尔兹曼机的缺陷是明显的——随机变量结点数过多,算力跟不上。由于任意随机变量之间都有可能存在关联关系,这样模型的计算是复杂的,在MCMC采样过程中,随机变量结点过多导致极难达到平稳分布。
这种模型可能仅在理论中实现,实用性基本是没有的。
受限玻尔兹曼机
相比于玻尔兹曼机,受限玻尔兹曼机对于随机变量的约束进行了提升。主要表现在:隐变量、观测变量 之间存在关联关系,其内部随机变量之间相互独立: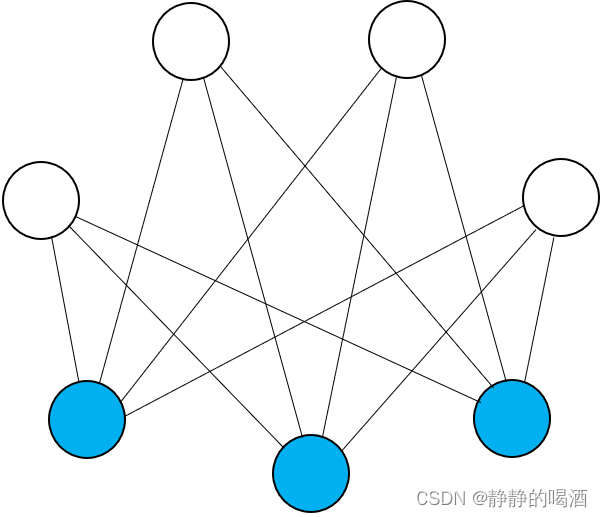
不同于玻尔兹曼机的混乱结构,经过约束后的受限玻尔兹曼机存在明显的层级结构——观测变量层、隐变量层。
关于受限玻尔兹曼机的能量函数可表示为:
E
(
v
,
h
)
=
−
(
v
T
W
⋅
h
+
b
T
v
+
c
T
h
)
\mathbb E(v,h) = - \left(v^T \mathcal W \cdot h + b^T v + c^T h\right)
E(v,h)=−(vTW⋅h+bTv+cTh)
对应的模型参数为:
W
,
b
,
c
\mathcal W,b,c
W,b,c。其中
b
,
c
b,c
b,c分别表示一个**列向量**,并且其向量中的每一个元素均表示**某结点与自身的关联关系信息**。
由于结点与同层中的其他结点之间均不存在关联关系,因此这里的
b
,
c
b,c
b,c
视作‘偏置项’信息即可。
关于受限玻尔兹曼机关于模型参数的学习任务表示如下。将受限玻尔兹曼机的能量函数带入到对数似然梯度中:
这里的
θ
\theta
θ
是指某样本
v
(
i
)
v^{(i)}
v(i)
对应的某一观测变量
v
j
(
i
)
v_j^{(i)}
vj(i)
与该样本对应模型中的某一隐变量
h
k
(
i
)
h_k^{(i)}
hk(i)
之间关联关系的参数信息
W
k
j
(
i
)
\mathcal W_{kj}^{(i)}
Wkj(i).
详细推导过程见
受限玻尔兹曼机——对数似然梯度求解
需要再次强调一下,关于大括号内的项对于
∇
θ
[
log
P
(
v
(
i
)
;
θ
)
]
\nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right]
∇θ[logP(v(i);θ)]
的表示并不完整,其内部只是关于模型参数
W
k
j
(
i
)
\mathcal W_{kj}^{(i)}
Wkj(i)
的梯度信息
.
∇
θ
L
(
θ
)
=
1
N
∑
i
=
1
N
∇
θ
[
log
P
(
v
(
i
)
;
θ
)
]
θ
=
W
k
j
(
i
)
=
1
N
∑
i
=
1
N
{
∑
h
(
i
)
[
P
(
h
(
i
)
∣
v
(
i
)
)
⋅
(
−
h
k
(
i
)
v
j
(
i
)
)
]
+
∑
h
(
i
)
,
v
(
i
)
[
P
(
h
(
i
)
,
v
(
i
)
)
⋅
(
−
h
k
(
i
)
v
j
(
i
)
)
]
}
=
1
N
∑
i
=
1
N
{
P
(
h
k
(
i
)
=
1
∣
v
(
i
)
)
⋅
v
j
(
i
)
−
∑
v
(
i
)
P
(
v
(
i
)
)
⋅
P
(
h
k
(
i
)
=
1
∣
v
(
i
)
)
⋅
v
j
(
i
)
}
\begin{aligned} \nabla_{\theta}\mathcal L(\theta) & = \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right] \quad \theta = \mathcal W_{kj}^{(i)}\\ & = \frac{1}{N} \sum_{i=1}^N \left\{ \sum_{h^{(i)}} \left[\mathcal P(h^{(i)} \mid v^{(i)}) \cdot (- h_k^{(i)}v_j^{(i)})\right] + \sum_{h^{(i)},v^{(i)}} \left[\mathcal P(h^{(i)},v^{(i)}) \cdot (-h_k^{(i)}v_j^{(i)})\right]\right\} \\ & = \frac{1}{N} \sum_{i=1}^N \left\{\mathcal P(h_k^{(i)}=1 \mid v^{(i)}) \cdot v_j^{(i)} - \sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}\right\} \end{aligned}
∇θL(θ)=N1i=1∑N∇θ[logP(v(i);θ)]θ=Wkj(i)=N1i=1∑N⎩⎨⎧h(i)∑[P(h(i)∣v(i))⋅(−hk(i)vj(i))]+h(i),v(i)∑[P(h(i),v(i))⋅(−hk(i)vj(i))]⎭⎬⎫=N1i=1∑N{P(hk(i)=1∣v(i))⋅vj(i)−v(i)∑P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)}
其中关于大括号内的积分项
∑
v
(
i
)
P
(
v
(
i
)
)
⋅
P
(
h
k
(
i
)
=
1
∣
v
(
i
)
)
⋅
v
j
(
i
)
\sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}
∑v(i)P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i),它的连加项数量于**样本数量**相关,直接求解的代价是极大的。因此关于该项的求解使用**块吉布斯采样**(Block Gibbs Sampling)进行近似求解:
块吉布斯采样的优势在于,由于隐变量、观测变量内部随机变量之间条件独立,因此关于随机变量的采样均可同步进行,而不需要使用基于‘坐标上升法’的吉布斯采样方式。因此,该方法比真正的吉布斯采样要简化许多。
∑
v
(
i
)
P
(
v
(
i
)
)
⋅
P
(
h
k
(
i
)
=
1
∣
v
(
i
)
)
⋅
v
j
(
i
)
=
E
v
(
k
)
∼
P
d
a
t
a
[
P
(
h
k
(
i
)
=
1
∣
v
(
i
)
)
⋅
v
j
(
i
)
]
\sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)} = \mathbb E_{v^{(k)} \sim \mathcal P_{data}} \left[\mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}\right]
v(i)∑P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)=Ev(k)∼Pdata[P(hk(i)=1∣v(i))⋅vj(i)]
当然,即便块吉布斯采样虽然可以简化过程,但每次迭代需要收敛至平稳分布依然是十分消耗时间的。对此,使用对比散度方法优化吉布斯采样的效率。以精度换效率,加快其迭代速度。
个人理解:这种方式与强化学习中的
广义策略迭代(Generalized Policy Iteration,GPI)
思想非常相似。简单来说,只要更新了,无论更新是否完全,都是向正确方向迭代。而最终都会向最优方向收敛。
对比散度也是这种思想,每次迭代都仅向前执行
k
k
k
步,无论第
k
k
k
步是否是平稳分布,都会停止。它的底层逻辑是“第
k
k
k
步的迭代结果至少比没有迭代的更接近平稳分布。”
相反地,对比散度算法在受限玻尔兹曼机的学习过程被证明成功后,对于玻尔兹曼机的学习过程也被进行改进。
- 关于 P d a t a ( v ( i ) , h ( i ) ) = P d a t a ( v ( i ) ∈ V ) ⋅ P m o d e l ( h ( i ) ∣ v ( i ) ) \mathcal P_{data}(v^{(i)},h^{(i)}) = \mathcal P_{data}(v^{(i)} \in \mathcal V) \cdot \mathcal P_{model}(h^{(i)} \mid v^{(i)}) Pdata(v(i),h(i))=Pdata(v(i)∈V)⋅Pmodel(h(i)∣v(i))中,关于隐变量的后验分布 P m o d e l ( h ( i ) ∣ v ( i ) ) \mathcal P_{model}(h^{(i)} \mid v^{(i)}) Pmodel(h(i)∣v(i))使用基于平均场理论——变分推断进行表达。
- 关于生成过程中的联合概率分布 P m o d e l ( v ( i ) , h ( i ) ) \mathcal P_{model}(v^{(i)},h^{(i)}) Pmodel(v(i),h(i))通过序列化对比散度(Persistent Contrast Divergence)进行求解。
深度信念网络
深度信念网络的底层思想是将**相比于模型参数本身求解隐变量的边缘概率分布
P
(
h
(
i
)
)
\mathcal P(h^{(i)})
P(h(i)),通过对隐变量进行建模,通过极大似然估计求解对数似然函数
log
P
(
h
(
i
)
)
\log \mathcal P(h^{(i)})
logP(h(i))的方式求解
P
(
h
(
i
)
)
\mathcal P(h^{(i)})
P(h(i))的最优解**,最终对**样本**的对数似然梯度
log
P
(
v
(
i
)
)
\log \mathcal P(v^{(i)})
logP(v(i))进行提升。
在深度信念网络——背景介绍与结构表示中关于传统受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)对于隐变量的边缘概率分布
P
(
h
)
\mathcal P(h)
P(h)表示如下:
P
(
v
)
=
∑
h
P
(
h
)
⋅
P
(
v
∣
h
)
{
P
(
v
)
=
∏
v
(
i
)
∈
V
P
(
v
(
i
)
)
P
(
v
∣
h
)
=
∏
j
=
1
∣
D
∣
P
(
v
j
∣
h
)
P
(
v
j
∣
h
)
=
Sigmoid
(
∑
k
=
1
∣
P
∣
w
j
k
⋅
h
k
+
b
j
)
\begin{aligned} & \mathcal P(v) = \sum_{h} \mathcal P(h) \cdot \mathcal P(v \mid h) \\ & \begin{cases} \mathcal P(v) = \prod_{v^{(i)} \in \mathcal V} \mathcal P(v^{(i)}) \\ \mathcal P(v \mid h) = \prod_{j=1}^{|\mathcal D|} \mathcal P(v_j \mid h) \\ \mathcal P(v_j \mid h) = \text{Sigmoid}\left(\sum_{k=1}^{|\mathcal P|} w_{jk} \cdot h_k + b_j\right) \end{cases} \end{aligned}
P(v)=h∑P(h)⋅P(v∣h)⎩⎨⎧P(v)=∏v(i)∈VP(v(i))P(v∣h)=∏j=1∣D∣P(vj∣h)P(vj∣h)=Sigmoid(∑k=1∣P∣wjk⋅hk+bj)
最终可以实现使用模型参数对
P
(
h
)
\mathcal P(h)
P(h)进行表示。但这种表示仅是通过**梯度上升法**对模型参数更新时,
P
(
h
)
\mathcal P(h)
P(h)仅是被**联代**着被更新,可能并没有达到**当前迭代步骤**关于
P
(
h
)
\mathcal P(h)
P(h)的最优解。
因此,**叠加
RBM
\text{RBM}
RBM结构**是基于训练出更优秀的
P
(
h
)
\mathcal P(h)
P(h),从而产生**更优秀的**
P
(
v
)
\mathcal P(v)
P(v)的一种思想。但叠加
RBM
\text{RBM}
RBM结构 **并不是单纯在已知的
RBM
\text{RBM}
RBM结构上堆叠另一个
RBM
\text{RBM}
RBM**,在深度信念网络——模型构建思想(叠加RBM结构)中介绍过,如果将
RBM
\text{RBM}
RBM中的无向边视作**相互关联**的话(即两个结点间存在两个有向边并相互关联):

在**叠加
RBM
\text{RBM}
RBM结构**过程中,会存在
V
\mathcal V
V**型结构**:
为了方便观察,这里仅拆解一个部分。
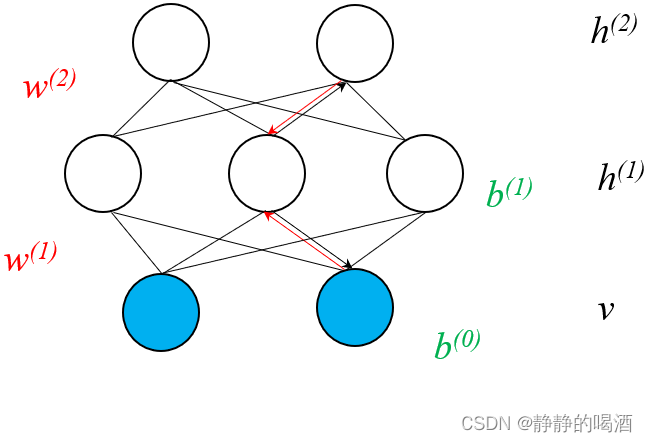
这意味着,单纯地叠加一层
RBM
\text{RBM}
RBM结构,当
h
(
1
)
h^{(1)}
h(1)层**被观测**(通过
P
(
h
(
1
)
∣
v
)
\mathcal P(h^{(1)} \mid v)
P(h(1)∣v)产生样本)时,
h
(
2
)
,
v
h^{(2)},v
h(2),v层结点之间存在**关联关系**,这违背了**受限波尔兹曼机**的模型结构初衷。为了修改这个问题,只能将
h
(
1
)
,
v
h^{(1)},v
h(1),v之间红色有向边去除,最终得到**深度信念网络**的结构表示。
此时,观测变量层
v
v
v
与
h
(
2
)
h^{(2)}
h(2)
层之间必然相互独立。
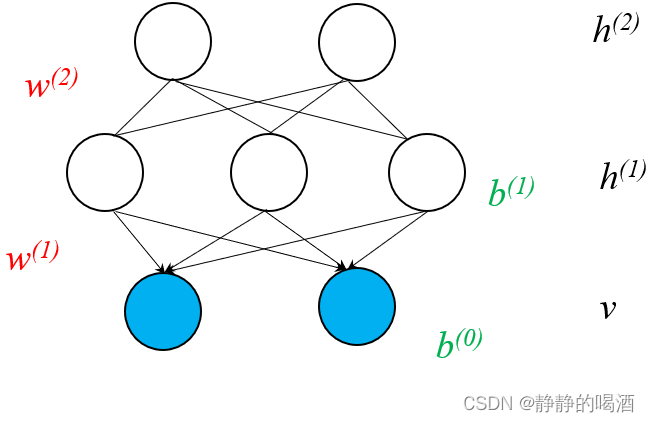
关于该模型参数的学习任务,主要分为如下两个步骤:
- 关于Pre-training的部分:主要是贪心逐层预训练算法。将 Sigmoid \text{Sigmoid} Sigmoid信念网络视作受限玻尔兹曼机来求解后验概率 P ( h ( 1 ) ∣ v ) \mathcal P(h^{(1)} \mid v) P(h(1)∣v),然后逐层向上,忽视其他层对当前遍历层的影响,最终可以得到所有随机变量结点的初始参数信息。
- 关于fine-tuning的部分:在深度信念网络中,介绍它关于模型参数的学习算法——醒眠算法。因此在后续迭代过程中可以尝试使用 Weak Phase \text{Weak Phase} Weak Phase去替代贪心逐层预训练中的算法求解 P ( h ( 1 ) ∣ v ) \mathcal P(h^{(1)} \mid v) P(h(1)∣v)——变种醒眠算法; 如果是有监督学习,可以将深度信念网络当成前馈神经网络进行训练,使用反向传播算法(Back Propagation,BP)对模型参数进行学习。
深度玻尔兹曼机
深度玻尔兹曼机(Deep Boltzmann Machine)它的模型结构表示如下:
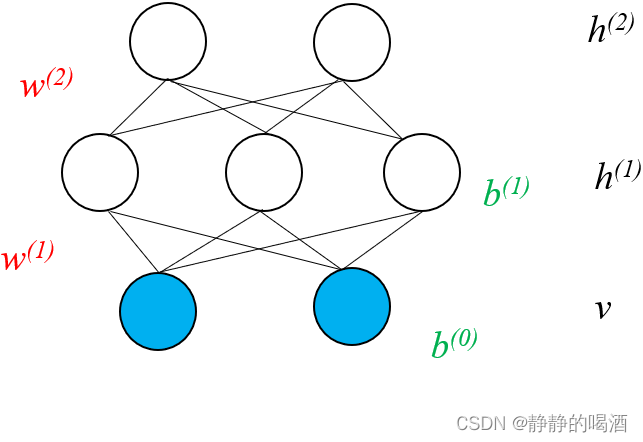
关于它的训练过程与深度信念网络相似,也可以通过预训练(Pre-training)以及后续微调(Fine-tuning)的步骤中进行求解。由于深度玻尔兹曼机也是一种玻尔兹曼机,因此关于模型参数的微调过程同样可以使用玻尔兹曼机中求解对数似然梯度的方式进行近似求解。
后续主要关注深度玻尔兹曼机是如何实现预训练过程的。
相关参考:
深度玻尔兹曼机1-背景介绍
版权归原作者 静静的喝酒 所有, 如有侵权,请联系我们删除。