二叉搜索树

⭐️前言⭐️

本篇文章——二叉搜索树既是对之前的文章【树与二叉树】的一些补充，也是给后续文章TreeMap和TreeSet接口介绍的铺垫。

🍉博客主页：****🍁【如风暖阳】🍁
🍉精品Java专栏【JavaSE】、【备战蓝桥】、【JavaEE初阶】、【MySQL】、【数据结构】
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁

🍉本文由 【如风暖阳】 原创，首发于 CSDN🙉

🍉博主将持续更新学习记录收获，友友们有任何问题可以在评论区留言

🍉博客中涉及源码及博主日常练习代码均已上传码云(gitee)、GitHub

在这里给大家推荐博主常用到的刷题网站【牛客网】,剑指Offer专栏是面试笔试题目高频题单，赶快刷起来吧！

📍内容导读📍

二叉搜索树

🍅1.概念

二叉搜索树又称作二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树：

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树
• 二叉搜索树的中序遍历结果是有序的

如下图所示就是一棵二叉搜索树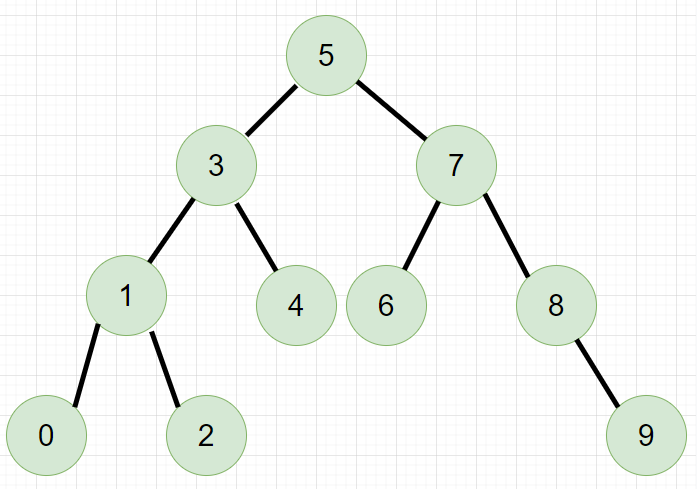

先通过代码完成二叉搜索树的基本构造：

publicclassBinarySearchTree{staticclassTreeNode{publicint val;publicTreeNode left;publicTreeNode right;publicTreeNode(int val){this.val = val;}}publicTreeNode root;}

🍅2.查找操作

在搜索树中查找关键值，因为二叉搜索树的特性，所以可以将关键值与根节点值比较，如果比根节点值小，就去左子树中寻找，反之去右子树中寻找。

publicTreeNodesearch(int key){TreeNode cur=root;while(cur!=null){if(cur.val<key){
                cur=cur.right;}elseif(cur.val>key){
                cur=cur.left;}else{return cur;}}//走到这里说明没有找到关键字returnnull;}

🍅3.插入操作

插入操作依然遵循二叉搜索树的特性，与根节点值进行比较，如果比它小就往左子树中插入，如果比它大就往右子树中插入，可以发现，最后都是插入到了叶子节点上。因为插入操作需要让上一个节点有引用指向插入节点，所以需要使用两个节点。

publicbooleaninsert(int key){TreeNode node=newTreeNode(key);//空树直接插入if(root==null){
            root=node;returntrue;}TreeNode cur=root;TreeNode parent=null;//用于存储上一个节点的引用while(cur!=null){if(cur.val<key){
                parent=cur;
                cur=cur.right;}elseif(cur.val>key){
                parent=cur;
                cur=cur.left;}else{//存在相同的元素 则不能插入成功returnfalse;}}//代码走到这里，cur==null，根据与上一个节点parent的val的比较，确定插入该结点的左还是右if(parent.val<key){
            parent.right=node;}else{
            parent.left=node;}returntrue;}

🍅4.删除操作

二叉搜索树的删除操作十分复杂，首先需要找到要删除的节点，但是该结点可能有左右子树，所以不能直接删除，需要分情况来确定具体的删除方式，如下：

设待删除结点为 cur, 待删除结点的父结点为 parent
1.cur.left == null

• cur 是 root，则 root = cur.right
• cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
• cur 不是 root，cur 是 parent.right，则 parent.right = cur.right

2.cur.right == null

• cur 是 root，则 root = cur.left
• cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
• cur 不是 root，cur 是 parent.right，则 parent.right = cur.left

3.cur.left != null && cur.right != null
需要使用替换法进行删除，即在它的右子树中寻找最小值（它一定没有左树）【或者在它的左子树中寻找最大值，它一定没有右树】，用它的值填补到被删除节点中，再来处理该结点的删除问题（处理该结点就和情况1相同，没有左子树）

代码实现：

/**
     * 删除关键字为key的节点
     * @param key
     */publicvoidremove(int key){//先找到该节点TreeNode cur=root;TreeNode parent=null;while(cur!=null){if(cur.val<key){
                parent=cur;
                cur=cur.right;}elseif(cur.val>key){
                parent=cur;
                cur=cur.left;}else{//代码走到此处说明找到了要删除的节点removeNode(cur,parent);}}}/**
     * 进行删除
     * @param cur 要删除的节点
     * @param parent 删除节点的父结点
     */privatevoidremoveNode(TreeNode cur,TreeNode parent){if(cur.left==null){if(cur==root){
                root=root.right;}elseif(cur==parent.left){
                parent.left=cur.right;}else{
                parent.right=cur.right;}}elseif(cur.right==null){if(cur==root){
                root=root.left;}elseif(cur==parent.left){
                parent.left=cur.left;}else{
                parent.right=cur.left;}}else{TreeNode targetParent=cur;//记录用于替换的节点的上一个节点TreeNode target=cur.right;//记录用于替换的节点//在右子树中寻找最小值，就是一直往左走，走到尽头的节点就是最小值while(target.left!=null){
                targetParent=target;
                target=target.left;}//找到用于替换的节点，完成值的替换，再去处理删除这个替换节点
            cur.val=target.val;//此时该节点一定没有左子树，与之前没有左子树的删除方法相同if(targetParent.left==target){
                targetParent.left=target.right;}else{
                targetParent.right=target.right;}}}

🍅5.性能分析

二叉搜索树的插入和删除操作都需要先进性查找，查找效率代表了二叉搜索树中各个操作的性能，根据不同的插入次序，得到的二叉树结构也可能不同。
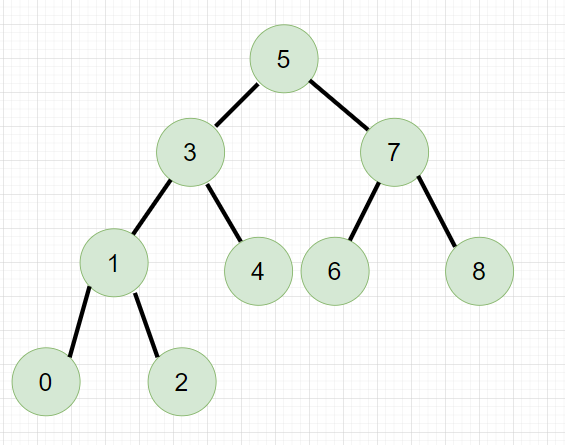
最优情况：
得到一棵完全二叉树
查找的时间复杂度为O（

    l
   
   
    o
   
   
    
     g
    
    
     2
    
   
   
    N
   
  
  
   log_2N
  
 
log2​N）

最差情况：
得到一棵单分支的树
查找的时间复杂度为O(N)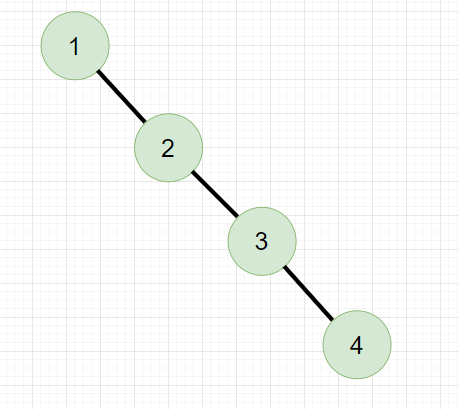

TreeMap 和 TreeSet (这两个接口在后边的文章中介绍)即 java 中利用搜索树实现的 Map 和 Set；实际上用的是红黑树，而红黑树是一棵近似平衡的二叉搜索树，即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证，关于红黑树的内容后序再进行讲解。

⭐️最后的话⭐️
总结不易，希望uu们不要吝啬你们的👍哟(＾Ｕ＾)ノ~ＹＯ！！如有问题，欢迎评论区批评指正😁