LeetCode刷题笔记-数据结构-day16

文章目录

LeetCode刷题笔记-数据结构-day16

199. 二叉树的右视图

1.题目描述

原题链接：199. 二叉树的右视图

2.解题思路

算法：bfs+queue

具体步骤：

1. 用一个队列queue存储每层的节点
2. 每次遍历每层节点，只将队列的第一个加入答案
3. 然后将该层的所有节点的子节点加入队列（先遍历右节点在遍历左节点），每遍历一个节点，该节点就出队
4. 该层节点出队后，进入下一层遍历，最终队列为空就结束了
5. 最终的答案就是二叉树的右视图

3.代码

classSolution{public:
    vector<int>rightSideView(TreeNode* root){
        vector<int> res;if(!root)return res;
        queue<TreeNode*> q;
        q.push(root);while(q.size()){int k=q.size();
            res.push_back(q.front()->val);while(k--){
                auto t=q.front();if(t->right) q.push(t->right);if(t->left) q.push(t->left);
                q.pop();}}return res;}};

113. 路径总和 II

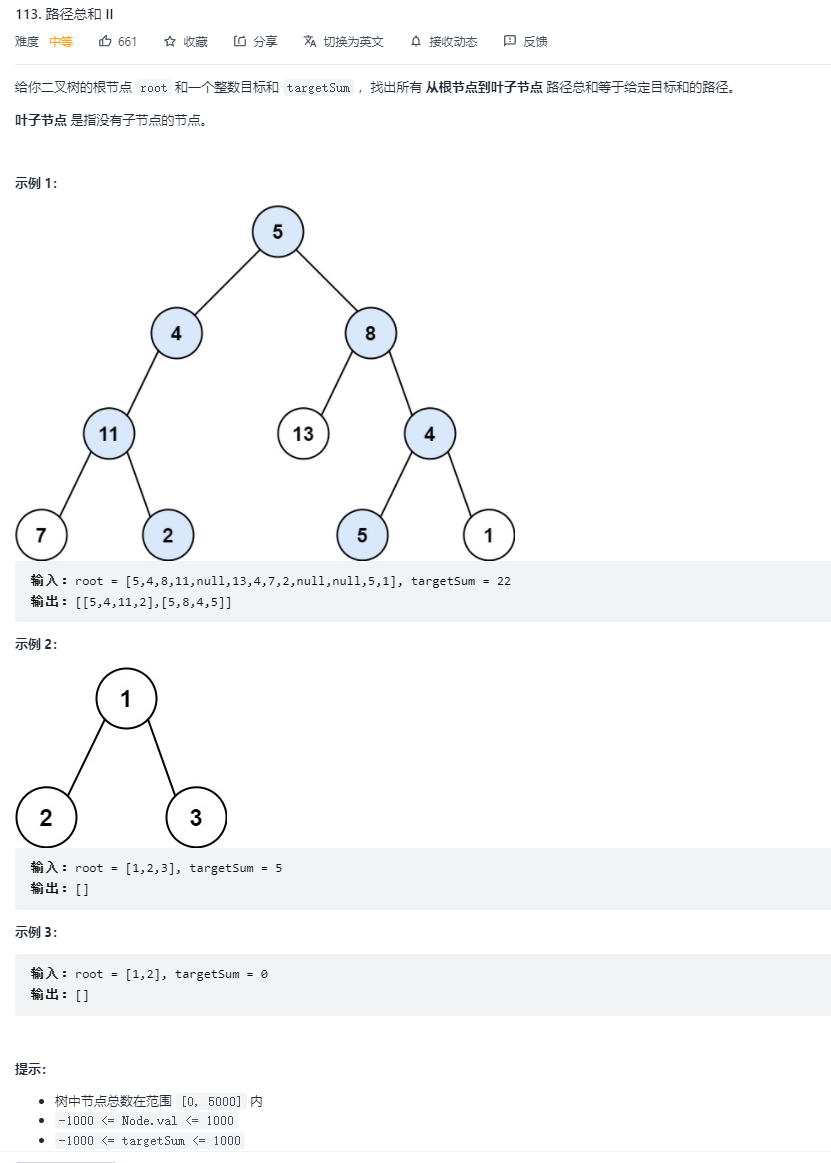
1.题目描述

原题链接：113. 路径总和 II

2.解题思路

算法：递归遍历

具体思路：

1. 用path存放当前路径的所有值，t表示当前路径的和，每次经过减去该节点的值
2. 从根节点开始递归
3. 判断条件：如果该节点是叶子节点并且t为0则表示该条路径符合要求，加入最终答案

3.代码

classSolution{public:
    vector<vector<int>> res;
    vector<vector<int>>pathSum(TreeNode* root,int t){
        vector<int> path;dfs(root,t,path);return res;}voiddfs(TreeNode* root,int t,vector<int> path){if(!root)return;
        t-=root->val;
        path.push_back(root->val);if(!root->left&&!root->right){if(t==0) res.push_back(path);}dfs(root->left,t,path);dfs(root->right,t,path);}};

450. 删除二叉搜索树中的节点

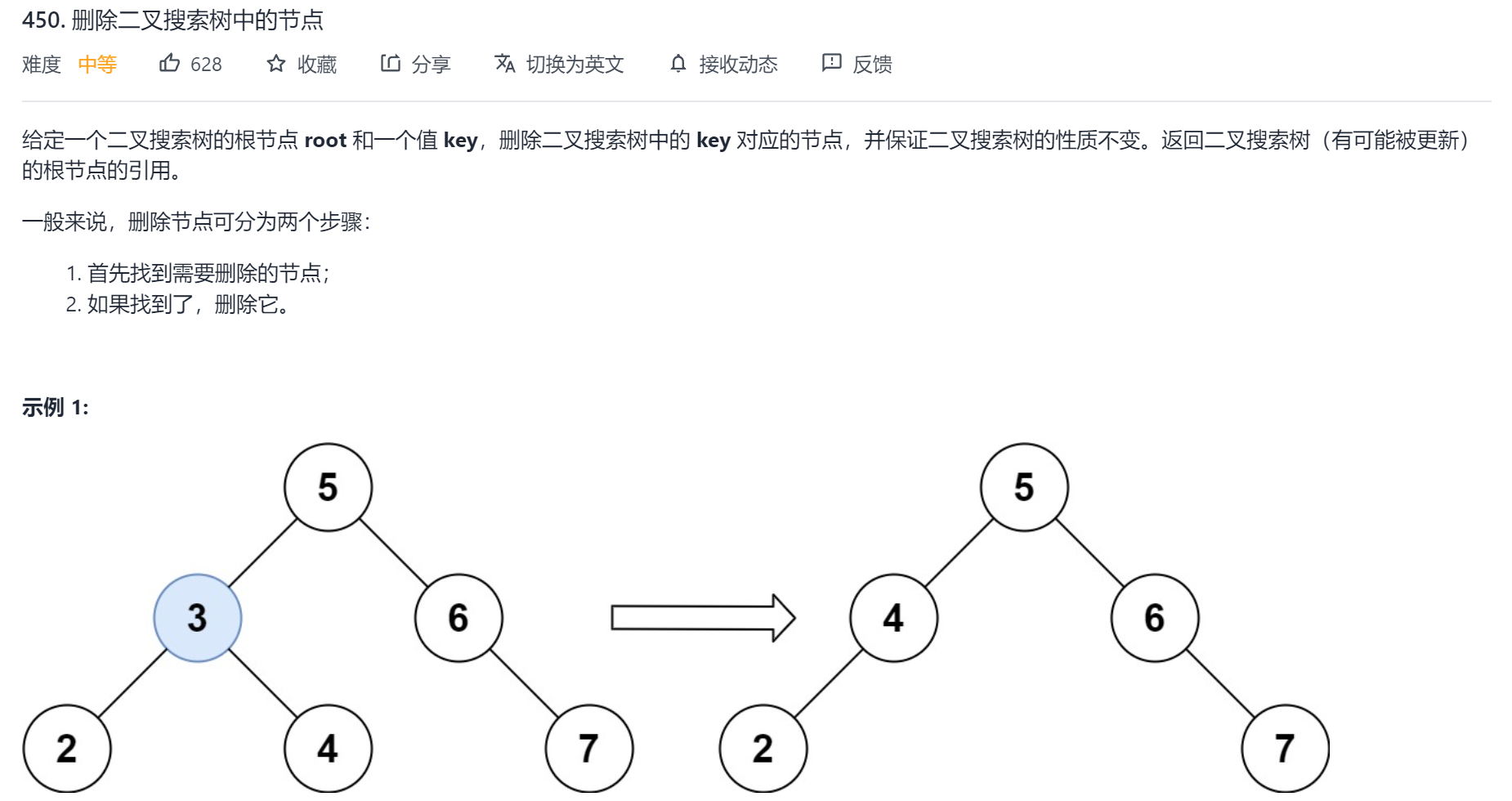
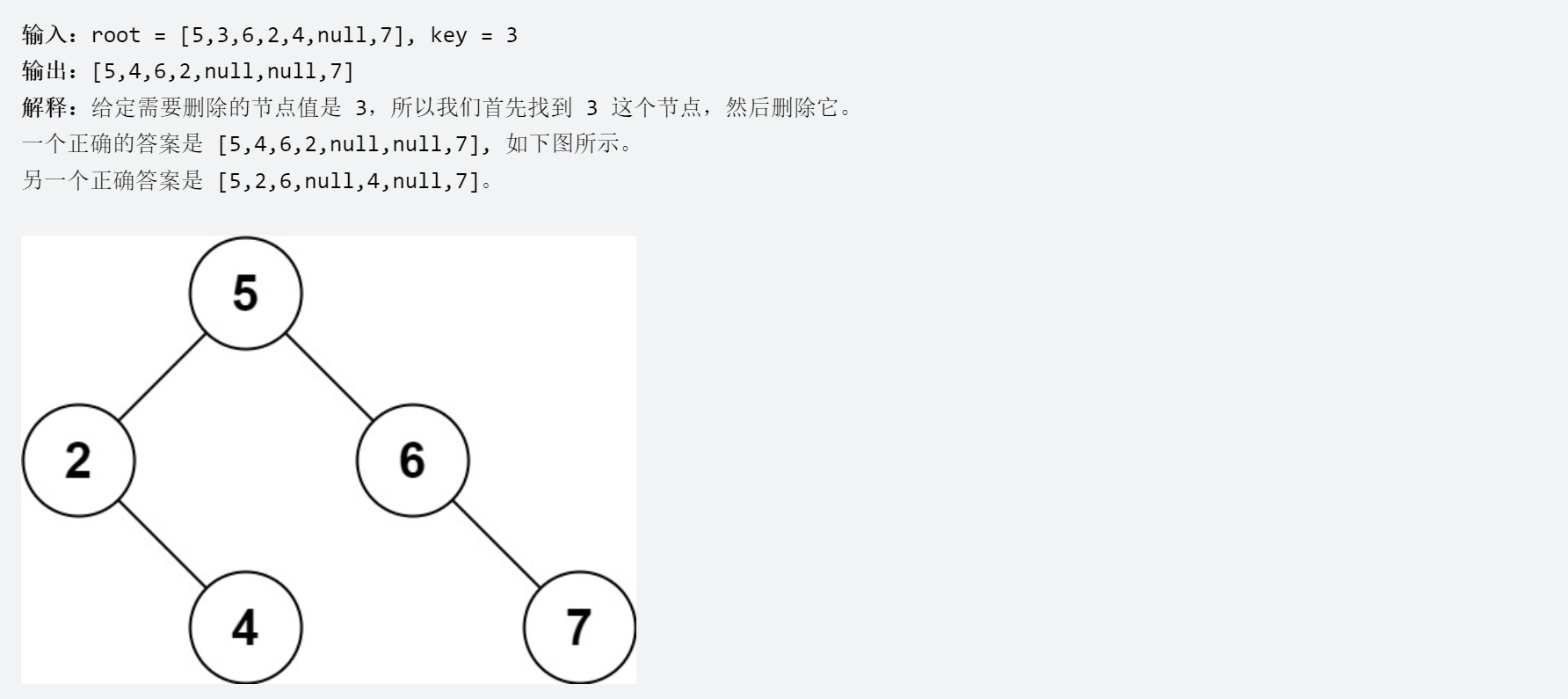
1.题目描述

原题链接：450. 删除二叉搜索树中的节点

2.解题思路

算法：递归

具体思路：

1. 如果key小于当前节点值，则递归左子树查找对应的key删除：dfs(root->left,key);
2. 如果key大于当前节点值，则递归右子树查找对应的key删除：dfs(root->right,key);
3. 如果key等于当前节点值，有分为以下几种情况： 1. 如果当前节点没有左子树也没有右子树则直接置为NULL，表示删除2. 如果当前节点有左子树没有右子树，则直接将当前节点置为左子树即可：root=root->right;3. 如果当前节点有右子树没有左子树，则直接将当前节点置为右子树即可：root=root->left;4. 如果当前节点既存在左子树又存在右子树，则递归遍历到右子树的最小值节点，将当前节点的值置为该最小值： root->val=t->val;，然后递归删除右子树的这个最小值节点：dfs(root->right,t->val);

3.代码

classSolution{public:TreeNode*deleteNode(TreeNode* root,int key){dfs(root,key);return root;}voiddfs(TreeNode*&root,int key){if(!root)return;if(key<root->val)dfs(root->left,key);elseif(key>root->val)dfs(root->right,key);else{if(!root->left&&!root->right) root=NULL;elseif(!root->left)  root=root->right;elseif(!root->right) root=root->left;else{
                auto t=root->right;while(t->left) t=t->left;
                root->val=t->val;dfs(root->right,t->val);}}}};