为梯度提升学习选择默认的特征编码策略需要考虑的两个重要因素是训练时间和与特征表示相关的预测性能。Automunge库是处理表格数据常用的库,它可以填充空值,也可以进行分类的编码和归一化等操作,默认的境况下Automunge对分类特征进行二值化处理,并对数值特征进行z-score归一化。本文将通过对一系列不同数据集进行基准测试来验证这些默认值是否是最优化的选项。
长期以来特征工程对深度学习应用的有用性一直被认为是一个已解决的否定问题,因为神经网络本身就是通用函数逼近器(Goodfellow et al., 2016)。但是即使在深度学习的背景下,表格特征也经常使用某种形式的编码进行预处理。Automunge (Teague, 2022a) 这个 python 库最初是为数字和分类特征的基本编码而构建的,例如 z-score 标准化和 one-hot 编码。在迭代开发过程中开始加入了完整的编码选项库,包括一系列数字和分类特征选项,现在也包括自动的规范化、二值化、散列和缺失数据填充场景。尽管这些编码选项可能对于深度学习来说是多余的,但这并不排除它们在其他模型中的效用,包括简单回归、支持向量机、决策树或本文的重点梯度提升模型。
本文目的是展示梯度提升模型下表格数据中的数字和分类特征的各种编码策略之间的基准测试研究的结果。
梯度提升
梯度提升 (Friedman, 2001) 是一种类似于随机森林 (Briemen, 2001) 的决策树学习范式 (Quinlan, 1986),通过递归训练迭代的目标以纠正前一次迭代的性能来提升优化模型。在实践中一般都会使用 XGBoost 库 (Chen & Guestrin, 2016) 和 LightGBM (Ke et al, 2017) 来进行建模。
到目前为止梯度提升还是被认为是 Kaggle 平台上表格模态竞赛的获胜解决方案,甚至在用于基于窗口的回归时,它的效率也在更复杂的应用(如时间序列顺序学习)中得到证明(Elsayed ,2022 ) .最近的表格基准测试论文中也说明,梯度提升可能仍然在大多数情况下胜过复杂的神经架构,如transformers (Gorishniy ,2021)。
传统观点认为,对于表格应用程序梯度提升模型具有比随机森林更好的性能,但在没有超参数调整的情况下会增加过度拟合的概率(Howard & Gugger,2020)。与随机森林相比,梯度提升对调整参数的敏感性更高,并且运行的参数数量更多,所以通常需要比简单的网格或随机搜索更复杂的调整。这样就出现了各种不同的超参数搜索的方法,例如一种可用的折衷方法是通过不同的参数子集进行顺序网格搜索(Jain,2016 ), Optuna 等黑盒优化库(Akiba ,2019 年)可以使用更自动化甚至并行化的方法进行超参数的搜索,这也是行业研究的一个活跃的方向。
特征编码
特征编码是指用于为机器学习准备数据的特征集转换。特征编码准备的常见形式包括数字特征标准化和分类特征的编码,尽管一些学习库(catboost)可能接受字符串表示中的分类特征并进行内部编码,但是手动的进行分类特征的转换还是有必要的。在深度学习出现之前,通常使用提取信息的替代表示来补充特征或以某种方式进行特征的组合来进行特征的扩充,这种特征工程对于梯度提升学习来说还是可以继续使用的。所以本文的这些基准的目的之一是评估实践与直接对数据进行训练相比的好处。
特征编码的一个重要问题就是需要领域知识,例如基于填充数值分布派生的 bin 与基于外部数据库查找提取 bin 来补充特征之间是否有很大的区别?在 Automunge 的情况下,内部编码库的编码基于固有的数字或字符串属性,并且不考虑可以根据相关应用程序域推断出的相邻属性。(日期时间格式的功能例外,它在自动化下自动提取工作日、营业时间、节假日等,并根据不同时间尺度的循环周期对条目进行冗余编码)
数字特征
数值标准化在实践中最常被使用的,例如z-score。在实践中可能发现的其他变化包括mean scaling 和max scaling 。更复杂的约定可以转换除尺度之外的分布形状,例如 box-cox 幂律变换(Box & Cox, 1964) 或Scikit-Learn 的分位数转换器qttf(Pedregosa ,2011),都可以将特征转换成一个更像高斯分布的特性集。数字归一化更常用于线性模型,而不是树的模型,例如在神经网络中,它们的目的是跨特征进行归一化梯度更新,应用于数值特征的标准化类型似乎会影响性能。
分类特征
分类编码通常在实践中使用独热编码进行转换,这种热编码的做法在高基数情况下存在缺陷(分类很多导致生成的特征多并且离散),梯度提升模型中分类标签过多时甚至可能导致训练超过内存限制。Automunge 库试图以两种方式规避这种高基数边缘情况,首先是默认使用二值化编码而不是独热编码,其次是通过区分哈希编码的最高基数集(Teague,2020a),减少唯一条目的数量。
分类二值化是可以理解为将模拟信号转换成数字信号过程中的量化,返回特征中每一个byte位代表是否属于该类
分类表示的第三种常见编码方式是标签编码,他将分类表示为一个连续的数值型变量。
基准基准
本文的基准测试是通过训练时间和模型性能这两个关键性能指标来评估一系列数字和分类编码场景。在配备 AMD 3970X 处理器、128Gb RAM 和两个 Nvidia 3080 GPU 的 Lambda 工作站上进行了约 1.5 周的测试。训练是通过 Optuna 调整的 XGBoost 进行的,具有 5-fold快速交叉验证 (Swersky et al, 2013) 和 如果33 次调整迭代没有改进则停止训练。性能指标是对25% 验证集进行根据 f1 分数评估进行的。
以上是对分类任务的偏差和方差性能进行平衡评估的良好默认设置(Stevens ,2020 )。在来自 OpenML 基准测试库(Vanschoren ,2013)的 31 个表格分类数据集上循环 5 次并取平均值。报告的指标是上面说提到的每种编码类型的 31 个数据集的 5 次重复的平均值,这些编码类型都使用了所有用于训练的数字或分类特征。
数字特征的结果如下:

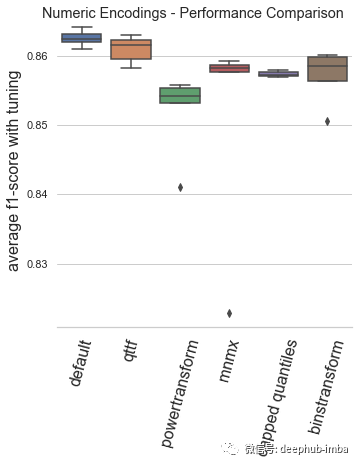
最终模型表现:
default:Automunge 的默认值使用 z 分数规范化(库中的“nmbr”代码)从调整持续时间和模型性能的角度来看,默认编码已被验证为平均表现最佳的场景。
qttf:具有正态输出分布的 Scikit-Learn QuantileTransformer,分位数分布转换的平均表现不如简单的 z 分数归一化,尽管它仍然是表现最好的。
powertransform:根据分布属性在“bxcx”、“mmmx”或“MAD3”之间有条件地编码(通过Automunge 库的 powertransform = True 设置),这是效果最差的场景。
mmmx:min max scaling 'mnmx' 将特征分布转移到 0-1 范围内,这种情况的表现比 z-score 归一化差得多,这可能是由于异常值导致数据在编码空间中“挤在一起”的情况。
capped quantiles:min max scaling with capped outliers at 0.99 and 0.01 quantiles ('mnm3' code in library),这种情况最好直接与mmmx进行比较,表明了默认设置异常值上限并不能提高平均性能。
binstransform:z-score 归一化再加上以 5 个独热编码标准偏差箱(通过库的 binstransform = True 设置),这个配置除了增加了训练时间以外,似乎对模型性能没有好处。
分类特征的结果如下:


default:Automunge 的默认值是分类二值化(库中的“1010”代码),从调整持续时间和模型性能的角度来看,默认编码已被验证为最好的。
onht:独热编码,这通常用作主流实践中的默认值,与二值化相比,模型性能影响出人意料地不好。基于这个测试,建议在特殊用例之外(例如,出于特征重要性分析的目的)停止使用 one-hot 编码。
ord3:具有按分类频率“ord3”排序的整数的序数编码,按类别频率而不是字母顺序对序数整数进行排序显着有益于模型性能,在大多数情况下,表现比独热编码好,但是仍然不如二值化。
ordl:“ordl”按字母顺序排序的整数的序数编码,字母排序的序数编码(Scikit-Learn 的 OrdinalEncoder 的默认值)表现不佳,建议在应用序数时默认为频率排序的整数。
hsh2:散列序号编码(高基数类别“hsh2”的库默认值),该基准主要用于参考,由于某些类别可能会合并,因此会对低基数集产生性能影响。
or19:多层字符串解析“or19”(Teague,2020b),多层字符串解析成功地超越了单热编码,并且是第二好的表现,但与普通二值化相比,它的性能不足以推荐默认值。如果应用程序可能具有与语法内容相关的某些扩展结构的情况下可以试试
总结
从训练时间和模型性能的角度来看, Automunge 库的 z-score 归一化和分类二值化在测试中都表现了出了很好的效果,所以如果你在处理表格数据的时候可以优先使用 Automunge 的默认值进行特征的处理,如果你想自己处理特征,那么z-score 归一化和分类二值化也是首先可以考虑的方法。
基准测试包括以下表格数据集,此处显示了它们的 OpenML ID 号:
- Click prediction / 233146
- C.C.FraudD. / 233143
- sylvine / 233135
- jasmine / 233134
- fabert / 233133
- APSFailure / 233130
- MiniBooNE / 233126
- volkert / 233124
- jannis / 233123
- numerai28.6 / 233120
- Jungle-Chess-2pcs / 233119
- segment / 233117
- car / 233116
- Australian / 233115
- higgs / 233114
- shuttle / 233113
- connect-4 / 233112
- bank-marketing / 233110
- blood-transfusion / 233109
- nomao / 233107
- ldpa / 233106
- skin-segmentation / 233104
- phoneme / 233103
- walking-activity / 233102
- adult / 233099
- kc1 / 233096
- vehicle / 233094
- credit-g / 233088
- mfeat-factors / 233093
- arrhythmia / 233092
- kr-vs-kp / 233091
引用
Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In KDD. (2019). URL https://optuna.org/#paper.
Box, G. E. P., and Cox, D. R. An analysis of transformations. Journal of the Royal Statistical Society: Series B (Methodological), 26(2):211–243, (1964). https://www.jstor.org/stable/2984418.
Breiman, L. Random Forests. Machine Learning45, 5–32 (2001). https://doi.org/10.1023/A:1010933404324.
Chen, T. and Guestrin, C., XGBoost: A Scalable Tree Boosting System. (2016). https://arxiv.org/abs/1603.02754.
Elsayed, S., Thyssens, D., Rashed, A., Samer Jomaa, H., and Schmidt-Thieme, L., Do We Really Need Deep Learning Models for Time Series Forecasting? (2021). https://arxiv.org/abs/2101.02118.
Friedman, J. H. Greedy function approximation: A gradient boosting machine. The Annals of Statistics, 29(5) 1189–1232 (October 2001). https://doi.org/10.1214/aos/1013203451.
Goodfellow, I. J., Bengio, Y., and Courville, A. Deep Learning. MIT Press, Cambridge, MA, USA, (2016). http://www.deeplearningbook.org.
Gorishniy, Y., Rubachev, I., Khrulkov, V., and Babenko, A., Revisiting Deep Learning Models for Tabular Data.Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc. (2021). URL https://openreview.net/forum?id=i_Q1yrOegLY.
Howard, J. and Gugger, S. Deep Learning for Coders with fastai and PyTorch. O’Reilly Media, 2020. https://www.oreilly.com/library/view/deep-learning-for/9781492045519/.
Jain, A. Complete Guide to Parameter Tuning in XGBoost with codes in Python.Analytics Vidhya (2016). https://www.analyticsvidhya.com/blog/2016/03/complete-guide-parameter-tuning-xgboost-with-codes-python/.
Kadra, A., Lindauer, M., Hutter, F., and Grabocka, J. Well-tuned simple nets excel on tabular datasets. In Beygelzimer, A., Dauphin, Y., Liang, P., and Vaughan, J. W. (eds.), Advances in Neural Information Processing Systems, 2021. URL https://openreview.net/forum?id=d3k38LTDCyO.
Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., Ye, Q., and Liu, T. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc. (2020). URL https://proceedings.neurips.cc/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf.
London, I. Encoding cyclical continuous features — 24-hour time. (2016) URL https://ianlondon.github.io/blog/encoding-cyclical-features-24hour-time/
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., Duchesnay, E., Scikit-learn: Machine Learning in Python, JMLR 12, pp. 2825–2830, (2011). https://www.jmlr.org/papers/v12/pedregosa11a.html.
Quinlan, J. R. Induction of Decision Trees. Mach. Learn. 1, 1, 81–106 (March 1986). https://doi.org/10.1023/A:1022643204877.
Ravi, Rakesh. One-Hot Encoding is making your Tree-Based Ensembles worse, here’s why?Towards Data Science, (January 2019). https://towardsdatascience.com/one-hot-encoding-is-making-your-tree-based-ensembles-worse-heres-why-d64b282b5769.
Stevens, E., Antiga, L., Viehmann, T. Deep Learning with PyTorch. Manning Publications, (2020). https://www.manning.com/books/deep-learning-with-pytorch.
Swersky, K. and Snoek, J. and Adams, R. P., Multi-Task Bayesian Optimization. Advances in Neural Information Processing Systems, volume 26. Curran Associates, Inc. (2013). URL https://proceedings.neurips.cc/paper/2013/file/f33ba15effa5c10e873bf3842afb46a6-Paper.pdf.
Teague, N. Automunge code repository, documentation, and tutorials, (2022). URL https://github.com/Automunge/AutoMunge.
Teague, N. Custom Transformations with Automunge. (2021). URL https://medium.com/automunge/custom-transformations-with-automunge-ae694c635a7e
Teague, N. Hashed Categoric Encodings with Automunge (2020a) https://medium.com/automunge/hashed-categoric-encodings-with-automunge-92c0c4b7668c.
Teague, N. Parsed Categoric Encodings with Automunge. (2020b) https://medium.com/automunge/string-theory-acbd208eb8ca.
Vanschoren, J., van Rijn, J. N., Bischl, B., and Torgo, L. OpenML: networked science in machine learning. SIGKDD Explorations 15(2), pp 49–60, (2013). https://arxiv.org/abs/1407.7722
作者:Nicholas Teague