吴恩达机器学习——第五周学习笔记

神经网络

代价函数（Cost Function）

正则化逻辑回归的代价函数：

神经网络的代价函数：

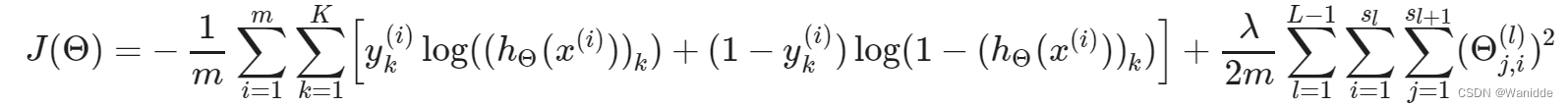
L：是神经网络架构的层数

Sl：l层的单元个数

K：输出单元的个数

sigmoid函数：

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

前向传播函数：

#前向传播函数
def forward_propogate(X, theta1, theta2):
    m = X.shape[0]  #m是X的行数
    
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)
    z2 = a1 * theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
    z3 = a2 * theta2.T
    h = sigmoid(z3)
    
    return a1, z2, a2, z3, h

前向传播的代价函数（含正则项）：

#带正则项的代价函数
def costReg(theta1, theta2, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    
    #计算前向传播参数
    a1, z2, a2, z3, h = forward_propogate(X, theta1, theta2)
    
    #使用公式计算代价函数
    J = 0
    for i in range(m):
        first = np.multiply(-y[i,:], np.log(h[i,:]))
        second = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first - second)
        
    J = J / m
    
    #加上正则项
    J += (float(learning_rate) / (2*m) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2))))
    
    return J

#对y标签进行编码 将y扩展成5000*10
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y)
y_onehot.shape

#变量初始化
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 1

#计算正则化的代价函数
costReg(theta1, theta2, input_size, hidden_size, num_labels, X, y_onehot, learning_rate)

反向传播算法（Backpropagation Algorithm）

前向传播：将训练集数据输入到神经网络的输入层，经过隐藏层，最后到达输出层并输出结果。

反向传播：由于神经网络的输入结果与输出结果有误差，则计算估计值与实际值之间的误差，并将

该误差从输出层向隐藏层反向传播，直至传播到输入层。

具体计算推导可以参考：​​​​​​反向传播计算推导

训练神经网络的具体步骤：

• 选择一个网络架构，选择神经网络的布局（包括每层有多少隐藏单元和总层数等等）
• 随机初始化权值θ
• 使用前向传播获取所有输入xi的输出h(xi)
• 计算代价函数
• 使用反向传播来计算偏导
• 使用梯度检测来确保反向传播的正常工作
• 最后使用梯度下降或者其他内置优化函数来最小化代价函数即min(J(θ))

Sigmoid函数的梯度（Sigmoid gradient）

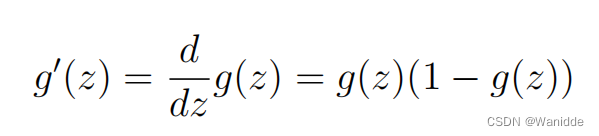
其中，sigmoid函数如下：

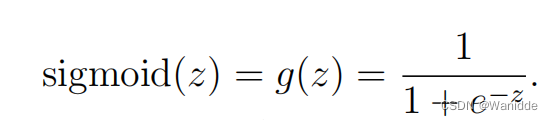
在绝对值比较大的数上，梯度应该接近0，当z=0时，梯度应该是0.25

#Sigmoid函数的梯度
def sigmoid_gradient(z):
    return np.multiply(sigmoid(z), (1-sigmoid(z)))

随机初始化（Random initialization）

当我们训练神经网络时，随机初始化对解决对称问题是很重要的。一种有效的策略就是随机的挑选一些θ值，使之均匀的落在{−ϵinit,ϵinit}。

np.random.random(size) 返回size大小的0-1的随机浮点数

计算

反向传播：给定训练集(x(t) , y(t))，先计算正向传播hΘ(x)，再对于第l层的每个节点j，计算误差项δj(l)，这个数据是衡量这个节点对最后输出的误差“贡献”了多少。
对于每个输出节点，我们可以直接计算输出值与目标值的差值，定义为δj(l)。对于每个隐藏节点，需要基于现有权重及(l+1)层的误差，计算δj(l)。

第l层的误差：

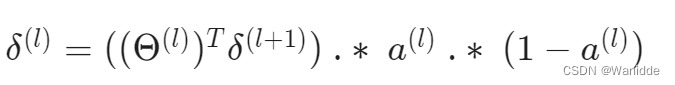
前向传播计算：

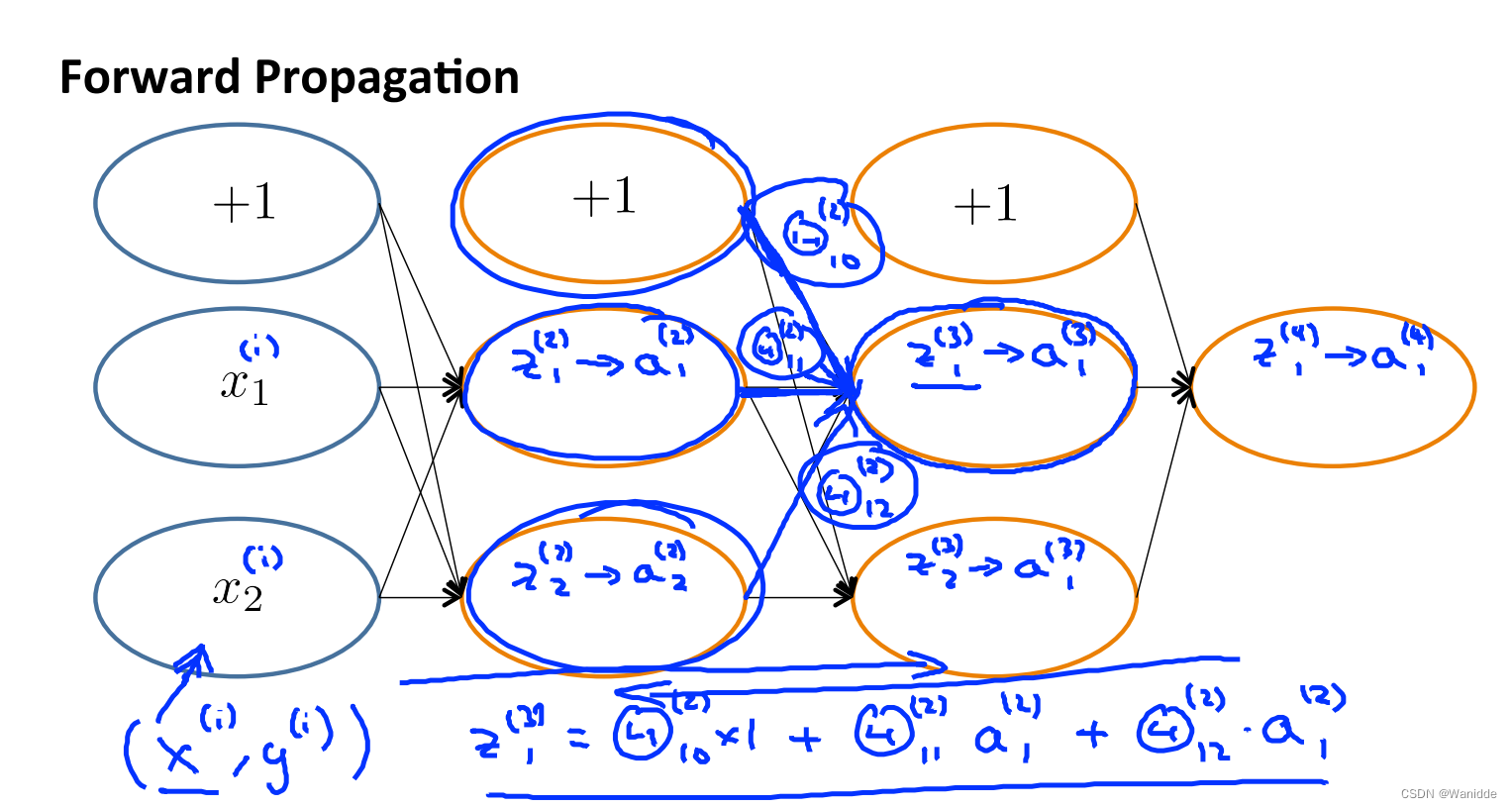
反向传播每层误差的计算：

代码：

#正则化的反向传播
def backpropReg(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    
    #参数数组重塑为每个层的参数矩阵
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size+1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size*(input_size+1):], (num_labels, (hidden_size + 1))))
    
    #计算前向传播参数
    a1, z2, a2, z3, h = forward_propogate(X, theta1, theta2)
    
    #初始化
    J = 0
    delta1 = np.zeros(theta1.shape)
    delta2 = np.zeros(theta2.shape)
    
    #计算代价函数
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    
    J = J / m
    
    #使用反向传播
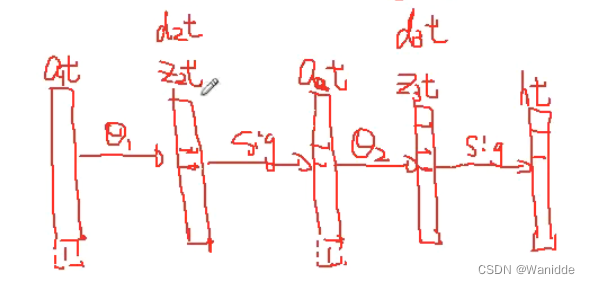
    for t in range(m):
        a1t = a1[t,:]
        z2t = z2[t,:]
        a2t = a2[t,:]
        ht = h[t,:]
        yt = y[t,:]
        
        d3t = ht - yt
        
        z2t = np.insert(z2t, 0, values=np.ones(1))
        d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t))
        
        delta1 = delta1 + (d2t[:,1:]).T * a1t
        delta2 = delta2 + d3t.T * a2t
        
    delta1 = delta1 / m
    delta2 = delta2 / m
    
    #加入正则项  [:,1:]去掉一维（偏置项）
    delta1[:,1:] = delta1[:,1:] + (theta1[:,1:] * learning_rate) / m
    delta2[:,1:] = delta2[:,1:] + (theta2[:,1:] * learning_rate) / m
    
    #将梯度矩阵分解成单个的数组
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
    
    return J, grad

梯度检测（Gradient Checking）

梯度检测是确保我们的反向传播按预期工作。将偏导近似等于：

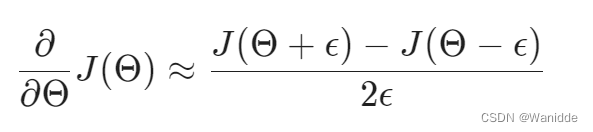
用图像表示如下，和微分的定义类似。

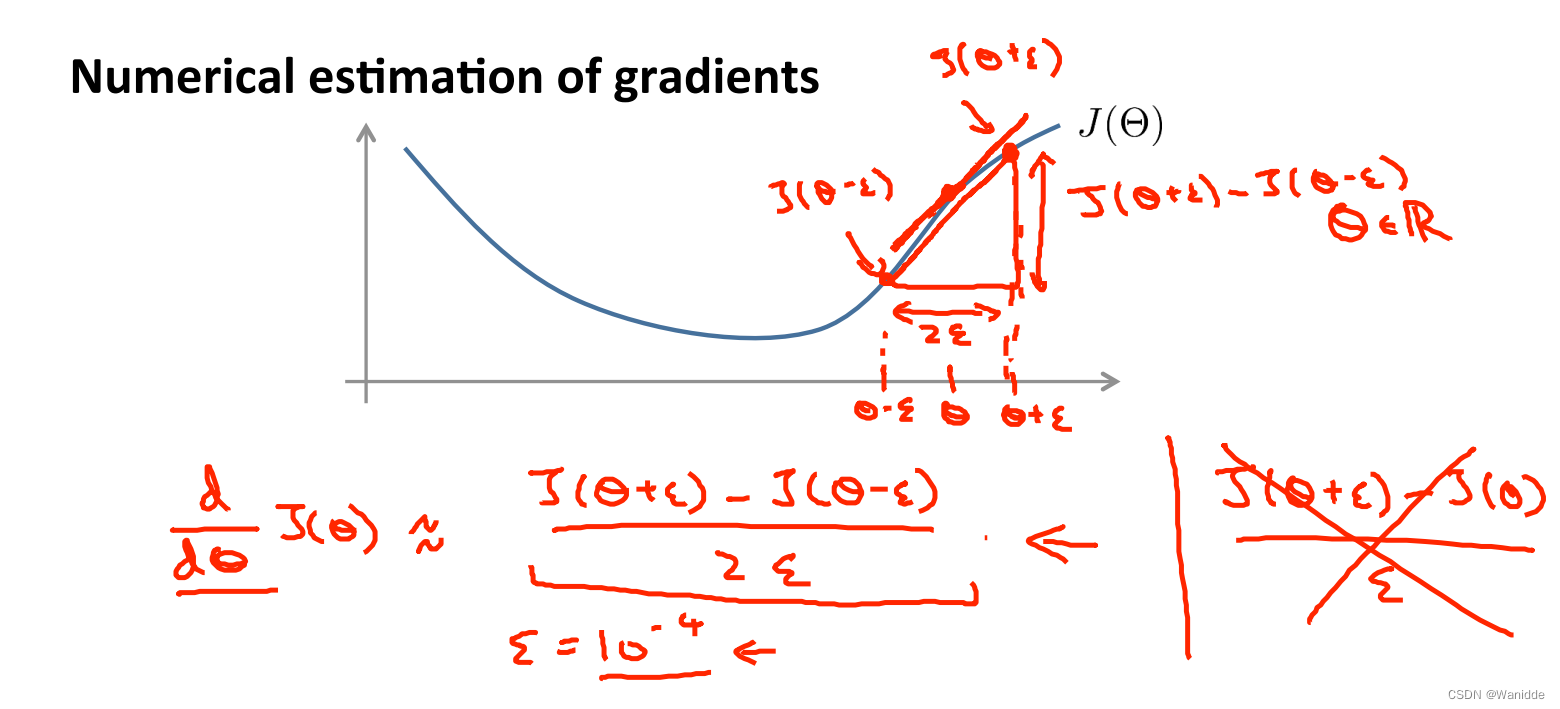
是一个很小的值，如

神经网络的执行情况如下：

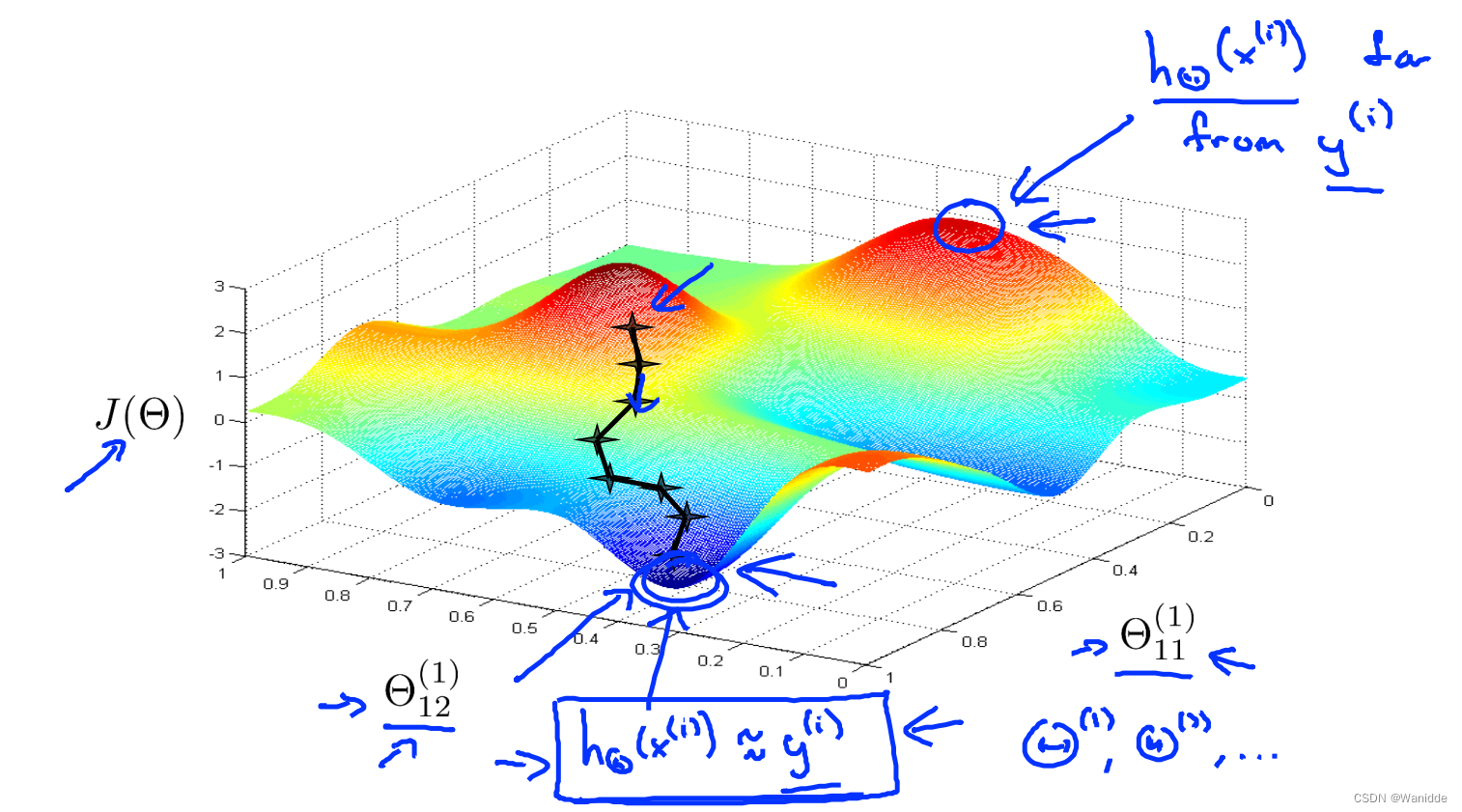
学习参考：吴恩达机器学习第五周