Self-attention 有一个进阶的版本,叫做 Multi-head Self-attention, Multi-head Self-attention,其实今天的使用是非常地广泛的 。
在LHY2021作业 4 裡面,助教原来的 code 4 有,Multi-head Self-attention,它的 head 的数目是设成 2,那刚才助教有给你提示说,把 head 的数目改少一点 改成 1,其实就可以过medium baseline
但并不代表所有的任务,都适合用比较少的 head,有一些任务,比如说翻译,比如说语音辨识,其实用比较多的 head,你反而可以得到比较好的结果至於需要用多少的 head,这个又是另外一个****hyperparameter,也是你需要调的那為什麼我们会需要比较多的 head 呢,你可以想成说相关这件事情我们在做这个 Self-attention的时候,我们就是用** q 去找相关的 k**,但是相关这件事情有很多种不同的形式,有很多种不同的定义,所以也许我们不能只有一个q,我们应该要有多个 q,不同的 q 负责不同种类的相关性
所以假设你要做 Multi-head Self-attention 的话,你会怎麼操作呢?
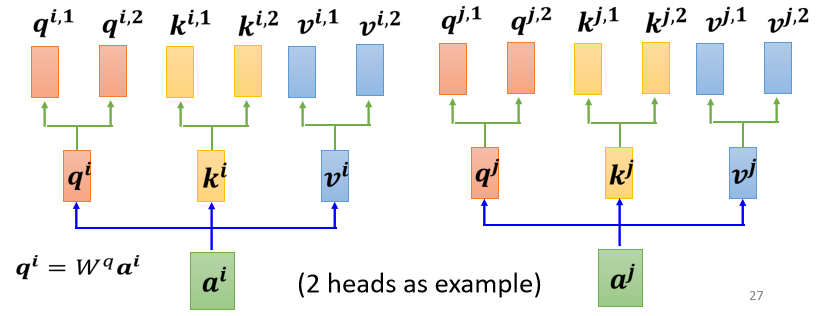
1.先把 a 乘上一个矩阵得到 q
2.再把 q 乘上另外两个矩阵,分别得到 跟
,那这边还有 这边是用两个上标,i 代表的是位置,然后这个 1 跟 2 代表是,这个位置的第几个 q,所以这边有
跟
,代表说我们有两个 head
我们认為这个问题,裡面有两种不同的相关性,是我们需要產生两种不同的 head,来找两种不同的相关性。既然 q 有两个,那 k 也就要有两个,那 v 也就要有两个,从 q 得到和
,从 k 得到
和
,从 v 得到 ,那其实就是把 q 把 k 把 v,分别乘上两个矩阵,得到这个不同的 head,就这样子而已,对另外一个位置,也做一样的事情。
只是现在,它在算这个 attention 的分数的时候,它就不要管那个
了
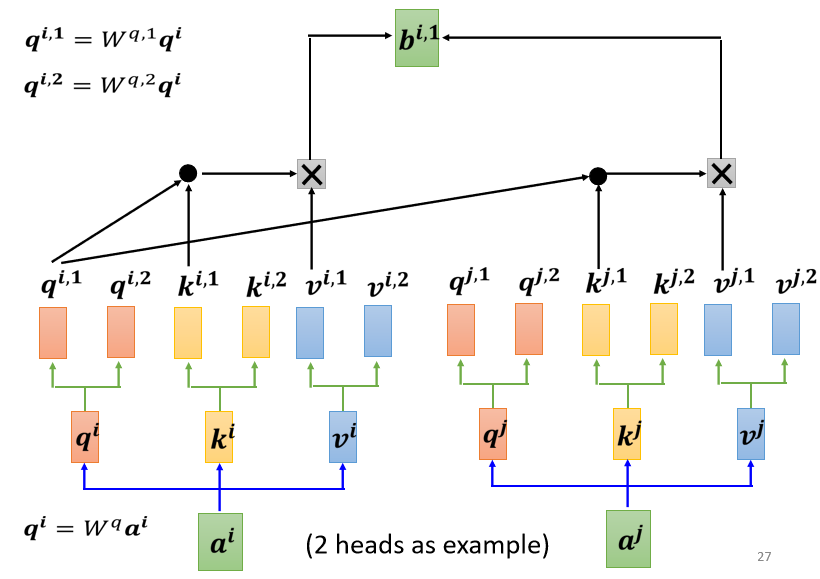
所以 就跟
算 attention
就跟算
attention,也就是算这个 dot product,然后得到这个 attention 的分数
然后今天在做 weighted sum 的时候,也不要管 了,看
就好,所以你把 attention 的分
数乘 ,把 attention 的分数乘
,然后接下来就得到
这边只用了其中一个 head,那你会用另外一个 head,也做一模一样的事情
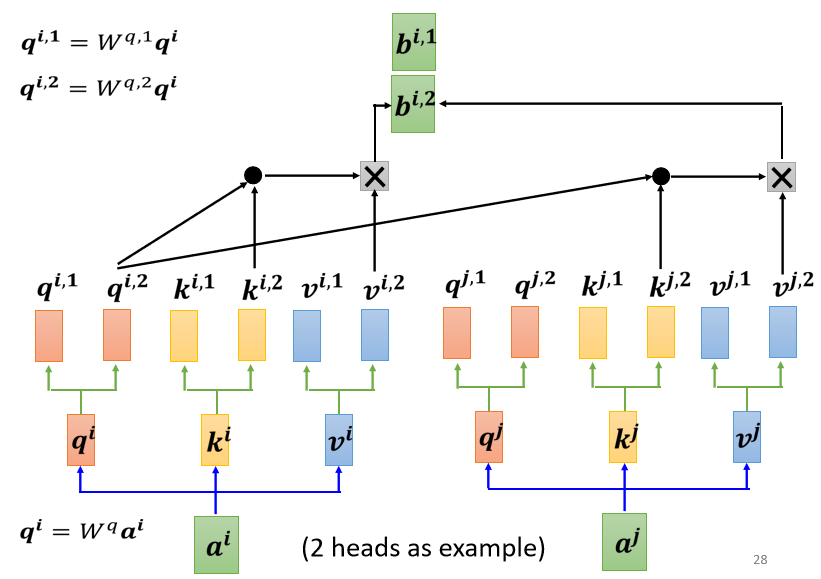
如果你有多个 head,有 8 个 head 有 16 个 head,那也是一样的操作,那这边是用两个 head 来当作例子,来给你看看有两个 head 的时候,是怎麼操作的,现在得到的bi1和bi2
然后接下来你可能会把 跟
,把它接起来,然后再通过一个 transform。
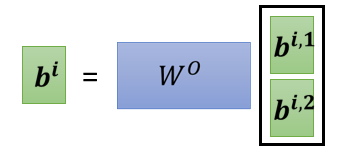
也就是再乘上一个矩阵,然后得到 bi,然后再送到下一层去,那这个就是 Multi-head attention,一个这个Self-attention 的变形
版权归原作者 Jc随便学学 所有, 如有侵权,请联系我们删除。