群智能概述
群(swarm):某种交互作用的组织或agent的结构集合。人们把群居昆虫的集体行为称作“群智能”,即低智能的主体通过合作表现出高智能行为的特性。
群智能算法是一种基于生物群体行为规律的计算技术。
粒子群优化
基本粒子群算法描述

粒子速度和位置的更新

流程图
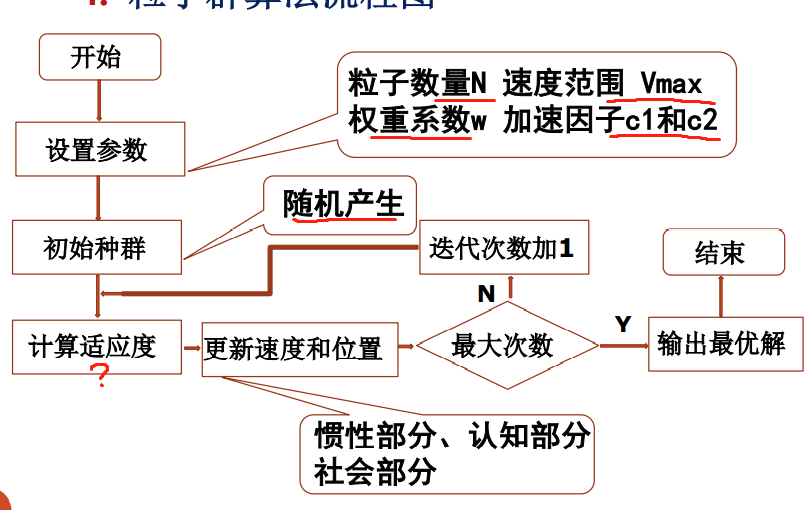
参数分析
惯性权重w
使粒子保持运动惯性,也表示微粒对当前自身运动状态的信任。较大的w有利于跳出局部极值,而较小的w有利于算法收敛。
改进的惯性权重w:随着迭代的进行,线性地减小w的值。
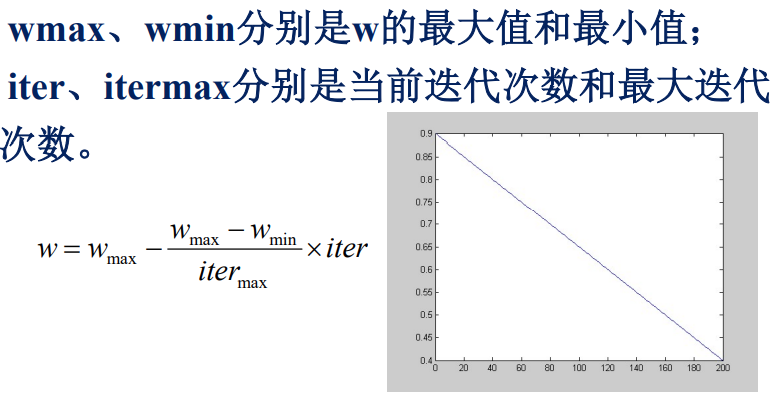
加速因子c1和c2
表示粒子的动作来源于自己经验的部分和其它粒子经验的部分。
改进的加速因子c1和c2
将c1和c2统一为一个控制参数,φ= c1+c2;
如果φ很小,微粒群运动轨迹将非常缓慢;如果φ很大,则微粒位置变化非常快;
当φ=4.0(c1=2.0,c2=2.0)时,具有很好的收敛效果。
粒子数
通常一般取20~40,对较难或特定类别的问 题可以取100~200。
最大速度vmax
决定粒子在一个循环中最大的移动距离,通常设定为粒子的范围宽度。
蚁群算法
以TSP问题为例说明蚁群算法。
设蚂蚁的数量为m,城市的数量为n,城市i和城市j的距离为距离选用欧式距离,t时刻城市i和城市j连接路径的信息素浓度为τ(i, j)
在算法初始时刻,设各城市连接路径的信息素浓度具有相同的值,m只蚂蚁放到n座城市。

α是信息素重要程度因子。β是启发函数重要程度因子。tabuk为禁忌表,表示已经访问的城市集合。
5.蚂蚁从当前城市访问下一城市的概率确定后,通常采用轮盘赌法选择下一城市,概率大被选中机会就大。
6.当所有蚂蚁完成一次访问后,各路径上的信息素将进行更新,信息素公式更新如下

7.针对蚂蚁释放信息素问题有如下三种模型
这三种模型分别对应路径的整体信息(蚂蚁所访问路径的总长)、局部信息(蚂蚁所访问城市间的距离)和不考虑路径信息。
8.以下优化TSP问题,选用ant cycle system模型, 即路径的整体信息路径越短,释放的信息素度越高。
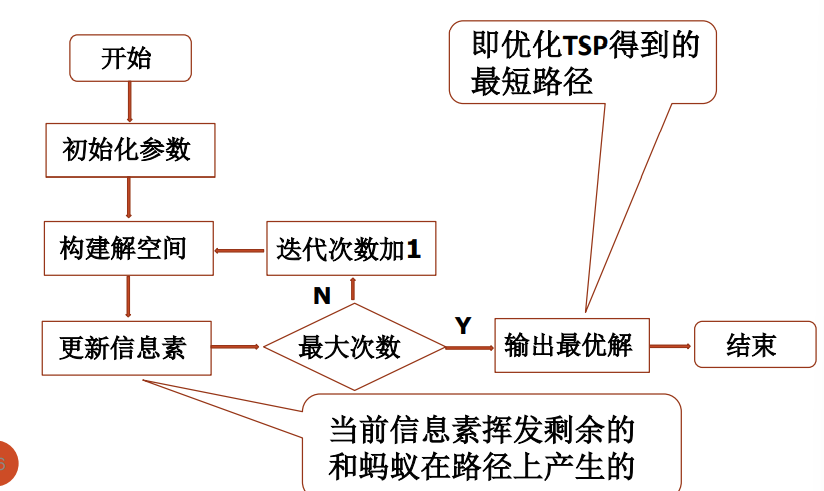
蚁群算法的改进
- 最优解保留策略(Ant System with Elitist)能够以更快的速度获得最好解,但是如果选择的精英过多则算法会由于较早收敛于局部次优解而导致搜索的过早停滞。
- 局部信息素更新使已选的路径对后来的蚂蚁具有较小的影响力,从而使蚂蚁对没有选中的路径有更强的探索能力。
- 最大–最小蚂蚁系统(max-min ant system)每次迭代后,只有最优解(最优蚂蚁)所属路径上的信息被更新;为了避免过早收敛,将各条路径可能的信息素限制于[τmin ,τmax];在算法初始时刻,ρ取较小值,算法有更好的发现较好解的能力。 随着迭代次数的增加, ρ变大加快算法的收敛。
版权归原作者 我飘向北方 所有, 如有侵权,请联系我们删除。


