二叉树的链式结构(C语言版)

攀登顶峰，这种奋斗的本身就足以充实人的心。

文章目录

💒1.前言

以前我们学习顺序表、链表和堆时，一上来就是学习它们的增删查改等接口函数，但是普通的链式二叉树的增删查改没有意义。如果是为了单纯存储数据，不如使用线性表。我们学习链式二叉树是为了更好地控制它的结构，为后续学习更复杂的搜索二叉树打基础，而且很多二叉树oj算法题都出在普通二叉树上。

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

#include<stdio.h>#include<stdlib.h>#include<assert.h>typedefint BTDataType;typedefstructBinaryTreeNode{structBinaryTreeNode* left;structBinaryTreeNode* right;
    BTDataType data;}BTNode;

BTNode*BuyBTNode(BTDataType x){
    BTNode* node =(BTNode*)malloc(sizeof(BTNode));if(node ==NULL){printf("malloc fail\n");exit(-1);}

    node->data = x;
    node->left = node->right =NULL;return node;}

BTNode*CreatBinaryTree(){
    BTNode* node1 =BuyBTNode(1);
    BTNode* node2 =BuyBTNode(2);
    BTNode* node3 =BuyBTNode(3);
    BTNode* node4 =BuyBTNode(4);
    BTNode* node5 =BuyBTNode(5);
    BTNode* node6 =BuyBTNode(6);

    node1->left = node2;
    node1->right = node4;
    node2->left = node3;
    node4->left = node5;
    node4->right = node6;return node1;}

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树
2. 非空：根节点，根节点的左子树、根节点的右子树组成的 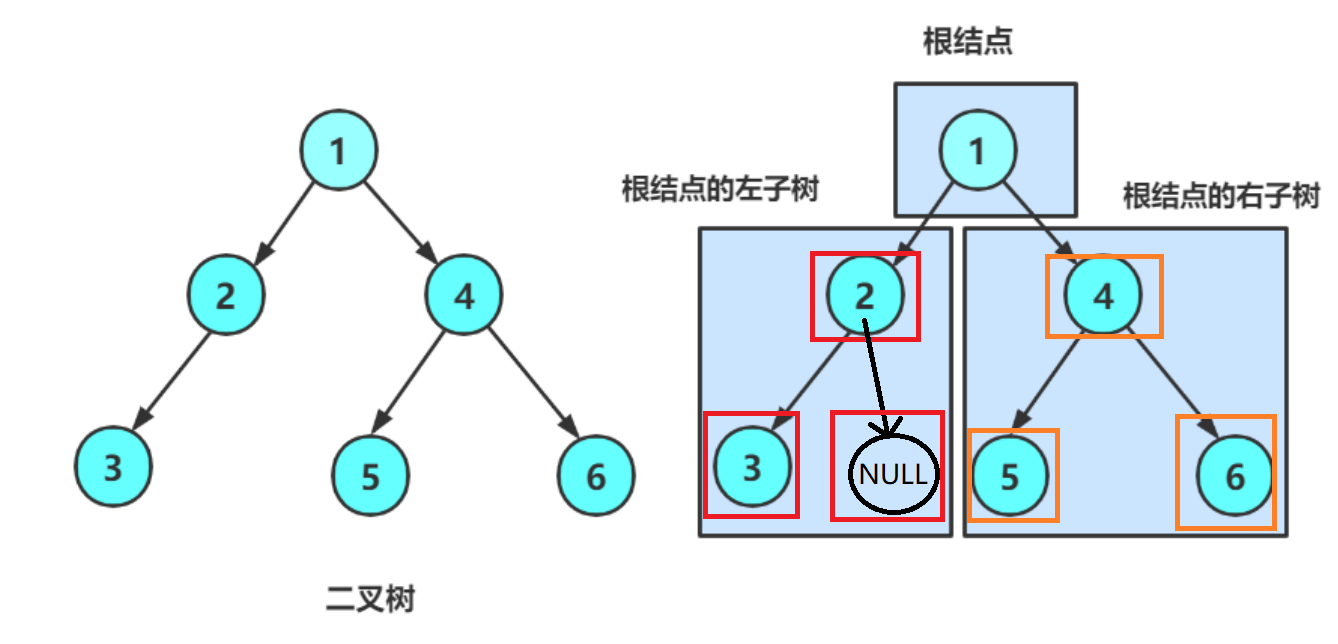从图中可以看出根节点的左子树和右子树又可以被分为根、根的左子树、根的右子树。因此二叉树定义是递归式的，后序基本操作中基本都是按照该概念实现的。

🌟2二叉树的遍历

🌻2.1 前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Rightsubtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。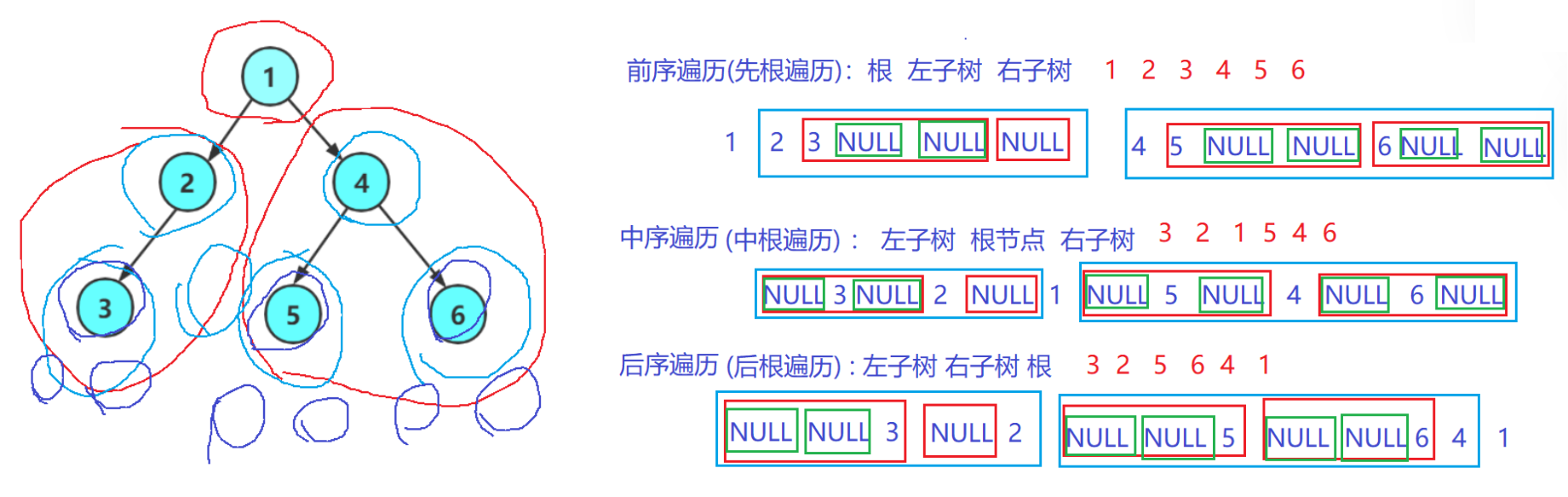

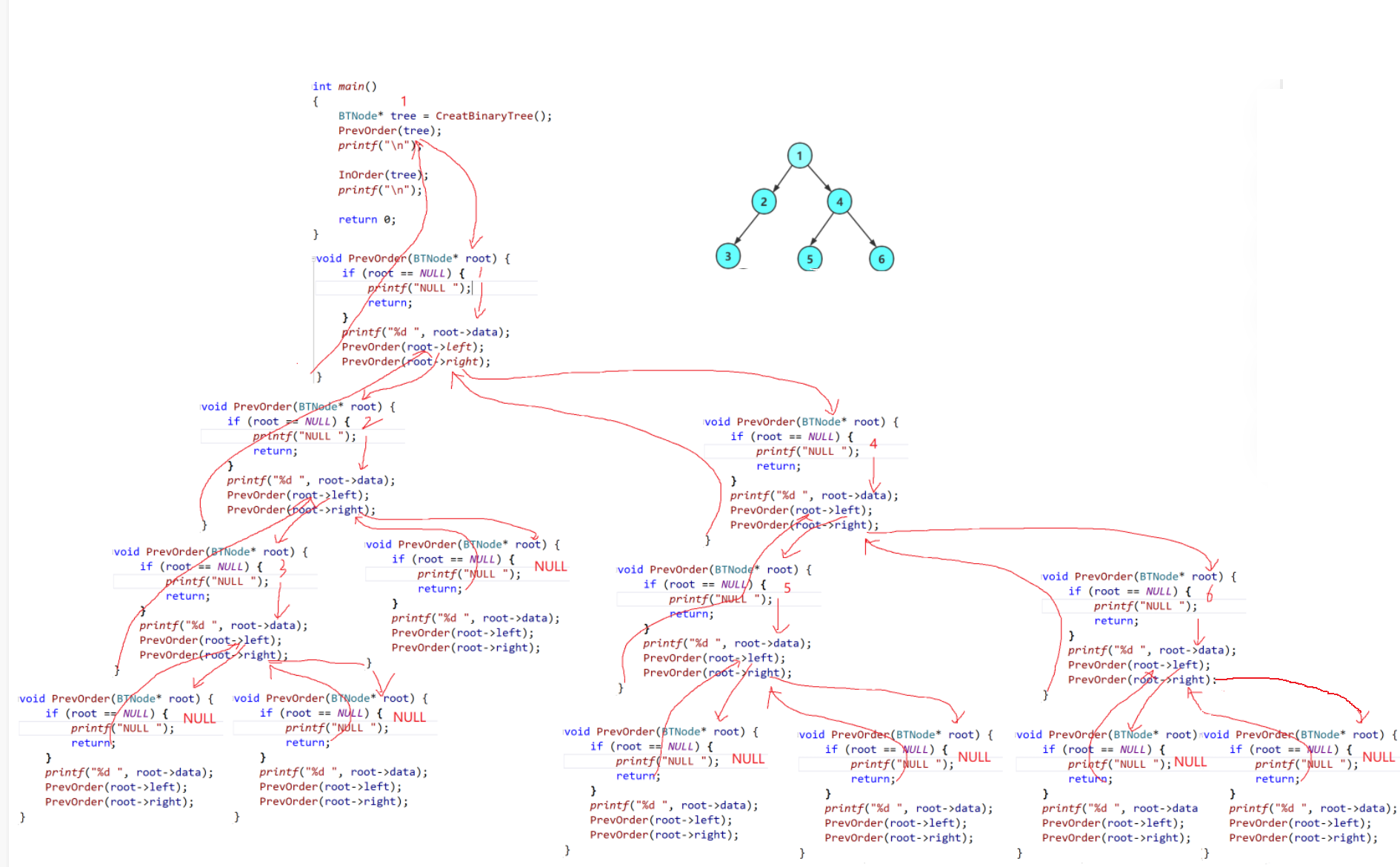
🍅2.2 前序代码演示及递归图解

voidPrevOrder(BTNode* root){if(root ==NULL){printf("NULL ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);}

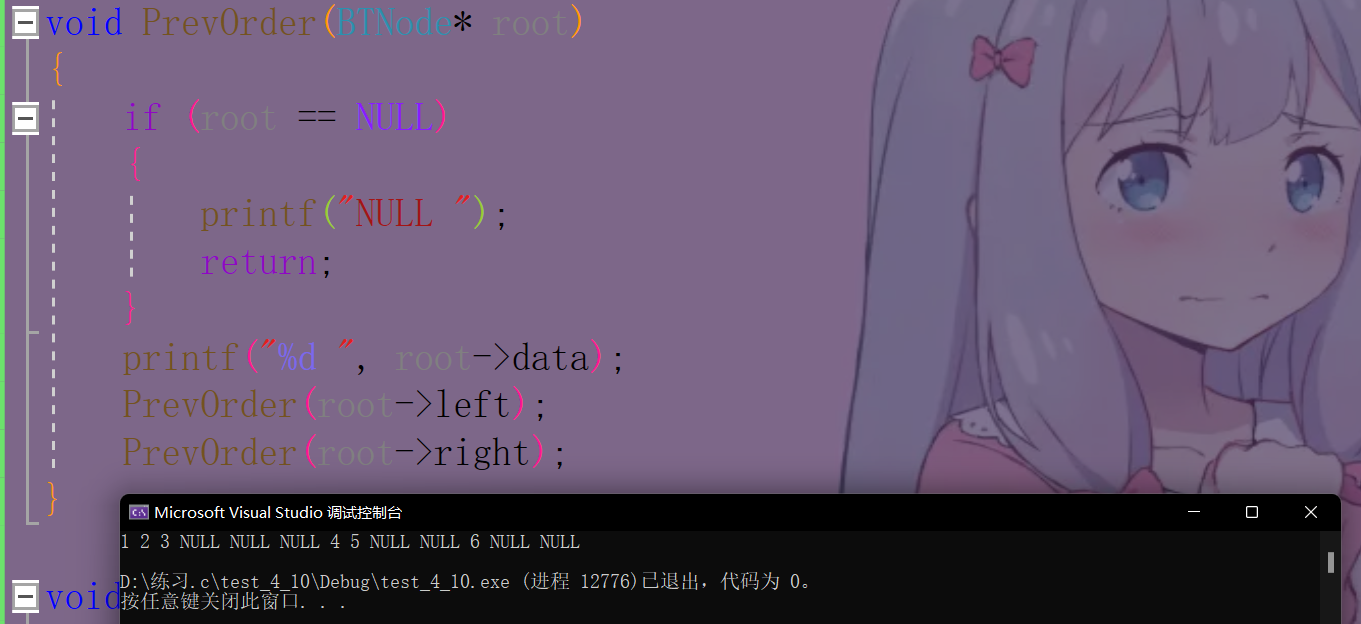
🍆2.3 中序代码演示及递归图解

voidInOrder(BTNode* root){if(root ==NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);}

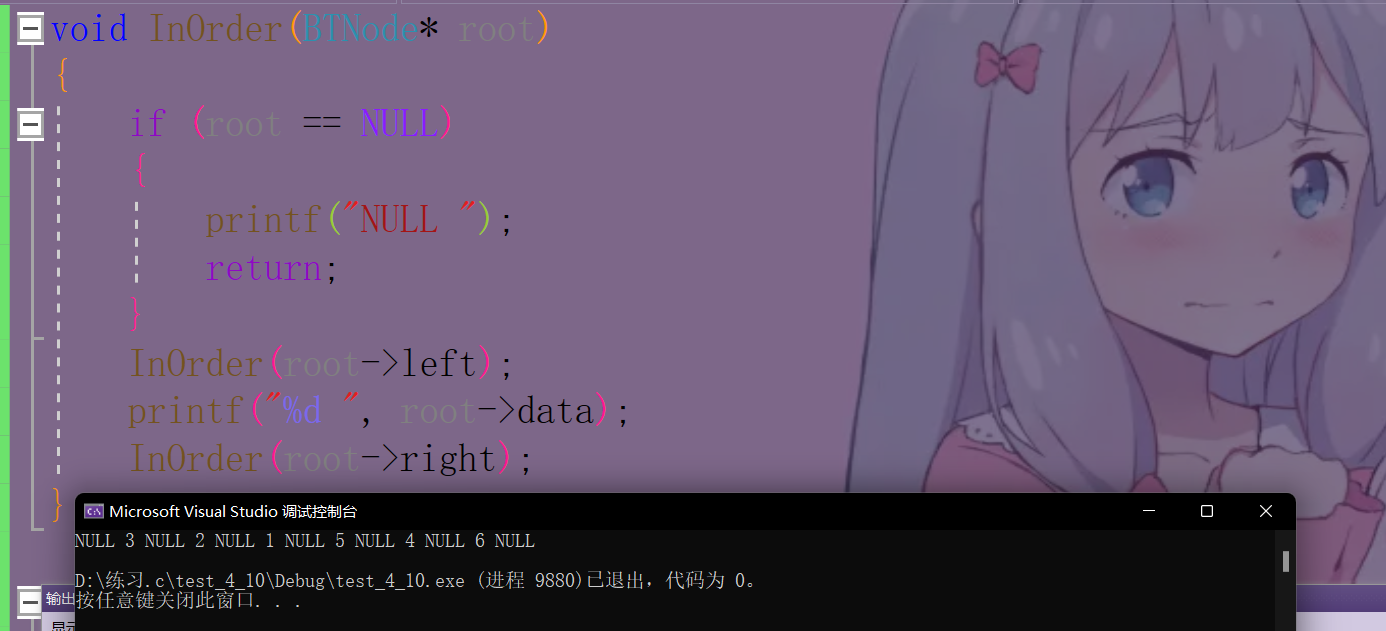
🍇2.4 后序代码演示及递归图解

voidPostOrder(BTNode* root){if(root ==NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);}

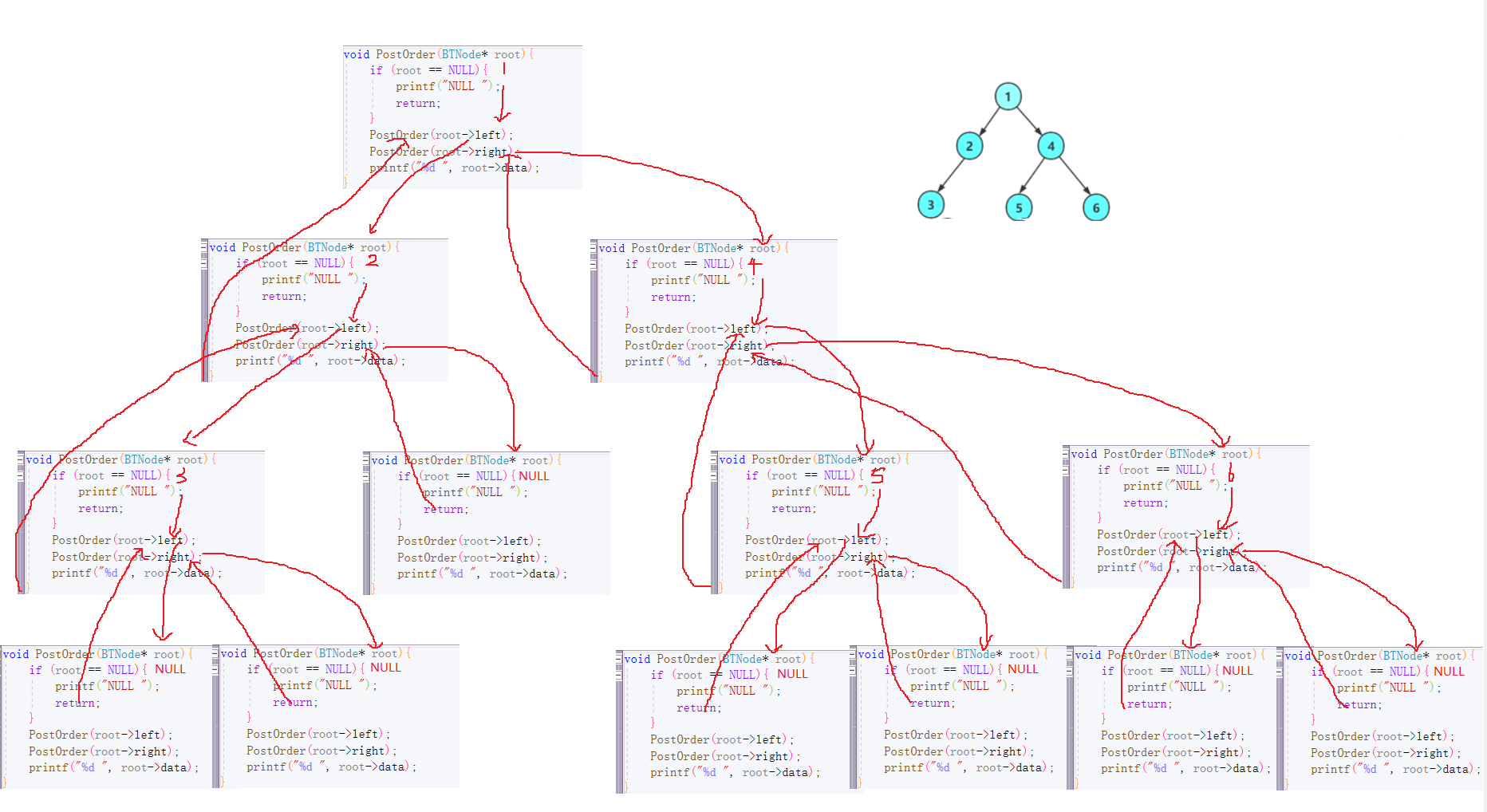
🍈2.5 层序遍历

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
思路：

1. 创建一个指针数组，保存二叉树结构体指针，
2. 保存二叉树根节点，再申请变量 in、out ，控制数组，在遍历过程中，始终能找到节点和该节点的前一个节点，
3. 循环以上过程。

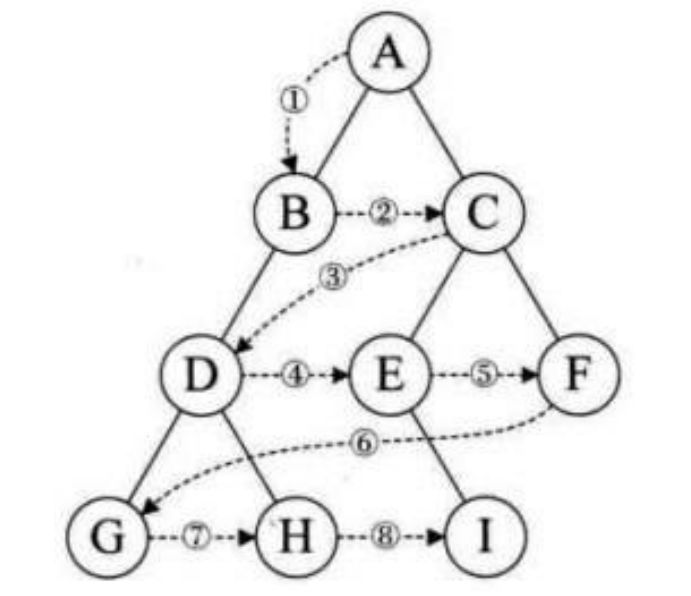
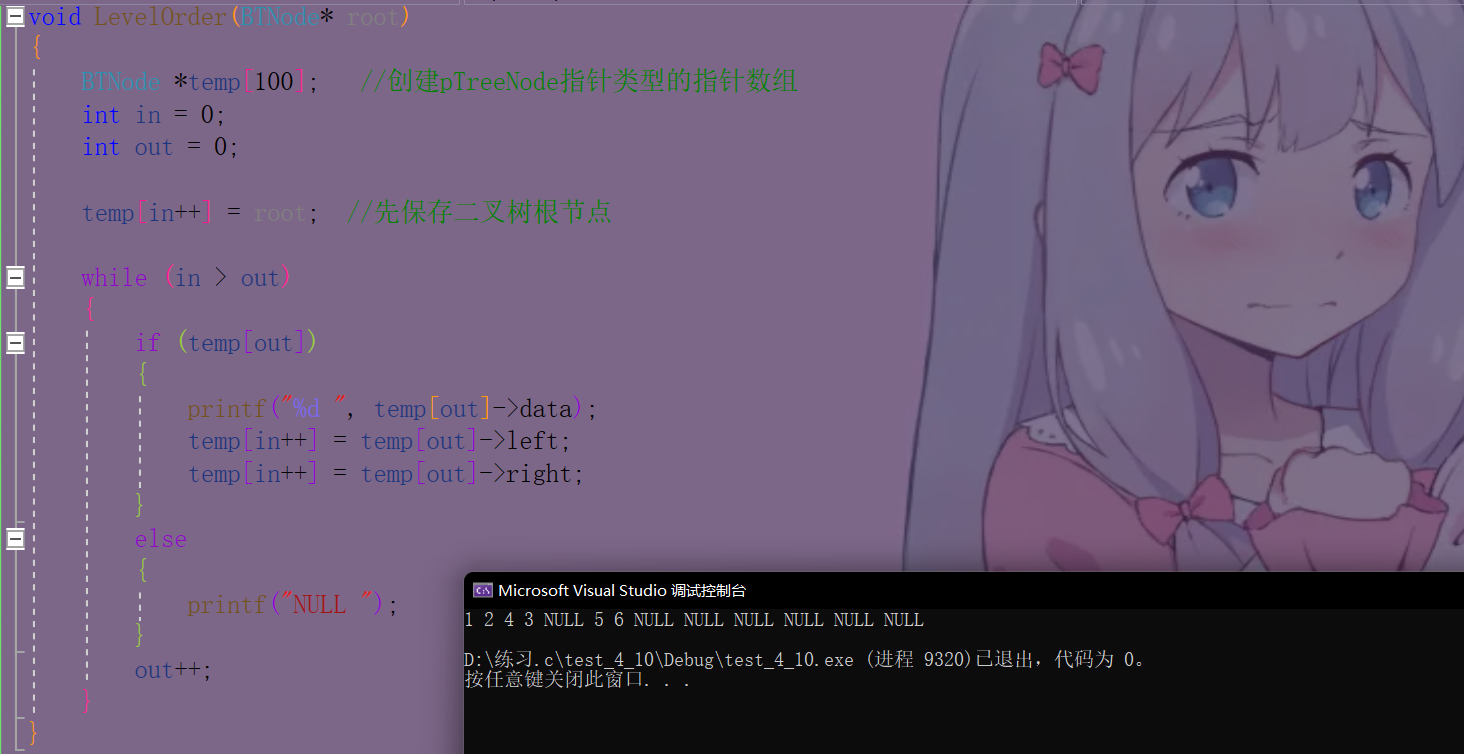
// 层序遍历voidLevelOrder(BTNode* root){
    BTNode *temp[100];//创建pTreeNode指针类型的指针数组int in =0;int out =0;

    temp[in++]= root;//先保存二叉树根节点 while(in > out){if(temp[out]){printf("%d ", temp[out]->data);
            temp[in++]= temp[out]->left;
            temp[in++]= temp[out]->right;}else{printf("NULL ");}
        out++;}}

🌺3 节点个数以及高度等

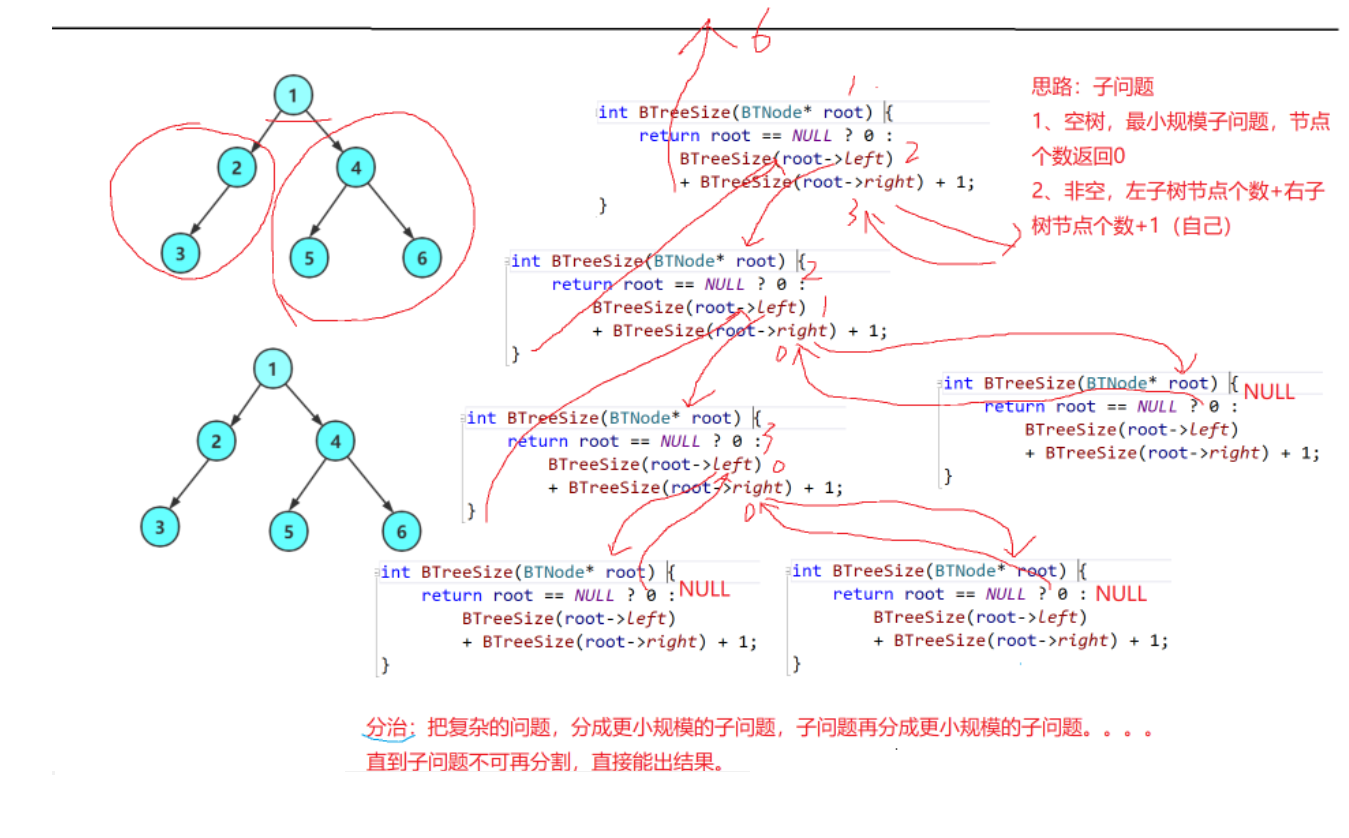
🍍3.1 节点个数及递归图解

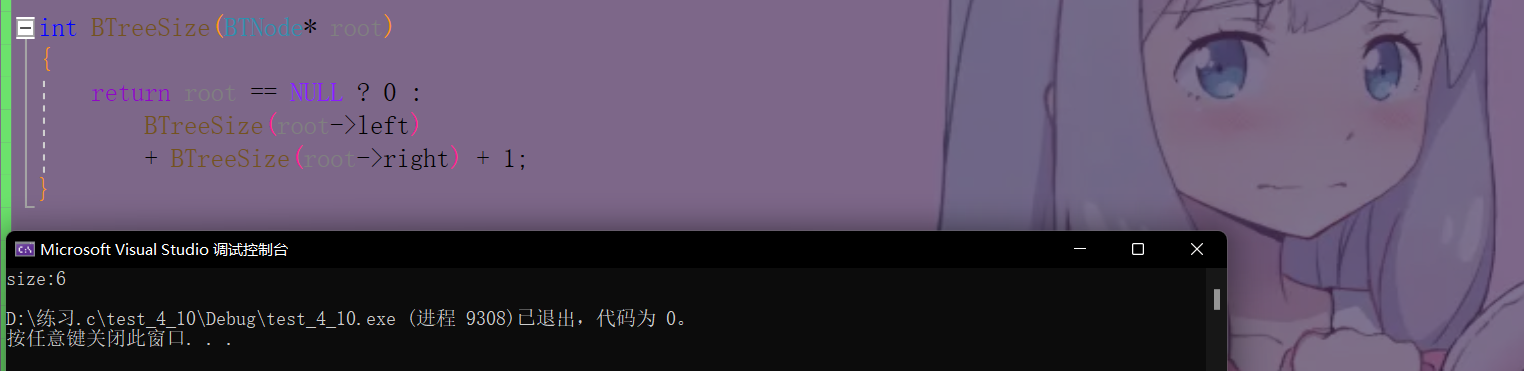
intBTreeSize(BTNode* root){return root ==NULL?0:BTreeSize(root->left)+BTreeSize(root->right)+1;}

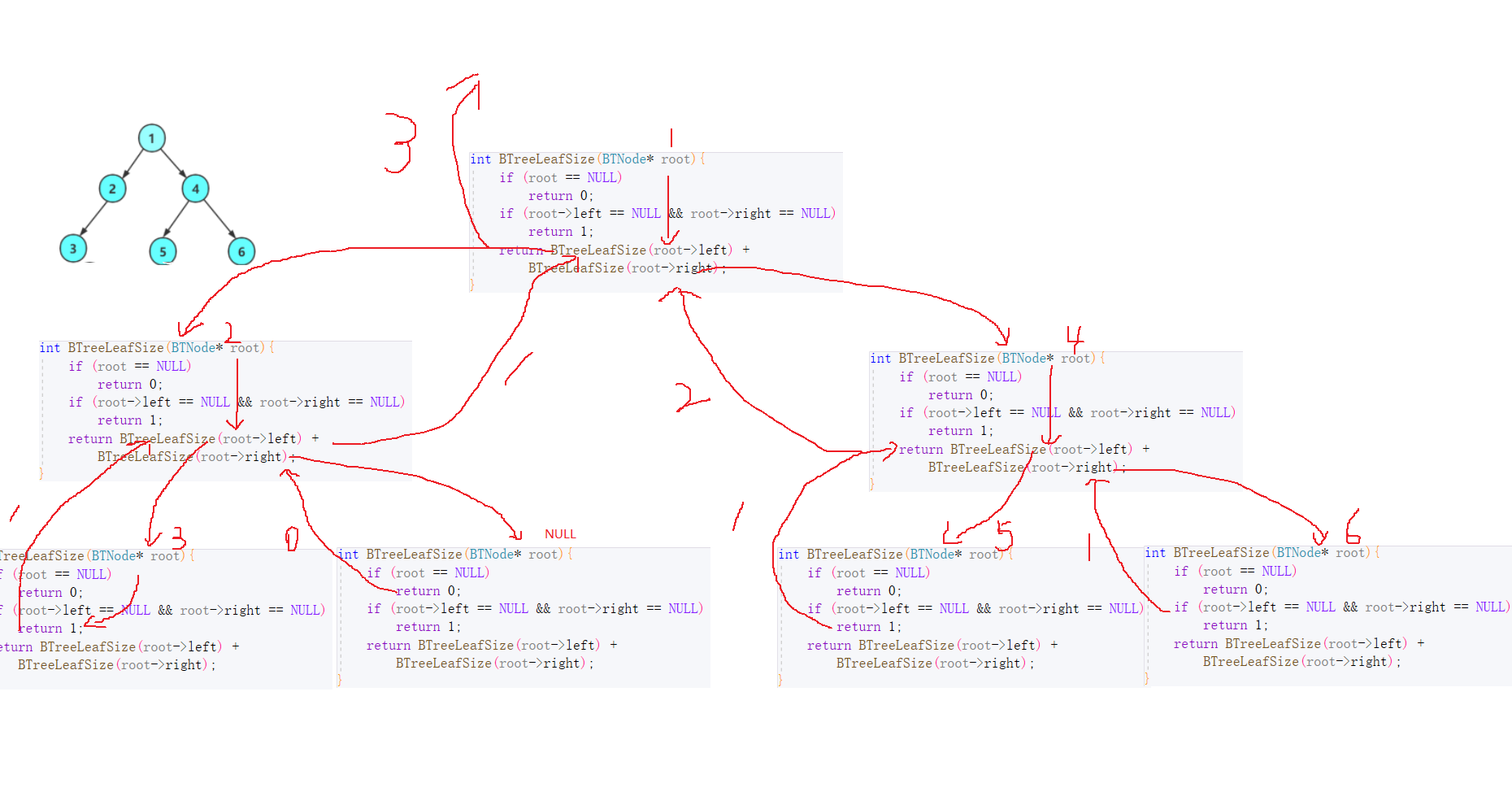
🍊3.2 叶子节点个数及递归图解

intBTreeLeafSize(BTNode* root){if(root ==NULL)return0;if(root->left ==NULL&& root->right ==NULL)return1;returnBTreeLeafSize(root->left)+BTreeLeafSize(root->right);}

🍉3.3 第k层的节点数及递归图解

intBTreeKLevelSize(BTNode* root,int k){assert(k >=1);if(root ==NULL)return0;if(k ==1)return1;returnBTreeKLevelSize(root->left, k -1)+BTreeKLevelSize(root->right, k -1);}

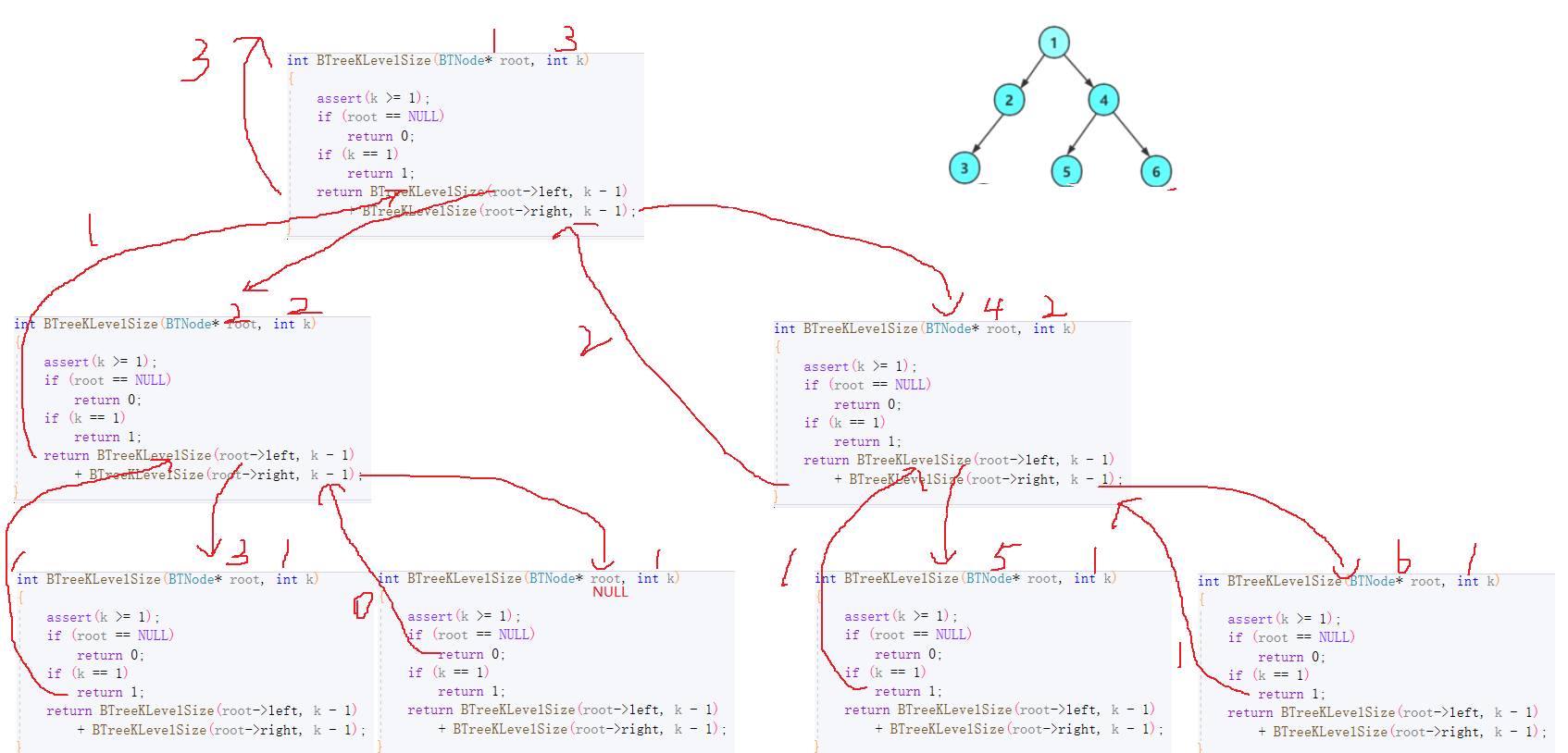
🍀3.4 二叉树的深度及递归图解

intBTreeDepth(BTNode* root){if(root ==NULL)return0;int leftDepth =BTreeDepth(root->left);int rightDepth =BTreeDepth(root->right);return leftDepth > rightDepth ? leftDepth +1: rightDepth +1;}

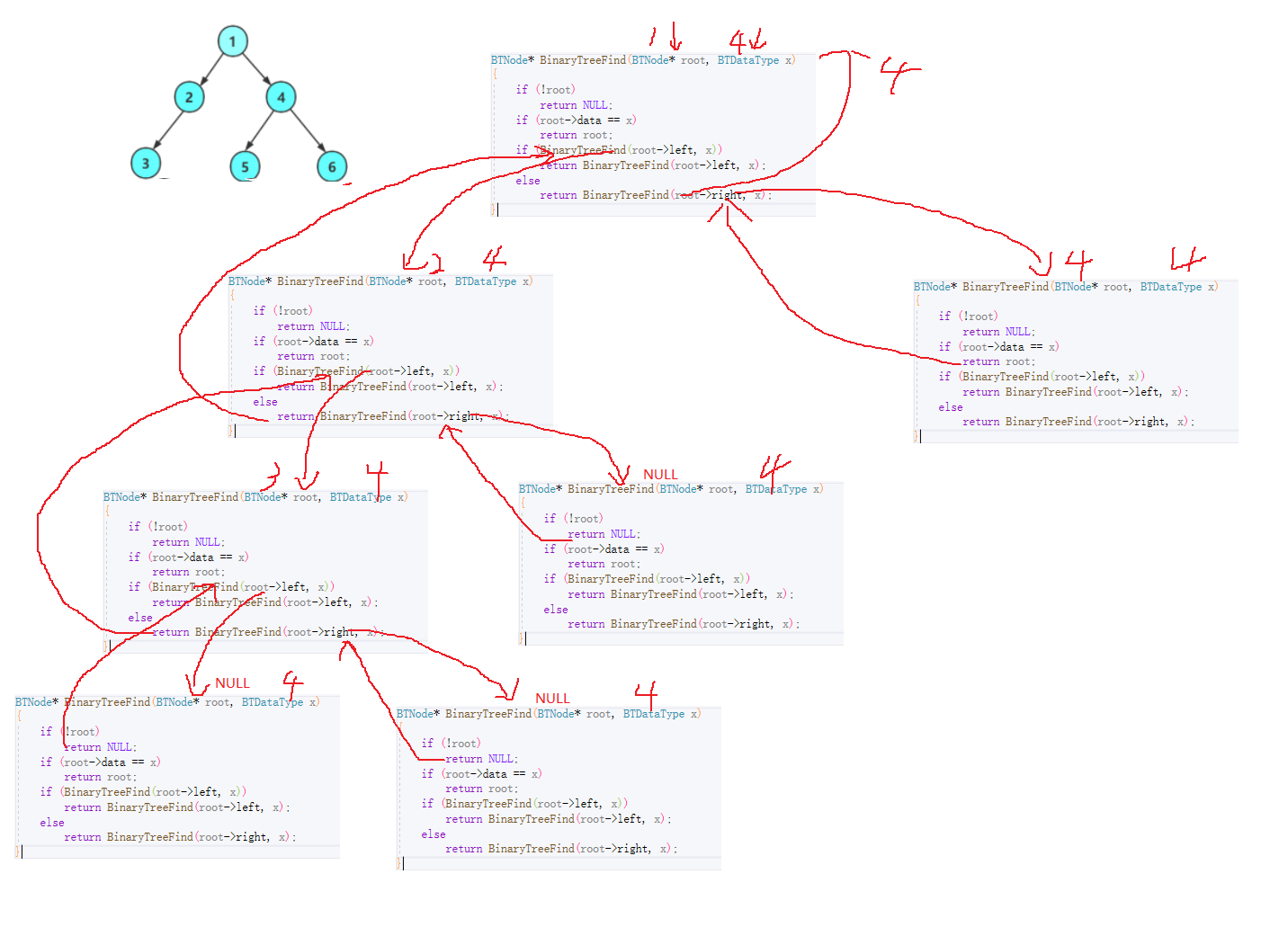
🍒3.5 二叉树查找值为x的节点及递归图解

// 二叉树查找值为x的节点
BTNode*BinaryTreeFind(BTNode* root, BTDataType x){if(!root)returnNULL;if(root->data == x)return root;if(BinaryTreeFind(root->left, x))returnBinaryTreeFind(root->left, x);elsereturnBinaryTreeFind(root->right, x);}

🍭4.总结