在分类问题中,调整用于决策的概率阈值是一个常被忽视但却简单有效的步骤。这个过程不仅容易实施,还能显著提升模型质量。对于大多数分类问题,这都是一个值得执行的步骤(根据具体的优化目标,也存在一些例外情况)。
本文将深入探讨阈值调整的具体机制 — 特别是在多类分类问题中,这个过程可能会比较复杂。我们还将介绍一个名为 ClassificationThresholdTuner 的开源工具,这是笔者开发的一个自动化阈值调整和解释的工具。
考虑到阈值调整在分类问题中的普遍性,以及不同项目间这一过程的相似性,我已经在多个项目中成功应用了这个工具。它不仅消除了大量重复代码的需求,还能提供比我们通常能够获得的更多关于阈值调整的信息。
虽然 ClassificationThresholdTuner 是一个实用工具,但本文介绍的底层原理更具参考价值 — 这些概念足够简单,可以在分类项目中轻松复现。
ClassificationThresholdTuner 是一个用于优化分类问题阈值设置并清晰展示不同阈值影响的工具。与大多数现有选项(以及自行开发的优化阈值代码)相比,它具有两个主要优势:
- 提供可视化功能,帮助数据科学家理解最优阈值的影响,以及可能的替代阈值选择。这在展示建模决策时特别有价值,例如在需要在假阳性和假阴性之间寻求平衡时。这通常需要结合业务理解和数据建模知识,而对阈值选择有清晰全面的理解可以促进讨论并帮助做出最佳决策。
- 支持多类分类,这是机器学习中常见但在阈值调整方面比二元分类更复杂的问题类型(例如需要确定多个阈值)。遗憾的是,优化多类分类的阈值在其他同类工具中支持不足。
尽管支持多类分类是 ClassificationThresholdTuner 的重要特性之一,但二元分类更容易理解,因此我们将从二元分类开始讨论。
分类中的阈值是什么?
几乎所有现代分类器(包括 scikit-learn、CatBoost、LGBM、XGBoost 等)都支持生成预测和概率。
例如我们创建一个二元分类器来预测客户在下一年是否会流失,那么对于每个客户,我们通常可以生成二元预测(是或否),或者生成一个概率值(估计一个客户在该时间范围内流失的概率为 0.862)。
给定一个能够生成概率的分类器,即使我们要求二元预测,它在后台通常也会为每条记录生成概率。然后会将这些概率转换为类别预测。
默认情况下,二元分类器会在正类的预测概率大于或等于 0.5 时预测正类,在概率小于 0.5 时预测负类。在这个流失预测的例子中,默认情况下,如果流失的预测概率 ≥ 0.5,则预测为"是",否则预测为"否"。
这可能不是最理想的行为,通常使用 0.5 以外的阈值可能会产生更好的结果,可能是略低或略高的阈值,有时甚至是与 0.5 相差较大的阈值。这取决于数据、构建的分类器以及假阳性与假阴性的相对重要性。
为了创建一个强大的模型(包括很好地平衡假阳性和假阴性),我们通常希望优化某些指标,如 F1 得分、F2 得分(或 f-beta 指标族中的其他指标)、Matthews 相关系数(MCC)、Kappa 得分等。优化这些指标的一个关键部分就是适当设置阈值,这通常会将阈值设置为 0.5 以外的值。
通常并不能立即确定最佳阈值应该设置在哪里,但我们通常可以确定要优化的最佳指标。例如在希望更多地强调正类召回率的情况下,可能会使用 F2 或 F3 分数。
Scikit-learn 对阈值调整的支持
Scikit-learn 在其调整类别预测的决策阈值页面中提供了关于阈值调整思想的详细背景。Scikit-learn 还提供了两个工具:FixedThresholdClassifier 和 TunedThresholdClassifierCV(在 scikit-learn 1.5 版本中引入)来辅助阈值调整。它们的工作方式与 ClassificationThresholdTuner 非常相似。
Scikit-learn 的这些工具可以被视为便利方法,因为它们并不是严格必需的;至少对于二元分类情况,调整是相对简单的。有这些工具确实很方便 — 调用这些工具仍然比自己编写过程要容易得多。
但是ClassificationThresholdTuner 是作为这些工具的替代方案而创建的,如果有一个二元分类问题,并且不需要对发现的阈值进行任何解释或描述,那么 scikit-learn 的工具可以完美胜任,甚至可能更方便一些,因为它们可以直接使用。
但在需要解释发现的阈值(包括与替代阈值值相关的一些上下文)或者有多类分类问题的情况下,ClassificationThresholdTuner 会更有价值。
二元分类中的阈值
对于大多数 scikit-learn 分类器以及 CatBoost、XGBoost 和 LGBM,通过调用 predict_proba() 返回每条记录的概率。该函数为每个类别输出每条记录的概率。在二元分类问题中,它们将为每条记录输出两个概率,例如:
[[0.6, 0.4],
[0.3, 0.7],
[0.1, 0.9],
…
]
对于每对概率,我们可以将第一个视为负类的概率,第二个视为正类的概率。
对于二元分类,一个概率只是 1.0 减去另一个,所以严格来说只需要其中一个类别的概率即可。实际上在处理二元分类问题的类别概率时,我们通常只使用正类的概率,因此可以使用这样的数组:[0.4, 0.7, 0.9, …]。
这样阈值很容易理解,因为它们可以简单地视为预测正类所需的最小预测概率(在流失示例中,预测客户流失)。如果我们有一个阈值,比如说 0.6,那么很容易将上面的概率数组转换为预测,在这种情况下,转换为:[否,是,是,….]。
通过使用不同的阈值,可以允许模型更加或更少地倾向于预测正类。如果使用相对较低的阈值,比如说 0.3,那么即使只有中等程度的确定性,模型也会预测正类。与使用 0.5 作为阈值相比,会做出更多正类的预测,增加真阳性和假阳性,同时也减少真阴性和假阴性。
在流失预测的情况下,如果想专注于捕捉大多数流失案例,即使这样做会导致一些非流失客户被错误地标记为流失,这种方法可能会有用。如果假阴性(漏掉流失)比假阳性(错误预测流失)更成问题,那么低阈值是合适的。
将阈值设置得更高,比如说 0.8,将产生相反的效果:预测流失的客户会更少,但在那些预测流失的客户中,很大一部分很可能真的会流失。我们则会增加假阴性(漏掉一些实际会流失的客户),但减少假阳性。这样只能跟进少数可能流失的客户,并且只想标记那些最有可能流失的客户,这可能是合适的。
在决定阈值设置位置时,几乎总是有很强的业务考量。像 ClassificationThresholdTuner 这样的工具可以使这些决策更加清晰,因为对于阈值通常没有明显的最佳点。简单地基于直觉选择阈值(例如,认为 0.7 感觉差不多)很可能不会产生最优结果,通常不会比简单使用 0.5 的默认值更好。
设置阈值可能有点反直觉:稍微调整它可能会对模型产生超出预期的帮助或伤害。例如增加阈值通常可以大大减少假阳性,对假阴性的影响却很小;在其他情况下可能恰恰相反。使用ROC曲线是帮助可视化这些权衡的好方法。我们将在后面看到一些例子。
而ClassificationThresholdTuner 本质上是一个自动化和描述该过程的工具。
AUROC 和 F1 分数
一般来说,我们可以将用于分类的指标分为三种主要类型:
- 检查预测概率排名的好坏,例如:AUROC,精确度,AUPRC
- 检查预测概率校准程度的好坏,例如:Brier 分数,对数损失
- 检查预测标签正确性的,例如:F1 分数,F2 分数,MCC,Kappa 分数,平衡准确率
这里列出的前两类指标基于预测概率工作,最后一类基于预测标签工作。
虽然每个类别中都有许多指标,但为了简化讨论,我们暂时只考虑两个较为常见的指标:AUROC和 F1 分数。
这两个指标之间存在一个有趣的关系(AUROC 与其他基于预测标签的指标也是如此),ClassificationThresholdTuner 利用这一点来调整和解释最佳阈值。
ClassificationThresholdTuner 的核心思想是,一旦模型被很好地调整以获得强大的 AUROC,就利用这一点来优化其他指标 — 基于预测标签的指标,如 F1 分数。
基于预测标签的指标
在许多情况下,检查预测标签正确性的指标是最相关的。这适用于模型将被用于为记录分配预测标签的情况,其中相关的是真阳性、真阴性、假阳性和假阴性的数量。如果下游使用的是预测标签,那么一旦分配了标签,底层预测概率的具体值就不再相关,只有这些最终的标签预测才是重要的。
如果模型为客户分配了"是"和"否"的标签,表示他们是否预计在下一年流失,并且预测为"是"的客户接受某种处理,而预测为"否"的客户不接受处理,那么最相关的是这些标签的正确性,而不是最终这些类别预测所基于的预测概率的排名或校准程度。所以正如我们将看到的,预测概率的排名对于准确分配预测标签确实是相关的。
但这并不适用于每个项目:在某些情况下,像 AUROC 或 AUPRC 这样衡量预测概率排名的指标可能是最相关的;而在其他情况下,像 Brier 分数和对数损失这样衡量预测概率准确度的指标可能最为重要。
调整阈值不会影响这些指标,因此在这些指标最为相关的情况下,没有必要调整阈值。但是对于本文,我们将考虑 F1 分数或其他基于预测标签的指标是我们希望优化的情况。
ClassificationThresholdTuner 从预测概率开始(可以用 AUROC 评估其质量),然后努力优化指定的指标(该指标是基于预测标签的)。基于预测标签正确性的指标都以不同的方式从混淆矩阵计算得出。而混淆矩阵又基于所选择的阈值,并且根据使用低阈值还是高阈值可能会有显著不同。
调整阈值
AUROC 指标,顾名思义,是基于 ROC 的,ROC 是一条显示真阳性率与假阳性率关系的曲线。ROC 曲线本身并不假设使用任何特定的阈值。但是曲线上的每个点对应一个特定的阈值。
在下面的图中,蓝色曲线是 ROC。这条曲线下的面积(AUROC)衡量了模型的总体性能,是在所有潜在阈值上的平均值。它衡量概率的排名质量:如果概率排名良好,那么被分配更高正类预测概率的记录实际上更可能属于正类。
例如,AUROC 为 0.95 意味着随机选择的正样本有 95% 的机会比随机选择的负样本获得更高的排名。
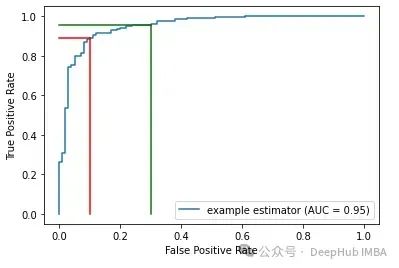
拥有一个 AUROC 强大的模型很重要 — 这是模型调优过程的目标(尽管实际上可能会优化其他指标)。这是在我们开始调整阈值之前完成的。
然后如果项目需要为所有记录进行类别预测,就有必要选择一个阈值(尽管可以使用 0.5 的默认值,但结果可能不是最佳的),这相当于在 ROC 曲线上选择一个点。
上图显示了 ROC 上的两个点。对于每个点,都绘制了一条垂直线和一条水平线到 x 轴和 y 轴,以指示相关的真阳性率和假阳性率。
给定一个 ROC 曲线,向左和向下移动时,我们使用更高的阈值(例如从绿线到红线)。预测为正的记录会更少,所以真阳性和假阳性都会减少。
向右和向上移动时(例如,从红线到绿线),使用更低的阈值。预测为正的记录会更多,所以真阳性和假阳性都会增加。
也就是说在这里的图中,红线和绿线代表两个可能的阈值。从绿线移动到红线,我们看到真阳性率略有下降,但假阳性率下降更多,这使得它很可能是比绿线所在位置更好的阈值选择。但这并不是必然的 — 我们还需要考虑假阳性和假阴性的相对成本。
从一个阈值移动到另一个阈值通常可以调整假阳性率比真阳性率更多或更少。以下展示了给定 ROC 曲线的一组阈值。我们可以看到,从一个阈值移动到另一个阈值可能对真阳性率和假阳性率产生显著不同的影响。
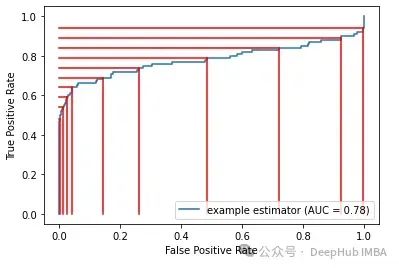
这就是调整阈值的主要思想:通常可以在一个方面获得较大收益,同时在另一个方面只承受较小损失。
可以查看 ROC 曲线并观察上下移动阈值的效果。所以可以在一定程度上通过目视检查来选择一个看起来最能平衡真阳性和假阳性的点(这也有效地平衡了假阳性和假阴性)。这就是 ClassificationThresholdTuner 所做的,但它以一种系统的方式进行,以优化某个特定的指定指标(如 F1 分数)。
将阈值移动到 ROC 上的不同点会生成不同的混淆矩阵,然后可以将其转换为指标(F1 分数、F2 分数、MCC 等)。然后我们可以选择优化这个分数的点。
只要模型训练得到强大的 AUROC,我们通常就可以找到一个好的阈值来实现高 F1 分数(或其他类似指标)。
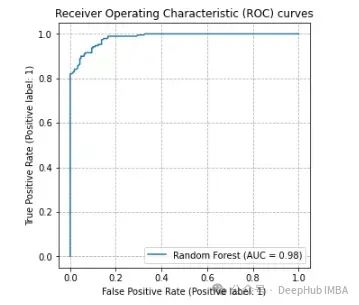
在这个 ROC 图中,模型非常准确,AUROC 为 0.98。因此,就有可能选择一个导致高 F1 分数的阈值,尽管仍然有必要选择一个好的阈值,最佳值很可能不是 0.5。
排名良好并不意味着模型也一定校准得很好:只要属于正类的记录倾向于获得比负类更高的预测概率,我们就可以找到一个好的阈值,在那里我们将预测为正的与预测为负的分开。
从另一个角度来看,可以用两个直方图来查看二元分类问题中概率的分布,如这里所示(实际上使用核密度估计KDE图)。蓝色曲线显示负类的概率分布,橙色显示正类的概率分布。模型可能没有很好地校准:正类的概率始终远低于 1.0。但它们排名良好:正类的概率往往高于负类的概率,这意味着模型会有很高的 AUROC,如果使用适当的阈值,模型可以很好地分配标签,在这种情况下,可能约为 0.25 或 0.3。鉴于分布有重叠,不可能有一个完美的系统来标记记录,F1 分数永远不可能完全达到 1.0。
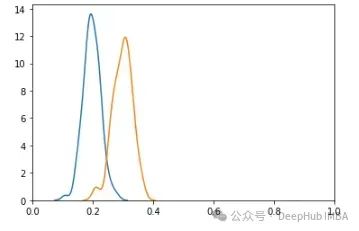
即使 AUROC 分数很高,也可能出现 F1 分数低的情况:当选择了不合适的阈值时。例如,当 ROC 贴近轴时,如上面所示的 ROC — 非常低或非常高的阈值可能效果不佳。当数据不平衡时,也可能出现贴近 y 轴的情况。
在这里显示的直方图中,尽管模型校准良好并且会有高 AUROC 分数,但不恰当的阈值选择(如 0.5 或 0.6,这会导致所有内容都被预测为负类)会导致非常低的 F1 分数。也可能出现 AUROC 低而 F1 分数高的情况。这在特别好的阈值选择下是可能的(尽管大多数阈值都会表现不佳)。
虽然不常见,但 ROC 曲线可能是不对称的,这可能极大地影响最佳放置阈值的位置。
使用 ClassificationThresholdTuner 进行二元分类的示例
这是取自github上提供的代码。我们将在这里讨论主要点。对于这个例子,首先生成一个测试数据集。
importpandasaspd
importnumpyasnp
importmatplotlib.pyplotasplt
importseabornassns
fromthreshold_tunerimportClassificationThresholdTuner
NUM_ROWS=100_000
defgenerate_data():
num_rows_per_class=NUM_ROWS//2
np.random.seed(0)
d=pd.DataFrame(
{"Y": ['A']*num_rows_per_class+ ['B']*num_rows_per_class,
"Pred_Proba":
np.random.normal(0.7, 0.3, num_rows_per_class).tolist() + \
np.random.normal(1.4, 0.3, num_rows_per_class).tolist()
})
returnd, ['A', 'B']
d, target_classes=generate_data()
为了简化示例,我们不生成原始数据或产生预测概率的分类器,而只生成一个包含真实标签和预测概率的测试数据集,因为这就是 ClassificationThresholdTuner 使用的内容,也是选择最佳阈值所需的全部信息。
实际上还有代码来缩放概率,以确保它们在 0.0 和 1.0 之间,但在这里,我们只是假设概率已经很好地缩放了。然后我们可以使用 0.5 的阈值设置 Pred 列:
d['Pred'] =np.where(d["Pred_Proba"] >0.50, "B", "A")
这模拟了通常对分类器所做的操作,简单地使用 0.5 作为阈值。这是我们将尝试改进的基线。
然后我们创建一个 ClassificationThresholdTuner 对象,并使用它,首先只是评估当前预测的性能,调用其中一个 API, print_stats_lables()。
tuner=ClassificationThresholdTuner()
tuner.print_stats_labels(
y_true=d["Y"],
target_classes=target_classes,
y_pred=d["Pred"])
这显示了两个类的精确度、召回率和 F1 分数(以及这些的宏观分数),并呈现混淆矩阵。
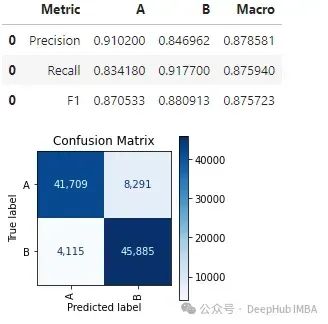
这个 API 假设标签已经被预测;如果只有概率可用,则不能使用此方法,尽管我们总是可以像在这个例子中那样,选择一个阈值并基于此设置标签。
还可以调用 print_stats_proba() 方法,它也呈现一些指标,在这种情况下与预测概率相关。它显示:Brier 分数、AUROC 和几个图表。图表需要一个阈值,如果没有指定,则使用 0.5:
tuner.print_stats_proba(
y_true=d["Y"],
target_classes=target_classes,
y_pred_proba=d["Pred_Proba"])
这显示了使用 0.5 阈值的效果。它显示 ROC 曲线,曲线本身不需要阈值,但在曲线上绘制了阈值。然后它呈现了基于阈值如何将数据分为两个预测类,首先是直方图,其次是群体图。这里有两个类,类 A 用绿色表示,类 B(在这个例子中是正类)用蓝色表示。
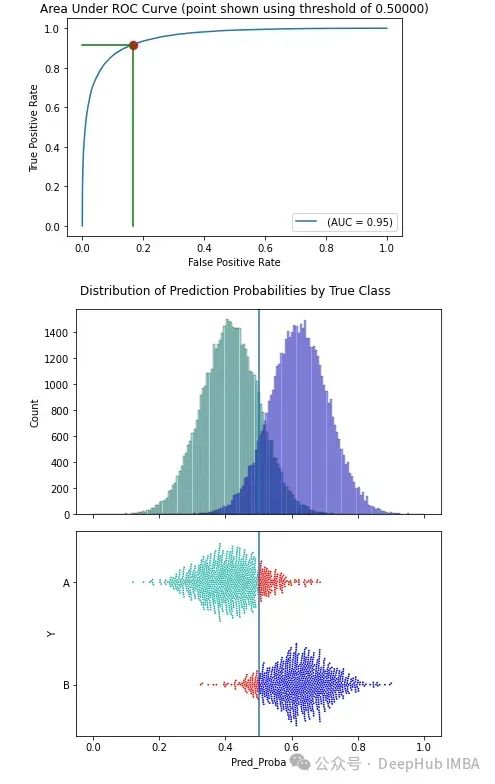
在群体图中,任何错误分类的记录都显示为红色。这些是真实类为 A 但 B 的预测概率高于阈值的记录(因此模型会预测 B),以及真实类为 B 但 B 的预测概率低于阈值的记录(因此模型会预测 A)。
然后可以使用 plot_by_threshold() 检查不同阈值的效果:
tuner.plot_by_threshold(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d["Pred_Proba"])
在这个例子中,使用默认的一组潜在阈值:0.1、0.2、0.3、...直到 0.9。对于每个阈值,它将预测任何预测概率高于阈值的记录为正类,低于阈值的为负类。错误分类的记录显示为红色。
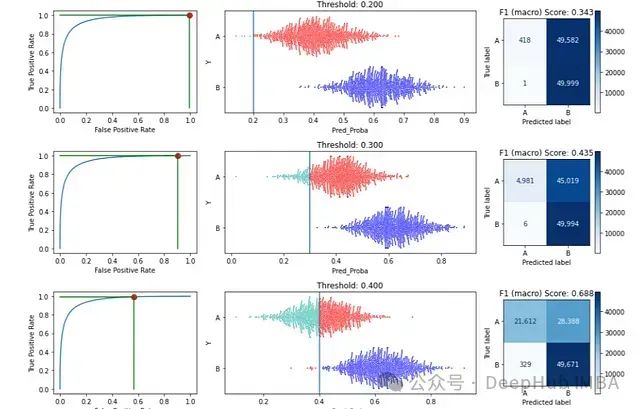
这张图只显示了三个潜在的阈值:0.2、0.3 和 0.4。对于每个阈值可以看到:阈值在 ROC 曲线上代表的位置,它导致的数据分割,以及由此产生的混淆矩阵(以及与该混淆矩阵相关的 F1 宏观分数)。
将阈值设置为 0.2 会导致几乎所有内容都被预测为 B(正类) — 几乎所有 A 类的记录都被错误分类,因此被绘制成红色。随着阈值的增加,更多的记录被预测为 A,更少的被预测为 B(尽管在 0.4 时,大多数真实为 B 类的记录被正确预测为 B;直到阈值约为 0.8 时,几乎所有真实为 B 类的记录才被错误地预测为 A:很少有预测概率超过 0.8 的)。
检查从 0.1 到 0.9 的九个可能值可以很好地概述可能的阈值,但调用这个函数来显示更窄、更现实的可能值范围可能更有用,例如:
tuner.plot_by_threshold(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d["Pred_Proba"],
start=0.50, end=0.55, num_steps=6)
这将显示从 0.50 到 0.55 的每个阈值。显示其中的前两个:
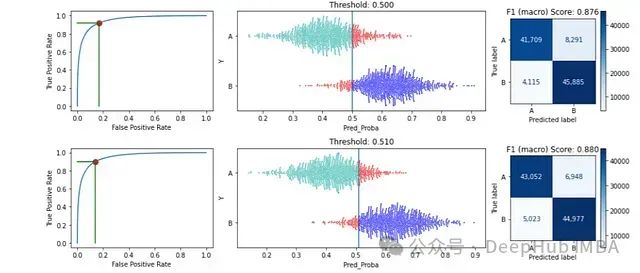
还可以通过调用 describe_slices() 来查看潜在阈值对之间的数据(即在数据的切片内),以便更清楚地看到将阈值从一个潜在位置移动到下一个位置会带来的具体变化(我们看到每个真实类有多少会被重新分类)。
tuner.describe_slices(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d["Pred_Proba"],
start=0.3, end=0.7, num_slices=5)
这以可视化和表格格式显示每个切片:
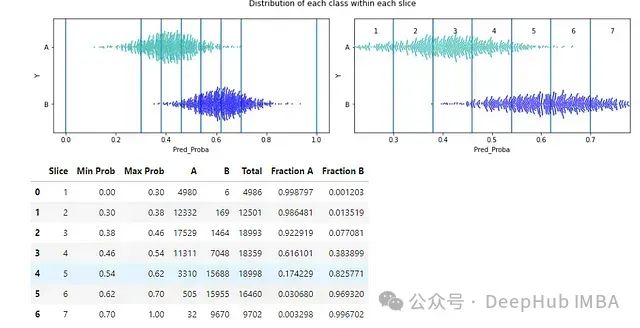
在这里,切片相当薄,所以看到的图表既显示它们在完整概率范围的上下文中(左图),也显示了放大后的视图(右图)。
我们可以看到,将阈值从 0.38 移动到 0.46,会重新分类第 3 个切片中的点,其中有 17,529 个 A 类的真实实例和 1,464 个 B 类的真实实例。这在最右边的群体图和表格中都很明显(在群体图中,切片 3 内的绿点远多于蓝点)。
这个 API 也可以针对更窄、更现实的潜在阈值范围进行调用:
tuner.describe_slices(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d["Pred_Proba"],
start=0.4, end=0.6, num_slices=10)
这产生:
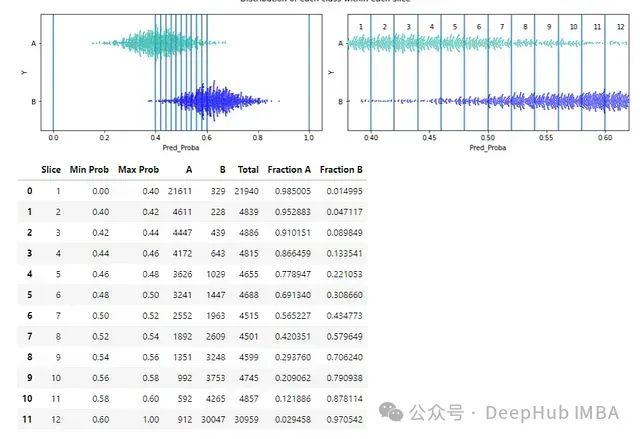
在调用这些(或另一个有用的 API, print_stats_table(),为简洁起见在这里跳过,但在 github 页面中有描述)
然后我们可以转向主要任务,使用 tune_threshold() API 搜索最佳阈值。对于某些项目,这实际上可能是唯一调用的 API。或者它可能首先被调用,之后调用上述 API 来为发现的最佳阈值提供上下文。
在这个例子中,我们的目标是优化 F1 宏观分数,尽管任何由 scikit-learn 支持并基于类别标签的指标都是可能的。一些指标需要额外的参数,这些参数也可以在这里传递。在这个例子中,scikit-learn 的 f1_score() 需要 'average' 参数,作为参数传递给 tune_threshold()。
fromsklearn.metricsimportf1_score
best_threshold=tuner.tune_threshold(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d["Pred_Proba"],
metric=f1_score,
average='macro',
higher_is_better=True,
max_iterations=5
)
best_threshold
这可选地显示一组图表,演示该方法如何在五次迭代中(在这个例子中 max_iterations 被指定为 5)缩小到优化指定指标的阈值。
第一次迭代考虑 0.0 到 1.0 之间的全范围潜在阈值。然后它缩小到 0.5 到 0.6 的范围,这在下一次迭代中被更仔细地检查,依此类推。最终选择了 0.51991 的阈值。
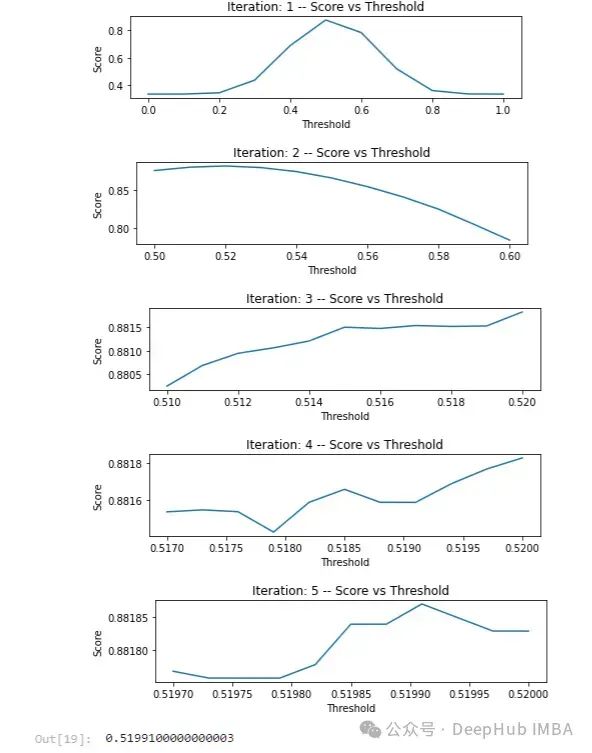
在此之后,我们可以再次调用 print_stats_labels(),它显示:
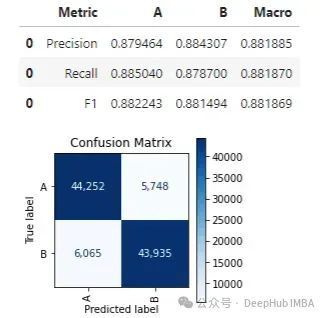
在这个例子中,宏观 F1 分数从 0.875 增加到 0.881。收益相对较小,但几乎是免费获得的。在其他情况下,收益可能更小或更大,有时可能会显著提高。它也不会产生负面影响;最坏的情况下,发现的最佳阈值将是默认的 0.5000,不会导致性能下降。
多类分类中的阈值
如前所述,多类分类稍微复杂一些。在二元分类情况下,选择单个阈值,但对于多类分类,ClassificationThresholdTuner 为每个类别识别一个最佳阈值。
与二元情况不同的是,需要指定一个类别作为默认类别。通过一个例子应该可以更清楚地说明为什么会这样。
在许多情况下,有一个默认类别可能相当自然。例如,如果目标列代表各种可能的医疗状况,默认类别可能是"无问题",其他类别可能每个都与特定状况相关。对于这些条件中的每一个,都会有一个最小预测概率,我们需要这个概率才能实际预测该条件。
或者说如果数据代表网络日志,目标列与各种入侵类型相关,那么默认可能是"正常行为",其他类别每个都与特定网络攻击相关。
在网络攻击的例子中,可能有一个具有四个不同目标值的数据集,目标列包含类别:"正常行为"、"缓冲区溢出"、"端口扫描"和"钓鱼"。对于运行预测的任何记录,将得到每个类别的概率,这些概率的总和为 1.0。我们可能得到,例如:0.3, 0.4, 0.1, 0.2。
通常,我们会预测"缓冲区溢出",因为它有最高的概率 0.4。但是我们可以设置一个阈值来修改这种行为,这将影响这个类别的假阴性和假阳性率。
例如:"正常行为"是默认类别;"缓冲区溢出"的阈值为 0.5;"端口扫描"为 0.55;"钓鱼"为 0.45。按照惯例,默认类别的阈值设置为 0.0,因为它实际上不使用阈值。所以这里的阈值集合将是:0.0, 0.5, 0.55, 0.45。
然后对于任何给定记录进行预测时,我们只考虑概率超过相关阈值的类别。在这个例子中(预测为[0.3, 0.4, 0.1, 0.2]),没有一个概率超过其阈值,所以预测默认类别"正常行为"。
如果预测概率是:[0.1, 0.6, 0.2, 0.1],那么我们会预测"缓冲区溢出":概率(0.6)是最高的预测,并且超过其阈值(0.5)。
如果预测概率是:[0.1, 0.2, 0.7, 0.0],那么我们会预测"端口扫描":概率(0.7)超过其阈值(0.55),这是最高的预测。
如果一个或多个类别的预测概率超过其阈值,我们取其中预测概率最高的一个。如果没有超过它们的阈值,我们取默认类别。如果默认类别有最高的预测概率,它将被预测。
所以需要一个默认类别来覆盖没有预测超过该类别阈值的情况。
如果预测是:[0.1, 0.3, 0.4, 0.2],阈值是:0.0, 0.55, 0.5, 0.45,另一种看待这个的方式是:通常会预测第三个类别:它有最高的预测概率(0.4)。但是如果该类别的阈值是 0.5,那么 0.4 的预测不够高,所以我们转到下一个最高的预测,即第二个类别,预测概率为 0.3。这低于其阈值,所以我们再次转到下一个最高的预测概率,即第四个类别,预测概率为 0.2。它也低于该目标类别的阈值。在这里虽然我们有所有类别的预测都相当高,但不够高(没达到我们设置的最低标准),所以使用默认类别。
这也突出了为什么使用 0.0 作为默认类别的阈值很方便 — 在检查默认类别的预测时,我们不需要考虑其预测是否低于或高于该类别的阈值;我们总是可以做出默认类别的预测。
原则上也可以有更复杂的策略 — 不仅仅使用单一默认类别,而是在不同条件下可以选择多个类别。但这些超出了本文的范围,并且通常是不必要的,主要是至少目前还不被 ClassificationThresholdTuner 支持。所以在本文的剩余部分,我们将假设指定了一个单一的默认类别。
使用 ClassificationThresholdTuner 进行多类分类的示例
我们将从创建测试数据开始,有三个而不是仅两个目标类别:
importpandasaspd
importnumpyasnp
importmatplotlib.pyplotasplt
importseabornassns
fromthreshold_tunerimportClassificationThresholdTuner
NUM_ROWS=10_000
defgenerate_data():
num_rows_for_default=int(NUM_ROWS*0.9)
num_rows_per_class= (NUM_ROWS-num_rows_for_default) //2
np.random.seed(0)
d=pd.DataFrame({
"Y": ['No Attack']*num_rows_for_default+ ['Attack A']*num_rows_per_class+ ['Attack B']*num_rows_per_class,
"Pred_Proba No Attack":
np.random.normal(0.7, 0.3, num_rows_for_default).tolist() + \
np.random.normal(0.5, 0.3, num_rows_per_class*2).tolist(),
"Pred_Proba Attack A":
np.random.normal(0.1, 0.3, num_rows_for_default).tolist() + \
np.random.normal(0.9, 0.3, num_rows_per_class).tolist() + \
np.random.normal(0.1, 0.3, num_rows_per_class).tolist(),
"Pred_Proba Attack B":
np.random.normal(0.1, 0.3, num_rows_for_default).tolist() + \
np.random.normal(0.1, 0.3, num_rows_per_class).tolist() + \
np.random.normal(0.9, 0.3, num_rows_per_class).tolist()
})
d['Y'] =d['Y'].astype(str)
returnd, ['No Attack', 'Attack A', 'Attack B']
d, target_classes=generate_data()
实际上还有代码来缩放分数并确保它们的总和为 1.0,但在这里我们可以假设这已经完成,有一组为每个记录的每个类别形成良好的概率。
与真实世界的数据一样,其中一个类别('No Attack'类)比其他类别更频繁;数据集是不平衡的。
然后我们设置目标预测,暂时只取概率最高的类别:
defset_class_prediction(d):
max_cols=d[proba_cols].idxmax(axis=1)
max_cols= [x[len("Pred_Proba_"):] forxinmax_cols]
returnmax_cols
d['Pred'] =set_class_prediction(d)
这产生:
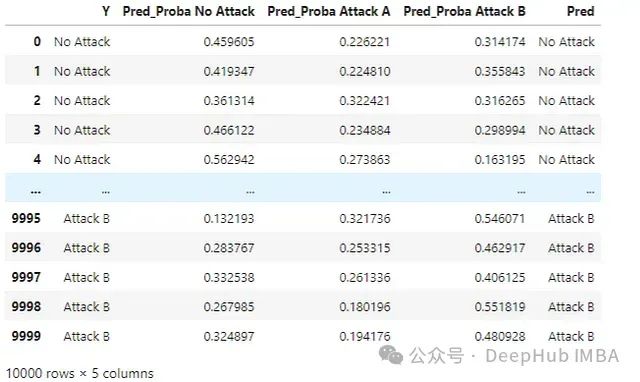
取概率最高的类别是默认行为,在这个例子中,这是我们希望改进的基线。可以像二元情况一样调用 print_stats_labels(),它的工作方式类似,可以处理任意数量的类别:
tuner.print_stats_labels(
y_true=d["Y"],
target_classes=target_classes,
y_pred=d["Pred"])
这输出:
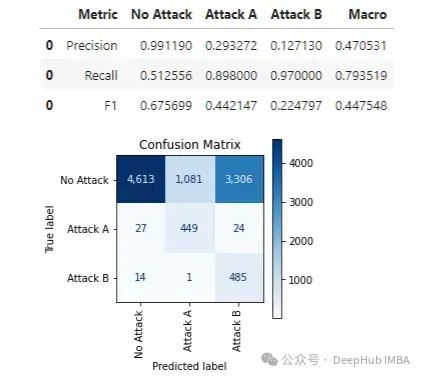
使用这些标签,我们只获得 0.447 的 F1 宏观分数。
调用 print_stats_proba(),还获得与预测概率相关的输出:
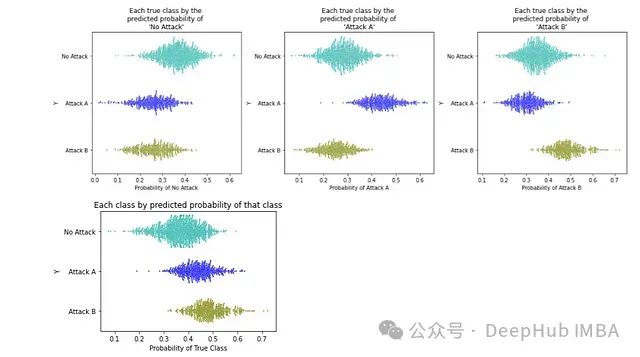
这比二元情况稍微复杂一些,因为有三个概率需要考虑:每个类别的概率。所以首先展示数据相对于每个类别概率的情况,有三个目标类别,所以第一行有三个图。
如所希望的那样,当根据"No Attack"的预测概率绘制数据时(最左边的图),该类别的记录被赋予比其他类别更高的概率。"Attack A"(中间图)和"Attack B"(最右边的图)也是如此。
还可以看到类别并没有完美分离,也就是说没有一组阈值可以产生完美的混淆矩阵。我们需要选择一组阈值,以最好地平衡每个类别的正确和错误预测。
在上图中,底部的图显示了每个点基于其真实类别的概率。对于真实类别是"No Attack"的记录(绿色点),根据它们预测为"No Attack"的概率绘制这些点,对于真实类别是"Attack A"的记录(深蓝色),根据它们预测为"Attack A"的概率绘制这些点,对"Attack B"也是类似的(深黄色)。看到模型对"Attack A"和"Attack B"的概率相似,并且这些概率比"No Attack"的概率高。
上面的图没有考虑可能使用的任何具体阈值。所以还可以选择生成更多输出,传递一组阈值(每个类别一个,默认类别使用 0.0):
tuner.print_stats_proba(
y_true=d["Y"],
target_classes=target_classes,
y_pred_proba=d[proba_cols].values,
default_class='No Attack',
thresholds=[0.0, 0.4, 0.4]
)
这可能最有用于绘制工具发现的最佳阈值集,但也可以用于查看其他潜在的阈值集。
这为每个类别生成一个报告。为了节省空间,我们这里只显示一个,即 Attack A 类别的报告(完整报告在示例中显示;查看其他两个类别的报告也有助于理解在这个例子中使用[0.0, 0.4, 0.4]作为阈值的全部影响):

由于我们在这里指定了一组阈值,可以看到使用这些阈值的影响,包括每个类别将有多少被正确和错误分类。
首先看到阈值在 ROC 曲线上的位置。在这种情况下,看到 0.4 的阈值(在上面的 API 调用中为 class A 指定了 0.4)。
还显示了 AUROC 分数。这个指标只适用于二元预测,但在多类问题中,可以通过将问题视为一系列一对全问题来计算每个类别的 AUROC 分数。这里我们可以将问题视为"Attack A"对非"Attack A"(其他报告也类似)。
接下来的图显示了每个类别相对于 Attack A 的预测概率的分布。由于不同类别的计数不同,这些以两种方式显示:一种显示实际分布,另一种显示经过缩放以更具可比性的分布。前者更相关,但后者可以让所有类别在某些类别比其他类别罕见得多的情况下清晰可见。
真实类别为"Attack A"的记录(深蓝色)确实有更高的"Attack A"预测概率,但在具体放置阈值的位置上需要做出一些决定。所以我们在这里使用 0.4 作为这个类别的效果。看起来 0.4 可能接近理想,即使不是完全理想。
还以群体图的形式看到这一点(最右边的图),错误分类的点用红色表示。使用更高的阈值(比如 0.45 或 0.5),会有更多真实类别为 Attack A 的记录被错误分类,但更少真实类别为"No Attack"的记录被错误分类。而使用更低的阈值(比如 0.3 或 0.35)会产生相反的效果。
调用 plot_by_threshold() 来查看不同的潜在阈值:
tuner.plot_by_threshold(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d[proba_cols].values,
default_class='No Attack'
)
这个 API 仅用于解释而不是调优,所以为了简单起见,对每个潜在阈值使用相同的阈值(除了默认类别)。显示潜在阈值 0.2、0.3 和 0.4 的结果:
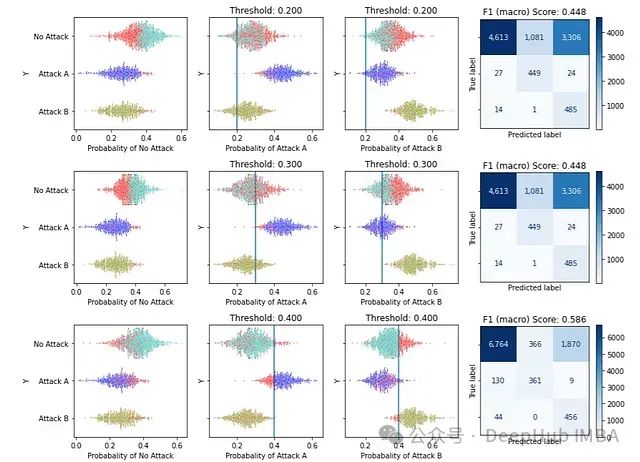
第一行图显示了对所有非默认类别使用 0.2 作为阈值的影响(即除非 Attack A 的估计概率至少为 0.2,否则不预测 Attack A;除非 Attack B 的预测概率至少为 0.2,否则不预测 Attack B — 尽管总是取概率最高的类别)。类似地,第二和第三行分别显示了阈值 0.3 和 0.4 的情况。可以在这里看到使用每个类别的较低或较高阈值的权衡,以及由此产生的混淆矩阵(以及与这些混淆矩阵相关的 F1 分数)。
在这个例子中,从 0.2 移动到 0.3 再到 0.4,模型会越来越少地预测 Attack A 或 Attack B(提高阈值,会越来越少地预测默认以外的任何东西),而越来越多地预测 No Attack,这导致真实类别为 No Attack 的错误分类减少,但真实类别为 Attack A 或 Attack B 的错误分类增加。
当阈值相当低,如 0.2 时,那些真实类别为默认类的记录中,只有预测概率最高的(大约前一半)被正确预测。
一旦阈值设置在 0.6 左右以上,几乎所有东西都被预测为默认类,所以所有真实为默认类的情况都是正确的,所有其他情况都是错误的。
设置更高的阈值意味着更频繁地预测默认类,更少地错过这些,尽管会错过更多其他类别。Attack A 和 B 在使用低阈值时通常被正确预测,但在使用更高阈值时大多被错误预测。
要调整阈值,可以使用 tune_threshold(),代码如下:
fromsklearn.metricsimportf1_score
best_thresholds=tuner.tune_threshold(
y_true=d['Y'],
target_classes=target_classes,
y_pred_proba=d[proba_cols].values,
metric=f1_score,
average='macro',
higher_is_better=True,
default_class='No Attack',
max_iterations=5
)
best_thresholds
这输出:[0.0, 0.41257, 0.47142]。也就是说,它发现对 Attack A 使用约 0.413 的阈值,对 Attack B 使用 0.471 的阈值最能优化指定的指标,在这种情况下是宏观 F1 分数。
再次调用 print_stats_proba(),我们得到:
tuner.print_stats_proba(
y_true=d["Y"],
target_classes=target_classes,
y_pred_proba=d[proba_cols].values,
default_class='No Attack',
thresholds=best_thresholds
)
这输出:

使用这里发现的阈值,宏观 F1 分数从约 0.44 提高到 0.68(结果会因运行而略有不同)。
get_predictions()
还提供了一个额外的 API,get_predictions(),它可能非常方便,用于在给定一组预测和阈值的情况下获取标签预测。可以这样调用:
tuned_pred=tuner.get_predictions(
target_classes=target_classes,
d["Pred_Proba"],
None,
best_threshold)
真实数据集的测试
也对许多真实数据集进行了测试。github 页面上包含了一个涵盖少量(四个)真实数据集的笔记本。这更多是为了提供使用该工具的真实示例和它生成的图表(而不是用于解释该工具的合成数据),但也给出了一些工具确实改善 F1 宏观分数的例子。
为了快速总结这些,就发现的阈值和 F1 宏观分数的提高而言:
乳腺癌:发现最佳阈值为 0.5465,将宏观 F1 分数从 0.928 提高到 0.953。
钢板故障:发现最佳阈值为 0.451,将宏观 F1 分数从 0.788 提高到 0.956。
表型发现最佳阈值为 0.444,将宏观 F1 分数从 0.75 提高到 0.78。
对于数字数据集,没有发现比默认值更好的改进,尽管可能使用不同的分类器或其他不同的条件可能会有改进。
在多类问题中设置阈值的影响
在多类设置中设置阈值有一些微妙的点,这可能与任何给定项目相关,也可能不相关。这可能比你的工作所需要的更深入,而且这篇文章已经相当长了,但在主 github 页面上提供了一个部分来涵盖相关的情况。特别是设置高于 0.5 的阈值可能与低于 0.5 的阈值行为略有不同。
总结
虽然调整用于分类项目的阈值并不总是能提高模型的质量,但它通常会而且通常是显著的。这很容易实现,但使用 ClassificationThresholdTuner 使这变得更加简便,对于多类分类,它可能特别有用。
它还提供了解释阈值选择的可视化,这可能有助于理解和接受它发现的阈值,或者选择其他阈值以更好地匹配项目的目标。
对于多类分类,理解移动阈值的效果可能仍然需要一些努力,但使用这样的工具比不使用要容易得多,在许多情况下,简单地调整阈值并测试结果在任何情况下都足够了。
github地址
https://github.com/Brett-Kennedy/ClassificationThresholdTuner
作者:Brett Kennedy