目录

简介
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!唯有努力💪
本文仅记录自己感兴趣的内容
torch.matmul()
语法
torch.matmul(input, other, *, out=None) → Tensor
作用
两个张量的矩阵乘积
行为取决于张量的维度,如下所示:
- 如果两个张量都是一维的,则返回点积(标量)。
- 如果两个参数都是二维的,则返回矩阵-矩阵乘积。
- 如果第一个参数是一维的,第二个参数是二维的,为了矩阵乘法的目的,在它的维数前面加上一个 1。在矩阵相乘之后,前置维度被移除。
- 如果第一个参数是二维的,第二个参数是一维的,则返回矩阵向量积。
- 如果两个参数至少为一维且至少一个参数为 N 维(其中 N > 2),则返回批处理矩阵乘法 - 如果第一个参数是一维的,则将 1 添加到其维度,以便批量矩阵相乘并在之后删除。如果第二个参数是一维的,则将 1 附加到其维度以用于批量矩阵倍数并在之后删除- 非矩阵(即批次)维度是广播的(因此必须是可广播的)- 例如,如果输入是 ( j × 1 × n × n ) (j \times 1 \times n \times n) (j×1×n×n) 张量- 另一个是 ( k × n × n ) (k \times n \times n) (k×n×n)张量,- out 将是一个 ( j × k × n × n ) (j \times k \times n \times n) (j×k×n×n) 张量
请注意,广播逻辑在确定输入是否可广播时仅查看批处理维度,而不是矩阵维度
例如
- 如果输入是 ( j × 1 × n × m ) (j \times 1 \times n \times m) (j×1×n×m) 张量
- 另一个是 ( k × m × p ) (k \times m \times p) (k×m×p) 张量
- 即使最后两个维度(即矩阵维度)不同,这些输入对于广播也是有效的
- out 将是一个 ( j × k × n × p ) (j \times k \times n \times p) (j×k×n×p) 张量
该运算符支持 TensorFloat32。
在某些 ROCm 设备上,当使用 float16 输入时,此模块将使用不同的向后精度

举例
情形1: 一维 * 一维
如果两个张量都是一维的,则返回点积(标量)
tensor1 = torch.Tensor([1,2,3])
tensor2 =torch.Tensor([4,5,6])
ans = torch.matmul(tensor1, tensor2)print('tensor1 : ', tensor1)print('tensor2 : ', tensor2)print('ans :', ans)print('ans.size :', ans.size())
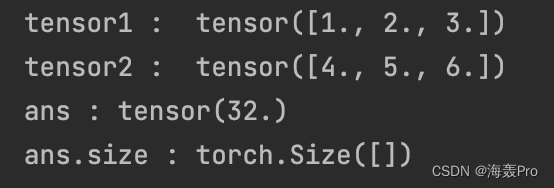
ans = 1 * 4 + 2 * 5 + 3 * 6 = 32
情形2: 二维 * 二维
如果两个参数都是二维的,则返回矩阵-矩阵乘积
也就是 正常的矩阵乘法 (m * n) * (n * k) = (m * k)
tensor1 = torch.Tensor([[1,2,3],[1,2,3]])
tensor2 =torch.Tensor([[4,5],[4,5],[4,5]])
ans = torch.matmul(tensor1, tensor2)print('tensor1 : ', tensor1)print('tensor2 : ', tensor2)print('ans :', ans)print('ans.size :', ans.size())
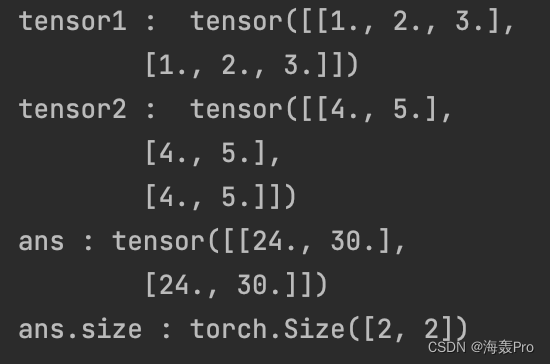
情形3: 一维 * 二维
如果第一个参数是一维的,第二个参数是二维的,为了矩阵乘法的目的,在它的维数前面加上一个 1
在矩阵相乘之后,前置维度被移除
tensor1 = torch.Tensor([1,2,3]) # 注意这里是一维
tensor2 =torch.Tensor([[4,5],[4,5],[4,5]])
ans = torch.matmul(tensor1, tensor2)print('tensor1 : ', tensor1)print('tensor2 : ', tensor2)print('ans :', ans)print('ans.size :', ans.size())
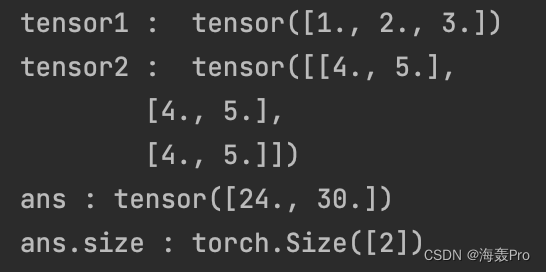
tensor1 = torch.Tensor([1,2,3])
修改为
tensor1 = torch.Tensor([[1,2,3]])
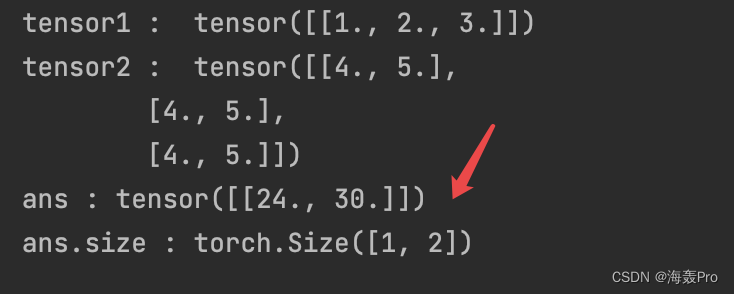
发现一个结果是
[24., 30.]
一个是
[[24., 30.]]
所以,当一维 * 二维时, 开始变成 1 * m(一维的维度),也就是一个二维, 再进行正常的矩阵运算,得到
[[24., 30.]]
, 然后再去掉开始增加的一个维度,得到
[24., 30.]
想象为二维 * 二维(前置维度为1),最后结果去掉一个维度即可
情形4: 二维 * 一维
如果第一个参数是二维的,第二个参数是一维的,则返回矩阵向量积
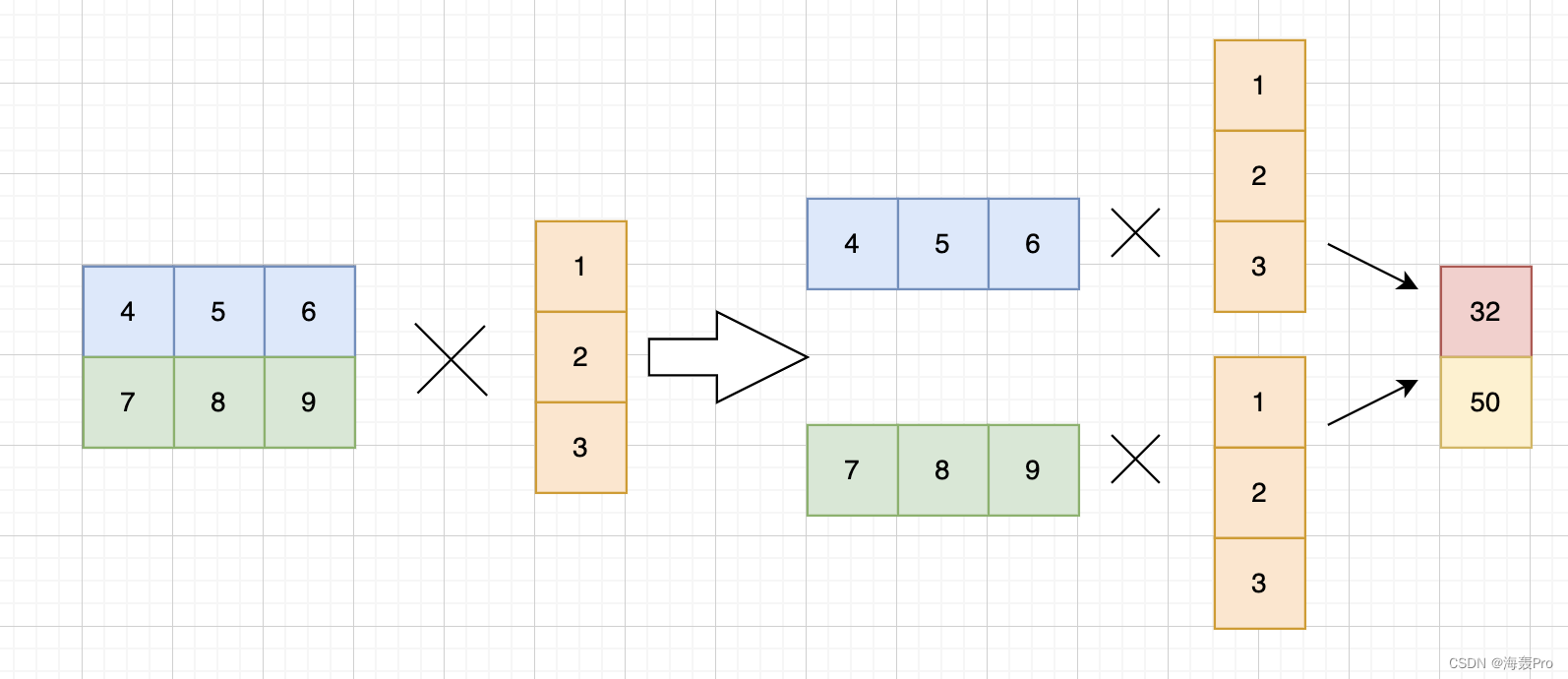
tensor1 =torch.Tensor([[4,5,6],[7,8,9]])
tensor2 = torch.Tensor([1,2,3])
ans = torch.matmul(tensor1, tensor2)print('tensor1 : ', tensor1)print('tensor2 : ', tensor2)print('ans :', ans)print('ans.size :', ans.size())
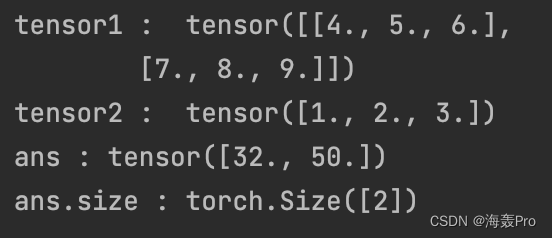
理解为:
- 把第一个二维中,想象为多个行向量
- 第二个一维想象为一个列向量
- 行向量与列向量进行矩阵乘法,得到一个标量
- 再按照行堆叠起来即可
情形5:两个参数至少为一维且至少一个参数为 N 维(其中 N > 2),则返回批处理矩阵乘法
第一个参数为N维,第二个参数为一维时
tensor1 = torch.randn(10,3,4)
tensor2 = torch.randn(4)print(torch.matmul(tensor1, tensor2).size())

(4) 先添加一个维度 (4 * 1)
得到(10 * 3 * 4) *( 4 * 1) = (10 * 3 * 1)
再删除最后一个维度(添加的那个)
得到结果(10 * 3)
tensor1 = torch.randn(10,2,3,4) #
tensor2 = torch.randn(4)print(torch.matmul(tensor1, tensor2).size())

(10 * 2 * 3 * 4) * (4 * 1) = (10 * 2 * 3) 【抵消4,删1】
第一个参数为一维,第二个参数为二维时
tensor1 = torch.randn(4)
tensor2 = torch.randn(10,4,3)print(torch.matmul(tensor1, tensor2).size())

tensor2 中第一个10理解为批次, 10个(4 * 3)
(1 * 4)与每个(4 * 3) 相乘得到(1,3),去除1,得到(3)
批次为10,得到(10,3)
tensor1 = torch.randn(4)
tensor2 = torch.randn(10,2,4,3)print(torch.matmul(tensor1, tensor2).size())

这里批次理解为[10, 2]即可
tensor1 = torch.randn(4)
tensor2 = torch.randn(10,4,2,4,1)print(torch.matmul(tensor1, tensor2).size())

个人理解:当一个参数为一维时,它要去匹配另一个参数的最后两个维度(二维 * 二维)
比如上面的例子就是(1 * 4) 匹配 (4,1), 批次为(10,4,2)
高维 * 高维时

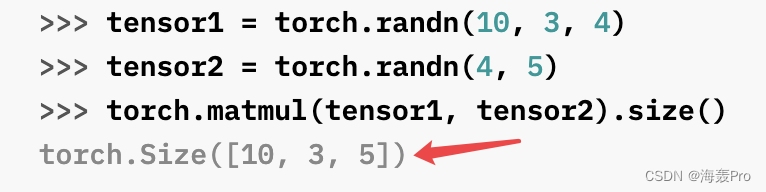
注:这不太好理解 … 感觉就是要找准批次,再进行乘法(靠感觉了 哈哈 离谱)
参考
结语
文章仅作为个人学习笔记记录,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

版权归原作者 海轰Pro 所有, 如有侵权,请联系我们删除。