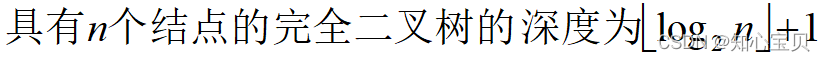C语言数据结构与算法-----树和二叉树全面总结（上）

一、前言

• 学习目标：理解树和二叉树的基本概念与性质、存储结构
• 重点：二叉树的五个性质、存储结构

二、树的概念和定义

• 定义：n(n>=0)个结点的有限集合，n=0，空树
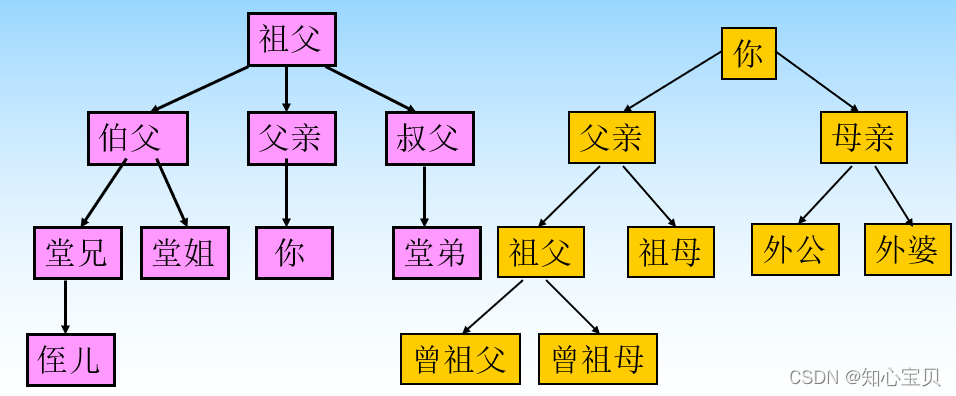
• 结点：表示树中的元素
• 根结点：第一个元素
• 叶结点：度为0，即没有子树
• 双亲结点：结点的直接前驱
• 孩子结点：结点的直接后继
• 兄弟结点：同一双亲结点的孩子
• 结点的度：结点的子树个数
• 结点的层次：根节点层次为1，依次向下加一
• 树的度：树中所有结点度的最大值
• 树的高度：树中所有结点层次的最大值
• 森林:m(m>=0)棵互不相交树的集合

例题：

求出下图的叶子结点、树的度、高度、结点B、C、D的度、H的兄弟和双亲、E的孩子

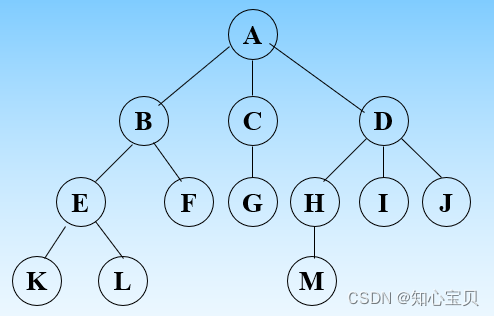
• 叶子结点：K、L、F、G、M、I、J
• 树的度和高度：3（最大结点的度数是D）、4
• 结点B、C、D的度：2、1、3
• H的兄弟和双亲、E的孩子：I、J D K、L

三、二叉树

1.基本概念

• 定义：满足每个结点度不大于2，孩子结点次序确定的树
• 左孩子：位于左侧
• 右孩子：位于右侧

2.基本形态

• n个结点有/（n+1）不同形态的二叉树

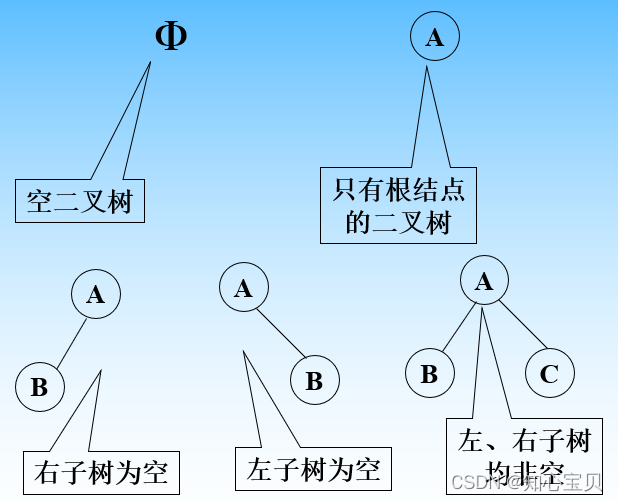
3.性质

1. 在二叉树的第i层上最多有 个结点(i>=1)
2. 深度为k的二叉树最多有 -1个结点(k>=1)
3. 对于任意一棵二叉树，度为0的结点数等于度为2的结点数+1
4. 
5. 结点为i双亲结点为i/2向下取整，左孩子2i，右孩子2i+1

4.满二叉树

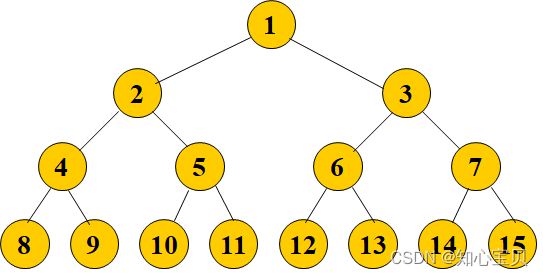
**特点： **

• 每一层的结点数都是最大结点数

5.完全二叉树

• 结点按照编号从左到右依次构建二叉树，不存在无左孩子、却有右孩子的情况
• 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

例题：

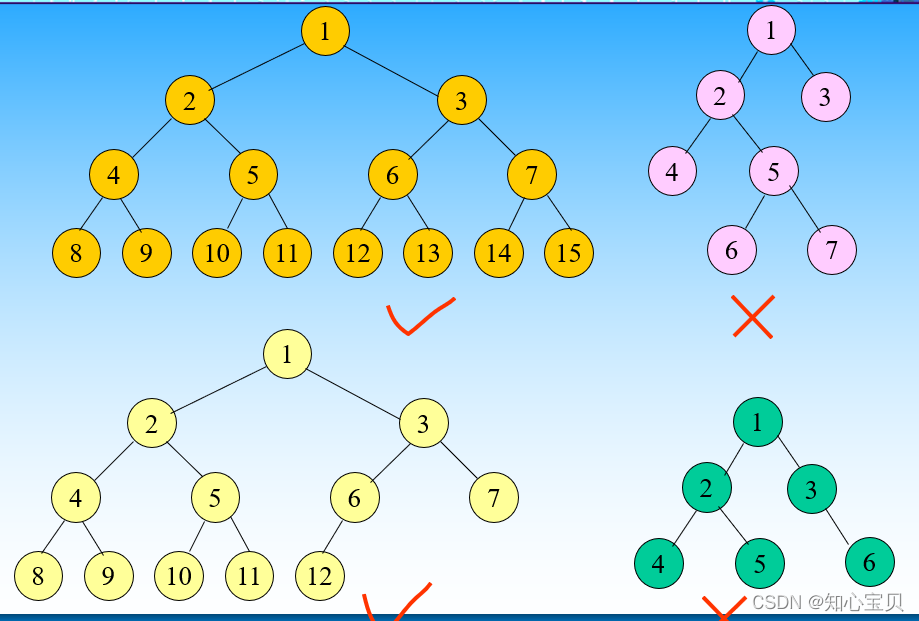
四、存储结构

1.顺序存储

• 实现：按照结点的层次编号，依次放入数组中，如上图编号的123456789
• 特点：结点间关系蕴含在其存储位置中、浪费空间，适于存满二叉树和完全二叉树

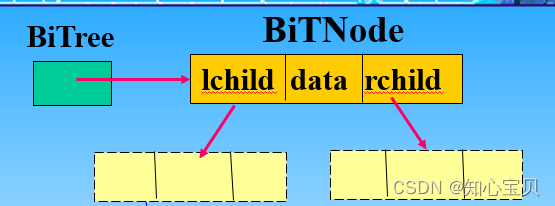
2.二叉链表

• lchild:指向左孩子结点，没有置为空
• rchild:指向右孩子结点，没有置为空
• 特点：在n个结点的二叉链表中，有n+1个指针域

结构体：

typedef  struct BiTNode
{    TElemType    data;
      struct BiTNode *lchild,  *rchild;
} BiTNode,*BiTree;

例：

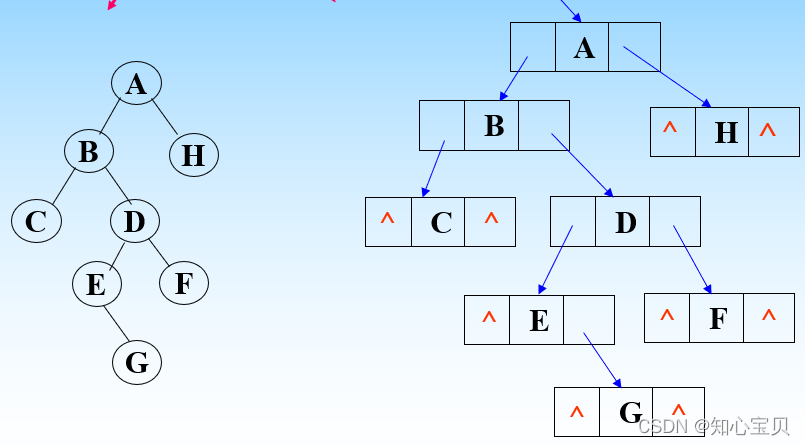
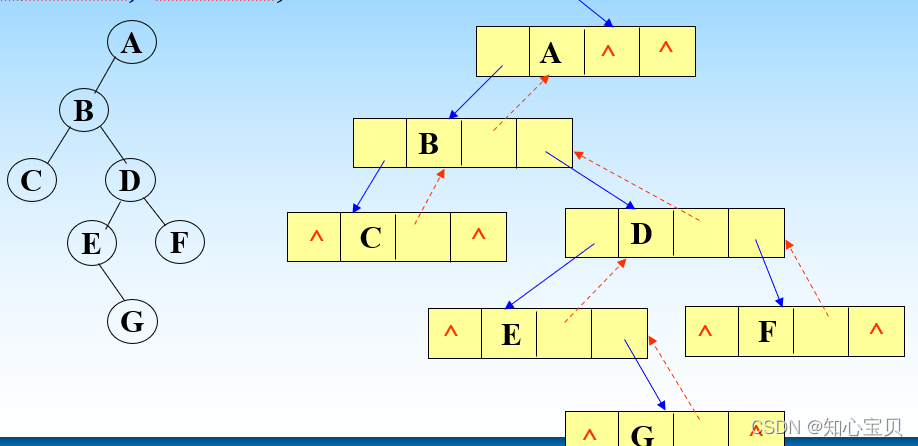
3.三叉链表

• 
• 定义：三叉链表就是有三个指针域，lchild指向左孩子，rchild指向右孩子和二叉链表一样，多出一个parent指向它的双亲结点

结构体：

typedef   struct  TriTNode
{ TElemType data;
      struct TriTNode  *lchild,  *rchild,  *parent;
} TriTNode,*TriTree;

例：

五、总结比较

线性结构树第一个数据元素(无前驱)
根结点(无前驱)

最后一个数据元素(无后继)
多个叶子结点(无后继)
其它数据元素(一个前驱、一个后继)

树中其它结点(一个前驱、多个后继)