旋转矩阵及左右乘的意义，看这一篇就够了

旋转矩阵及左右乘的意义，别浪费时间了，看这一篇就够了

前言

这些天研究旋转矩阵，被教科书和视频课绕迷糊了，可悲的是 ，如此简单的概念竟然没有一篇文章 （至少我没搜到）能够直观解释清楚，一气之下，我决定自己研究，经过不懈努力，终于解决了这一可爱又可恨的概念，也希望看到这篇文章的人能够静下心来好好阅读，对你肯定有帮助。

一、什么是旋转矩阵？

首先我需要花点儿时间说一下旋转矩阵的意义，大家一定一定要清楚旋转矩阵是有两个含义的：坐标变换和旋转向量，为了方便大家理解，我举最简单的例子。

1.坐标变换

如图所示，对于p点（或者叫向量），可以分别在不同坐标系下表示，红色坐标系绕黑色坐标系旋转了α角度：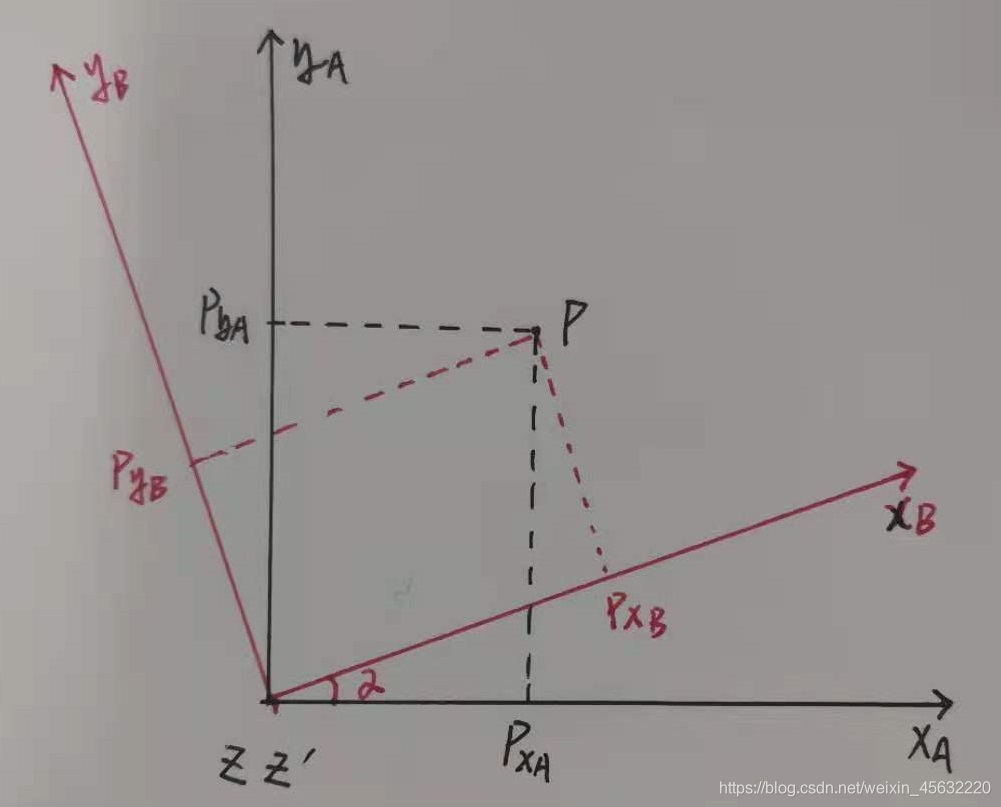

其坐标变换关系如下：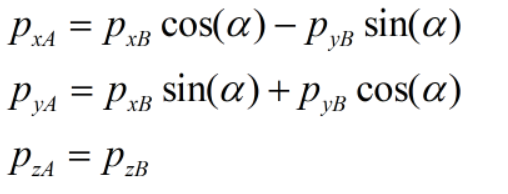

该变换关系由几何关系推导出，具体细节先不管，我们看上式写成矩阵形式是啥样：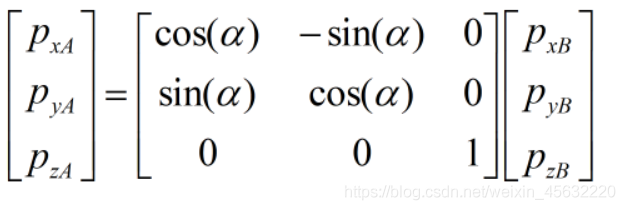

中间的2×2矩阵即为我们所说的旋转矩阵，这里特别要注意，这个矩阵的意义是将p点在旋转后的坐标系（红色）中的坐标，转换为旋转前的坐标系（黑色）中的坐标。

为什么会这样呢？从代数的角度出发最容易理解，请不要嫌麻烦，一步一步跟我来：
旋转矩阵的列向量：

可以看出，根据几何关系写出的旋转矩阵，其列向量恰好为旋转后坐标系（红色）的坐标轴在旋转前的坐标系（黑色）中的坐标，或者叫方向余弦。

也就是说，我想写出坐标系B相对于坐标系A的旋转矩阵，只需要将坐标系B相对于坐标系A的方向余弦写成矩阵的形式即可，如下图所示：

看到这个矩阵不要蒙，单独看其中一列，就是B坐标系的某一轴在A坐标系的X轴、Y轴和Z轴的投影，也就是我们所说的方向余弦，这里不做过多解释。

接着，我们把这个一般形式的全貌写出来：

取第一行，其实际运算的时候是这样：

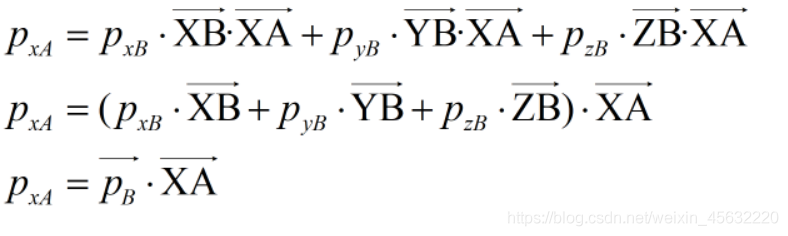
看最左侧，为p点（向量）在A坐标系下的x方向坐标，以此类推，旋转矩阵将p点在B坐标系下的坐标，转换为在A坐标系下的坐标。

2.向量旋转

旋转矩阵除了坐标变换的功能，还有一个功能就就是能够将向量旋转，这个我们仍然可以用代数的角度去考虑，
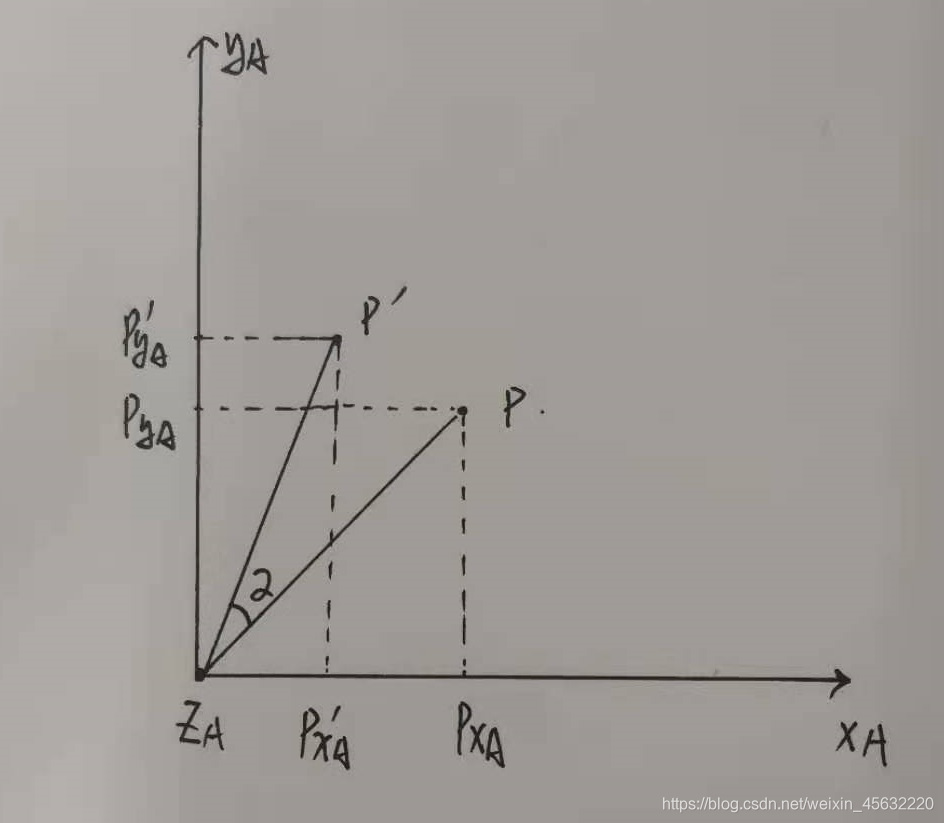
向量p经过旋转矩阵变换后变为p’，如图所示：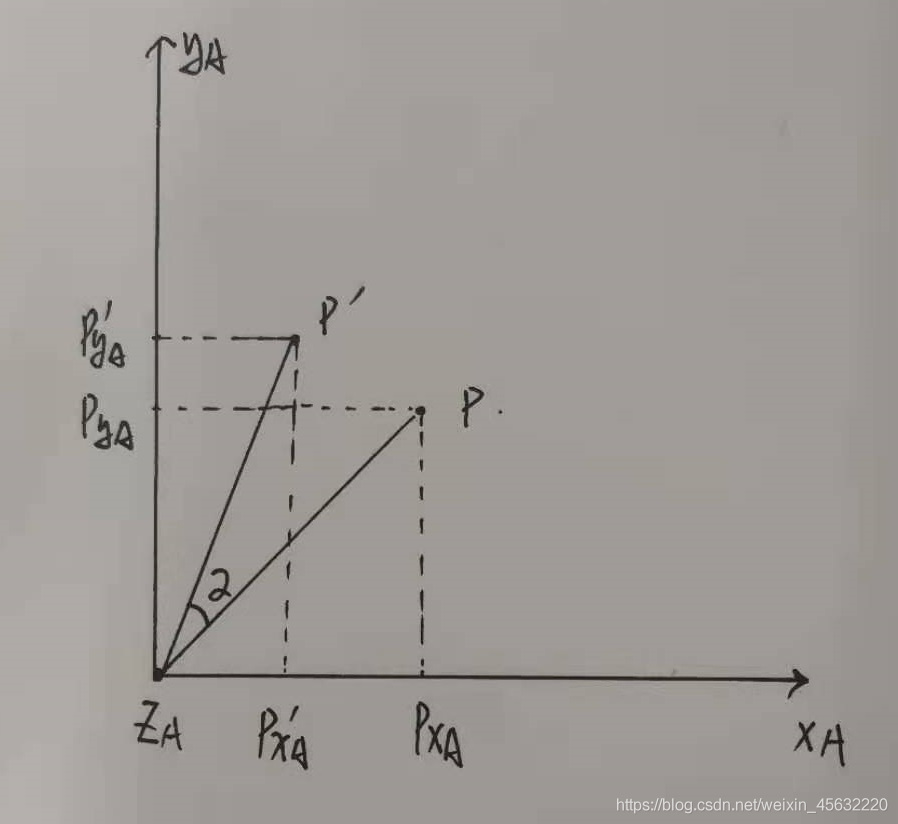

可以看出，原本的向量p经过与旋转矩阵相乘，变换到了新的p’位置，并且二者夹角为α。我可以很明确告诉你，这步操作的旋转矩阵同上一述坐标变换的旋转矩阵一样：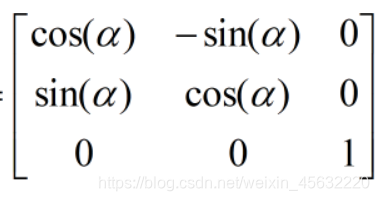

到这您可能会问了，同一旋转矩阵为何有两种功能呢？

好，看代数，上述操作可以写如下形式：

再看第一行：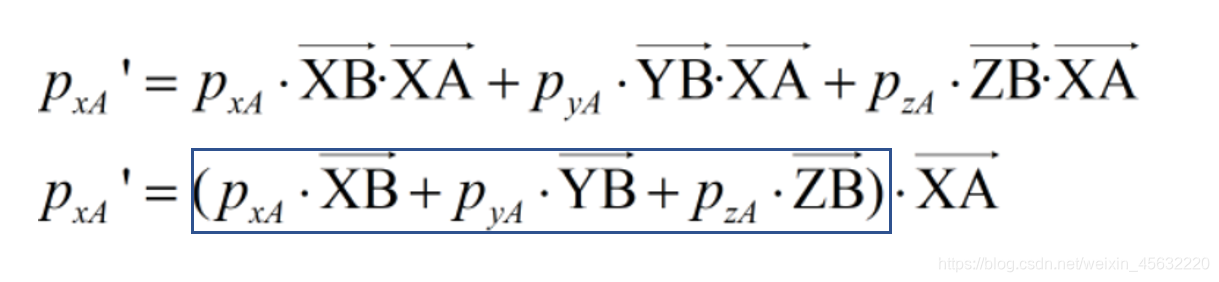

发现没有，蓝框里表示坐标系B中的一个向量，只不过该向量的坐标与坐标系A中的向量坐标相同。也就是说，旋转矩阵先将坐标系旋转，再在旋转后的坐标系上取与原坐标系坐标相同的向量，然后再将其投影到原坐标系，得到旋转后向量的坐标。

我想了很多话去形容这种操作，后来发现还是画图直观，请往下看：

画坐标系A和B，将坐标系B绕A旋转α角度：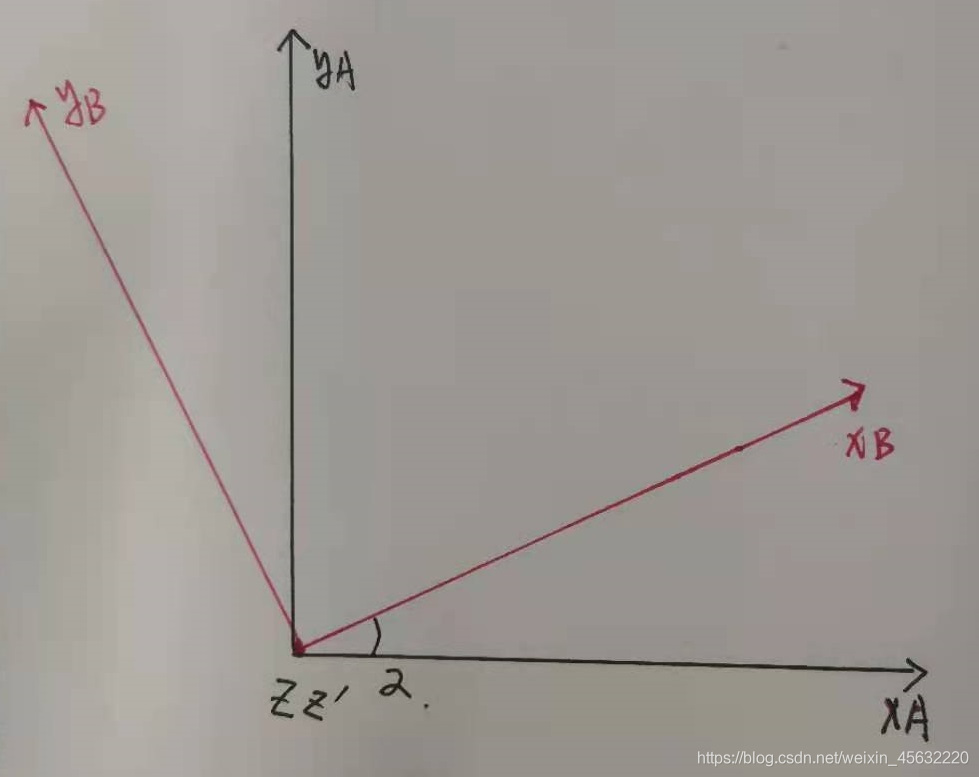

再在图中加一个点p，并标出坐标：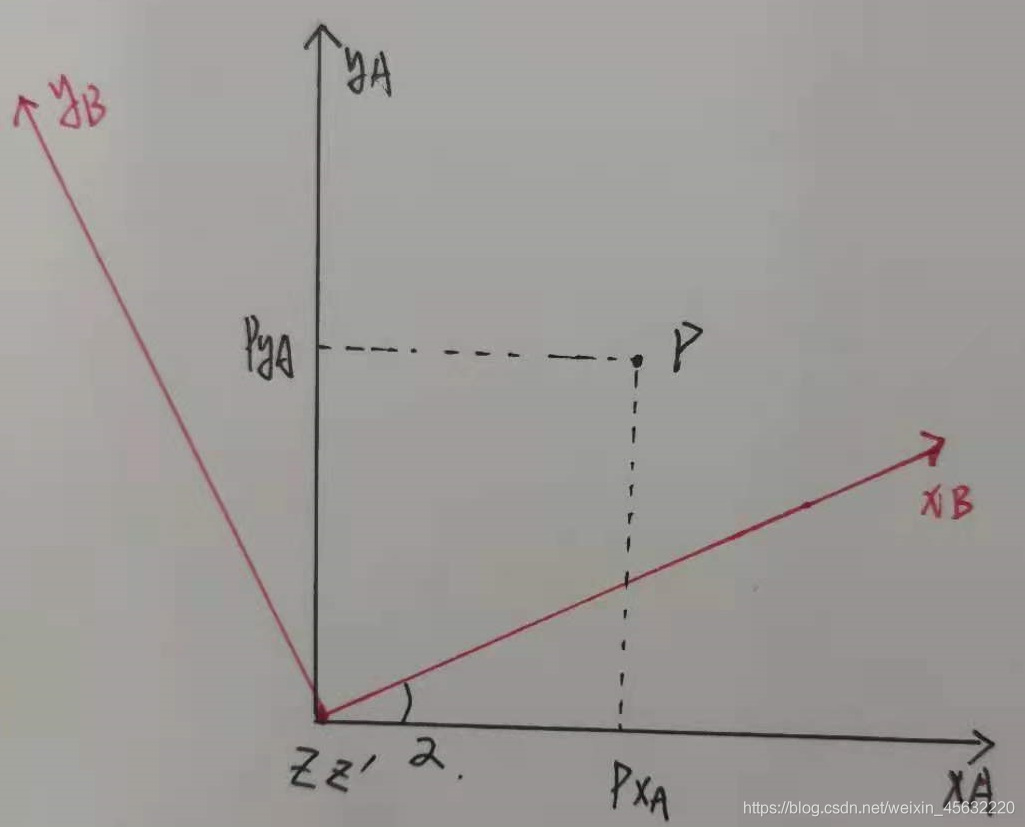

在坐标系B中取与坐标系A相同的坐标，画点，记为p‘，注意是相同的坐标：

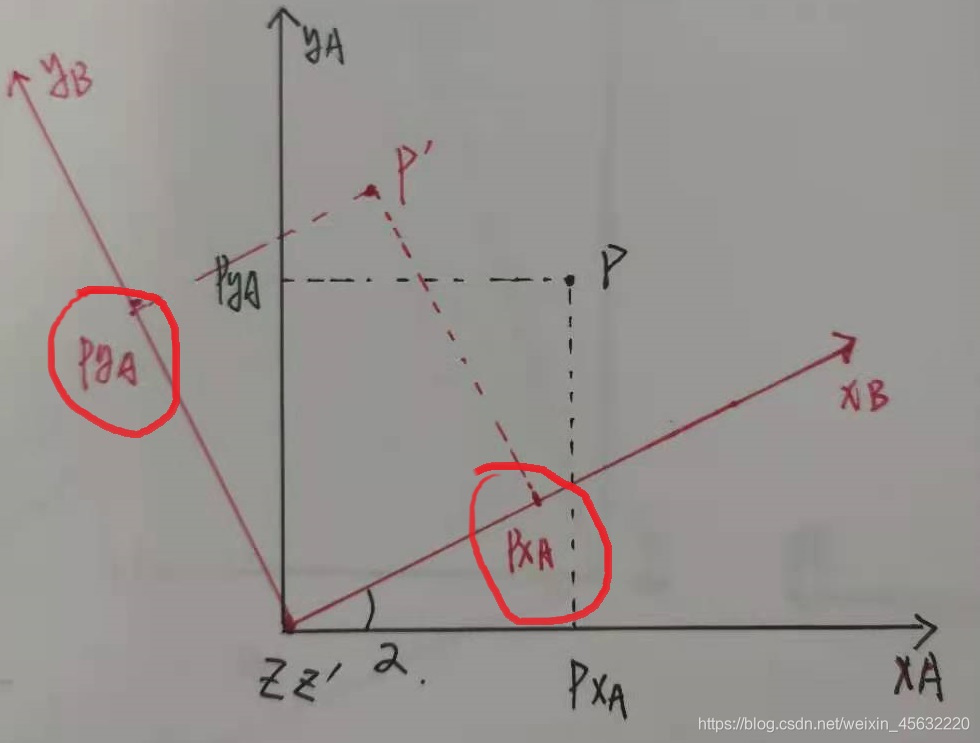
得到p‘点在A坐标系上的坐标：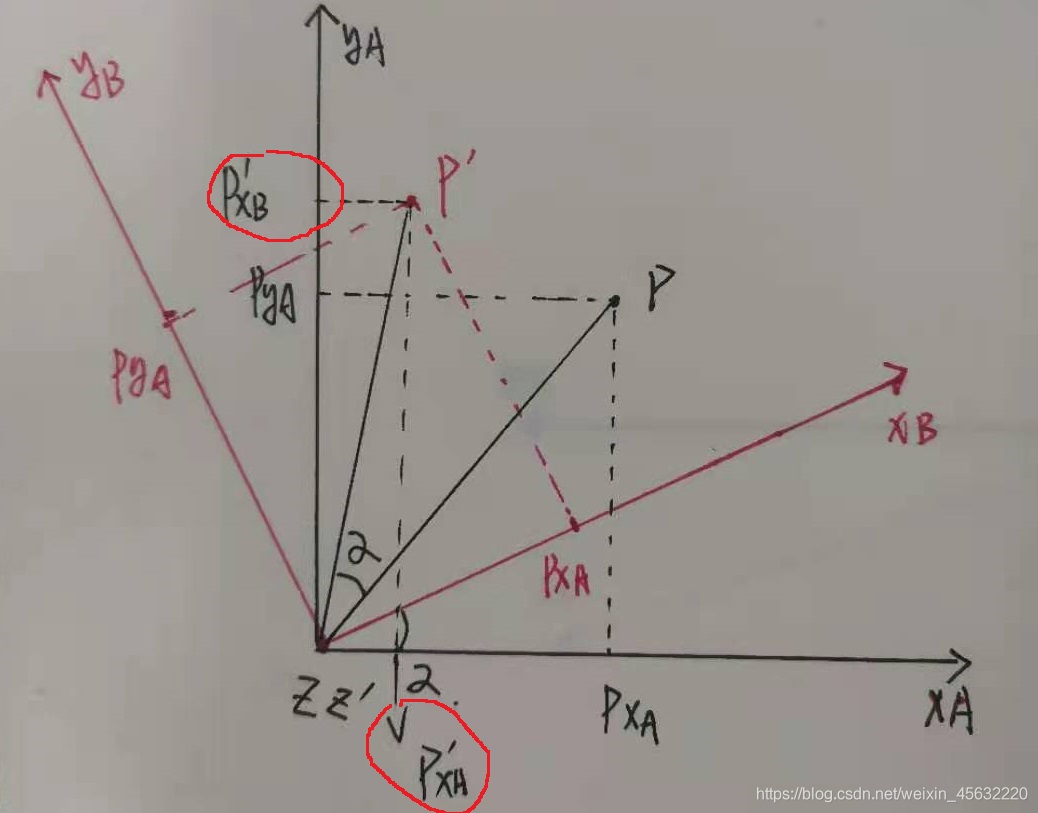

拿掉B坐标系，发现向量p发生了旋转，坐标系B仅起到中介作用，可以理解为向量p绕坐标系A转动了一定的角度：

至此，我想大家了解了旋转矩阵的两种功能，一个是坐标变换，一个是向量旋转，同样的旋转矩阵，同样的式子，就看你自己怎么解释了，这点来讲很重要，大家一定要清楚。

我知道到这里肯定还有人和我一样不是很懂，我再加以说明：

看这两个式子：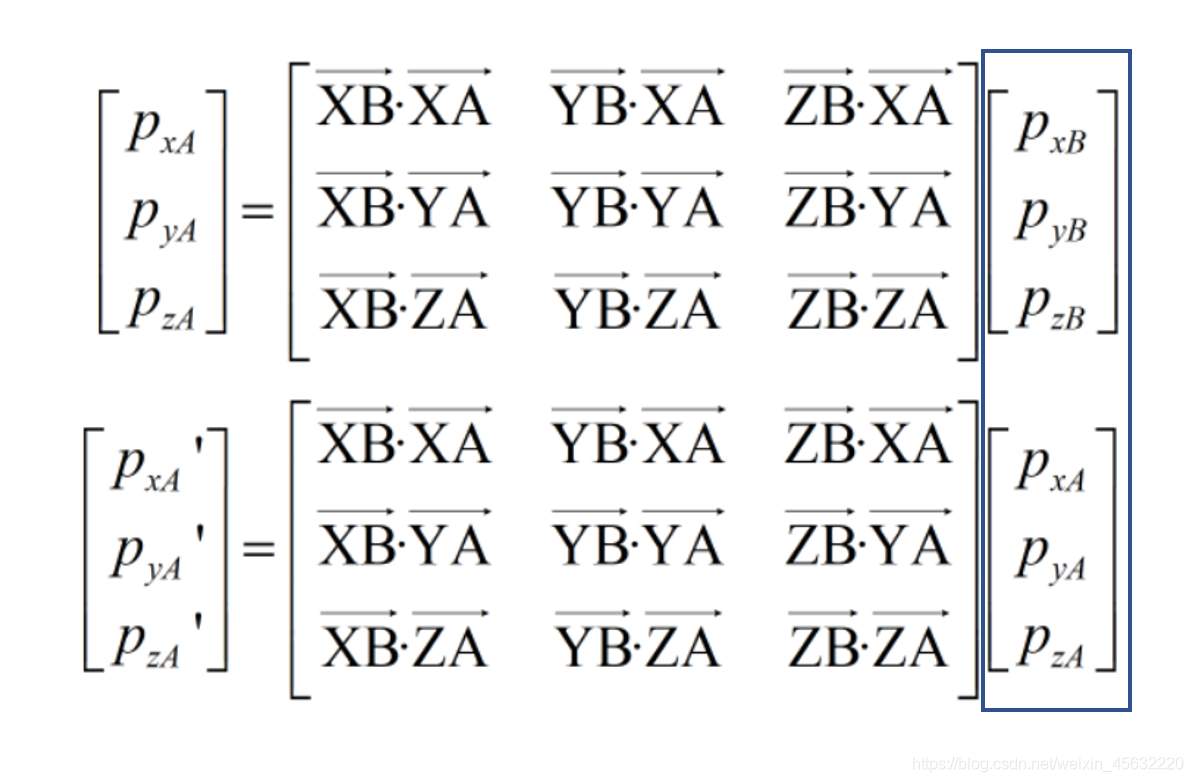

上面为坐标变换，下面为向量旋转，旋转矩阵肯定是一样了，那如果我右边蓝色方框中向量取的数值一样呢？那么左边数值是不是也一样？那左右数值的物理意义到底是什么呢？这就得看你怎么解释了，你解释成向量旋转也好，你解释成坐标变换也好，都可以。

二、矩阵的左右乘

可能大家都听到过，左乘旋转矩阵绕固定坐标系旋转，右乘旋转矩阵绕自身坐标系旋转。单纯记这句话很容易让人产生误解！首先，这里的左右乘指的并不是某一向量左乘或者右乘旋转矩阵，而是多个旋转矩阵的组合方式是左乘还是右乘。其次，这句话还遗漏了一个相当重要的信息，绕固定坐标系旋转讨论的是向量的旋转，绕自身坐标系旋转讨论的是坐标变换！这是完全不一样的两种功能，例如我想研究向量的旋转，我可以也只可以将其视为向量绕固定坐标系的旋转。往下看。

1.旋转矩阵左乘

我想要一个向量p0先绕x轴转α度，再绕y轴转β度，最后绕z轴转γ度，求旋转后向量的位置。
可见这是一个旋转矩阵组合的问题，之前讨论过，向量绕某一坐标轴旋转在数学上展现为向量左乘旋转矩阵，我们按照题意，当然是先让它绕x轴旋转：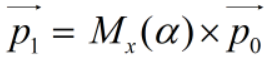

再绕y轴旋转：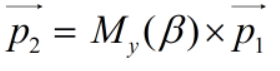

再绕z轴旋转，那么p3即为所求向量：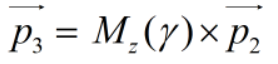

连起来就是：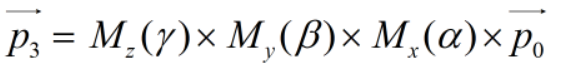

总的旋转矩阵R：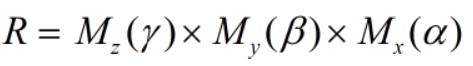

重点来了，让向量p0先后绕x、y、z轴旋转，其总的旋转矩R为绕x轴旋转的矩阵左乘绕y
轴旋转的矩阵再左乘绕z轴旋转的矩阵。
由此才引入的那句话，左乘绕固定坐标系旋转，现在我们来改一下，应该这么说 ：讨论向量旋转问题时，认为向量绕固定坐标轴旋转，旋转矩阵按旋转次序依次左乘，得到最终的旋转矩阵R。

2.旋转矩阵右乘

右乘讨论的就是坐标变换了，来看问题：已知在C坐标系下表示的向量pC，我想求pC在原始坐标系0下的表示p0，已知C坐标系由原始坐标系0绕轴X0旋转α度成为坐标系A，再绕轴YA旋转成为坐标系B，再绕轴ZB旋转成为坐标系C。

这里逻辑不通的就多琢磨一会儿，（脑补一下咋转的，这次是绕自身坐标系旋转）。

还记得之前那个图吗？我给你拿到这里来再看一下：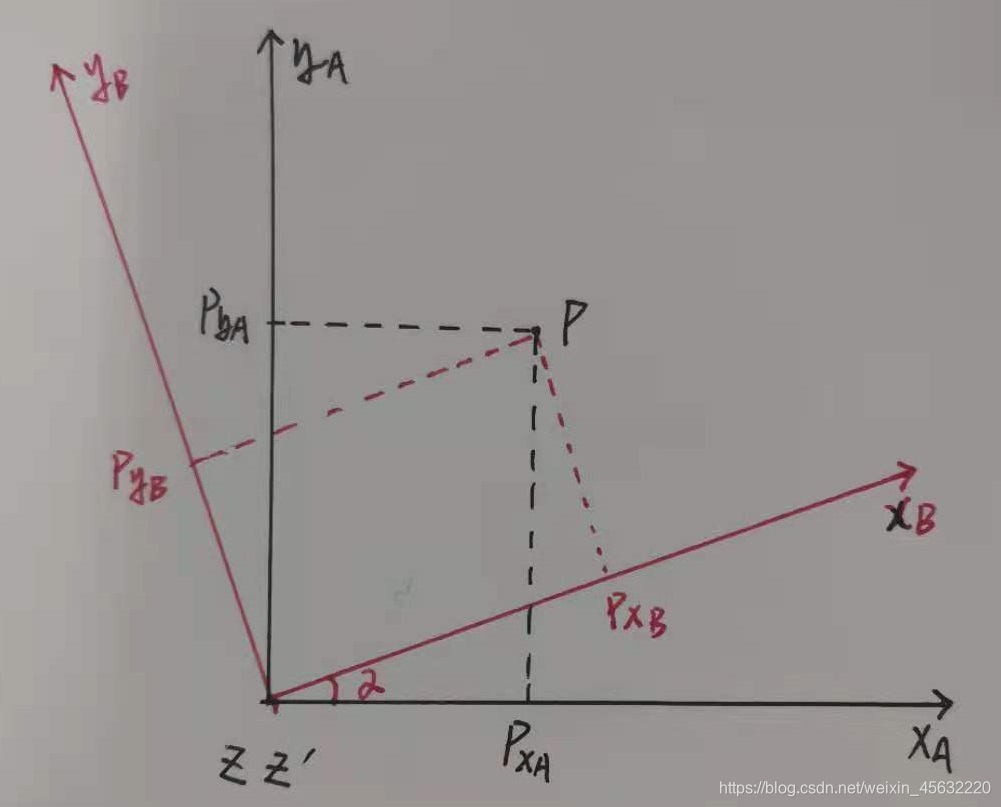

再复习一遍，p点在B坐标系下的坐标，乘以旋转矩阵，得到的是在A坐标系下的坐标，而B坐标系是由A坐标系转了α角转过去的，可以发现，这是一种“退回”效果，也就是p点在旋转后的坐标系下的坐标左乘旋转矩阵后，会变为旋转前坐标系下的坐标，这种效果表明旋转后的坐标系一定是绕旋转前坐标系的某一轴转过去的，对于旋转前的坐标系，可以理解为绕自身坐标系的坐标轴旋转后成了旋转后的坐标系。换句话说，因为你退回来得到的是前坐标系下的坐标，你转过去也必须是绕前坐标系中的坐标轴转过去的，故我们称之为绕自身坐标系旋转（感觉绕的话就多读两遍）这里一定要懂。

再回过来看，咱不是已知pC求p0吗，那咱们就一步一步往回退，退到坐标系0为止：
首先由坐标系C退回到坐标系B，（应该说p向量在C系中的表示变换为在B系中的表示）: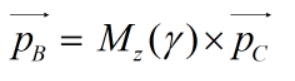

再由坐标系B退回到坐标系A: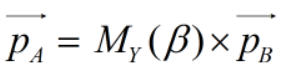

再由坐标系A退回到坐标系0：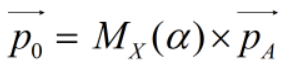

连起来为：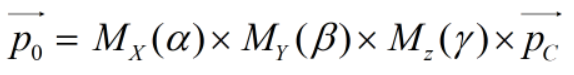

总的旋转矩阵R为：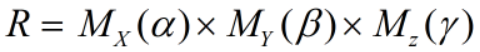

之前说过坐标系C是由坐标系0经过绕轴X0变为坐标系A，再绕轴YA变为坐标系B，再绕轴ZB旋转才得到的，为了使其退回去，看看旋转矩阵R的写法，是不是绕x轴旋转矩阵右乘y轴旋转旋转右乘z轴旋转矩阵？这就是我们所说的绕自身坐标轴旋转要右乘旋转矩阵。

总结

根据大数定律以及正态分布，我们大多数人的智商都处于人类的平均水平，可是精英教育不允许出现这种基础且冗长的讲解方式，晦涩难懂的课本、千篇一律的ppt、漫不经心的讲解是我们普通学生汲取知识的最大障碍，这就导致很大一部分人是看不懂课本跟不上课程的，csdn的出现或许能够为普通学生的学习搭建一个快速通道，我希望大家能共同努力，以尽可能通俗易懂的角度来说明问题，一起营造好的知识环境。
如有错误，请指正，如有好的概念，请补充。