目录
一、均方误差、精度与错误率
对模型的泛化性能进行评估,我们需要有衡量模型泛化能力的评价标准,这就是性能度量(Performance Measure)。
在评估同一个模型的泛化能力时,使用不同的性能度量往往会导致不同的评判结果,这意味着模型的 “好坏” 是相对的。什么样的模型是好的,不仅取决于算法和数据,还取决于性能度量。
在预测任务中,给定大小为
m
m
m 的数据集
D
=
{
(
x
1
,
y
1
)
,
⋯
,
(
x
m
,
y
m
)
}
D=\{(\boldsymbol{x}_1,y_1),\cdots,(\boldsymbol{x}_m,y_m)\}
D={(x1,y1),⋯,(xm,ym)}
其中
y
i
y_i
yi 是
x
i
\boldsymbol{x}_i
xi 的真实标记. 要评估模型
f
f
f 的性能,我们需要把预测结果
f
(
x
)
f(\boldsymbol{x})
f(x) 与真实标记
y
y
y 进行比较.
最简单的性能度量有以下三种:
- 均方误差(MSE): m s e ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 \displaystyle mse(f;D)=\frac1m \sum_{i=1}^m (f(\boldsymbol{x}_i)-y_i)^2 mse(f;D)=m1i=1∑m(f(xi)−yi)2;
- 精度(Accuracy): a c c ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) \displaystyle acc(f;D)=\frac1m \sum_{i=1}^m \mathbb{I}(f(\boldsymbol{x}_i)=y_i) acc(f;D)=m1i=1∑mI(f(xi)=yi);
- 错误率(Error): e r r ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) \displaystyle err(f;D)=\frac1m \sum_{i=1}^m \mathbb{I}(f(\boldsymbol{x}_i)\neq y_i) err(f;D)=m1i=1∑mI(f(xi)=yi).
其中
I
(
⋅
)
\mathbb{I}(\cdot)
I(⋅) 是指示函数,且精度和错误率满足如下关系
a
c
c
(
f
;
D
)
+
e
r
r
(
f
;
D
)
=
1
acc(f;D)+err(f;D)=1
acc(f;D)+err(f;D)=1
均方误差常用于回归任务,精度和错误率常用于分类任务。
sklearn.metrics
中提供了常见的性能度量,均方误差、精度和错误率的实现如下:
""" 均方误差 """from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred)""" 精度 """from sklearn.metrics import accuracy_score
acc = accuracy_score(y_true, y_pred)""" 错误率 """from sklearn.metrics import accuracy_score
err =1- accuracy_score(y_true, y_pred)
二、查准率、查全率与
F
1
F1
F1
2.1 查准率(Precision)与查全率(Recall)
错误率和精度虽然常用,但并不能满足所有的任务需求。
考虑这样一个场景,假定先前我们根据西瓜数据集训练出了一个能够判断好瓜还是坏瓜的模型。现在又有一车新的西瓜,我们用训练好的模型对这些西瓜进行判别,自然地,错误率衡量了有多少比例的瓜被判断错误。
但如果我们关心的是:
- 挑出来的瓜(模型判断出的好瓜)有多少比例是真的好瓜。
- 所有真的好瓜中有多少比例被挑了出来(模型判断为好瓜)。
那么错误率显然就不够用了,因此有必要引入新的性能度量。
上面几句话似乎有些绕口,接下来我们再用几张图去形象地阐释一遍。
假定瓜农拉来的一车西瓜如下(只有6个):

西瓜上方是它的编号,下方是它的真实标签。我们用学得的模型
f
f
f 对这六个西瓜的判断结果如下:

可以看出,编号为
1
,
2
,
5
1,2,5
1,2,5 的西瓜都被判断错误了,因此错误率为
3
/
6
=
0.5
3/6=0.5
3/6=0.5,精度也为
0.5
0.5
0.5.
- 挑出来的瓜(即模型判断出的好瓜)为 2 , 4 , 5 , 6 2,4,5,6 2,4,5,6,这四个被挑出来的瓜只有 4 4 4 和 6 6 6 是真的好瓜,占比 0.5 0.5 0.5。
- 所有真的好瓜为 1 , 4 , 6 1,4,6 1,4,6,这三个真的好瓜中,只有 4 4 4 和 6 6 6 被挑出来了(即模型判断为好瓜),占比 0.67 0.67 0.67。
接下来可以定义查准率和查全率了,不过在此之前,我们有必要引入混淆矩阵(Confusion Matrix)。
对于二分类问题,可将样例根据其真实类别与模型预测的类别组合划分为四类:
T P TP TP(True Positive):真实标记为**正**,预测标记也为**正**。F P FP FP(False Positive): 真实标记为**负**,但预测标记为**正**。T N TN TN(True Negative):真实标记为**负**,预测标记也为**负**。F N FN FN(False Negative):真实标记为**正**,但预测标记为**负**。
显然有
T
P
+
F
P
+
T
N
+
F
N
=
m
TP+FP+TN+FN=m
TP+FP+TN+FN=m. 分类结果的混淆矩阵形式如下:
[
T
N
F
P
F
N
T
P
]
\begin{bmatrix} TN & FP \\ FN& TP \\ \end{bmatrix}
[TNFNFPTP]
我们的查准率(Precision)与查全率(Recall)分别定义为:
P
=
T
P
T
P
+
F
P
,
R
=
T
P
T
P
+
F
N
P=\frac{TP}{TP+FP},\quad R=\frac{TP}{TP+FN}
P=TP+FPTP,R=TP+FNTP
例如,对于之前我们举的例子,查准率和查全率分别为
P
=
0.5
,
R
=
0.67
P=0.5,\quad R=0.67
P=0.5,R=0.67
现在计算混淆矩阵:
- 真的好瓜,且被模型判断为好瓜的是 4 4 4 和 6 6 6,因此 T P = 2 TP=2 TP=2;
- 真的坏瓜,且被模型判断为好瓜的是 2 2 2 和 5 5 5,因此 F P = 2 FP=2 FP=2;
- 真的好瓜,且被模型判断为坏瓜的是 1 1 1,因此 F N = 1 FN=1 FN=1;
- 对于最后一个,我们可以直接套用公式,即 T N = 6 − T P − F P − F N = 1 TN=6-TP-FP-FN=1 TN=6−TP−FP−FN=1;
从而混淆矩阵为
[
1
2
1
2
]
\begin{bmatrix} 1 & 2 \\ 1& 2 \\ \end{bmatrix}
[1122]
不难看出,查准率与查全率适用于分类任务,相应的实现如下:
""" 查准率 """from sklearn.metrics import precision_score
precision = precision_score(y_true, y_pred)""" 查全率 """from sklearn.metrics import recall_score
recall = recall_score(y_true, y_pred)
对于本节一开始的例子,我们记好瓜为
1
1
1,坏瓜为
0
0
0,则:
from sklearn.metrics import precision_score, recall_score, accuracy_score
y_true =[1,0,0,1,0,1]
y_pred =[0,1,0,1,1,1]print(accuracy_score(y_true, y_pred))# 0.5print(precision_score(y_true, y_pred))# 0.5print(recall_score(y_true, y_pred))# 0.6666666666666666
结果与我们原先的计算相符。
2.2 混淆矩阵的可视化
对于二分类问题,我们的混淆矩阵是一个
2
×
2
2\times 2
2×2 矩阵。进而可知,对于
N
N
N 分类问题,我们的混淆矩阵是一个
N
×
N
N\times N
N×N 矩阵。
sklearn.metrics
中提供了计算混淆矩阵的函数:
confusion_matrix()
。我们依然使用 2.1 节中的例子,使用
confusion_matrix()
来计算相应的混淆矩阵:
from sklearn.metrics import confusion_matrix
y_true =[1,0,0,1,0,1]
y_pred =[0,1,0,1,1,1]
C = confusion_matrix(y_true, y_pred)print(C)# [[1 2]# [1 2]]
输出结果与我们 2.1 节中计算的相同。
对于多分类问题,
confusion_matrix()
返回的混淆矩阵
C
C
C 满足:
C
i
j
C_{ij}
Cij 代表真实类别为
i
i
i 但却被模型预测为类别
j
j
j 的样例个数。
为了更好的展示混淆矩阵,我们考虑三分类问题,相应的
y_true
和
y_pred
设置为:
y_true =[2,0,2,2,0,1]
y_pred =[0,0,2,2,0,2]
现在使用
ConfusionMatrixDisplay()
来实现混淆矩阵的可视化
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import matplotlib.pyplot as plt
y_true =[2,0,2,2,0,1]
y_pred =[0,0,2,2,0,2]
C = confusion_matrix(y_true, y_pred)
disp = ConfusionMatrixDisplay(C)
disp.plot()
plt.show()

2.3 P-R曲线与BEP
查准率和查全率是一对矛盾的度量。一般来说,查准率高时,查全率往往偏低;查全率高时,查准率往往偏低。通常只有在一些简单的任务中,才可能使得查准率和查全率都很高。
回到 2.1 节中的例子,我们根据西瓜数据集训练出来的模型本质上是一个二分类器。事实上,许多二分类器的原理,就是设置一个阈值,然后对每一个样例进行打分,分数大于等于该阈值的样例被分为正类,分数小于该阈值的样例被分为负类。
例如,设置阈值为
0.5
0.5
0.5,对于一个新样本(西瓜),若它的得分高于
0.5
0.5
0.5,则被认为是好瓜,否则认为是坏瓜。
事实上,上述提到的精度、查准率、查全率全都依赖于具体的阈值。有些时候,我们希望不固定阈值,而是根据实际需求去调整。
依然使用 2.1 节中的例子,假定阈值就是
0.5
0.5
0.5,我们的二分类器对于六个样例的打分情况如下:

我们根据这六个西瓜的得分将它们从高到低进行排序:
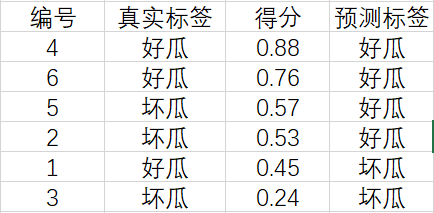
现在,我们从上往下遍历。对于第一行的样例,设它的得分
0.88
0.88
0.88 为阈值,**大于等于**该阈值的预测为正例,**小于**该阈值的预测为反例,相应的结果如下:

计算可得查准率和查全率分别为
P
=
1
,
R
=
0.33
P=1,\, R=0.33
P=1,R=0.33.
对于第二行的样例,设它的得分
0.76
0.76
0.76 为阈值,**大于等于**该阈值的预测为正例,**小于**该阈值的预测为反例,相应的结果如下:

计算可得查准率和查全率分别为
P
=
1
,
R
=
0.67
P=1,\, R=0.67
P=1,R=0.67.
以此类推,我们最终可以得到
6
6
6 个
(
R
,
P
)
(R, P)
(R,P) 值。代码实现如下:
from sklearn.metrics import precision_score, recall_score
y_true =[1,1,0,0,1,0]for i inrange(len(y_true)):
y_pred =[1]*(i +1)+[0]*(len(y_true)- i -1)
P = precision_score(y_true, y_pred)
R = recall_score(y_true, y_pred)print((R, P))
输出结果:
(0.3333333333333333, 1.0)
(0.6666666666666666, 1.0)
(0.6666666666666666, 0.6666666666666666)
(0.6666666666666666, 0.5)
(1.0, 0.6)
(1.0, 0.5)
我们将这六个点连起来绘制曲线:
from sklearn.metrics import precision_score, recall_score
import matplotlib.pyplot as plt
y_true =[1,1,0,0,1,0]
R, P =[],[]for i inrange(len(y_true)):
y_pred =[1]*(i +1)+[0]*(len(y_true)- i -1)
P +=[precision_score(y_true, y_pred)]
R +=[recall_score(y_true, y_pred)]
plt.plot(R, P)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()

上图称为 P-R图,其中的曲线称为 P-R曲线。
P-R曲线的进一步讨论:首先我们记真实标记为正和负的样例个数分别为
m
+
m^+
m+ 和
m
−
m^-
m−,即
m
+
=
T
P
+
F
N
,
m
−
=
T
N
+
F
P
m^+=TP+FN,\quad m^-=TN+FP
m+=TP+FN,m−=TN+FP
查准率与查全率可以写为
P
=
T
P
T
P
+
F
P
,
R
=
T
P
m
+
P=\frac{TP}{TP+FP},\quad R=\frac{TP}{m^+}
P=TP+FPTP,R=m+TP
现在考虑更一般的情形,我们将
m
m
m 个西瓜的得分(之前是六个西瓜的得分)**从高到低**进行排列得到一个**有序列表**:
s
c
o
r
e
=
[
h
1
h
2
⋮
h
m
]
\mathrm{score}= \begin{bmatrix} h_1 \\ h_2 \\ \vdots \\ h_m \end{bmatrix}
score=⎣⎢⎢⎢⎡h1h2⋮hm⎦⎥⎥⎥⎤
设阈值为
h
h
h,当
h
>
h
1
h>h_1
h>h1 时,所有西瓜都会被预测为坏瓜,即没有一个西瓜会被预测成好瓜,所以
T
P
=
F
P
=
0
TP=FP=0
TP=FP=0,此时
P
=
0
/
0
P=0/0
P=0/0**无意义**,所以我们接下来的讨论都将基于
h
≤
h
1
h\leq h_1
h≤h1。一般而言,我们会把阈值
h
h
h 分别设置为每一个样例的得分,从而会有
m
m
m 种阈值。
我们先取最小的阈值,即
h
=
h
m
h=h_m
h=hm,那么所有的瓜都会被预测成好瓜,即没有一个瓜会被预测成坏瓜,所以
T
N
=
F
N
=
0
TN=FN=0
TN=FN=0,此时有
T
P
=
m
+
TP=m^+
TP=m+ 和
F
P
=
m
−
FP=m^-
FP=m−,从而
R
=
1
R=1
R=1 且
P
=
m
+
/
(
m
+
+
m
−
)
=
m
+
/
m
P=m^+/(m^++m^-)=m^+/m
P=m+/(m++m−)=m+/m,这反映在P-R曲线上**最后一个点**的坐标为
(
1
,
m
+
m
)
\Big(1,\frac{m^+}{m}\Big)
(1,mm+)
如果
(
1
,
m
+
/
m
)
→
(
1
,
0
)
(1,m^+/m)\to(1,0)
(1,m+/m)→(1,0),则有
m
+
≪
m
m^+\ll m
m+≪m,因此
m
−
≫
0
m^-\gg0
m−≫0,结合上述的
T
N
=
0
TN=0
TN=0,这说明**样本中有大量的反例,且它们都被预测错误了**。又因为
F
N
=
0
FN=0
FN=0,说明**样本中有少量的正例,且它们都被预测正确了**。从而可知,如果P-R曲线的最后一个点趋于
(
1
,
0
)
(1,0)
(1,0),那么样本分布**极其不均衡**(有着极多的反例和极少的正例),且分类器对于**反例全部预测错误**,对于**正例全部预测正确**,因此这种P-R曲线对应的分类器**很糟糕**。
我们再取最大的阈值,即
h
=
h
1
h=h_1
h=h1,那么只有第一个西瓜会被预测为好瓜,剩余的西瓜都被预测为坏瓜。我们分以下两种情况讨论:
- 第一个西瓜本身就是好瓜,那么 T P = 1 TP=1 TP=1, F P = 0 FP=0 FP=0,从而 P = 1 P=1 P=1, R = 1 / m + R=1/m^+ R=1/m+,P-R曲线上第一个点的坐标为 ( 1 / m + , 1 ) (1/m^+,1) (1/m+,1);
- 第一个西瓜本身就是坏瓜,那么 F P = 1 FP=1 FP=1, T P = 0 TP=0 TP=0,从而 P = R = 0 P=R=0 P=R=0,P-R曲线上第一个点的坐标为 ( 0 , 0 ) (0, 0) (0,0)。
大多数情况下我们的数据集规模都比较大,即
m
+
≫
0
m^+\gg0
m+≫0。所以,**当得分最高的样例为正例时**,P-R曲线上第一个点的坐标**非常接近**
(
0
,
1
)
(0,1)
(0,1) 但不等于
(
0
,
1
)
(0,1)
(0,1);**当得分最高的样例为反例时**,P-R曲线上第一个点的坐标**是**
(
0
,
0
)
(0,0)
(0,0)。
更直观地来讲,假设每一个
h
i
h_i
hi**都只对应一个瓜**,当我们将
h
h
h 从
h
1
h_1
h1 依次下调至
h
m
h_m
hm 时,相应的P-R曲线会依次从第一个点绘制到最后一个点。当
h
h
h 从
h
i
−
1
h_{i-1}
hi−1 下调至
h
i
h_i
hi 时,若
h
i
h_i
hi 所对应的瓜本身是正例,则
T
P
↑
TP \uparrow
TP↑,
F
P
FP
FP 不变,
F
N
↓
FN \downarrow
FN↓,从而
P
↑
P\uparrow
P↑,
R
↑
R\uparrow
R↑,这反映在P-R曲线将会产生一条**向右上方**的线段。若
h
i
h_i
hi 所对应的瓜本身是反例,则
F
P
↑
FP\uparrow
FP↑,
T
P
TP
TP 不变,
F
N
FN
FN 也不变,从而
P
↓
P\downarrow
P↓,
R
R
R 不变,这反映在P-R曲线将会产生一条**竖直向下**的线段。
综合以上讨论可得出: 我们从
(
0
,
0
)
(0,0)
(0,0) 或
(
1
/
m
+
,
1
)
(1/m^+,1)
(1/m+,1) 开始,根据有序列表依次下调阈值。每当经过一个正例,我们绘制一条斜向右上的线段;每当经过一个反例,我们绘制一条竖直向下的线段。如此进行下去直到抵达
(
1
,
m
+
/
m
)
(1, m^+/m)
(1,m+/m),此时P-R曲线绘制完毕。
从绘制过程可以看出,我们的P-R曲线是呈锯齿状的,且呈 “下降” 趋势。
当然,
sklearn.metrics
中提供了绘制P-R曲线的函数,我们将真实标签列表
y_true
和 得分列表
y_score
传入
precision_recall_curve()
中可得到查准率、查全率和阈值,如下:
from sklearn.metrics import precision_recall_curve
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
precision, recall, thresholds = precision_recall_curve(y_true, y_score)print(precision)# [0.6 0.5 0.66666667 1. 1. 1. ]print(recall)# [1. 0.66666667 0.66666667 0.66666667 0.33333333 0. ]print(thresholds)# [0.45 0.53 0.57 0.76 0.88]
然后使用
PrecisionRecallDisplay()
来进行绘制:
from sklearn.metrics import precision_recall_curve, PrecisionRecallDisplay
import matplotlib.pyplot as plt
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
precision, recall, _ = precision_recall_curve(y_true, y_score)
disp = PrecisionRecallDisplay(precision, recall)
disp.plot()
plt.show()

可能会有读者疑惑,为什么这里的曲线和我们之前自己绘制的曲线不一样,并且为什么
thresholds
中只有五个阈值呢?
我们先不用
PrecisionRecallDisplay()
,只用
precision_recall_curve()
得到的结果去绘制:
from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
precision, recall, _ = precision_recall_curve(y_true, y_score)
plt.plot(recall, precision)
plt.show()

可以看出这张图和上一张图相比,仅仅是连线的方式有所改变。
PrecisionRecallDisplay()
中取消了斜向右上的这种连线方式,为了美观起见采用 “横平竖直” 的方式去绘制,我们再来看一下
PrecisionRecallDisplay()
中
plot()
函数的部分源码:
defplot(self, ax=None,*, name=None,**kwargs):...
line_kwargs ={"drawstyle":"steps-post"}...(self.line_,)= ax.plot(self.recall, self.precision,**line_kwargs)...return self
"step-post"
这一参数说明了P-R曲线将采用阶梯形式进行绘制,详情见文档。
在上面的三张P-R图中,我们已经知道了第二张图和第三张图仅仅是绘制方式的不同,接下来我们将第三张图和第一张图进行比较。
可以看到,相比于第一张图,第三张图去掉了最后一个点,并且在第一个点的前面加上了
(
0
,
1
)
(0,1)
(0,1) 这个点,这种做法的用意何在呢?
我们先来看下
precision_recall_curve()
的源码:
defprecision_recall_curve(y_true, probas_pred, pos_label=None, sample_weight=None):
fps, tps, thresholds = _binary_clf_curve(y_true, probas_pred,
pos_label=pos_label,
sample_weight=sample_weight)
precision = tps /(tps + fps)
precision[np.isnan(precision)]=0
recall = tps / tps[-1]# stop when full recall attained# and reverse the outputs so recall is decreasing
last_ind = tps.searchsorted(tps[-1])
sl =slice(last_ind,None,-1)return np.r_[precision[sl],1], np.r_[recall[sl],0], thresholds[sl]
从
return
一行可以看出
(
0
,
1
)
(0,1)
(0,1) 这个点是**强行**加上去的,那原先P-R曲线上的最后一个点为什么会被去掉呢?
注意到这一行注释:
# stop when full recall attained
即当
R
=
1
R=1
R=1 时停止计算,而我们的第一张图的最后两个点的横坐标**都为**
1
1
1,因此最后一个点不会被计算,相应的最低阈值也不会添加进
thresholds
中。
事实上可以证明,如果得分最低的样例是反例,则最后两个点的横坐标都为
1
1
1;如果得分最低的样例是**正例**,则**倒数第二个点**的横坐标为
1
−
1
/
m
+
1-1/m^+
1−1/m+。
至于为什么
(
0
,
1
)
(0,1)
(0,1) 会被强行添加至P-R曲线中,是因为
sklearn
想让P-R曲线从
y
y
y 轴开始绘制。
为了方便接下来的叙述,我们将P-R曲线绘制成单调平滑的曲线(注意,现实任务中的P-R曲线通常是非单调,不平滑的,在很多局部有上下波动,可参考上图),如下图:
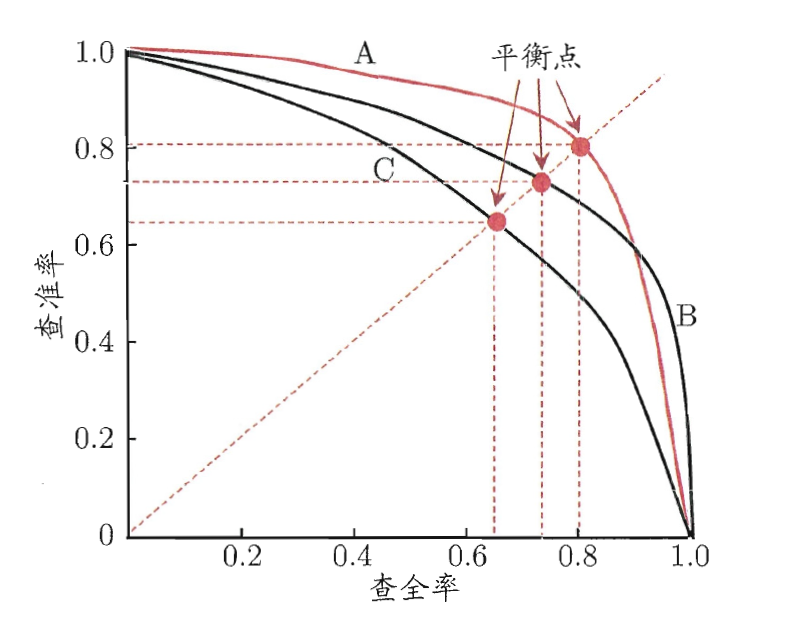
P-R 图直观地展示了分类器在样本总体上的查全率与查准率。在进行比较时,若一个分类器的P-R曲线被另一个分类器的曲线完全包住,则可断言后者的性能优于前者。例如,上图中
B
B
B 的性能要优于
C
C
C。
如果两个分类器的P-R曲线发生交叉,例如上图中的
A
A
A 和
B
B
B,这时一个比较合理的判据是比较**P-R曲线下面积的大小**,它在一定程度上表征了分类器在查准率和查全率上取得相对 “双高” 的比例,但这个值不容易估算,因此需要设计一些能综合考察查准率和查全率的性能度量。
平衡点(Break-Even Point,简称BEP)就是这样一种度量,它是
P
=
R
P=R
P=R 时的取值。对于本节一开始提到的例子,其平衡点为
0.67
0.67
0.67。
2.4
F
1
F1
F1 与
F
β
F_{\beta}
Fβ
上述提到的BEP过于简化了一些,我们更常用的是
F
1
F1
F1 度量,它是基于查准率和查全率的**调和平均**定义的:
1
F
1
=
1
2
(
1
P
+
1
R
)
\frac{1}{F1}=\frac12\left(\frac1P+\frac1R\right)
F11=21(P1+R1)
化简得到
F
1
=
2
⋅
P
⋅
R
P
+
R
F1=\frac{2\cdot P\cdot R}{P+R}
F1=P+R2⋅P⋅R
在一些应用中,我们对查准率和查全率的重视程度有所不同,因此需要引入
F
1
F1
F1 度量的一般形式——
F
β
F_{\beta}
Fβ,它能让我们表达出对查准率
/
/
/查全率的不同偏好。它定义为查准率和查全率的**加权调和平均**:
1
F
β
=
1
1
+
β
2
(
1
P
+
β
2
R
)
,
β
>
0
\frac{1}{F_{\beta}}=\frac{1}{1+\beta^2}\left(\frac1P+\frac{\beta^2}{R}\right),\quad \beta>0
Fβ1=1+β21(P1+Rβ2),β>0
化简得到
F
β
=
(
1
+
β
2
)
⋅
P
⋅
R
β
2
⋅
P
+
R
,
β
>
0
F_{\beta}=\frac{(1+\beta^2)\cdot P\cdot R}{\beta^2\cdot P+R},\quad \beta>0
Fβ=β2⋅P+R(1+β2)⋅P⋅R,β>0
β = 1 \beta=1 β=1, F β F_{\beta} Fβ 退化为 F 1 F1 F1;β > 1 \beta>1 β>1,查全率有更大影响;β < 1 \beta<1 β<1,查准率有更大影响。
F
1
F1
F1 与
F
β
F_{\beta}
Fβ 是适用于**分类任务**的性能度量,相应的实现如下:
""" F1 """from sklearn.metrics import f1_score
f1 = f1_score(y_true, y_pred)""" Fbeta """from sklearn.metrics import fbeta_score
fbeta = fbeta_score(y_true, y_pred, beta=0.5)# 以beta=0.5为例
三、ROC与AUC
3.1 ROC(Receiver Operating Characteristic)
此前我们已经提到,对
m
m
m 个样例的得分从高到低排序可以得到一个有序列表。在不同的应用任务中,我们可根据任务需求来设置不同的**阈值**(截断点)。若更重视查准率,则可在列表中靠前的位置进行截断;若更重视查全率,则可在列表中靠后的位置进行截断。
因此,排序本身质量的好坏,体现了综合考虑学习器在不同任务下的期望泛化性能的好坏,ROC曲线则是从这个角度出发来研究学习器泛化性能的有力工具。
ROC全称是 受试者工作特征(Receiver Operating Characteristic),它源于二战中用于敌机检测的雷达信号分析技术,此后被引入机器学习领域中。
ROC曲线与P-R曲线很相似。在P-R曲线中,纵坐标采用的是查准率,横坐标采用的是查全率,但在ROC曲线中,纵坐标采用的是真正例率(True Positive Rate,简称TPR),横坐标采用的是假正例率(False Positive Rate,简称FPR),两者分别定义为
T
P
R
=
T
P
T
P
+
F
N
=
R
,
F
P
R
=
F
P
T
N
+
F
P
TPR=\frac{TP}{TP+FN}=R,\quad FPR=\frac{FP}{TN+FP}
TPR=TP+FNTP=R,FPR=TN+FPFP
我们将诸
(
F
P
R
,
T
P
R
)
(FPR,TPR)
(FPR,TPR) 点用线段连接起来就得到了ROC曲线。
sklearn.metrics
中提供了实现ROC曲线的函数
roc_curve()
,相应的用法如下:
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
fpr, tpr, _ = roc_curve(y_true, y_score)
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()

当然我们也可以直接用
RocCurveDisplay()
来快速绘制:
from sklearn.metrics import roc_curve, RocCurveDisplay
import matplotlib.pyplot as plt
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
fpr, tpr, _ = roc_curve(y_true, y_score)
disp = RocCurveDisplay(fpr=fpr, tpr=tpr)
disp.plot()
plt.show()
输出结果和上图是一致的。
从图中可以看出,ROC曲线也呈锯齿状,且每一段都是横平竖直的。此外,ROC曲线呈 “上升” 趋势,它的第一个点和最后一个点一定会分别位于
(
0
,
0
)
(0,0)
(0,0) 和
(
1
,
1
)
(1,1)
(1,1)。学习器的性能越好,ROC曲线越接近图中的左上角。
设当前阈值所对应的点为
(
x
,
y
)
(x,y)
(x,y),我们依次下调阈值。当经过一个正例时,下一个点的坐标为
(
x
,
y
+
1
/
m
+
)
(x,y+1/m^+)
(x,y+1/m+);当经过一个反例时,下一个点的坐标为
(
x
+
1
/
m
−
,
y
)
(x+1/m^-,y)
(x+1/m−,y)。
3.2 AUC(Area Under roc Curve)
在进行学习器的比较时,与P-R图相似,若一个学习器的ROC曲线被另一个学习器的曲线完全包住,则可断言后者的性能优于前者。如果两个学习器的ROC曲线发生交叉,那么我们就要比较ROC曲线下的面积,即AUC(Area Under roc Curve),如下图所示

假定ROC曲线是由坐标为
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
m
,
y
m
)
(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)
(x1,y1),(x2,y2),⋯,(xm,ym) 的按序连接形成,其中
(
x
1
,
y
1
)
=
(
0
,
0
)
,
(
x
m
,
y
m
)
=
(
1
,
1
)
(x_1,y_1)=(0,0),\,(x_m,y_m)=(1,1)
(x1,y1)=(0,0),(xm,ym)=(1,1),则AUC为
A
U
C
=
∑
i
=
1
m
−
1
(
x
i
+
1
−
x
i
)
⋅
y
i
+
1
+
y
i
2
\mathrm{AUC}=\sum_{i=1}^{m-1}(x_{i+1}-x_i)\cdot \frac{y_{i+1}+y_i}{2}
AUC=i=1∑m−1(xi+1−xi)⋅2yi+1+yi
sklearn.metrics
中的
auc()
就是根据上述公式进行计算的,相应代码如下:
from sklearn.metrics import roc_curve, auc
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
fpr, tpr, _ = roc_curve(y_true, y_score)print(auc(fpr, tpr))# 0.7777777777777778
但上面这种做法需要先计算出横纵坐标
fpr
、
tpr
,更快捷的方法是使用
roc_auc_score()
:
from sklearn.metrics import roc_auc_score
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]print(roc_auc_score(y_true, y_score))# 0.7777777777777778
如果我们想要在ROC曲线图上显示AUC,则需要将AUC传入
RocCurveDisplay()
中的
roc_auc
中:
from sklearn.metrics import roc_curve, RocCurveDisplay, auc
import matplotlib.pyplot as plt
y_true =[1,0,0,1,0,1]
y_score =[0.45,0.53,0.24,0.88,0.57,0.76]
fpr, tpr, _ = roc_curve(y_true, y_score)
roc_auc = auc(fpr, tpr)
disp = RocCurveDisplay(fpr=fpr, tpr=tpr, roc_auc=roc_auc)
disp.plot()
plt.show()
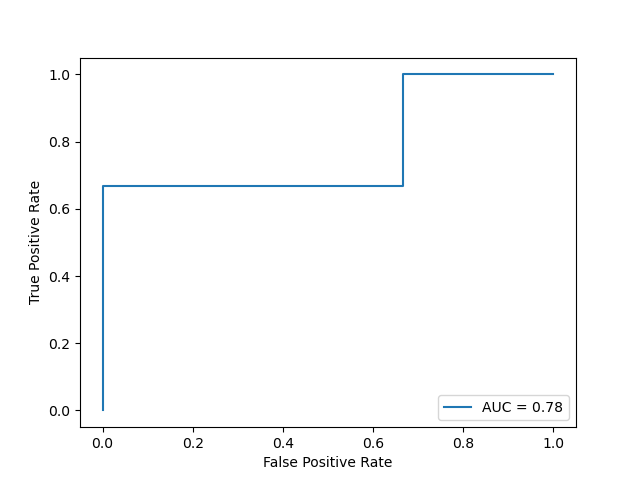
AUC的进一步讨论:忽略不同样例得分相同的情形,令
D
+
D^+
D+ 和
D
−
D^-
D− 分别表示正、反例集合,且
∣
D
+
∣
=
m
+
,
∣
D
−
∣
=
m
−
|D^+|=m^+,\, |D^-|=m^-
∣D+∣=m+,∣D−∣=m−,则AUC可以表示成:
A
U
C
=
1
m
+
m
−
∑
x
+
∈
D
+
∑
x
−
∈
D
−
I
[
f
(
x
+
)
>
f
(
x
−
)
]
\mathrm{AUC}=\frac{1}{m^+m^-}\sum_{\boldsymbol{x}^+\in D^+}\sum_{\boldsymbol{x}^-\in D^-}\mathbb{I}[f(\boldsymbol{x}^+)>f(\boldsymbol{x}^-)]
AUC=m+m−1x+∈D+∑x−∈D−∑I[f(x+)>f(x−)]
从上面的表达式可以看出,AUC实际上反应了样本中一个正例得分大于一个负例得分的概率,即样本预测的排序质量。
定义排序损失为
ℓ
r
a
n
k
=
1
m
+
m
−
∑
x
+
∈
D
+
∑
x
−
∈
D
−
I
[
f
(
x
+
)
<
f
(
x
−
)
]
\ell_{rank}=\frac{1}{m^+m^-}\sum_{\boldsymbol{x}^+\in D^+}\sum_{\boldsymbol{x}^-\in D^-}\mathbb{I}[f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-)]
ℓrank=m+m−1x+∈D+∑x−∈D−∑I[f(x+)<f(x−)]
容易看出
A
U
C
+
ℓ
r
a
n
k
=
1
\mathrm{AUC}+\ell_{rank}=1
AUC+ℓrank=1,即
ℓ
r
a
n
k
\ell_{rank}
ℓrank 是ROC曲线上方的面积。
References
[1] 机器学习.周志华
[2] Metrics and scoring: quantifying the quality of predictions.
[3] 11565 P-R、ROC、DET 曲线及 AP、AUC 指标全解析(上).
[4] sklearn’s precision_recall_curve incorrect on small example.
[5] sklearn precision_recall_curve and threshold.
[6] How does sklearn select threshold steps in precision recall curve?
版权归原作者 serity 所有, 如有侵权,请联系我们删除。