1.二叉树的结构定义
typedefchar Elemtype;//二叉树的结构定义typedefstructcsNode{
Elemtype data;structcsNode*lchild;structcsNode*rchild;} Csnode,*tree;
2.二叉树的建立
//二叉树的建立voidCreatTree(tree &T)//引用传参 {char ch;
cin>>ch;if(ch=='#')
T=NULL;else{
T=new Csnode;if(!T)return;(T)->data=ch;printf("请输入%c的左子树: ",ch);CreatTree((T)->lchild);printf("请输入%c的右子树: ",ch);CreatTree((T)->rchild);}}
3.复制二叉树
//复制二叉树/*****如果是空树,递归结束
else,申请新节点空间复制根节点,
递归复制左子树
递归复制右子树*/intCopy(tree T,tree&NewT){if(T==NULL){
NewT=NULL;return0;}else{
NewT=new Csnode;
NewT->data=T->data;Copy(T->lchild,NewT->lchild);Copy(T->rchild,NewT->rchild);}}
4.前序遍历算法
//前序遍历算法voidPreCreat(tree T){if(T==NULL)return;
cout<<T->data<<" ";PreCreat(T->lchild);PreCreat(T->rchild);}
5.中序遍历算法
//中序遍历算法voidMidCreat(tree T){if(T==NULL)return;MidCreat(T->lchild);
cout<<T->data<<" ";MidCreat(T->rchild);}
6.后序遍历算法
//后序遍历算法voidRearCreat(tree T){if(T==NULL)return;RearCreat(T->lchild);RearCreat(T->rchild);
cout<<T->data<<" ";}
7.计算二叉树的深度
//计算二叉树的深度intdepth(tree T){int m,n;if(T==NULL)return0;else{
m=depth(T->lchild);
n=depth(T->rchild);if(m>n)return(m+1);elsereturn(n+1);}}
8.计算二叉树中的结点总数
//计算二叉树中的结点总数//如果是空树,返回0,//else,节点个数=左子树结点个数加右子树节点个数+1;intNodeCnt(tree T){if(T==NULL)return0;elsereturnNodeCnt(T->lchild)+NodeCnt(T->lchild)+1;}
9.计算叶子节点的个数
//计算叶子节点的个数/*****如果为空树,则叶子节点为0
******else, 叶子节点个数=左子树叶子结点个数加右子树叶子节点个数;*/intleafCnt(tree T){if(T==NULL)return0;if(T->lchild==NULL&&T->rchild==NULL)return1;elsereturnNodeCnt(T->lchild)+NodeCnt(T->lchild);}
10.测试案例
#include<iostream>usingnamespace std;typedefchar Elemtype;//二叉树的结构定义typedefstructcsNode{
Elemtype data;structcsNode*lchild;structcsNode*rchild;} Csnode,*tree;//二叉树的建立voidCreatTree(tree &T)//引用传参 {char ch;
cin>>ch;if(ch=='#')
T=NULL;else{
T=new Csnode;if(!T)return;(T)->data=ch;printf("请输入%c的左子树: ",ch);CreatTree((T)->lchild);printf("请输入%c的右子树: ",ch);CreatTree((T)->rchild);}}//复制二叉树/*****如果是空树,递归结束
else,申请新节点空间复制根节点,
递归复制左子树
递归复制右子树*/intCopy(tree T,tree&NewT){if(T==NULL){
NewT=NULL;return0;}else{
NewT=new Csnode;
NewT->data=T->data;Copy(T->lchild,NewT->lchild);Copy(T->rchild,NewT->rchild);}}//前序遍历算法voidPreCreat(tree T){if(T==NULL)return;
cout<<T->data<<" ";PreCreat(T->lchild);PreCreat(T->rchild);}//中序遍历算法voidMidCreat(tree T){if(T==NULL)return;MidCreat(T->lchild);
cout<<T->data<<" ";MidCreat(T->rchild);}//后序遍历算法voidRearCreat(tree T){if(T==NULL)return;RearCreat(T->lchild);RearCreat(T->rchild);
cout<<T->data<<" ";}//计算二叉树的深度intdepth(tree T){int m,n;if(T==NULL)return0;else{
m=depth(T->lchild);
n=depth(T->rchild);if(m>n)return(m+1);elsereturn(n+1);}}//计算二叉树中的结点总数//如果是空树,返回0,//else,节点个数=左子树结点个数加右子树节点个数+1;intNodeCnt(tree T){if(T==NULL)return0;elsereturnNodeCnt(T->lchild)+NodeCnt(T->lchild)+1;}//计算叶子节点的个数/*****如果为空树,则叶子节点为0
******else, 叶子节点个数=左子树叶子结点个数加右子树叶子节点个数;*/intleafCnt(tree T){if(T==NULL)return0;if(T->lchild==NULL&&T->rchild==NULL)return1;elsereturnNodeCnt(T->lchild)+NodeCnt(T->lchild);}intmain(){printf("请输入第一个节点的数据:\n");
tree T;CreatTree(T);
cout<<"前序遍历:";PreCreat(T);
cout<<"\n中序遍历:";MidCreat(T);
cout<<"\n后序遍历:";RearCreat(T);
cout<<"\n该二叉树的深度为:"<<depth(T)<<endl;
cout<<"\n该二叉树的结点个数为:"<<NodeCnt(T)<<endl;
cout<<"\n该二叉树的叶子结点个数为:"<<leafCnt(T)<<endl;
cout<<"复制二叉树:"<<endl;
tree NewT;Copy(T,NewT);
cout<<"复制后二叉树的前序遍历:";PreCreat(NewT);
cout<<"\n复制后二叉树的中序遍历:";MidCreat(NewT);
cout<<"\n复制后二叉树的后序遍历:";RearCreat(NewT);}
测试结果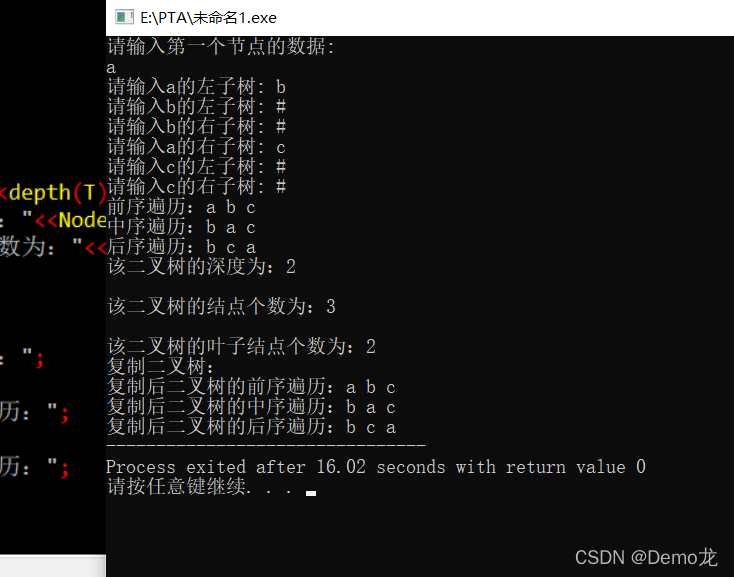
本文转载自: https://blog.csdn.net/qq_59708493/article/details/122785529
版权归原作者 Demo龙 所有, 如有侵权,请联系我们删除。
版权归原作者 Demo龙 所有, 如有侵权,请联系我们删除。