0
0

第四部分 供应链库存的计划和管理(二)供应链的不确定性管理:安全库存

一、安全库存在供应链中的作用

    **安全库存(safe inventory)**是指为了满足超出预期水平的顾客需求而持有的库存。之所以持有安全库存，是因为需求和供应的不确定性。如果实际需求超过预测需求或者供应晚于预期，则可能导致产品短缺。

    供应链管理者在设置安全库存时**必须进行权衡**。一方面，提高安全库存水平能够提高产品可获性，从而从顾客购买中获利；另一方面，提高安全库存水平回增加库存持有成本。

    **产品多样性的增加以及提高产品可获性的压力，促使企业提高所持有的安全库存水平。**在大多数高科技 产品的供应链中，由于产品多样性和需求高度不确定性，安全库存在库存中所占的比例非常高。

    因此，**供应链成功的关键**是，在不损害产品可获性的前提下，找到降低安全库存水平的有效途径。

    对于任何一条供应链来说，在设置安全库存时，都需要考虑一下三个重要问题：

            1.合理的产品可获性水平应该为多少？

            2.要达到希望的产品可获性水平，需要设置多少安全库存？

            3.在不影响产品可获性的前提下，可以采取哪些措施来减少安全库存？

    第一个问题将在下一篇文章进行讨论，本文回答第二和第三个问题(假定希望的产品可获性水平已确定)。

二、影响安全库存水平的因素

    合理的安全库存水平由以下因素决定：

           ** -期望的产品可获性水平**

** -需求的不确定性**

** -供给的不确定性**

** -库存补货策略**

    前三个因素与安全库存水平成正比。

1.产品可获性的度量

    产品可获性反映了企业用现有库存来满足顾客订单的能力。如果顾客订单到达而企业没有存货，就出现了**缺货(stockout)。**有许多方法可以用来度量产品可获性。以下列出了反应产品可获性的重要度量指标。

    (1)**产品满足率(product fill rate , fr)**是指利用库存满足的产品需求的比例，也就是利用现有库存满足产品需求的可能性。产品满足率应以特定的需求量而非时间为基准来测算。

    (2)**订单满足率(order fill rate)**是指利用现有库存满足的订单的比例。同样，订单满足率也应以以特定的订单数量而非时间为基准来测算。

    (3)**周期服务水平(cycle service level,CSL)**是指所有顾客需求都得到满足的补货周期所占的比例。**补货周期(replenishment cycle)**是指连续两次补货交付之间的时间间隔。

    在单一产品的情况下，产品满足率和订单满足率之间的差别并不明显。然而，当企业经销多种产品时，两者的差异可能十分显著。

2.需求不确定性的度量

    假设周期性需求服从均值为D、标准差为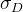![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)的正态分布。

D：每期的平均需求

\sigma _{D}：每期需求的标准差(预测误差)

    虽然需求的标准差并不一定就等于预测误差，但是在我们讨论中把两者是为可以互换。**事实上，安全库存的计算应该是建立在预测误差的基础上。**

** 提前期(lead time)**是指从发出订单到订货到达之间的时间间隔。在本文，用L来表示提前期。如果已知提前期为一固定值L且已知每个时期的需求分布，就可以估计出L个时期的需求分布。

估计L个时期的需求分布

    假设第i期(i=1,2,...,L)的产品需求服从均值为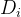![D_{i}](https://latex.csdn.net/eq?D_%7Bi%7D)、标准差为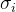![\sigma _{i}](https://latex.csdn.net/eq?%5Csigma%20_%7Bi%7D)的正太分布。用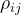![\rho _{ij}](https://latex.csdn.net/eq?%5Crho%20_%7Bij%7D)表示第i期和第j期的需求相关系数。这样，L个时期的总需求服从均值为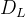![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)、标准差为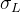![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)的正态分布，其中：


     若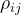![\rho _{ij}](https://latex.csdn.net/eq?%5Crho%20_%7Bij%7D)=1,表示两个时期的需求完全正相关。若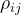![\rho _{ij}](https://latex.csdn.net/eq?%5Crho%20_%7Bij%7D)=-1，则两个时期的需求完全负相关。若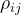![\rho _{ij}](https://latex.csdn.net/eq?%5Crho%20_%7Bij%7D)=0，则两个时期的需求相互独立。假设L个时期内每个时期的需求都相互独立，且都服从均值为D、标准差为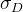![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)的正太分布。那么从上式可看出，L个时期的总需求总均值为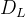![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)、标准差为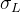![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)的正态分布，其中：


     不确定性的另一个重要度量指标是**变异系数(cv)**，它是标准差与均值之比。假设需求的均值为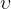![\upsilon](https://latex.csdn.net/eq?%5Cupsilon)，标准差为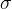![\sigma](https://latex.csdn.net/eq?%5Csigma)，那么

c\upsilon =\sigma /\mu

   变异系数用于衡量不确定性相对于需求的程度大小。

3.供给不确定性的度量

    供给不确定性主要表现在订单未能按时送达或订单中所订产品未能全部送达。假设用提前期的不确定性来描述供给的不确定性。也就是说，假设订货全数送达但是货物送达的时点是不确定的。假设提前期服从L，标准差为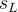![s_{L}](https://latex.csdn.net/eq?s_%7BL%7D)的正态分布。

L：平均提前期

s_{L}：提前期的标准差

估计提前期不确定时的需求分布

    假设第i期的产品需求服从均值为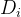![D_{i}](https://latex.csdn.net/eq?D_%7Bi%7D)、标准差为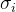![\sigma _{i}](https://latex.csdn.net/eq?%5Csigma%20_%7Bi%7D)的正态分布且各期需求相互独立。假设提前期服从均值为L，标准差为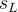![s_{L}](https://latex.csdn.net/eq?s_%7BL%7D)的正态分布。那么，提前期(不确定的)内的总需求服从均值为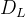![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)、标准差为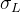![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)的正态分布，其中：


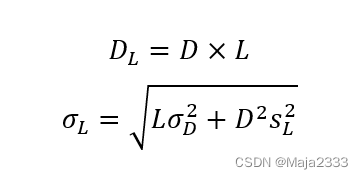
     可以看到，相较于提前期为固定值的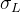![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)，提前期的不确定性使得提前期内需求的标准差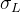![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)增大。

4.补货策略

    这里介绍两种补货策略：

    (1)**连续盘点(continuous review)**:这种方法是随时检查库存，当库存下降至再订货点(reorder point,ROP)时，就发出批量为Q的订货。

    (2)**周期盘点(periodic review)**:这种方法是按照预先规定的时间间隔定期对库存进行盘点，并随即提出补货，将库存水平补充到指定目标库存水平。

三、确定合理的安全库存水平

    本文仅关注连续盘点的情况。连续盘点的策略是，当库存下降至再订货点时，按订货批量Q进行补货。假设每周的需求服从均值为D、标准差为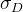![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)的正态分布，补货提前期为L周。

1.安全库存与周期服务水平

计算给定再订货点时的安全库存

    假设提前期为L周，且平均周需求为D，可得：


     则

计算给定再订货点时的周期服务水平

    提前期为L周，每周的需求服从均值为D，标准差为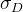![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)的正态分布。注意到，当提前期的需求大于ROP时，补货周期内就会有缺货发生。因此：


     前面假设提前期内的需求服从正态分布，且均值为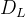![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)，标准差为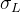![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)。CSL可表示如下：

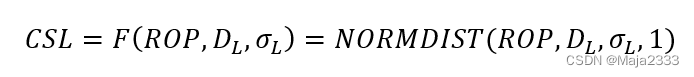
2.计算给定期望周期服务水平下所需的安全库存

给定期望周期服务水平下所需安全库存的计算

    假设需求服从正态分布，且需求相互独立。假定已知以下的变量：

期望周期服务水平=CSL

提前期内的平均需求=D_{L}

提前期内需求的标准差=\sigma _{L}

    由前面可知，ROP=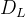![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)+ss。要确定合理的安全库存，以使下式成立：


     假设需求服从正太分布，必须确定合理的安全库存，以使下式成立：


     根据正态分布函数的反函数的定义可得：


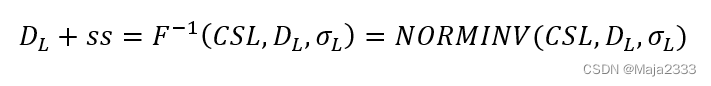
     或


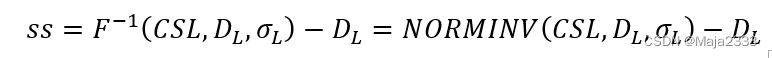
     同样可得，

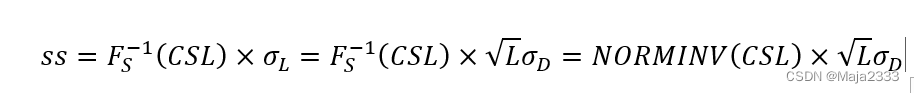
3.安全库存与满足率

计算给定再订货点时的满足率

    补货周期平均预期缺货率(ESC)表示每个补货周期内无法由现有库存满足的那部分市场需求的平均值。假设订货批量为Q(这也是一个补货周期内的平均需求)，那么需求流失率就等于ESC/Q。因此，满足率可计算如下：


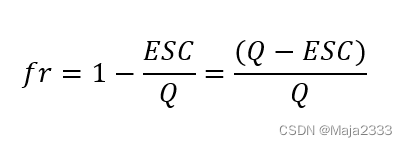
     只有当提前期内的需求超过再订货点时补货周期内才会发生缺货。设f(x)为提前期内需求分布的密度函数，则补货周期平均预期缺货量可用以下公式表示：


     当提前期的需求服从均值为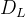![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)、标准差为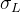![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)的正态分布时，假设安全库存为ss，上式可简化为：


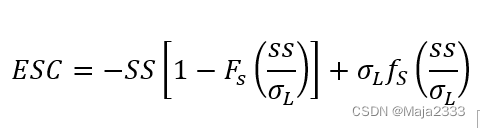
     可计算ESC如下：

计算给定期望满足率下所需的安全库存

    第一步是计算fr。


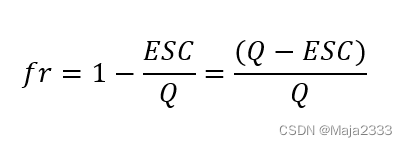
     第二步是计算安全库存。

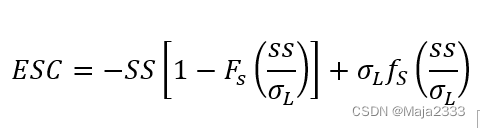
4.期望的产品可获性水平、提前期、需求的不确定性对安全库存的影响

    (1)**缩短供应商的提前期L**：如果提前期缩短为原来的1/k，则所需安全库存将减少为原来的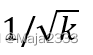![](https://img-blog.csdnimg.cn/c5d6da8168544493aa8e2fb15a9f76d4.png)。

    (2)**降低需求的潜在不确定性(用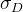![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)表示)**：如果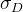![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)下降为原来的1/k，则所需的安全库存也将下降为原来的1/k。

5.根据块状化和季节性需求调整安全库存

    在实践中，制造商和分销商不是一次仅订购一件产品，而是大批量订货。因此，供应链各环节所观察到的需求往往是块状的。块状化增加了需求的波动。在实践中，可以通过将前面讨论的模型所建议的安全库存提高到顾客平均订货批量的一般来解决块状化问题。

四、供给不确定性对安全库存的影响

    假设每个时期的需求、供应商的补货提前期都服从正态分布。我们已知以下条件：

D=每个时期的平均需求

\sigma _{D}=每个时期需求的标准差

L=平均补货提前期

s_{L}=提前期的标准差

    已知提前期和每期的需求都是不确定的，提前期内需求服从均值为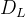![D_{L}](https://latex.csdn.net/eq?D_%7BL%7D)、标准差为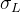![\sigma _{L}](https://latex.csdn.net/eq?%5Csigma%20_%7BL%7D)的正态分布，可得：


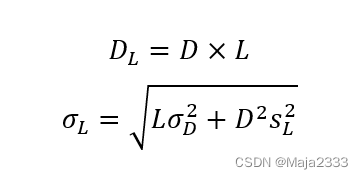
    已知提前期内需求的分布和期望CSL，可利用下式求出安全库存。

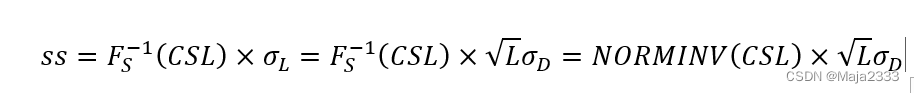
五、集中策略对安全库存的影响

    **集中**是供应链减少所需安全库存的最重要方法之一。在实践中，供应链有着不同程度的库存集中水平。

    假设有k个地区，每个地区的需求都服从正态分布。已知变量如下：

D_{i}=地区i的每期平均需求，i=1,2,...,k

\sigma _{i}=地区i每期需求的标准差，i=1,2,...,k

\rho _{ij}=地区i与地区j每期需求的相关性，i≤i≠j≤k

    有两种方法可用来满足k个地区的需求。一种方法是在每个地区设立本地库存，另一种方法是将所有库存都集中放在一个中心仓库。目标是对比这两种情况下的安全库存。设补货提前期为L，期望周期服务水平为CSL，利用

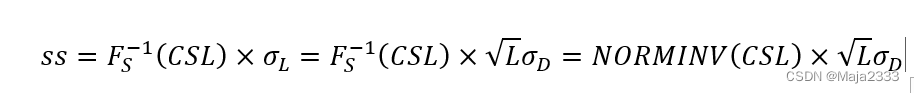
可得出：

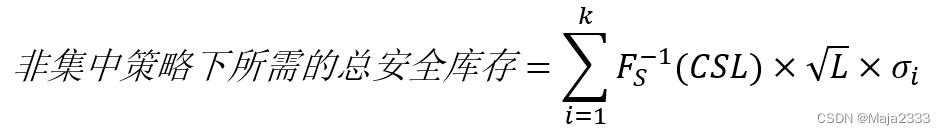
     如果全部库存都集中在一个中心仓库，首先需要估算集中后需求的分布情况，集中后的需求服从正态分布，其均值![D^{C}](https://latex.csdn.net/eq?D%5E%7BC%7D)、标准差为![\sigma _{D}^{C}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D%5E%7BC%7D)和方差![var(D^{C})](https://latex.csdn.net/eq?var%28D%5E%7BC%7D%29)分别为：


    上式是k个区域需求的集中，如果全部k个地区的需求分布相同，均值为D，标准差为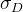![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)，且相关系数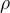![\rho](https://latex.csdn.net/eq?%5Crho)相同，则上式可简化为：


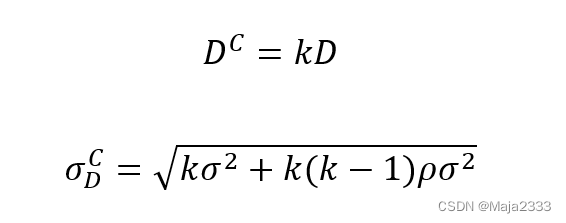
    如果所有k个区域的需求相互独立(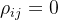![\rho _{ij}=0](https://latex.csdn.net/eq?%5Crho%20_%7Bij%7D%3D0))且分布相同，分布的均值为D，标准差为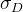![\sigma _{D}](https://latex.csdn.net/eq?%5Csigma%20_%7BD%7D)。则上式简化为：


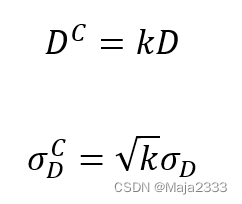
     根据下面两个公式：


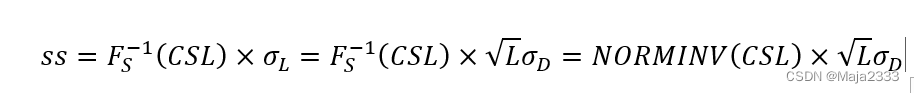
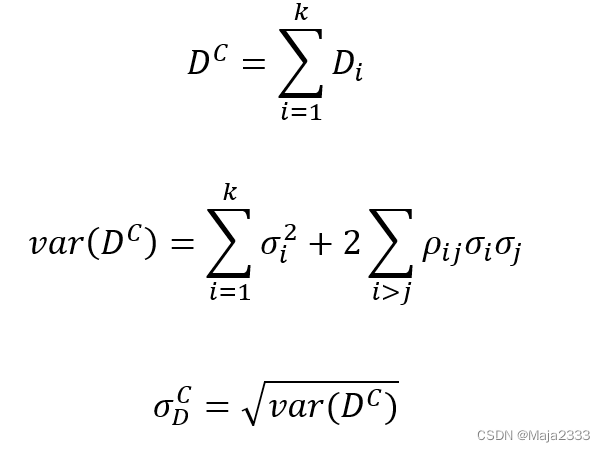
     可得：


     集中策略带来的单位销售量的库存持有成本的节约，可以通过将库存持有成本的节约额初一总需求kD得出。如果用H表示单位库存持有成本，根据下面两个公式：


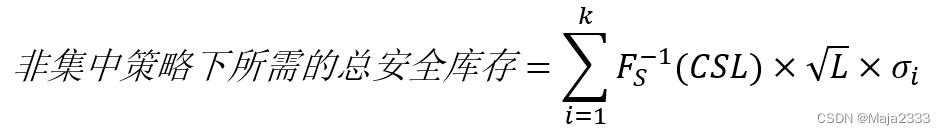
    可得单位销售量的库存持有成本节约为：


     ![(\sum_{i=1}^{k}\sigma _{i}-\sigma _{D}^{C})](https://latex.csdn.net/eq?%28%5Csum_%7Bi%3D1%7D%5E%7Bk%7D%5Csigma%20_%7Bi%7D-%5Csigma%20_%7BD%7D%5E%7BC%7D%29)的差值收相关系数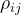![\rho _{ij}](https://latex.csdn.net/eq?%5Crho%20_%7Bij%7D)的影响。当相关系数接近-1时，这种差异很大；大相关系数接近1时，这种差异会缩小。只要相关系数小于1，集中策略就可以带来库存的节约。因此，由上式可得出有关**集中策略价值的结论**：

    -集中策略带来的安全库存随期望周期服务水平CSL的提高而增加；

    -集中策略带来的安全库存节约随提前期L的延长而增加

    -集中策略带来的安全库存节约随单位库存持有成本H的增加而增加

    -集中策略带来的安全库存节约随需求变异系数![(\sigma _{D}/D)](https://latex.csdn.net/eq?%28%5Csigma%20_%7BD%7D/D%29)的增加而增加

    -集中策略带来的安全库存节约随相关系数的增加而减少

    如果独立的库存地点数量减少为原来的1/n，则所需平均安全库存就将减少为原来安全库存的![1/\sqrt{}n](https://latex.csdn.net/eq?1/%5Csqrt%7B%7Dn)，这就是**平方根法则**。

    然而在某些情况下，将库存集中到一个地方并不是一个最优选择。将所有库存集中到一个地方可能带来以下**两大缺点**：

    (1)延长对顾客订单的响应时间

    (2)增加了将产品运送到顾客的运输成本

1.信息集中

    信息集中在确保高水平产品可获性的同时减少了安全库存

2.专业化

    集中带来的安全库存的减少在很大程度上取决于需求的变异系数

3.产品替代

    替代(substitution)是指利用一种产品去满足顾客对另一种不同产品的需求。这部分内容不详细介绍，感兴趣的读者自行上网查阅

4.零部件通用化

    这部分内容不详细介绍，感兴趣的读者自行上网查阅

5.延迟

    **延迟(postponement)**是指供应链将产品差异化或定制化推迟至接近产品销售时点的能力。这部分内容不详细介绍，感兴趣的读者自行上网查阅

六、补货策略对安全库存的影响

1.连续盘点策略

    给定期望CSL，目标是确定安全库存和再订货点。假设需求服从正态分布，并已知：

D=每个时期的平均需求

\sigma _{D}=每个时期需求的标准差

L=平均补货提前期

    再订货点表示提前期L内用于满足需求的现有库存。若提前期内的需求超过再订货点，则会出现缺货。如果各个时期的需求相互独立，提前期的需求服从如下正态分布：


     给定期望CSL，可分别球的安全库存和再订货点：


     管理者采用连续盘点策略只需要考虑提前期内的需求不确定性。因为对库存的连续监控使管理者能够根据需求情况调整下达补货订单的时点。

2.周期盘点策略

    在周期盘点策略中，每隔一段固定的时间间隔T盘点一次库存，并随即进行一次补货，使现有库存加上补货批量达到一个预先设定的水平，即目标最大库存水平(OUL)。盘点间隔期(review interval)也就是连续两次订货的时间间隔T。

    假设需求服从正态分布且各时期需求相互独立。假设已知以下参数：

D=每个时期的平均需求

\sigma _{D}=每个时期需求的标准差

L=平均补货提前期

T=盘点间隔期

CSL=期望周期服务水平

    必须确定一个目标最大库存水平以使下式成立：


     接着，求T+L时期的需求分布，T+L期间的需求服从正态分布，且


     目标最大库存水平和安全库存有如下关系：


     给定期望CSL，所需的安全库存计算如下：


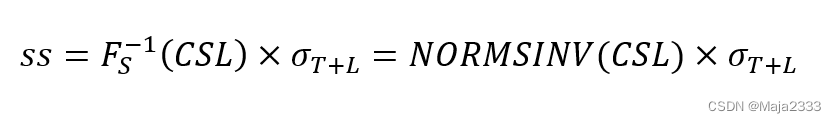
     平均批量等于盘点间隔期T内的平均需求，即

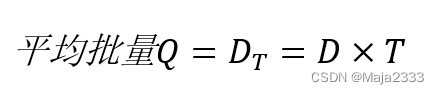
3.比较上面两种策略

    在连续盘点策略下，安全库存用于应对提前期L内的需求不确定性。在周期盘点策略下，安全库存应用于应对提前期和盘点间隔期L+T内的需求不确定性。由于周期盘点策略下必须面对更高的需求不确定性，因此周期盘点策略下要求的安全库存水平更高。

七、多级供应链中安全库存的管理

    多级供应链所有环节的安全库存水平是相互关联的。供应链某一环节至最终顾客质检的所有库存称为梯级库存(echelon inventory)。这就意味着如何在各个环节之间分配库存非常重要。这部分内容不详细介绍，感兴趣的读者自行上网查阅。

八、减少安全库存的管理杠杆

    降低供给不确定性是减少安全库存的一种重要管理杠杆。

    另一种有助于减少安全库存的管理杠杆是缩短提前期。

    减少安全库存的最后一种管理杠杆是降低供应链的需求不确定性。

补充：滞销商品的安全库存计算

目标：

** **设计一个需求近似泊松分布的滞销商品的安全库存的计算步骤。

分析：

    对于滞销商品，需求的分布更好使用需求到达率为D的泊松分布。在这种情况下，(Q,r)策略被认为是最优的。在(Q,r)策略下，只要把库存下降到或低于再订货点r，就发出订货，订货批量为nQ。其中n是指为了把库存水平提高到(r,r+Q)之内，所需的批量Q的倍数。

    对于泊松分布，假定提前期为固定值L，则提前期内的平均需求为LD,方差为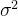![\sigma ^{2}](https://latex.csdn.net/eq?%5Csigma%20%5E%7B2%7D)=LD。费德格鲁恩提出了求解Q和r的有效算法。这这里给出的是基于加莱戈提出的启发式算法得出的。

    如果单位时间的单位库存持有成本为H，单位时间的单位固定缺货损失成本为p，S为每次订货的固定订货成本。加莱戈建议订货批量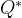![Q^{*}](https://latex.csdn.net/eq?Q%5E%7B*%7D)为：


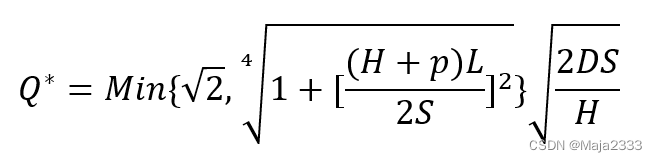
     加莱戈证明，使用批量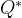![Q^{*}](https://latex.csdn.net/eq?Q%5E%7B*%7D)进行订货产生的成本与最优订货批量相比最多仅高出7%。再订货点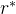![r^{*}](https://latex.csdn.net/eq?r%5E%7B*%7D)可利用费德格鲁恩和郑提出的方法球的。当需求服从泊松分布时，(r,Q)策略下的长期平均成本C(r,Q)为：

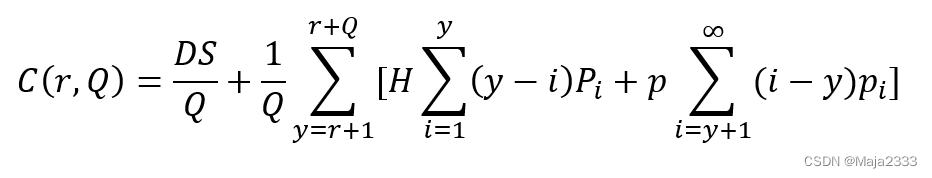
其中

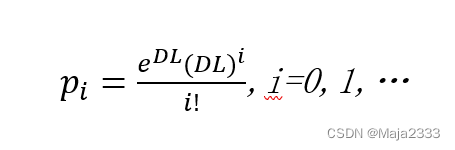
     订货点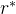![r^{*}](https://latex.csdn.net/eq?r%5E%7B*%7D)是通过由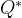![Q^{*}](https://latex.csdn.net/eq?Q%5E%7B*%7D)带入上式，然后寻找成本C(r,Q*)最小化的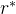![r^{*}](https://latex.csdn.net/eq?r%5E%7B*%7D)值得到的。由于C(r,Q*)是单峰的，r*可以用整数二分法查找求得。
标签： 交通物流 算法 数据挖掘
本文转载自: https://blog.csdn.net/weixin_56917624/article/details/131585778
版权归原作者 Maja2333 所有， 如有侵权，请联系我们删除。
登录后发布评论

“第四部分 供应链库存的计划和管理(二)供应链的不确定性管理:安全库存”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

机器人技术在安全领域的重要作用

安全学习记录——网络篇（一）

图腾柱PFC：HP1010为您的电动两轮车之旅提供绿色，高效，安全的动力

单元测试数据库回滚问题

这才是单元测试，之前我们都错了

【C语言基础】：字符函数和字符串函数

ChatGPT-Next-Web SSRF漏洞+XSS漏洞复现(CVE-2023-49785)

文章导航