人工智能导论：决策树算法求解分类预测问题

随便说点什么

最近好多好多的DDL啊啊啊…然后就搜索代码，结果在CSDN上面就怎么搜都搜不到…
于是我就发了…
应该现在搜这个的小伙伴应该都快要到考试周了吧，赶紧把实训做完，然后去好好复习吧！加油啊，祝你们考一个好成绩嗷！

距离考研的时间也就一年了，说实话其实多少还是很害怕的，再加上我自身的一些问题，现在处于一个迷失的状态已经好久好久了，对于一些事情想改变却好像根本无能为力，就挺迷茫的吧…
等考试周过去了，好好利用这个寒假调整好状态，然后冲鸭！

与诸君共勉【HUG】

注意：本博客仅供参考！！！

任务描述

本关任务：学习决策树，并基于离散的输入值和输出值数据归纳实现样例的布尔分类。

现有一些是否决定在该饭店等待餐桌吃饭的数据(x,y)，其中x是输入属性的值向量，y是单一布尔输出值，学员需要分析数据，构造一棵决策树，学习目标谓词 WillWait 的预测（ Yes 或者 No ），每一条数据属性如下：

Alternate ：附件是否有一个更合适的候选饭店（Yes 和 No）；

Bar ：饭店中是否有舒适的酒吧等待区（Yes 和 No）；

Fri/Sat ：当今天是星期五或星期六时，该属性为真 Yes ，否则为假 No；

Hungry ：是否饿了（Yes 和 No）；

Patrons ：饭店中有多少客人，取值为 None 、 Some 和 Full；

Price ：饭店价格区间；

Raining ：是否下雨（Yes 和 No）；

Reservation ：是否预定（Yes 和 No）；

Type ：饭店类型（French 、 Italian 、 Thai 和 Burger）；

WaitEstimate ：对等待时间的估计（0-10 、 10-30 、 30-60 和 >60 分钟）。

相关知识

为了完成本关任务，你需要掌握：1.决策树，2. ID3 算法，3.求解思路。

决策树

决策树表示一个函数，以属性值向量作为输入，返回一个“决策”，对于输入值是离散的和输出值是二值的情况，通常将这称之为布尔分类，其中样例输入被分类为正例（真）或反例（假），决策树在过程中则是通过一系列的计算测试达到决策的目的。

决策树学习的搜索策略是贪婪搜索策略，近似于极小化搜索树的深度，主要思想就是挑选分叉的属性，以便于尽可能对样例进行正确分类。一个完美属性可以将样例全部划分为正例集合和反例集合，这些集合对应决策树的叶子结点，哪些属性优先被选择就是决策树算法的核心，常见的选择算法有 ID3 算法和 C4.5 算法，本关卡重点介绍和学习 ID3 算法。

ID3算法

ID3（Iterative Dichotomiser 3 迭代二叉树三代） 算法是由 Ross Quinlan 发明的，它建立在奥卡姆剃刀理论的基础上，即越是小型的决策树越是优于大型的决策树，实际上也是一个启发式算法，是一种自顶向下增长树的贪婪算法，在每个结点选取能最好地分类样例的属性，重复这个过程，直到这棵树能完美分类训练样本或所有的属性都使用过了，其算法伪代码如下：

奥卡姆剃刀理论阐述了一个信息熵的概念，以此来选择最优分类属性。

举个例子来理解信息熵的定义，随机抛掷一枚硬币，出现正面和反面的概率都为0.5，根据以上熵的定义，可以得出以下式子：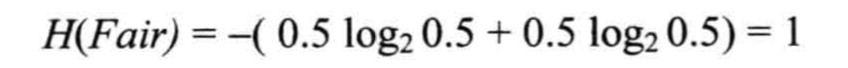

借助这个例子，设布尔随机变量以q的概率为真，则可定义该变量的熵为：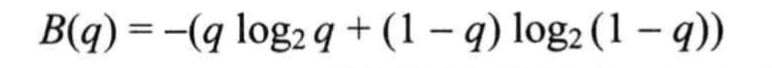

那么对于拥有多个属性的数据来说，ID3选择属性的方式则是计算该属性的信息增益（收益），信息增益最大的被优先选择作为决策树的分支属性。

对属性A的测试获得的信息增益为Gain(A)：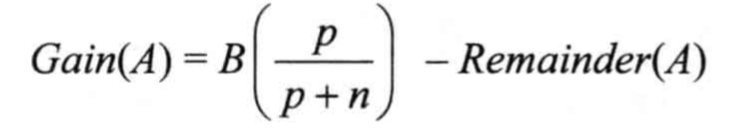

求解思路

样例学习的问题首先要做的就是好好的分析数据，详细了解代码 testDecisionTree.py 里的样例数据 data ，然后完成对数据的解析（计算出最优分类属性），并借助解析函数建立决策树，最终能完成对新输入案例的分类预测。

编程要求

本关的编程任务是补全右侧代码片段 build、predict、parse_data、calc_all_gain、calc_attr_gain、calc_bool_gain、get_targ 和 is_leaf 中 Begin 至 End 中间的代码，具体要求如下：

在build中，创建一棵决策树，输入参数为根结点；

在predict中，根据归纳好的决策树预测输入样例x的谓词 WillWait 状态（Yes 或者 No）；

在_parse_data_中，解析输入矩阵数据（在 Python 里以二维列表数据存储），各参数详见代码中函数注解，然后返回信息增益最大的属性名称及其属性值列表；

在_calc_all_gain_中，计算所有样本的信息熵并返回，各参数详见代码中函数注解；

在 calc_attr_gain 中，计算某一特征属性的信息熵并返回，各参数详见代码中函数注解；

在_calc_bool_gain_中，计算二值随机变量的信息熵并返回，各参数详见代码中函数注解；

在_get_targ_中，计算叶子结点的决策分类标签并返回，各参数详见代码中函数注解；

在_is_leaf_中，判断该结点是否为叶子结点，若是则返回 True，否则返回 False。

测试说明

平台将自动编译补全后的代码，并生成若干组测试数据，接着根据程序的输出判断程序是否正确。

以下是平台的测试样例：

测试输入：
[[example, Alt, Bar, Fri, Hun, Pat, Price, Rain, Res, Type, Est],[x1, Yes, No, No, Yes, Some, $$$, No, Yes, French, 0-10]]
预期输出：
Yes

代码

# -*- coding: UTF-8 -*-import math

classTreeNode:'''决策树结点数据结构
    成员变量：
    row - int 列表数据的行数，初始13
    col - int 列表数据的列数，初始12
    data - list[[]] 二维列表数据，初始数据形式在testDecisionTree.py里
                    第0行：[第0列：example(样本名字) 中间各列(1-10)：各个特征属性名称 第11列：WillW ait(目标分类) ]
                    第1-12行：[样本名字，具体属性值，分类目标]
        data = [
        ['example', 'Alt', 'Bar', 'Fri', 'Hun', 'Pat',  'Price', 'Rain', 'Res', 'Type',   'Est',   'WillW ait'],
        ['x1',      'Yes', 'No',  'No',  'Yes', 'Some', '$$$',   'No',   'Yes', 'French', '0-10',  'y1=Yes'   ],
        ['x2',      'Yes', 'No',  'No',  'Yes', 'Full', '$',     'No',   'No',  'Thai',   '30-60', 'y2=No'    ],
            ........            .....       .....       .........           ............
        ['x12',     'Yes', 'Yes', 'Yes', 'Yes', 'Full', '$',     'No',   'No',  'Burger', '30-60', 'y12=Yes'  ] ]
    targ - string 分类结果 Yes No
    name - string 结点名字：特征属性名称
    attr - list[string] 该特征属性下的各个属性值
    children - list[GameNode] 该特征属性下的各个决策树子结点，与 attr 一一对应
    '''def__init__(self, row, col, data):
        self.row = row
        self.col = col
        self.data = data
        self.targ =''# target result
        self.name =''# attribute name
        self.attr =[]# attribute value list
        self.child =[]# attribute - TreeNode ListclassDecisionTree:'''决策树
    成员变量：
    root - TreeNode 博弈树根结点
    成员函数：
    buildTree - 创建决策树
    predict - 预测样本分类标签
    _parse_data_ - 解析数据中最大信息增益的特性属性
    _calc_all_gain_ - 计算整个样本的信息熵
    _calc_attr_gain_ - 计算某一特征属性的信息熵
    _calc_bool_gain_ - 通用计算函数：计算二值随机变量的信息熵
    _get_targ_ - 获取叶子结点的决策分类标签
    _is_leaf_ - 判断该结点是否为叶子结点
    '''def__init__(self, row, col, data):
        self.root = TreeNode(row, col, data)defbuild(self, root):'''递归法创建博弈树
        参数：
        root - TreeNode 初始为决策树根结点
        '''

第一块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#if self._is_leaf_(root):
            root.targ = self._get_targ_(root)return
        root.name, root.attr = self._parse_data_(root.row, root.col, root.data)
        idj =[j for j inrange(root.col)if root.data[0][j]== root.name][0]for attr in root.attr:
            row =0
            col = root.col -1
            data =[]for i inrange(root.row):if i!=0and root.data[i][idj]!= attr:continue
                tmp =[]for j inrange(root.col):if j == idj:continue
                    tmp.append(root.data[i][j])
                data.append(tmp)
                row +=1
            node = TreeNode(row, col, data)
            root.child.append(node)for node in root.child:
            self.build(node)#********** End **********#

defpredict(self, root, x):'''分类预测
        参数：
        root - TreeNode 决策树根结点
        x - [[]] 测试数据，形如：
           [ ['example', 'Alt', 'Bar', 'Fri', 'Hun', 'Pat', 'Price', 'Rain', 'Res', 'Type',  'Est'],
             ['x1',      'Yes', 'No',  'No',  'Yes', 'Some', '$$$',  'No',   'Yes', 'French','0-10'] ]
        返回值：
        clf - string 分类标签 Yes No
        '''

第二块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#if self._is_leaf_(root):return root.targ
        id_name = x[0].index(root.name)for id_attr, attr inenumerate(root.attr):if attr == x[1][id_name]:return self.predict(root.child[id_attr], x)#********** End **********#

def_parse_data_(self, row, col, data):'''解析数据：计算数据中最大信息增益的特性属性
        参数：
        row - int 列表数据的行数
        col - int 列表数据的列数
        data - list[[]] 二维列表数据，形如：
                第0行：[第0列：example(样本名字) 中间各列(1-10)：各个特征属性名称 第11列：WillW ait(目标分类) ]
                第1-12行：[样本名字，具体属性值，分类目标]
        data = [
        ['example', 'Alt', 'Bar', 'Fri', 'Hun', 'Pat',  'Price', 'Rain', 'Res', 'Type',   'Est',   'WillW ait'],
        ['x1',      'Yes', 'No',  'No',  'Yes', 'Some', '$$$',   'No',   'Yes', 'French', '0-10',  'y1=Yes'   ],
        ['x2',      'Yes', 'No',  'No',  'Yes', 'Full', '$',     'No',   'No',  'Thai',   '30-60', 'y2=No'    ],
            ........            .....       .....       .........           ............
        ['x12',     'Yes', 'Yes', 'Yes', 'Yes', 'Full', '$',     'No',   'No',  'Burger', '30-60', 'y12=Yes'  ] ]
        返回值：
        clf - string, list[] 信息增益最大的属性名称 及其 属性值列表
        '''

第三块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#
        max_gain =-float('inf')
        max_name =''
        max_attr =[]
        max_idj =-1
        all_gain = self._calc_all_gain_(row-1,[x[-1]for x in data[1:]])# col = 1#print('all_gain: ', all_gain)for j inrange(1, col-1,1):
            tmp_data =[]for i inrange(1, row,1):
                tmp_data.append([data[i][j], data[i][-1]])
            tmp_gain = self._calc_attr_gain_(row-1, tmp_data)# col = 2if(all_gain - tmp_gain)> max_gain:
                max_gain = all_gain - tmp_gain
                max_name = data[0][j]
                max_idj = j
            #print(max_gain, max_name, max_idj, tmp_gain, data[0][j], all_gain - tmp_gain)for i inrange(1, row,1):if data[i][max_idj]notin max_attr:
                max_attr.append(data[i][max_idj])return max_name, max_attr
        #********** End **********#

def_calc_all_gain_(self, row, data):'''计算整个样本的信息熵
        参数：
        row - int 列表数据的行数
        data - list[] 一维列表数据，形如：[分类目标]
                data = ['y1=Yes', 'y2=No', ........, 'y12=Yes']
        返回值：
        clf - float 信息熵
        '''

第四块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#
        dict_ ={'yes':0.0,'no':0.0}for i inrange(row):if data[i][-1]=='s':# 'Yes'
                dict_['yes']+=1.0else:# 'No'
                dict_['no']+=1.0sum=0.0for key_ in dict_:sum+=(1.0* dict_[key_]/float(row))* math.log(1.0* dict_[key_]/float(row),2)return-sum#********** End **********#

def_calc_attr_gain_(self, row, data):'''计算某一特征属性的信息熵
        参数：
        row - int 列表数据的行数
        data - list[[]] 二维列表数据（2列），形如：[[某一属性值，分类目标]]
                  [ ['0-10',  'y1=Yes'   ],
                    ['30-60', 'y2=No'    ],
                      ........
                    ['30-60', 'y12=Yes'  ] ]
        返回值：
        clf - float 信息熵
        '''

第五块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#
        dict_ ={}for i inrange(row):if data[i][0]notin dict_:
                dict_[data[i][0]]=[0.0,0.0]# [yes, no]# attribute : yes or noif data[i][1][-1]=='s':# yes
                dict_[data[i][0]][0]+=1.0else:# no
                dict_[data[i][0]][1]+=1.0sum=0.0for key_ in dict_:
            p =1.0* dict_[key_][0]/(dict_[key_][0]+ dict_[key_][1])sum+=(1.0*(dict_[key_][0]+ dict_[key_][1])/float(row))* self._calc_bool_gain_(p)returnsum#********** End **********#

def_calc_bool_gain_(self, p):'''通用计算函数：计算二值随机变量的信息熵
        参数：
        p - float 二值随机变量的概率 在[0, 1]之间
        返回值：
        clf - float 信息熵
        '''

第六块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#if p ==1or p ==0:return0.0return-(p * math.log(p,2)+(1-p)* math.log((1-p),2))#********** End **********#

def_get_targ_(self, node):'''计算叶子结点的决策分类标签
        参数：
        node - TreeNode 决策树结点
        返回值：
        clf - string 分类标签 Yes No
        '''

第七块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#
        yes =0
        no =0for i inrange(1, node.row,1):if node.data[i][-1][-1]=='s':# 'Yes'
                yes +=1else:# 'No'
                no +=1if yes > no:return'Yes'else:return'No'#********** End **********#

def_is_leaf_(self, node):'''判断该结点是否为叶子结点
        参数：
        node - TreeNode 决策树结点
        返回值：
        clf - bool 叶子结点True 非叶子结点False
        '''

第八块待补充代码块：

#请在这里补充代码，完成本关任务#********** Begin **********#if node.col ==2:# [ x* , y* ] without any attributesreturnTrue
        targ = node.data[-1][-1][-1]# [ x* , attr , y* ] attributesfor i inrange(node.row):if i ==0:continueif node.data[i][-1][-1]!= targ:returnFalsereturnTrue#********** End **********#