机械转码日记【3】——《数据结构》堆的实现及堆的应用

前言：

看了看上一篇博客的时间，2021.12.15，实在是太不好意思啦，拖更了这么久，前段时间一直在忙导师的项目，但是也没有停止学习，最近正在学习数据结构，感觉堆的算法非常的妙啊！于是有感而发写了这篇博客。

堆的详细代码可以移步到我的gitee：比特李鑫/数据结构

堆是个啥？

堆在逻辑上是一棵特殊的完全二叉树，为什么特殊呢？因为堆中某个节点的值总是不大于或不小于其父节点的值，而通过根节点的大小，又可以将堆分为大堆和小堆，将根节点最大的堆叫做大堆，根节点最小的堆叫做小堆。而堆如何储存在内存中呢，一般是用数组储存的。如图所示：

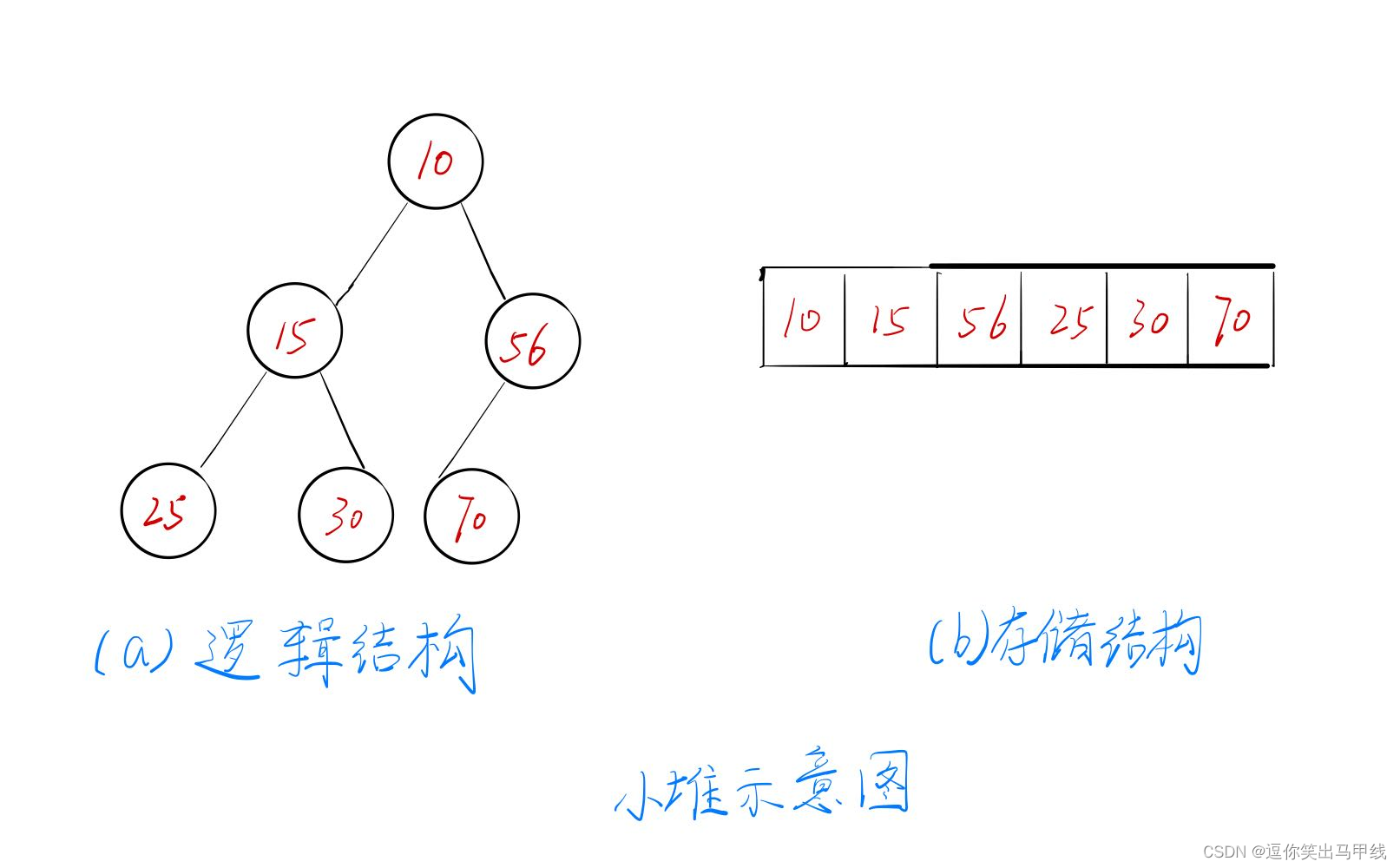
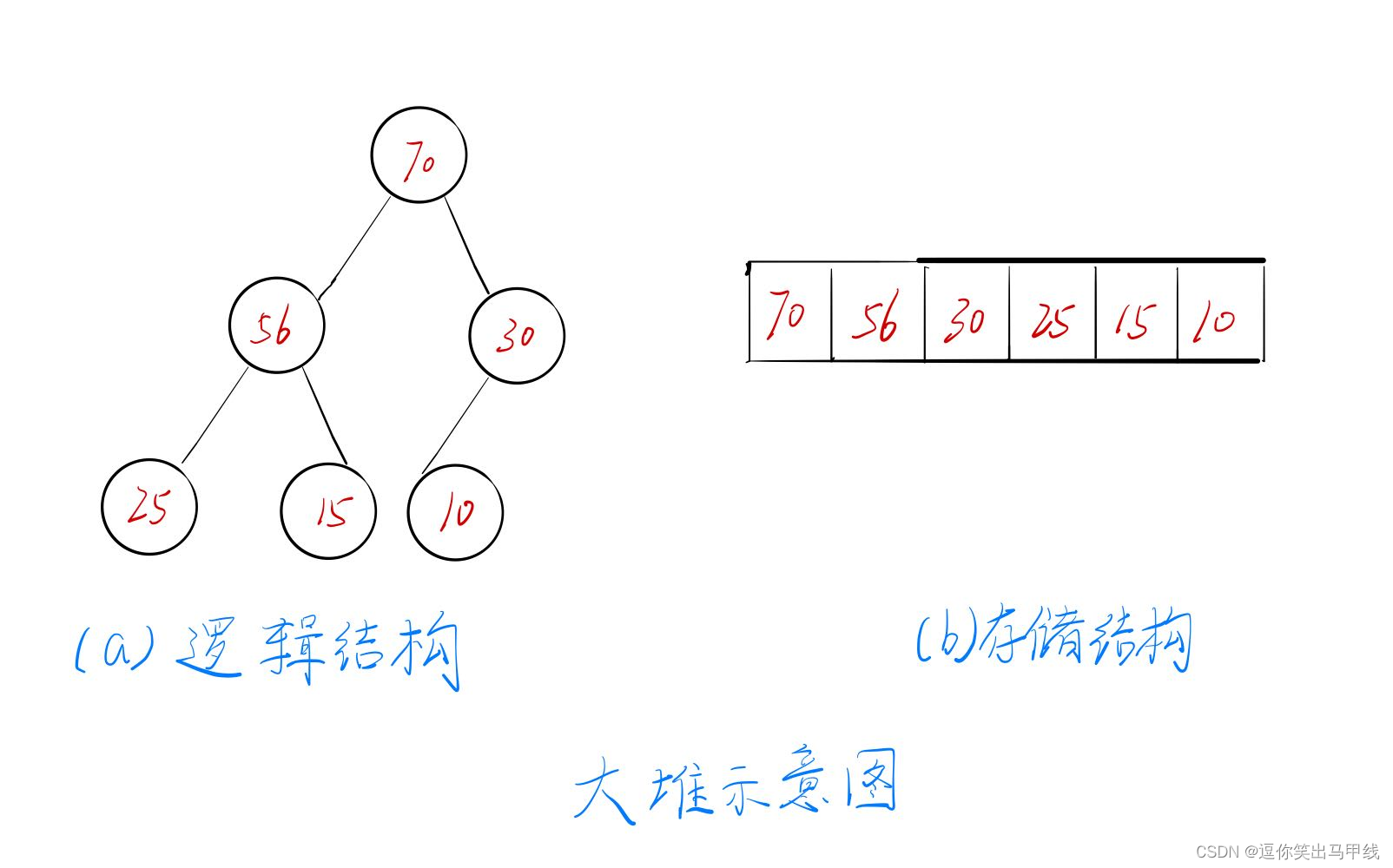
堆如何用代码实现？

先定义一个能够动态调整大小的数组

前面说过了，因为堆的存储结构是一个数组，那如果需要在堆上进行增删查改的操作，就必须定义一个能够动态调整大小的数组，代码如下：

typedef int HPDataType;
typedef struct Heap
{
    HPDataType* a;//存储堆数据的数组
    int size;//堆的数据个数
    int capacity;//数组的容量
}Heap;

堆的插入（向上调整算法）

假如我们要在一个堆中插入一个数据，并且在插入后不改变堆的性质（假如原先是大堆，那么插入了新的数据之后仍然是大堆），那么我们需要用到向上调整算法，例如我需要再下图的堆中插入一个新数据“10”。

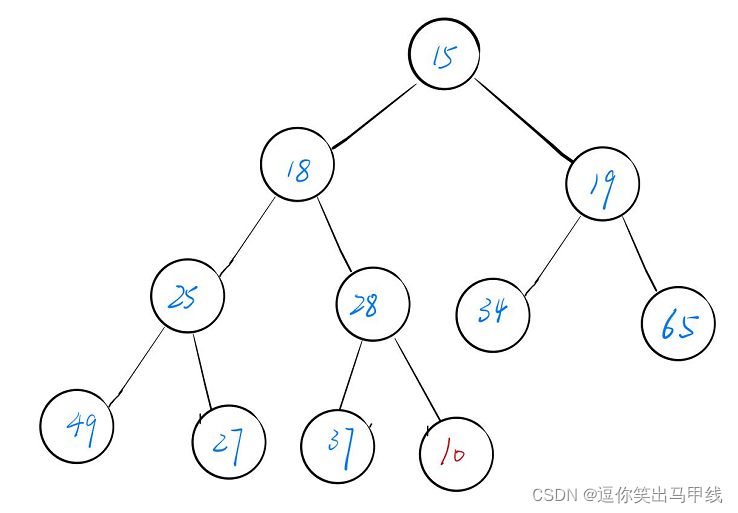
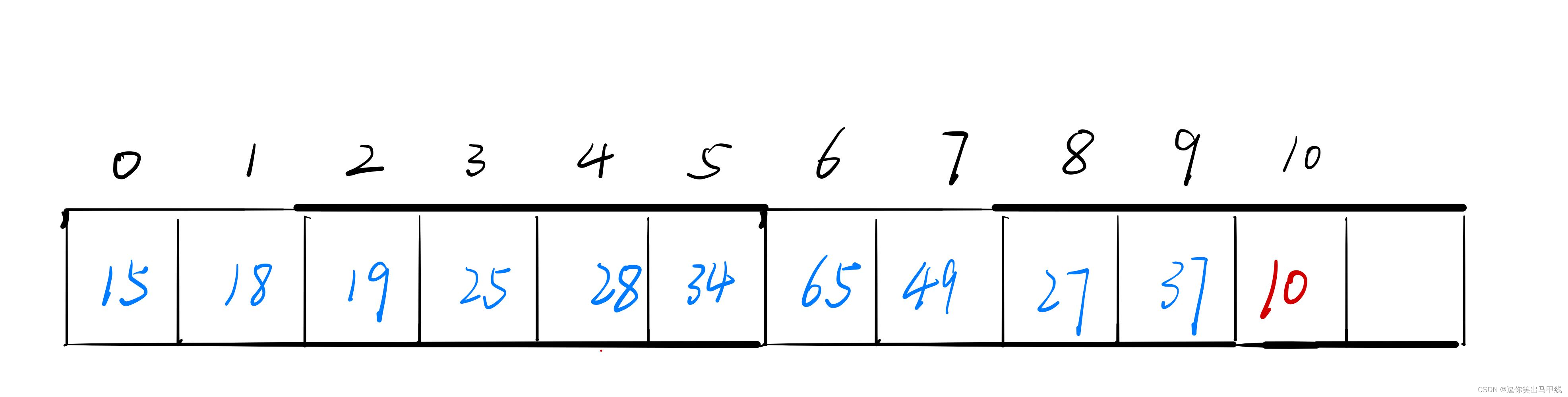假如我们不调整“10”在数组中的位置，那么它就不符合堆的性质，所以我们必须调整，那么如何调整呢：

1. 我们需要找到“10”的父亲节点，如何找到10的父亲的小标呢，我们可以使用公式:parent=(child-1)/2；
2. 比较父亲和子节点的大小关系，如果比他的父亲节点小，就不符合大堆的性质，此时我们交换10和父亲节点的值；
3. 这个时候仍然需要比较10现在与父亲节点的大小关系，那么我们就需要重复这个过程，直到满足堆的性质。

整个过程如下图所示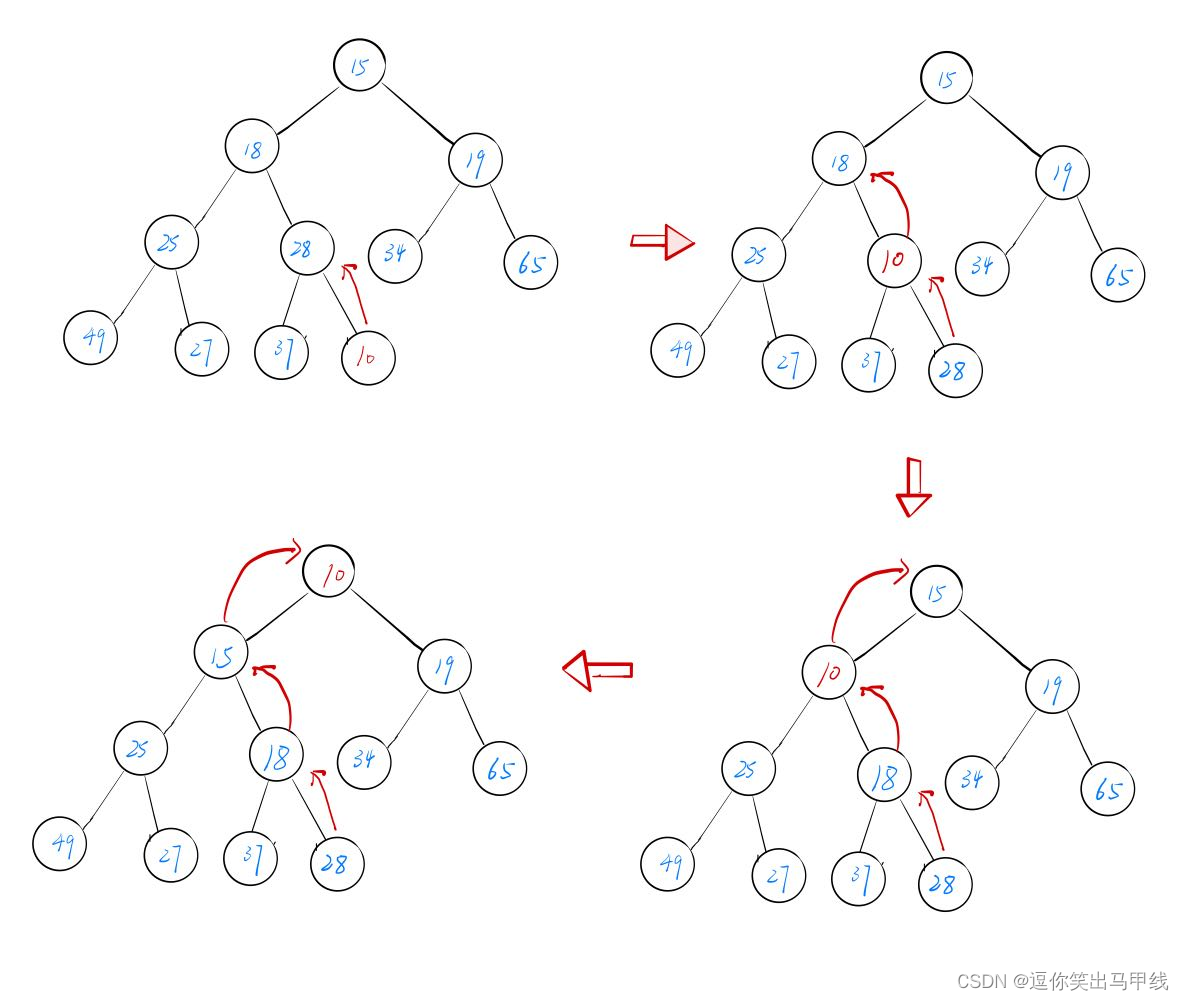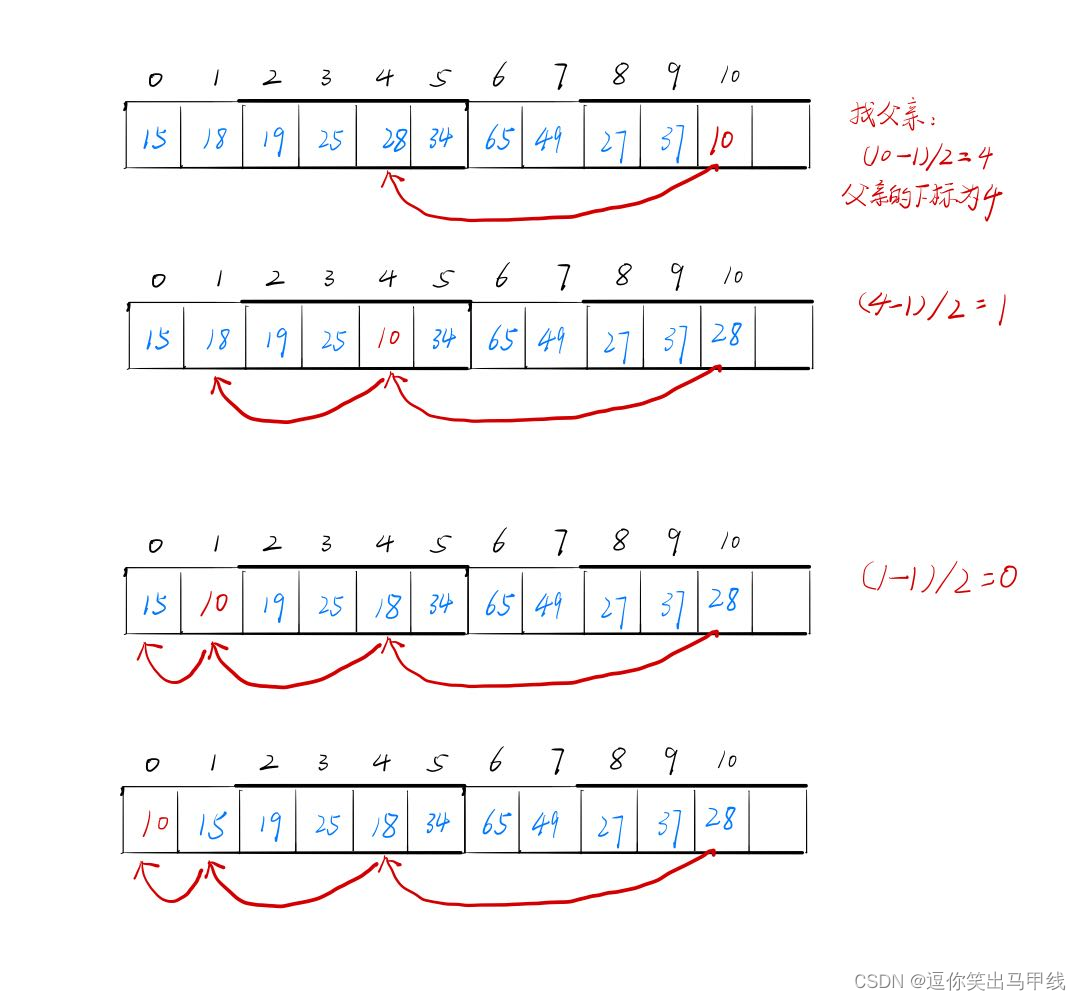： 代码实现如下：

//向上调整算法
//a为需要修改的堆的地址，child为向上调整时，孩子节点的下标
void AdjustUp(HPDataType* a, size_t child)
{
    assert(a);
    size_t parent = (child - 1) / 2;
    while (child > 0)
    {
        //大堆
        //if (a[child] > a[parent])
        //小堆
        if (a[child]<a[parent])
        {
            Swap(&a[child],&a[parent]);
            child = parent;
            parent = (parent - 1) / 2;
        }
        else
        {
            break;
        }
    }
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
    assert(hp);
    checkcapacity(hp);
    hp->a[hp->size] = x;
    AdjustUp(hp->a, hp->size);
    hp->size++;
}

堆的删除 （向下调整算法）

如果我们需要删除堆的根节点，并且在删除根节点后，我们的堆的性质保持不变（假如原先是小堆，那么删除根节点之后仍然是小堆），那么此时我们就要用到向下调整算法。具体如何做呢？

1. 交换根节点与最后一个节点的值
2. 删除最后一个节点（此时就相当于删除掉了根节点的值）
3. 找出现在的根节点的两个孩子节点中的较小值，并进行比较，如果父亲比孩子大，则交换数值
4. 重复第3步，直到满足堆的性质。

整个过程如下图所示：

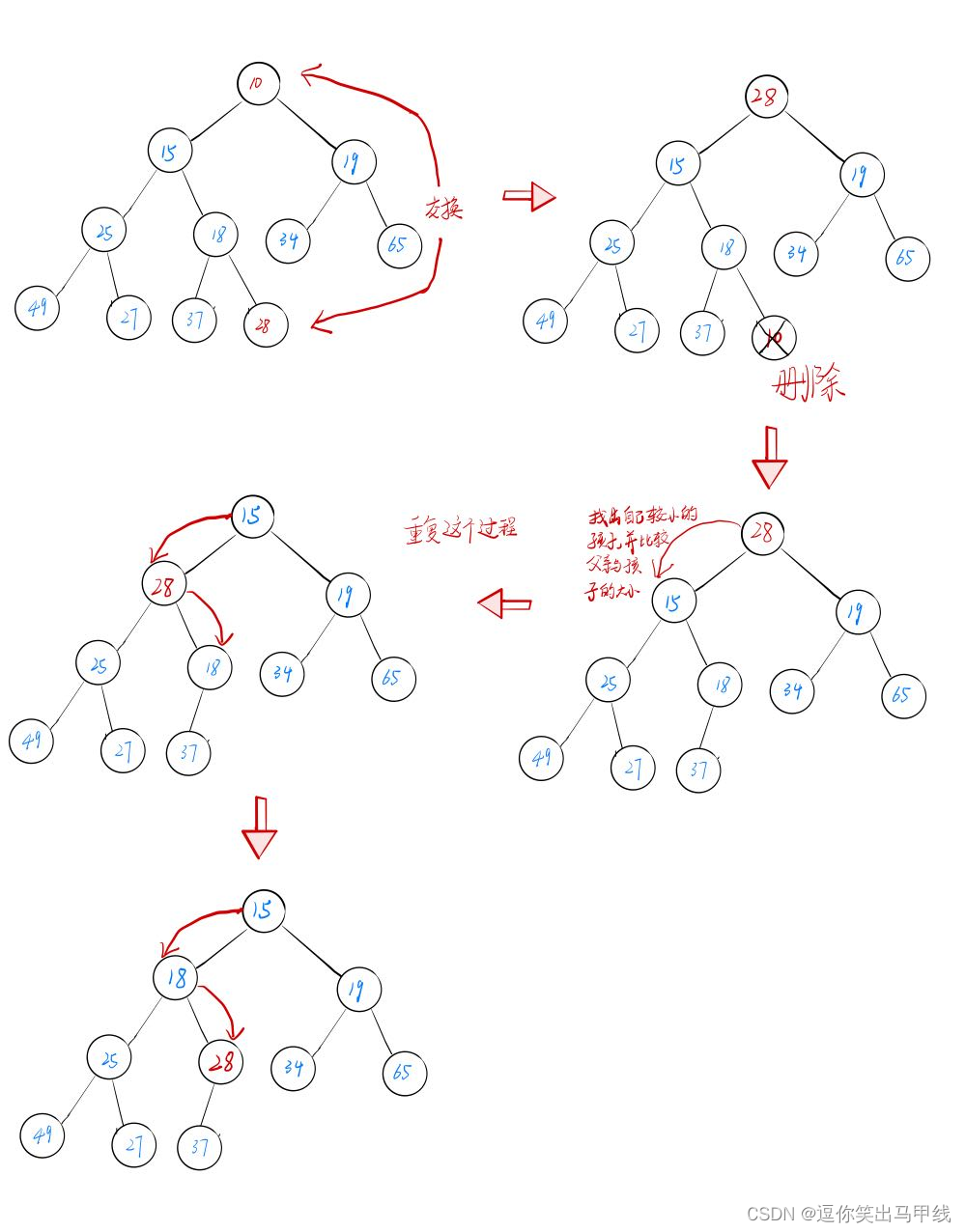
代码实现如下：

//向下调整算法
//a为需要修改的堆的地址，size为堆的有效数据个数，root为向下调整时根节点的下标
void AdjustDown(HPDataType* a, size_t size, size_t root)
{
    assert(a);
    size_t parent = root;
    size_t child = parent * 2 + 1;
    while (child<size)
    {
        //先找出那个较小的孩子
        //判断大小的同时要注意是否有右孩子节点，即是否造成数组越界
        if (child + 1 < size && a[child + 1] < a[child])
        {
            child++;
        }
        //小堆，如果爸爸比孩子大，就往下调整
        if (a[parent] > a[child])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}
// 堆的删除
void HeapPop(Heap* hp)
{
    assert(hp);
    assert(hp->size > 0);
    Swap(&(hp->a[(hp->size) - 1]), &(hp->a[0]));
    AdjustDown(hp->a, hp->size, 0);
    hp->size--;
}

堆的应用(Top-K问题)

堆的应用，生活中最常见的就是Top-K问题啦，比如王者荣耀里面的国服前十后羿，美团外卖里面的你所在附件地区排名前十的凉皮肉夹馍（夹带私货，我喜欢吃凉皮肉夹馍哈哈哈哈哈），这些都属于Top-K问题，而Top-K问题涉及了堆排序问题，那么我们如何使用代码去实现堆排序呢？

1. 在需要排序的数据中建堆，如果是升序，就建立大堆，如果是降序，就建立小堆
2. 利用堆删除思想去实现堆排序

在数组上建堆

如何在数组上建堆呢，有两种方法，第一种是使用向下调整算法建堆，第二种是使用向上调整算法建堆，我更推荐向下调整法建堆，因为向下调整法建堆的时间复杂度为O（N），向上调整法建堆的时间复杂度为O（N*LogN）。（至于如何计算他们的时间复杂度，代码的实现原理，以及为什么升序建立大堆，降序建立小堆；我会再写一篇博客进行说明，这次一定不会断更！）

利用堆删除思想去实现堆排序

前面说了，如果是升序，就建立大堆，下面我就以大堆为例，实现一组数据的升序排序。其基本步骤如下：

1. 交换根节点与最后一个节点（end）
2. end节点减1，即指向倒数第二个节点；
3. 将交换后的根节点向下调整，使新的完全二叉树仍然满足大堆的性质
4. 重复执行1.2.3步，直到end为0；

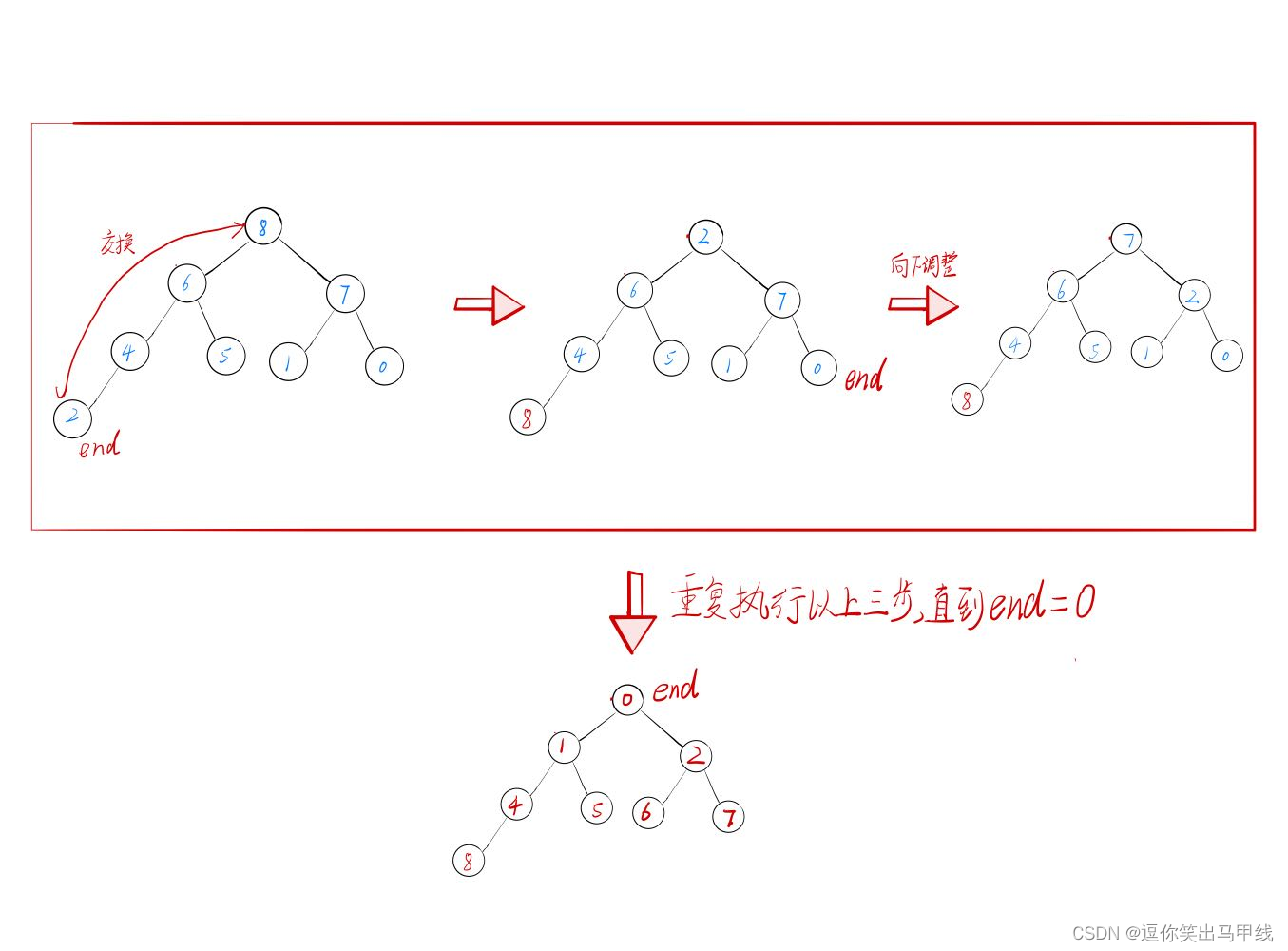
堆排序的代码实现如下

//在堆上排序
void HeapSort(int* a, int size)
{
    //向上调整建堆
    /*
    for (int i = 0; i < size; i++)
    {
        AdjustUp(a, i);
    }
    */
    //向下调整建堆
    for (int i = (size - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(a, size, i);
    }
    //通过堆删除原理实现排序
    int end = size - 1;
    while (end > 0)
    {
        swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        end--;
    }
}

Top-K问题的代码实现

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合的前k个数来建立堆，如果求最小的k个数就建立大堆，求最大的k个数就建立小堆
2. 将数据集合中的其余n-k个数与堆顶的数进行比较；如果是小堆，且这个数比堆顶数据大就替换堆顶数并向下调整；如果是大堆，且这个数比堆顶数据小就替换堆顶数并向下调整。

代码实现如下：

// 以找最大的前K个为例，建立K个数的小堆
void PrintTopK(int* a, int n, int k)
{
    // 1. 建堆--用a中前k个元素建堆
    int* kminHeap = (int*)malloc(sizeof(int) * k);
    assert(kminHeap);

    for (int i = 0; i < k; ++i)
    {
        kminHeap[i] = a[i];
    }

    // 建小堆
    for (int j = (k - 1 - 1) / 2; j >= 0; j--)
    {
        AdjustDown(kminHeap, k, j);
    }

    // 2. 将剩余n-k个元素依次与堆顶元素交换，大于堆顶元素则替换,并向下调整
    for (int i = k; i < n; i++)
    {
        if (a[i] > kminHeap[0])
        {
            kminHeap[0] = a[i];
            AdjustDown(kminHeap, k, 0);
        }
    }

    for (int j = 0; j < k; j++)
    {
        printf("%d ", kminHeap[j]);
    }
    printf("\n");
    free(kminHeap);
}