(HGNN) Hypergraph Neural Networks

Hypergraph Neural Networks

1.Abstract

提出了一个用于数据表示学习的超图神经网络（HGNN）框架，它可以在超图结构中编码高阶数据相关性。面对在实际实践中学习复杂数据表示的挑战，我们建议将这种数据结构合并到超图中，这在数据建模上更加灵活，特别是在处理复杂数据时。该方法设计了一种超边卷积操作来处理表示学习过程中的数据相关性。这样，传统的超图学习过程就可以有效地使用超边卷积运算来进行。HGNN能够学习考虑高阶数据结构的隐藏层表示，这是一个考虑复杂数据相关性的通用框架。我们进行了引文网络分类和视觉目标识别任务的实验，并将HGNN与图卷积网络等传统方法进行了比较。实验结果表明，所提出的HGNN方法优于最近的先进方法。我们还可以从结果中表明，所提出的HGNN在处理多模态数据时优于现有的方法。

2.Introduction

基于图的卷积神经网络（GCN）（Kipf和Welling 2017）、（德弗拉德、布列森和范德海斯特2016）近年来引起了人们的广泛关注。与传统的卷积神经网络不同，图卷积能够使用神经网络模型对不同输入数据的图结构进行编码，并可用于半监督学习过程。图卷积神经网络由于其使用数据图结构的能力，与传统神经网络相比，在表示学习方面的优势

在传统的图卷积神经网络方法中，采用了数据之间的成对连接。值得注意的是，实际实践中的数据结构可能超出成对连接，甚至复杂得多。面对多模态数据的情景，数据相关建模的情况可能更加复杂。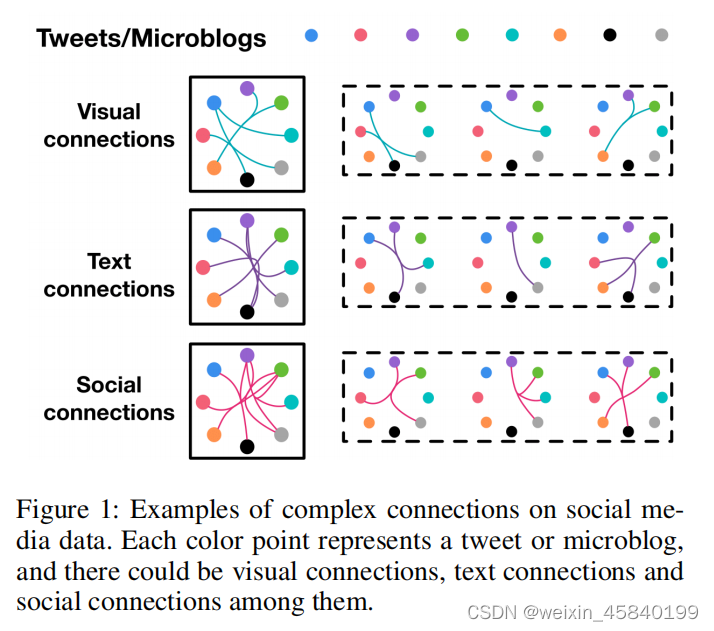

GCN局限：
一方面，数据相关性可能比成对关系更复杂，这很难用图结构来建模。另一方面，数据表示倾向于多模态的，如本例中的视觉连接、文本连接和社会连接。在这种情况下，传统的图结构在表示数据相关性方面存在局限性，这限制了图卷积神经网络的应用。在这种情况下，进一步研究更好、更通用的数据结构模型来学习表示是重要而迫切的。

改进：
在本文中，提出了一个超图神经网络（HGNN）框架，它使用超图结构进行数据建模。与简单图相比，所有边的度都是强制的2，超图可以使用其无度超边编码高阶数据相关性（超越成对连接），如图2所示。在图2中，该图使用邻接矩阵表示，其中每条边只连接两个顶点。相反，对于多模态和异构的，超图易于扩展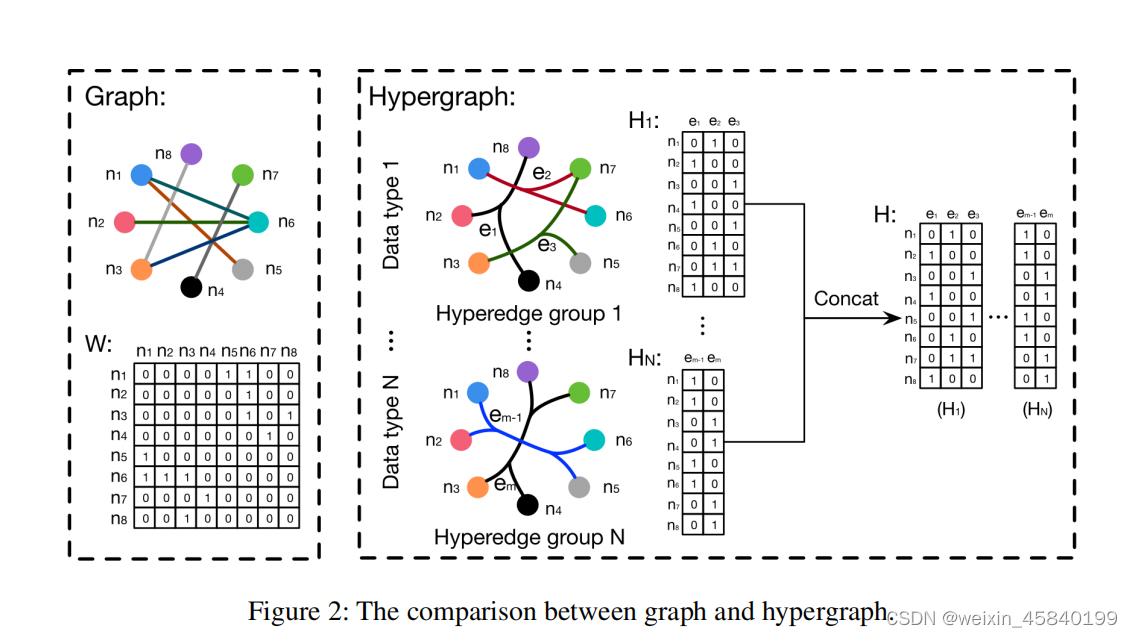

3.main contributions

1.提出了一个超图神经网络框架，即HGNN，用于使用超图结构的表示学习。HGNN能够通过其超图结构来表示复杂的高阶数据相关性，也可以有效地使用超边卷积操作。它对处理多模态数据/特征是有效的。此外，GCN（Kipf和Welling 2017）可以被视为HGNN的一种特殊情况，其中简单图中的边可以看作是仅连接两个顶点的二阶超边。

2.我们对引文网络分类和视觉对象分类任务进行了广泛的实验。与最先进的方法的比较证明了所提出的HGNN框架的有效性。实验结果也表明，该方法在处理多模态数据时具有较好的性能。

4.Hypergraph Neural Networks（HGNN）

1.Hypergraph learning statement

与简单图不同，超图中的超边连接两个或多个顶点。一个超图被定义为G =（V，E，W），它包括一个顶点集V，一个超边缘集E。每个超边都用W分配一个权值，一个边权值的对角矩阵。超图G可以用|V|×|E|关联矩阵H表示，条目定义为

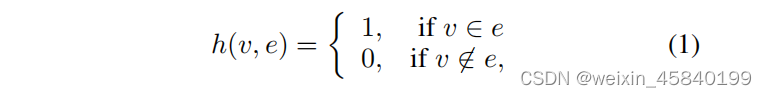
对于一个顶点v∈V，它的度被定义为d(v)=Pe∈Eω(e)h（v，e）。对于一个边的e∈e，它的度被定义为δ(e)=Pv∈Vh（v，∈）。此外，De和Dv分别表示边度和顶点度的对角矩阵。

这里让我们考虑超图上的节点（顶点）分类问题，其中的节点标签在超图结构上应该是平滑的。该任务可以表述为由（Zhou，Huang，和Sch¨olkopf2007）介绍的正规化框架：

其中Ω(f)是超图上的正则化，Remp (f)表示监督经验损失，f（·）是一个分类函数。其中∆是正半定的，通常称为超图拉普拉斯行列式。

2.Spectral convolution on hypergraph

给定一个超图G =（V，E，∆）n顶点，因为超图拉普拉斯∆是n×正半定矩阵，特征分解∆= ΦΛΦ>可以用来得到标准正交特征向量Φ=数据（φ1，…，φn）和对角矩阵Λ=图（λ1，…，λn）包含相应的非负本征值。将超图中信号x =（x1，…，xn）的傅里叶变换定义为ˆx=Φ>x，其中特征向量视为傅里叶基，特征值解释为频率。信号x和滤波器g的频谱卷积可以记为：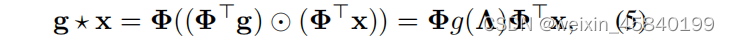

3. Hypergraph neural networks analysis

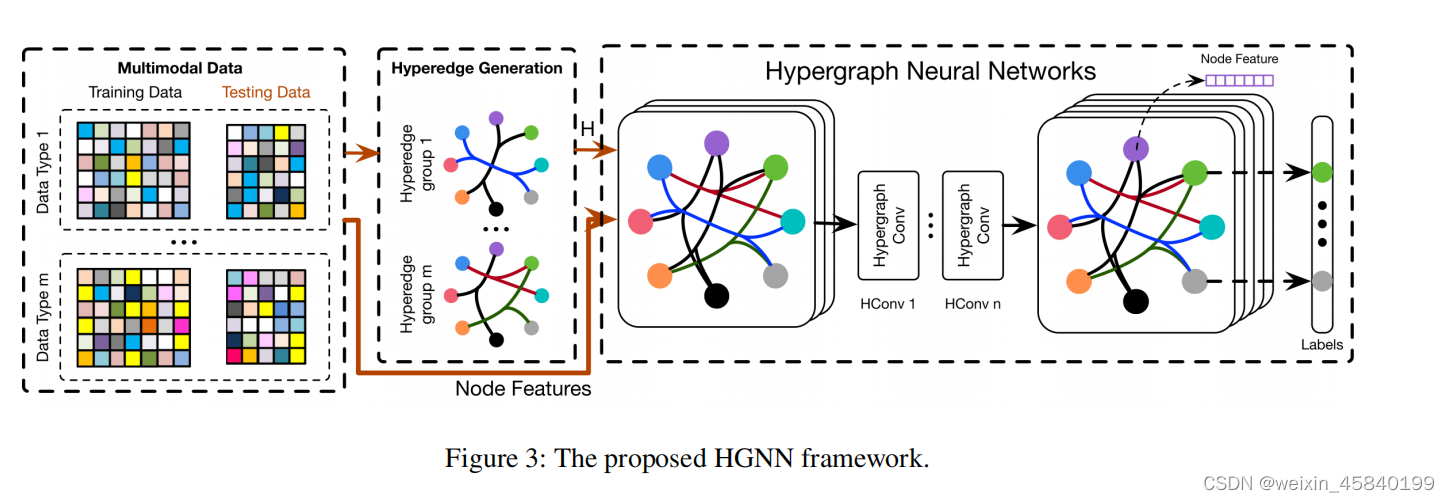
将多模态数据集分为训练数据和测试数据，每个数据包含几个具有特征的节点。然后利用多模态数据集的复杂相关性构造了多个超边缘结构群。我们将超边群连接起来，生成超图相邻矩阵H，将超图相邻矩阵H和节点特征输入HGNN，得到节点输出标签。如上一节所述，我们可以用下面的公式建立一个超边卷积层f（X，W，Θ）

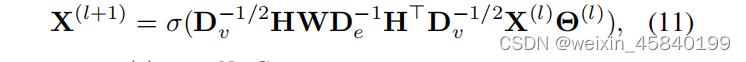
其中，X (1)∈RN×C为l层超图的信号，X (0) = X和σ为非线性激活函数。

HGNN模型是基于超图上的谱卷积。在这里，我们进一步研究了HGNN在数据间利用高阶相关性的特性。如图4所示，HGNN层可以进行节点边-节点变换，这可以利用超图结构更好地细化特征。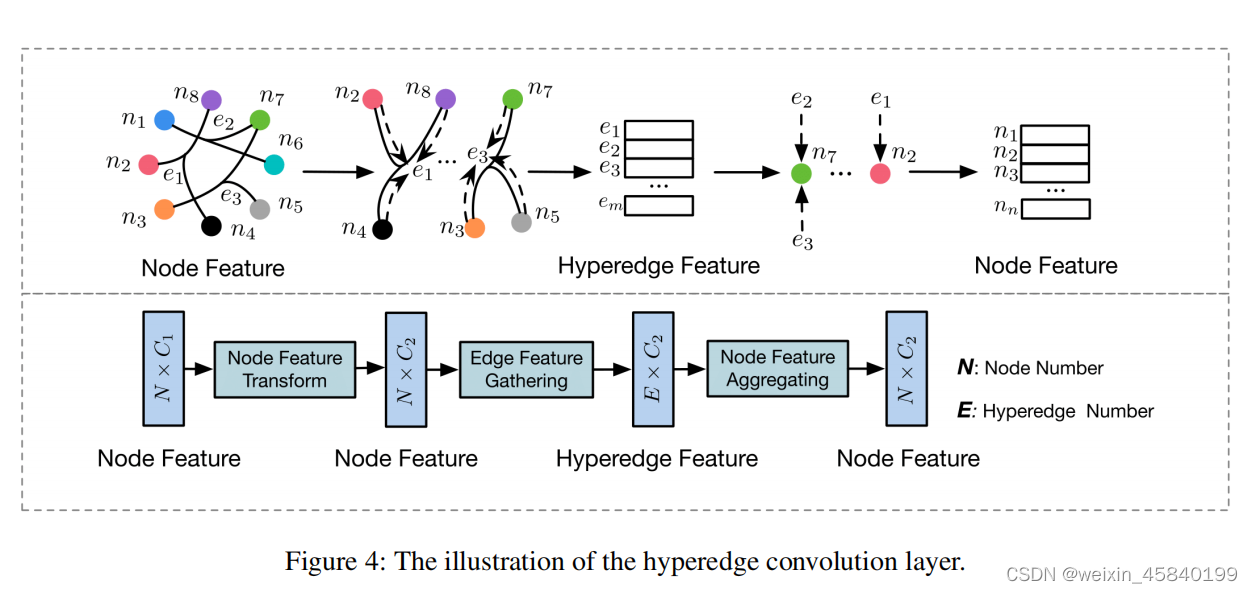

4. Relations to existing methods

当超边只连接两个顶点时，超图被简化为一个简单图，拉普拉斯∆也与简单图的拉普拉斯∆一致，最高可达12倍。与现有的图卷积方法相比，我们的HGNN可以自然地建模数据之间的高阶关系，在形成特征提取中得到了有效的利用和编码。与传统的超图方法相比，我们的模型在不需要拉普拉斯∆逆运算的情况下具有高的计算效率。值得注意的是，我们的HGNN对多模态特性具有很大的可扩展性，并具有超边缘生成的灵活性。

5.Experiments

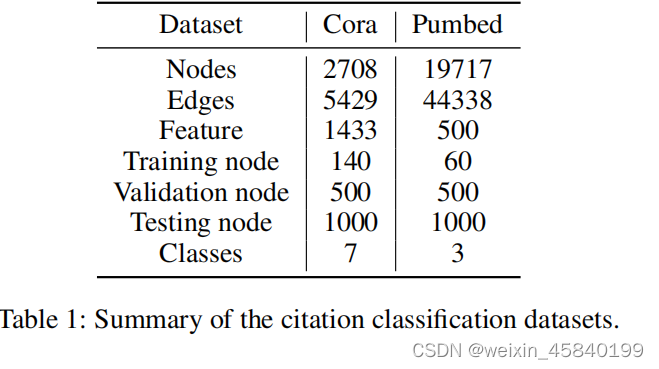
6.Conclusion

在本文中，提出了一个超图神经网络（HGNN）的框架。在该方法中，HGNN将卷积运算推广到超图学习过程中。利用超图拉普拉斯对谱域进行卷积，并用截断的切比雪夫多项式进一步逼近。HGNN是一个更一般的框架，与传统的图相比，它能够通过超图结构来处理复杂的高阶相关性来进行表示学习。我们进行了引文网络分类和视觉目标识别任务的实验，以评估所提出的HGNN方法的性能。实验结果和与最先进的方法的比较表明，所提出的HGNN模型具有更好的性能。HGNN能够将复杂的数据相关性应用到表示学习中，从而在许多任务中导致潜在的广泛应用，如视觉识别、检索和数据分类。