嘿，算法，哪里跑｜你知道“时间复杂度”吗｜算法初识

14天阅读挑战赛

为了小杯子，一直在努力！

算法

这里我感觉《趣学算法》陈小玉教授 给的建议真的很不错。

一、学习建议

1. 多角度，对比学习①入门书籍，由简向复学习 ②多本算法，对比学习
2. 大视野，不求甚解****①优先级 算法思路，解题思路＞弄懂算法实现 (不会因为某个公式/几行代码而“抛锚”停止不前)
3. 多交流，见贤思齐“同学”，“教师”，“论坛”，“交流群”，“讲座”，“技术性活动”等
4. 勤实践，越挫越勇不要一味的学习理论知识，“实践才是检验真理的唯一标准”，不惧怕失败，在错误中成长。
5. 看电影，洞察未来“科幻电影” 增长见识，有部分科幻电影中的情节，已经与我们见面了。

数据结构 +算法＝程序

这句话我相信很多人都有所耳闻。包括我的老师也经常给我们灌输这一概念

二、探讨算法

1. 算法具有以下特征① 有穷性（不会出现无限循环，每个步骤在一个可以接受的时间内完成） ② 确定性（算法，每条语句都有确定的含义，不会出现二义性） ③ 可行性（每一步都能够通过执行有限次数完成） ④ 输入/输出（至少具备 0或n个输入 以及 1或n个输出）

2. 优算法的判断标准① 正确性（ 可运行，无异常，可满足需求） ② 易读性（ 方便阅读，理解、交流） ③ 健壮性（ 对于“非法输入”，“异常” 等 ， 对此有良好的反馈以及解决处理） ④ 高效性 （较少的时间，实现相同的需求） ⑤ 低存储性 （算法所需要的存储空间小，算法所占空间被称为“空间复杂度”）

3. 时间复杂度① 不同的算法 ，所需 时间 以及 空间 不同。 ② 同一种算法，在 不同的设备上，运行效率 不同。所以我们要比较算法的时候，建议在 同一设备 上进行对比测试。 ③ 除此之外，算法还受 编写语言 的影响。（编译语言比解释语言快）观看下面这一段代码#include<iostream>usingnamespace std;inttest(int);intmain(){ cout<<"开始执行。。。"<<endl;//执行一次 test(13);//进入test(int) 函数中。 cout<<"执行完毕"<<endl;//执行一次 return0;}inttest(int n){for(int j =1;j<=n;j++)//注意将会执行n+1次，并非n次。 最后还会进行一次判断。 for(int i =1;i<=n;i++)//执行n(n+1) 次 cout<<"i:"<<i<<endl;//执行n²次}上面例子中 ： 共执行了 1+1+1+(n+1)+n(n+1)+n² = 2n²+2n+4次 ，使用函数T()表示T(n) = 2n²+2n+4测试：#include<iostream>usingnamespace std;// 2n²+2n+4doublefun(int);// 2n²+2ndoublefun2(int);// 2n²doublefun3(int);// n²doublefun4(int);intmain(){// n = 10; cout<<"当n=10: "<<endl <<"2(n^2)+2n+4精确值 --> "<<fun(10)<<endl <<"其中：2(n^2)+2n占-->"<<fun2(10)<<endl <<"其中：2(n^2)占 -->"<<fun3(10)<<endl <<"其中 n^2 占 -->"<<fun4(10)<<endl<<endl <<"比重情况:"<<endl <<"fun2(10)："<<fun2(10)/fun(10)<<endl <<"fun3(10)："<<fun3(10)/fun(10)<<endl <<"fun4(10)："<<fun4(10)/fun(10)<<endl <<endl<<endl; cout<<"================================"<<endl;// n = 555; cout<<"当n=5555: "<<endl <<"2(n^2)+2n+4精确值 --> "<<fun(5555)<<endl <<"其中：2(n^2)+2n占-->"<<fun2(5555)<<endl <<"其中：2(n^2)占 -->"<<fun3(5555)<<endl <<"其中 n^2 占 -->"<<fun4(5555)<<endl<<endl <<"比重情况:"<<endl <<"fun2(5555)："<<fun2(5555)/fun(5555)<<endl <<"fun3(5555)："<<fun3(5555)/fun(5555)<<endl <<"fun4(5555)："<<fun4(5555)/fun(5555)<<endl <<endl<<endl; cout<<"================================"<<endl;// n = 9999; cout<<"当n=9999: "<<endl <<"2(n^2)+2n+4精确值 --> "<<fun(9999)<<endl <<"其中：2(n^2)+2n占-->"<<fun2(9999)<<endl <<"其中：2(n^2)占 -->"<<fun3(9999)<<endl <<"其中 n^2 占 -->"<<fun4(9999)<<endl<<endl <<"比重情况:"<<endl <<"fun2(9999)："<<fun2(9999)/fun(9999)<<endl <<"fun3(9999)："<<fun3(9999)/fun(9999)<<endl <<"fun4(9999)："<<fun4(9999)/fun(9999)<<endl <<endl<<endl;return0;}/* 方法实现 */doublefun(int n){return2*(n*n)+2*n+4;}doublefun2(int n){return2*(n*n)+2*n;}doublefun3(int n){return2*(n*n);}doublefun4(int n){return n*n;}运行结果：

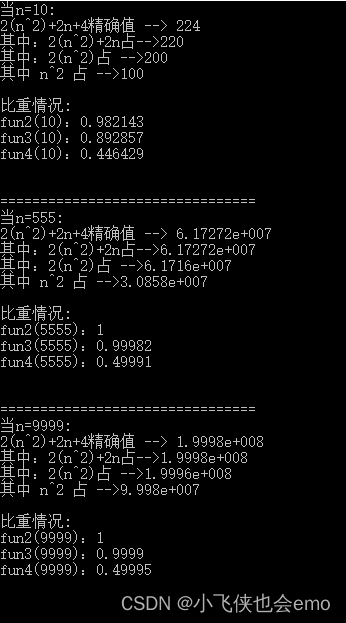
通过上面的例子，不难发现：n值越大，n²和2n²越贴近精确值。
最离谱的是，当n=9999时 ， 
    （1）2n²+2n 几乎等于 精确值 。
    （2）2n² 占比 0.9999。
    （3）其中 n²就占0.49995。
    所以在式子中 n² 的增长速度是最快的。
试想一下：当n=999999999999时 ， n² 占 精确值 的多少呢？

计算时间复杂度,我们不需要太多精准的值，我们的目的是在于比较两个算法的优异程度。

所以上面的式子中，我们可以写作为T(n) = n²

“时间复杂度” 则记作 ：**T(n) = O(f(n))**。 f(n) 是 式子 中n 的某个函数。 这就是“ 大O计法”

使用“ 大O计法”表示则为 ：Ｏ(n²)

① 常数阶

intmain(){int i =4;//执行一次 
    cout<<"i --> "<<i<<end;//执行一次 int b = i +2;//执行一次 
    cout<<"b --> "<<b<<end;//执行一次return0;}

上方程序中，共执行了 f(n) = 1+1+1+1 = 4 次。
使用“大O记法”则为 ： O(f(n)) = O(4) ❌ --> O(f(n)) = O(1) ✔
无论常数是几 ， 我们都记作为1. 就算执行了 100 次。只要是常数阶 那么也记作为O(1)

② 线性阶

for(int i =0;i<n;i++)//代码体中执行了n次{//代码体内容                    }

那么f(n) = n ， 所以其“时间复杂度”为 O(n)

③ 对数阶

inttest(int n){int i =1;while(i < n)//执行次数 = ？
        i *=2;}

变量 i 乘以 多少个2 ， 大于n呢？
可能是10个，也可能是10个 ， 取决与n是多少。
我们假设有x个 ， 那么x = log2n
记作 ：O(logn)

④ 平方阶

inttest(int n){for(int i =0;i<n;i++)for(int j =0;j<n;j++)//我是代码体                    //执行次数n*n次

其“时间复杂度”为 ： O(n²)

后面我们还会介绍一种可怕的“时间复杂度”

1. 最好、最坏、平均 的执行情况什么？ 这东西还分 最好，最坏，平均 的情况？？？其实也没这么复杂，其中有两种情况我们不管。吆西，我懂了，无论什么情况，我们都要做好最坏的打算，以方便应付意外的事情，是这样吗？你很聪明呀，我们继续往下看。 给大家讲个例子：今天老师说调位置，恰好班级里面有一位长相极美的女生。最好的情况：她是我同桌。中肯的情况：我俩相隔的距离占总距离的 1/2。最坏的情况：我当上了 “舔狗”。带入到程序中：/** 模拟strchr()*/char*strchr(char* s,char i){while(*s++!='\0')if(*s == i)return s;returnNULL;}如果我们运气好的话，第一次就找到了 变量 i，如果运气不好呢？那可能 i 在 s的结尾位置。中肯一点的话，i 在 s 的中间位置。除非有特殊说明，否则，我们按照 最坏的情况 进行计算。

讲故事咯

有这么一个故事，有一天国王与一个数学家下棋，他不相信这个数学家比他还聪明。
便对数学家，说：你如果赢了，我把国王送给你，但是如果你输了，你就要在全世界面前夸我比你聪明。
对局开始了，第一盘国王输了，国王对数学家说道：并没有规定一局定输赢。
一连下了好几盘，国王都输了，国王也是服气了。
这时，数学家说到：我不要你的国王 ， 我只要米。
国王：米？你要多少
数学家：第一格放一粒米，第二格 放两粒米 ，后一格是上一格的两倍，一次类推。
国王看了看64格的棋盘，笑出了声。
结局我想大家都猜到了。
这个数学家就是 “阿基米德”。

对于上面的例子 1+2+2²+2³+…+263 这种属于爆炸式增长
对于上面的例子，我们可以变成
 S = 1+2+2²+2³+…+263
 2S = 2+2²+2³+…+264
 S = 2+2²+2³+…+264 - 1-2-2²-2³-…-263
  = 264 - 1
我们使用程序进行实现：

 第①方式：时间复杂度 O(n)

intmain(){double num =1;//执行一次for(int i =1;i<=64;i++)//执行n+1次
        num *=2;//O(1) 复杂度
    num--;//执行一次
    cout<<num<<endl;//执行一次return0;}

这样我们很轻松的就算出了答案。

 第②方式：使用O(2n)复杂度进行计算。
如果对这个程序原理感兴趣可以dd我，这里我就不讲解了。

longtest2(int n){staticlong num =0;//总和    staticlong index=1;//层数计算器,层数标识    int count =1;//因为是 (n=2)^n , 所以每次都只循环n=2次 while(count <=2){
        num++;//总数+1 
        cout<<"num -->"<<num<<endl;//方便监控 num 变量if(index!= n)//如果不是最底层 {
            index++;//层数标识+1 test2(n);//递推开始 }
        count++;//循环次数+1 } 
    index--;//层数下移一层. return num/2;// 2S = ...,所以需要除以2 , 求S }

上面那个程序，我从写第一个字就开始执行了，到现在还没有执行完毕，可见其的可怕之处。
（也许国王的泪，如同这个程序一样，瀑布似得往下掉（**滑稽保命!!!**））
以后大家要避免这种算法。

会不会是你的程序有bug啊？
emm… 不排除这个可能,但我更希望你闭嘴

溜了溜了，我们下期见！