堆排序及堆排序应用

前言

现在给你一个无序数组，尝试用一种时间复杂度和空间复杂度尽可能小的方法，对该数组进行升序排序。

这个问题应该说我们在学习c语言的时候就遇到过，我们很容易想到冒泡排序法。冒泡排序法的时间复杂度是O(n^2),效率相对来说比较低今天我们讲述的堆排序可以很好的解决这个问题，把时间复杂度降到O(N*logN).同时给大家分享一下堆排序的一个应用---Topk问题。

堆排序

思路

1.首先我们要将数组变成一个堆的数据结构这里我们可以让数组的元素从前到后依次进行向上调整或者让数组的元素从后向前依次进行向下调整，经过以上操作我们可以得到一个堆。

2.我们接下来不断让堆顶元素跟最后一个元素交换（让最值放到后面），数组元素个数减去一，接着对元素个数减一的数组再进行调整，让它仍然是一个堆。重复以上操作。

经过上述操作后我们就可以对数组进行排序。

向上调整生成堆

下面我们来分析一下向上调整为小堆的方法。

我们知道向上调整需要深度小于该数据深度的数据构成一个小堆，那我们在遍历数据的时候就要从前到后来遍历这样可以一直保持小堆的状态。

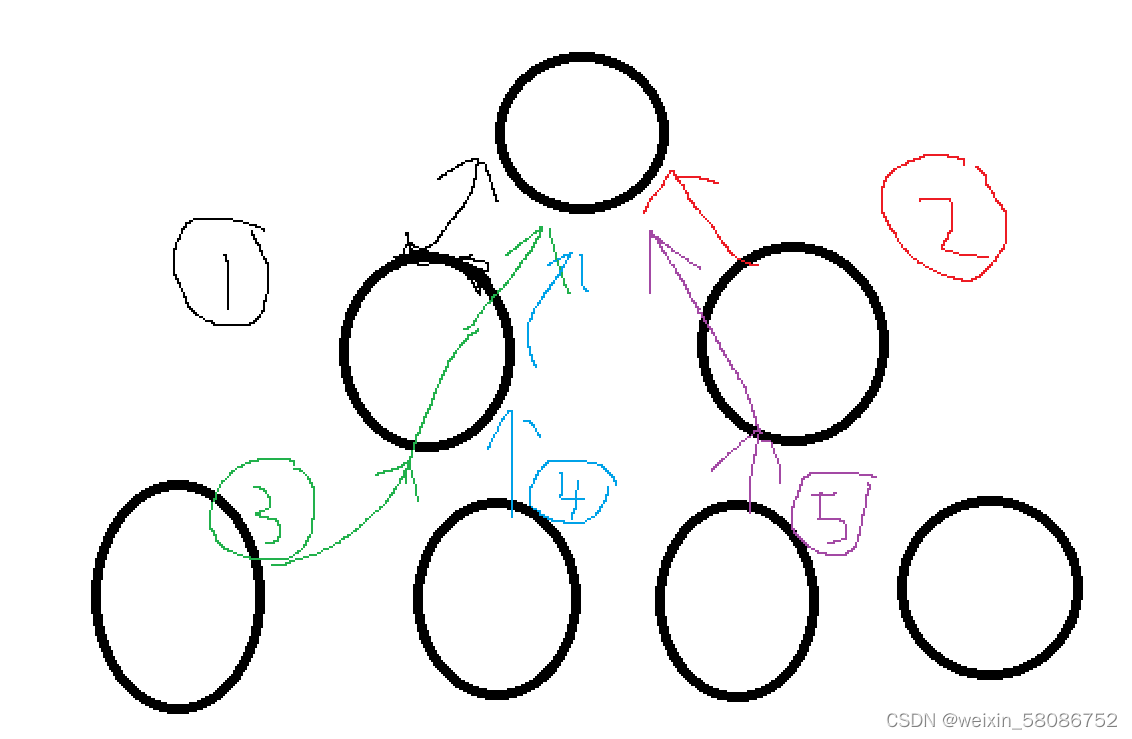
它的时间复杂度是多少呢？

第一层进行了 0次操作

第二层进行了 2*1次操作

第二层进行了 2^2*2次操作

............第h层进行了2^(h-1)*(h-1)

我们发现这是一个等差乘以等比的数列求和问题，设共有n个数那么h=log(n),最后算出来时间复杂度是n*logn。

向下调整生成堆

如果要数据实现向下调整我们就必须保证深度大于的该数据的数据构成一个小堆，那我们就应该从后向前进行遍历。我们看一下这种方法的时间复杂度。

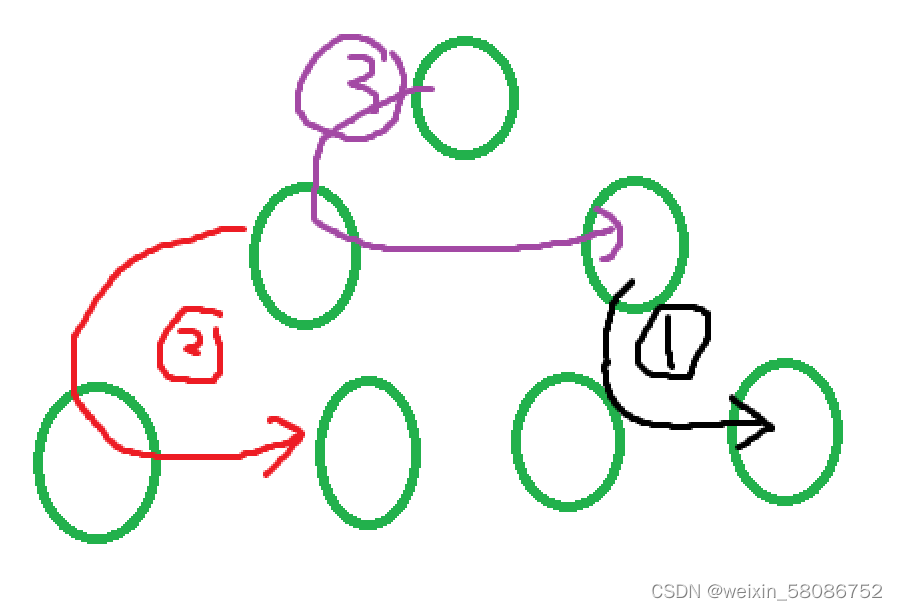
第h层进行了2^(h-1)*(1-1)次操作

第h-1层进行了2^(h-2)*1次操作

,,,,,,,,,,,第1层进行了2^0*(h-1)次操作

这同样也是一个等差乘以等比数列求和问题，我们设数组有n个那么高度就是logn，最后算出来时间复杂度是O(N);

向下调整的算法是比向上调整的算法要优的。所以我们在调整的时候都采用向下调整的算法。

它的代码如下：

void Swap(int* a, int* b)//交换函数
{
    int c = *a;
    *a = *b;
    *b = c;
}
void AdjustDown(int* a, size_t n, size_t num)//从某一元素进行向下调整
{
    assert(a);
    int parent = num;
    int child = num * 2 + 1;
    while (child <= n)
    {
        if (child == n)
        {
            ;
        }
        else
        {
            if (a[child] > a[child + 1])
                child += 1;
        }
        if (a[child] < a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = child * 2 + 1;
        }
        else
        {
            break;
        }
     }
}
void TurnHeap(int* a, size_t size)//把一个数组变成一个堆
{
    assert(a);
    int num = (size - 1 - 1) / 2;
    for (int i = num; i >= 0; i--)
    {
        AdjustDown(a,size,i);
    }
}

排序

接下来就轮到我们排序了，现在无序数组已经变成了一个堆，我们知道堆顶就是是数组中的最值。我们可以把堆顶元素与数组的最后元素交换，然后让堆的size-1，接着让堆顶元素向下调整。这样一个最值排到了最后，依次重复这种操作即可成功排序。

代码实现如下：

void HeapSort(int* a, size_t size)
{
    TurnHeap(a, size);
    size_t count = size - 1;
    while (count > 0)
    {
        Swap(&a[count], &a[0]);
        count--;
        AdjustDown(a, count,0);
    }
}

Topk问题

what is topk

找出N个数里面最大/最小的前K个问题。

比如：未央区排名前10的泡馍，西安交通大学王者荣耀排名前10的韩信，全国排名前10的李白。等等问题都是Topk问题。

思路

思路一：对n个数直接进行堆排序。时间复杂度是O(nlogn)

思路二：把n个数变成一个堆，然后取堆顶，删除堆顶k次时间复杂度为O（n+k*logn）

思路三：（以前最大前k个数为例子）把n个数的前k个数变成一个小（大）堆，然后遍历剩下的n-k个数依次与堆顶元素比较大小，如果比堆顶元素大的话那么交换，并向下调整。时间复杂度是（k+（n-k)*logN）.

通过分析可知思路三提供的算法效率最高。故采用思路三比较好。

代码实现

void HeapSort(int* a, size_t size)
{
    TurnHeap(a, size);
    size_t count = size - 1;
    while (count > 0)
    {
        Swap(&a[count], &a[0]);
        count--;
        AdjustDown(a, count,0);
    }
}

现在我们来进行一个实验

int main()
{
    int a[10000] = {0};
    srand(time(0));
    for (int i = 0; i < 10000; i++)
    {
        a[i] = rand() % 1000 + 1;
    }
    a[51] = 4648946;
    a[15] = 4988954;
    a[16] = 4855665;
    a[55] = 1636889;
    Topk(a, 4, sizeof(a) / sizeof(int));
    for (int i = 0; i < 4; i++)
    {
        printf("%d ", a[i]);
    }
    return 0;
}

这是一个测试函数，把该函数与上述函数放在一块我们ctrl+F5观察结果如下：

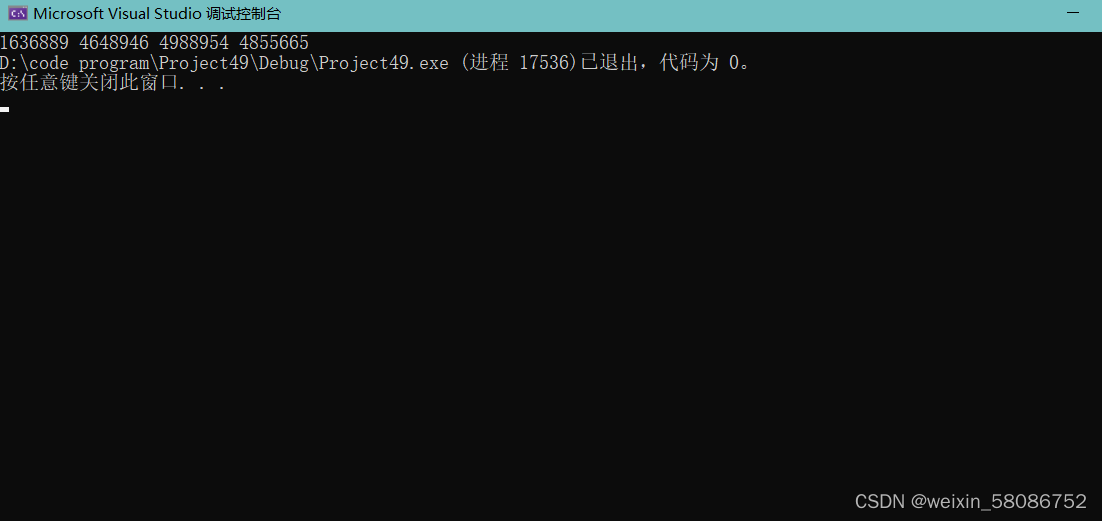
我们成功了