0
0

机器学习分类算法之XGBoost（集成学习算法）

目录

👇👇🧐🧐✨✨🎉🎉

欢迎点击专栏其他文章（欢迎订阅·持续更新中~）

机器学习之Python开源教程——专栏介绍及理论知识概述

机器学习框架及评估指标详解

Python监督学习之分类算法的概述

数据预处理之数据清理，数据集成，数据规约，数据变化和离散化

特征工程之One-Hot编码、label-encoding、自定义编码

卡方分箱、KS分箱、最优IV分箱、树结构分箱、自定义分箱

特征选取之单变量统计、基于模型选择、迭代选择

机器学习分类算法之朴素贝叶斯

【万字详解·附代码】机器学习分类算法之K近邻（KNN）

《全网最强》详解机器学习分类算法之决策树（附可视化和代码）

机器学习分类算法之支持向量机

机器学习分类算法之Logistic 回归（逻辑回归）

机器学习分类算法之随机森林（集成学习算法）

持续更新中~

作者简介

👦博客名：****王小王-123

👀简介：CSDN博客专家、CSDN签约作者、华为云享专家，腾讯云、阿里云、简书、InfoQ创作者。公众号：书剧可诗画，2020年度CSDN优秀创作者。左手诗情画意，右手代码人生，欢迎一起探讨技术

走进XGBoost

什么是XGBoost？

  • 全称：eXtreme Gradient Boosting
  • 作者：陈天奇(华盛顿大学博士)
  • 基础：GBDT
  • 所属：boosting迭代型、树类算法。
  • 适用范围：分类、回归
  • 优点：速度快、效果好、能处理大规模数据、支持多种语言、支持自定义损失函数等等。
  • 缺点：算法参数过多，调参负责，对原理不清楚的很难使用好XGBoost。不适合处理超高维特征数据。

XGBoost是陈天奇等人开发的一个开源机器学习项目，高效地实现了GBDT算法并进行了算法和工程上的许多改进，被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。

说到XGBoost，不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT，但是力争把速度和效率发挥到极致，所以叫X (Extreme) GBoosted。

XGBoost树的定义

先来举个例子，我们要预测一家人对电子游戏的喜好程度，考虑到年轻和年老相比，年轻更可能喜欢电子游戏，以及男性和女性相比，男性更喜欢电子游戏，故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分，如下图所示。

5574d37da77648519760793d6eafb254.png​

就这样，训练出了2棵树tree1和tree2，类似gbdt的原理，两棵树的结论累加起来便是最终的结论，所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加：2 + 0.9 = 2.9。爷爷的预测分数同理：-1 + （-0.9）= -1.9。具体如下图所示：

8de7e5c9a65b4cfbae190943954288da.png​

a02404a389c4474884c9255ca38eb7f1.png​** 这个图形也可以使用XGBoost自带方法可视化，和上面那个预测图一样的意义**

如果你对gbdt有所了解，你会发现这不是一样的吗？

事实上，如果不考虑工程实现、解决问题上的一些差异，XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示：

d75e13b973cd4b8ea562a48ed102b361.png​

如果光看这一张图片，你也许会有所疑惑，这些到底是什么？

红色箭头所指向的L 即为损失函数（比如平方损失函数：l(yi,yi)=(yi−yi)2)
红色方框所框起来的是正则项（包括L1正则、L2正则）
红色圆圈所圈起来的为常数项
对于f(x)，XGBoost利用泰勒展开三项，做一个近似。f(x)表示的是其中一颗回归树。

再举一个简单的例子

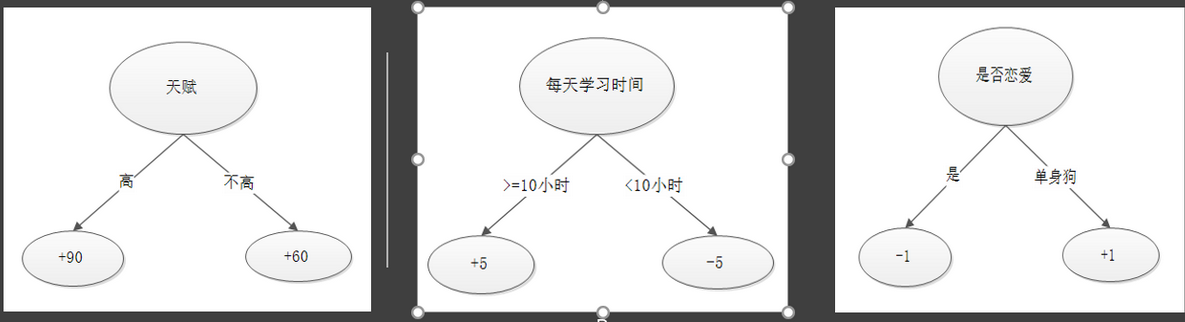6e6fd585750048b9a6b99cf0b717afc5.png​ 首先我们初始化三个样例的考试成绩预测值为0，属性为（天赋高、不恋爱、每天学习时间有16个小时），（天赋低、不恋爱、每天学习时间有16个小时），（天赋高、不恋爱、每天学习时间有6个小时），真实成绩分别为100，70，86分。

Xgboost系统的每次迭代都会构建一颗新的决策树，决策树通过与真实值之间残差来构建，（天赋高、不恋爱、每天学习时间有16个小时）的学霸考了100分，（天赋低、不恋爱、每天学习时间有16个小时）的小学霸考了70分，（天赋高、不恋爱、每天学习时间有6个小时）的小天才考了86分，那么三位同学通过第一个决策树后预测结果分别为90分，60分，和90分。

在构建第二颗决策树时就会考虑残差（100-90=10），（70-60）=10，（86-90=-4）来构建一颗新的树，我们通过最小化残差学习到一个通过学习时间属性来构建的决策树的得到90+5，60+5，90-5的预测值，再继续通过（100-95=5）（70-65）（86-85）的残差构建下一个决策树，以此类推，当迭代次数达到上限或是残差不再减小是停止，就得到一个拥有多个（迭代次数）决策树的强分类器。

当然分类器是需要考虑更多样本的，我们可以把新加入的决策树fi（x）看作是在N维空间（因为有N个样本）中p（m）相对于点p（m-1）的增量。

XGBoost核心算法

  1. 不断地添加树，不断地进行特征分裂来生长一棵树，每次添加一个树，其实是学习一个新函数**f(x)**，去拟合上次预测的残差。
  2. 当我们训练完成得到k棵树，我们要预测一个样本的分数，其实就是根据这个样本的特征，在每棵树中会落到对应的一个叶子节点，每个叶子节点就对应一个分数
  3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。

为了保证预测值和真实值的匹配

XGBoost也是需要将多棵树的得分累加得到最终的预测得分（每一次迭代，都在现有树的基础上，增加一棵树去拟合前面树的预测结果与真实值之间的残差），在前面也提到过。

d949f12d24614a9b9ca7c20b0f5ebf50.png​

那接下来，我们如何选择每一轮加入什么 f 呢？答案是非常直接的，选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。

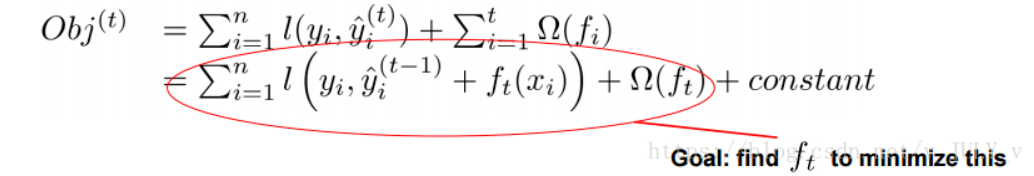
21e83fca382a4f72b87da5157af0a588.png​

实质是把样本分配到叶子结点会对应一个obj，优化过程就是obj优化。也就是分裂节点到叶子不同的组合，不同的组合对应不同obj，所有的优化围绕这个思想展开。

到目前为止我们讨论了目标函数中的第一个部分：训练误差；下面就开始讨论目标函数的第二个部分：正则项，即如何定义树的复杂度。

正则项：树的复杂程度

XGBoost的复杂程度包含了两个重要的部分，一个是树里面叶子节点的个数T，一个是树上叶子节点的得分w的L2模平方（对w进行L2正则化，相当于针对每个叶结点的得分增加L2平滑，目的是为了避免过拟合）

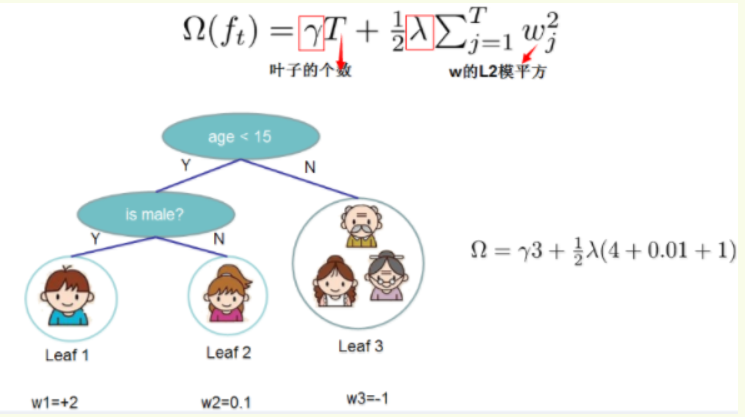
89903c8126c74e5bbc777f05fe127b8d.png​

XGBoost的目标函数（损失函数揭示训练误差 + 正则化定义复杂度）：

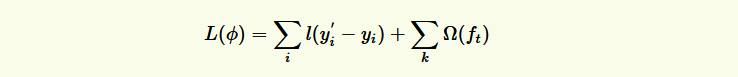
fc8325b0b26e44b0b557e09ca0062d99.png​

总而言之，XGBoost使用了和CART回归树一样的想法，利用贪婪算法，遍历所有特征的所有特征划分点，不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益，同时为了限制树生长过深，还加了个阈值，只有当增益大于该阈值才进行分裂。从而继续分裂，形成一棵树，再形成一棵树，每次在上一次的预测基础上取最优进一步分裂/建树。

6df3fafd2eee40b7bfddc8f4622617e6.png​

XGBoost与GBDT有什么不同

  1. GBDT是机器学习算法，XGBoost是该算法的工程实现。
  2. 在使用CART作为基分类器时，XGBoost显式地加入了正则项来控制模 型的复杂度，有利于防止过拟合，从而提高模型的泛化能力。
  3. GBDT在模型训练时只使用了代价函数的一阶导数信息，XGBoost对代价函数进行二阶泰勒展开，可以同时使用一阶和二阶导数。
  4. 传统的GBDT采用CART作为基分类器，XGBoost支持多种类型的基分类器，比如线性分类器。
  5. 传统的GBDT在每轮迭代时使用全部的数据，XGBoost则采用了与随机森林相似的策略，支持对数据进行采样。
  6. 传统的GBDT没有设计对缺失值进行处理，XGBoost能够自动学习出缺 失值的处理策略。

XGBoost需要注意的点

是否需要做特征筛选？

XGBoost可以做特征筛选，也就是重要性特征排序，那么我们的模型算法需要做特征筛选吗？根据经验来说是不一定，有时候不去剔除反而是最好的，看到网上帖子有一个生动形象的表达：

对于有惩罚项的机器学习算法，不需要，特征选择更多见到的是逻辑回归这种有考虑置信区间的算法，因为要考虑置信区间（达不到95%以上的可信度我就不要了），所以要做特征取舍，因为要做特征取舍，所以要考虑多重共线性问题，因为共线性会直接影响特征的重要性表现。

事实上也是如此，在前期的几个文章里面，我们基于决策树，随机森林等做的特征筛选，反而没有提高模型的效果，还降低了。

对于你不清楚的特征，需要谨慎。因为这有可能是只有短期有效的垃圾特征。
比如瓜长得大不大，跟国足踢球进没进，就大概率没关系。但有可能在特定的农场里有用，比如这个农场的管理员是个球迷，国足踢球踢进了，他就开心，就额外多施肥。那么“国足踢球进没进”这个特征在这个农场里就是一个有力的特征，但放到其他农场里就没用了，这就是一个泛化能力很弱的特征。这样100个不同类型的特征进行删减，可能只有两三个是有用的。

是否需要对数据集归一化？

“答案是不需要。首先,归一化是对连续特征来说的。那么连续特征的归一化,起到的主要作用是进行数值缩放。数值缩放的目的是解决梯度下降时,等高线是椭圆导致迭代次数增多的问题。而xgboost等树模型是不能进行梯度下降的,因为树模型是阶越的,不可导。树模型是通过寻找特征的最优分裂点来完成优化的。由于归一化不会改变分裂点的位置,因此xgboost不需要进行归一化。”

XGBoost重要参数详解

1、booster [default=gbtree]

选择每次迭代过程中需要运行的模型，一共有两种选择：gbtree:；tree-based models，但是一般选择是树，线性不是很好

2、eta [default=0.3, alias: learning_rate]

学习率，可以缩减每一步的权重值，使得模型更加健壮：典型值一般设置为：0.01-0.2

越大，迭代的速度越快，算法的极限很快被达到，有可能无法收敛到真正的最佳。 越小，越有可能找到更精确的最佳值，更多的空间被留给了后面建立的树，但迭代速度会比较缓慢。

3、min_child_weight [default=1]

定义了一个子集的所有观察值的最小权重和。这个可以用来减少过拟合，但是过高的值也会导致欠拟合，因此可以通过CV来调整min_child_weight。

4、max_depth [default=6]

树的最大深度，值越大，树越复杂。这个可以用来控制过拟合，典型值是3-10。

5、gamma [default=0, alias: min_split_loss]

这个指定了一个结点被分割时，所需要的最小损失函数减小的大小。这个值一般来说需要根据损失函数来调整。

6、alpha [default=0, alias: reg_alpha]

L1正则化（与lasso回归中的正则化类似：传送门）这个主要是用在数据维度很高的情况下，可以提高运行速度。

7、objective [default=reg:linear]

这个主要是指定学习目标的：而分类，还是多分类或者回归
“reg:linear” –linear regression：回归
“binary:logistic”：二分类
“multi:softmax” ：多分类，这个需要指定类别个数

d80e0c3645ab40038e8ec41b951e18da.png​

8、subsample有放回随机抽样

我们都知道树模型是天生过拟合的模型，并且如果数据量太过巨大，树模型的计算会非常缓慢，因此，我们要对我们的原始数据集进行有放回抽样(bootstrap)。有放回的抽样每次只能抽取一个样本，若我们需要总共N个样本，就需要抽取N次。每次抽取一个样本的过程是独立的，这一次被抽到的样本会被放回数据集中，下一次还可能被抽到，因此抽出的数据集中，可能有一些重复的数据。
sklearn的随机森林类中也有名为boostrap的参数来帮助我们控制这种随机有放回抽样。同时，这样做还可以保证集成算法中的每个弱分类器（每棵树）都是不同的模型，基于不同的数据建立的自然是不同的模型，而集成一系列一模一样的弱分类器是没有意义的。

在sklearn中，我们使用参数subsample来控制我们的随机抽样。在xgb和sklearn中，这个参数都默认为1且不能取到0，这说明我们无法控制模型是否进行随机有放回抽样，只能控制抽样抽出来的样本量大概是多少。

c3ed188903ee4e31870ac7c7b9bc1938.png​

从这个角度来看，我们的subsample参数对模型的影响应该会非常不稳定，大概率应该是无法提升模型的泛化能力的，但也不乏提升模型的可能性。

数据集过少，降低抽样的比例反而让数据的效果更低，不如就让它保持默认

算法参数过多，调参复杂，对原理不清楚的很难使用好XGBoost，这也是为什么XGBoost好，但是很多人却用不好的原因之一，首先调参就是一个难题

调参步骤及思想

  • 选择较高的学习速率(learning rate)。一般情况下，学习速率的值为0.1。但是，对于不同的问题，理想的学习速率有时候会在0.05到0.3之间波动。选择对应于此学习速率的理想决策树数量。XGBoost有一个很有用的函数“cv”，这个函数可以在每一次迭代中使用交叉验证，并返回理想的决策树数量。
  • 对于给定的学习速率和决策树数量，进行决策树特定参数调优(max_depth, min_child_weight, gamma, subsample, colsample_bytree)。在确定一棵树的过程中，我们可以选择不同的参数，待会儿我会举例说明。
  • xgboost的正则化参数的调优。(lambda, alpha)。这些参数可以降低模型的复杂度，从而提高模型的表现。
  • 降低学习速率，确定理想参数。

XGBoost代码案例

XGBoost效果确实不错，但是前提是要将参数不断地优化和调整，这样最终才能得到一个较好的模型，下面依然以一个实际的案例进行XGBoost代码演示

#导入所需要的包from sklearn.metrics import precision_score
from sklearn.model_selection import train_test_split
import xgboost as xgb
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report
from sklearn.model_selection import GridSearchCV #网格搜索import matplotlib.pyplot as plt#可视化import seaborn as sns#绘图包# 忽略警告import warnings
warnings.filterwarnings("ignore")

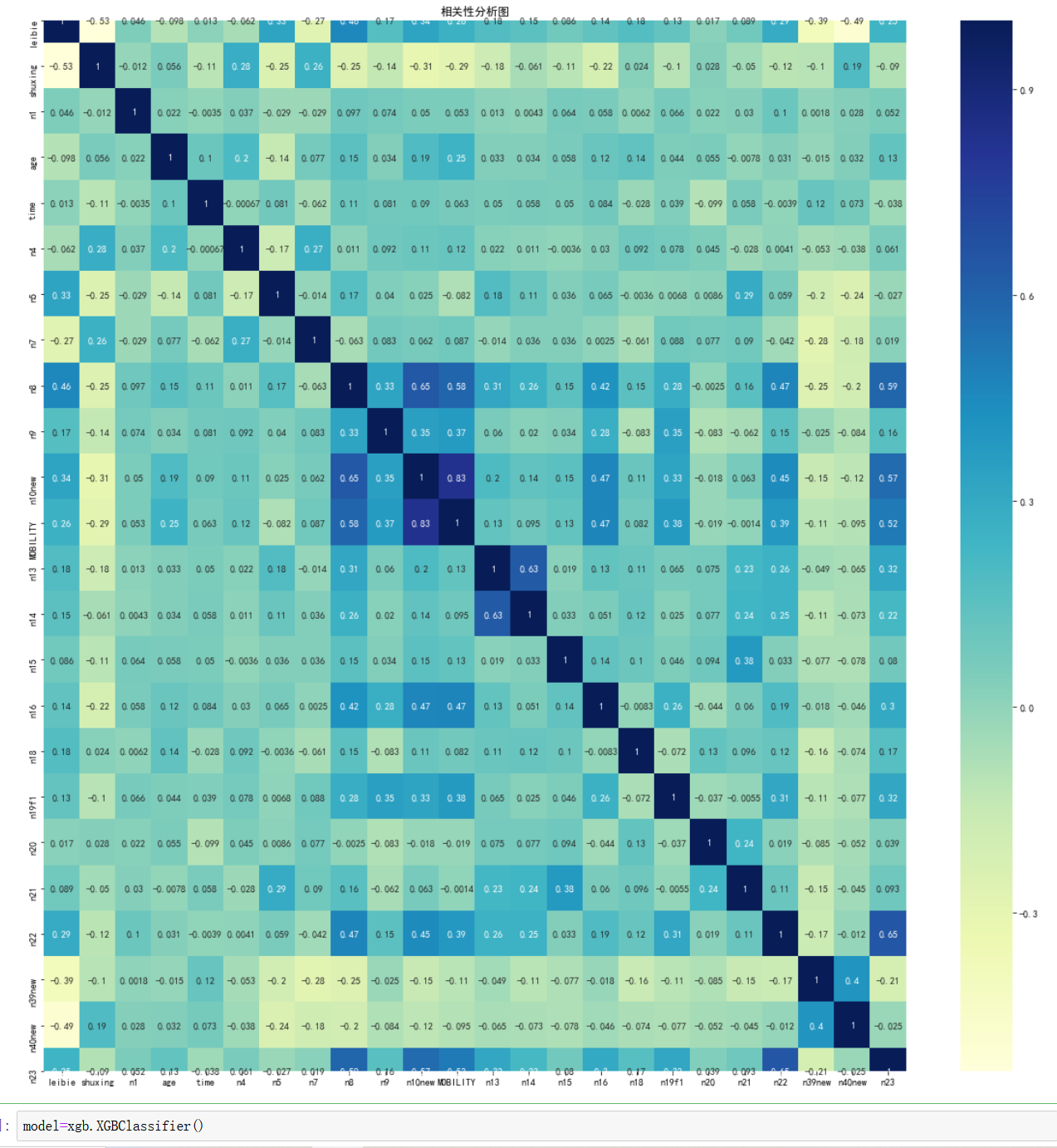
相关性分析

plt.figure(figsize=(20,20))
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
sns.heatmap(df.corr(),cmap="YlGnBu",annot=True)
plt.title("相关性分析图")

be8f2f314f09400983a65850eb90fd10.png​

XGBoost无参数模型

model=xgb.XGBClassifier()
# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)

'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为：', true)
print('预测错的的结果数目为：', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为： {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为：{:.4}%'.format(
      precision_score(y_test,y_pred)*100))
print('预测数据的召回率为：{:.4}%'.format(
      recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为：", f1score_train)
print('预测数据的F1值为：',
      f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为：',
      cohen_kappa_score(y_test,y_pred))
# 打印分类报告
print('预测数据的分类报告为：','
',
      classification_report(y_test,y_pred))

b24ecc3402a44634a4da6e53bfea921f.png​

效果还是不错，比之前用其他的模型反复的调优的效果还好，但是这不是XGBoost的最终效果

n_estimators（学习曲线）

scorel = []
for i inrange(0,300,10):
    model = xgb.XGBClassifier(n_estimators=i+1,
                                 n_jobs=--4,
                                 random_state=90).fit(X_train,y_train)
    score = model.score(X_test,y_test)
    scorel.append(score)

print(max(scorel),(scorel.index(max(scorel))*10)+1)  #作图反映出准确度随着估计器数量的变化，51的附近最好
plt.figure(figsize=[20,5])
plt.plot(range(1,300,10),scorel)
plt.show()

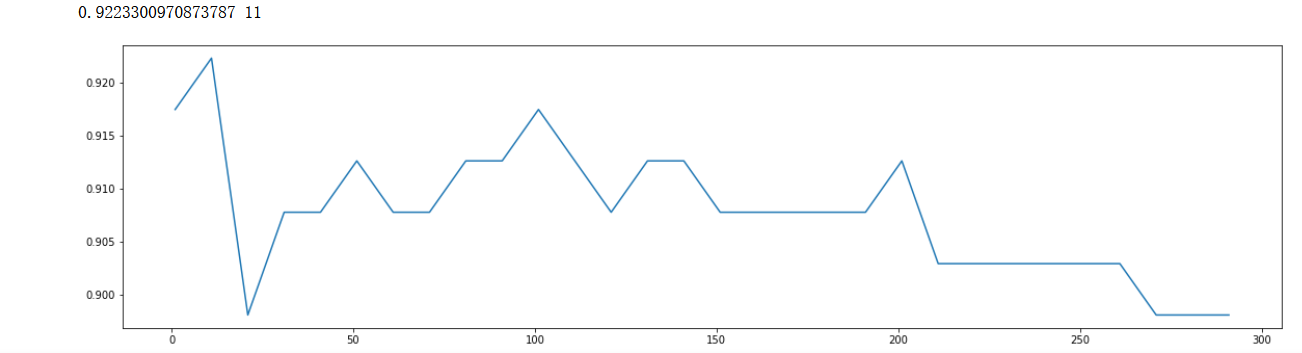
2c75053024084da5b8f10aeffc585ee0.png​

继续迭代优化，缩小范围

scorel = []
for i inrange(0,20,1):
    model = xgb.XGBClassifier(n_estimators=i+1,
                                 n_jobs=--4,
                                 random_state=90).fit(X_train,y_train)
    score = model.score(X_test,y_test)
    scorel.append(score)

print(max(scorel),(scorel.index(max(scorel))*1)+1)  #作图反映出准确度随着估计器数量的变化，51的附近最好
plt.figure(figsize=[20,5])
plt.plot(range(0,20,1),scorel)
plt.show()

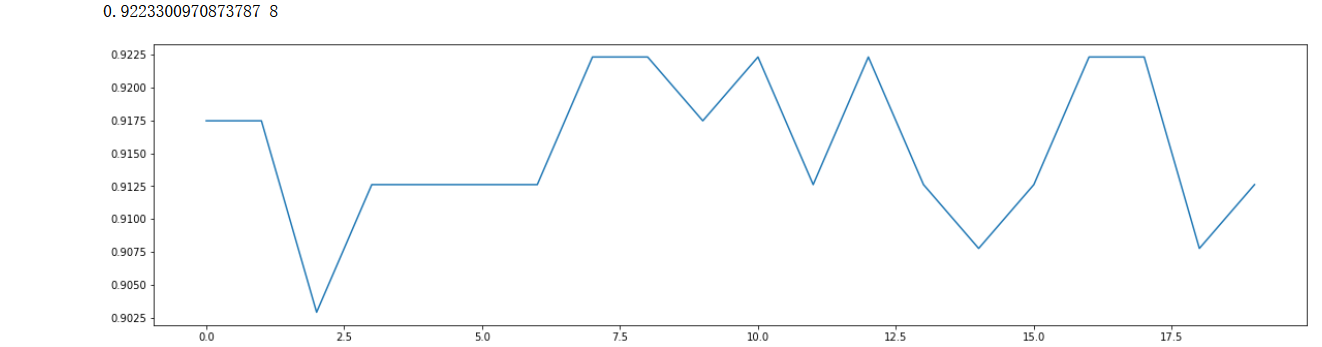
5fce6854b95a4d6ba6471fd1961da105.png​

max_depth（学习曲线）

scorel = []
for i inrange(0,20,1):
    model = xgb.XGBClassifier(max_depth =i,
                                 n_estimators=8,
                                 n_jobs=--4,
                                 random_state=90).fit(X_train,y_train)
    score = model.score(X_test,y_test)
    scorel.append(score)

print(max(scorel),(scorel.index(max(scorel))*1)+1)  #作图反映出准确度随着估计器数量的变化，51的附近最好
plt.figure(figsize=[20,5])
plt.plot(range(0,20,1),scorel)
plt.show()

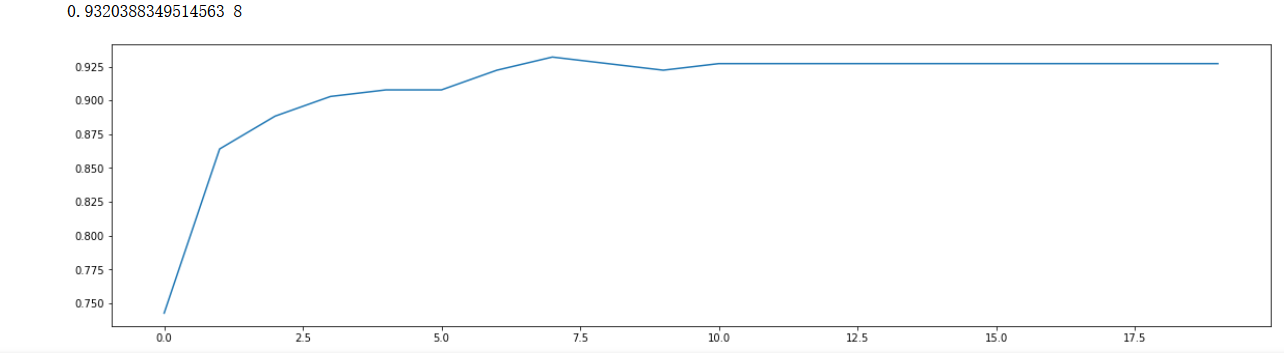
74cb2e9fedbe46e4a888210da83690bb.png​

效果有所提升，继续调优，但是我们知道XGBoost的参数过于的多，如果按照传统的学习曲线迭代调优，效果可能局限在局部最优 ，下面试试XGBoost的交叉验证

调整max_depth 和min_child_weight

param_test1 = {
# 'n_estimators':list(range(3,15,1)),'max_depth':list(range(3,10,2)),
 'min_child_weight':list(range(1,6,2))
}
gsearch1 = GridSearchCV(estimator = xgb.XGBClassifier( learning_rate =0.1, n_estimators=8, max_depth=8,
 min_child_weight=1, gamma=0, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1, seed=27), 
 param_grid = param_test1, scoring='roc_auc',iid=False, cv=5)
gsearch1=gsearch1.fit(X,y)
gsearch1.best_params_, gsearch1.best_score_

({'max_depth': 3, 'min_child_weight': 5}, 0.9200952807471878)

进一步调整

param_test1 = {
 'max_depth':list(range(8,11,1)),
 'min_child_weight':list(range(1,4,1))
}
gsearch1 = GridSearchCV(estimator = xgb.XGBClassifier( learning_rate =0.1, n_estimators=7, max_depth=3,
 min_child_weight=5, gamma=0, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1, seed=27), 
 param_grid = param_test1, scoring='roc_auc',iid=False, cv=5)
gsearch1.fit(X,y)
gsearch1.best_params_, gsearch1.best_score_

({'max_depth': 8, 'min_child_weight': 3}, 0.9158850465045336)

调整gamma

param_test3 = {
 'gamma':[i/10.0for i inrange(0,5)]
}
gsearch3 = GridSearchCV(estimator = xgb.XGBClassifier( learning_rate =0.1, n_estimators=8, max_depth=8,
 min_child_weight=3, gamma=0, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test3, scoring='roc_auc',iid=False, cv=5)
gsearch3.fit(X,y)
gsearch3.best_params_, gsearch3.best_score_

({'gamma': 0.4}, 0.9103697321364825)

调整subsample 和colsample_bytree

param_test5 = {
 'subsample':[i/100.0for i inrange(75,90,5)],
 'colsample_bytree':[i/100.0for i inrange(75,90,5)]
}
gsearch5 = GridSearchCV(estimator = xgb.XGBClassifier( learning_rate =0.1, n_estimators=8, max_depth=8,
 min_child_weight=3, gamma=0.4, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test5, scoring='roc_auc',iid=False, cv=5)
gsearch5.fit(X_train,y_train)
gsearch5.best_params_, gsearch5.best_score_

**({'colsample_bytree': 0.85, 'subsample': 0.85}, 0.9420290874342445)**

效果一下就有了显著的提升，继续调参，因为这个参数还是比较的重要有放回随机抽样

调整正则化参数

param_test6 = {
 'reg_alpha':[1e-5, 1e-2, 0.1, 1, 100]
}
gsearch6 = GridSearchCV(estimator = xgb.XGBClassifier( learning_rate =0.1, n_estimators=8, max_depth=8,
 min_child_weight=3, gamma=0.2, subsample=0.85, colsample_bytree=0.85,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test6, scoring='roc_auc',iid=False, cv=5)
gsearch6.fit(X_train,y_train)
gsearch6.best_params_, gsearch6.best_score_

**({'reg_alpha': 1e-05}, 0.9426155352636133)**

param_test6 = {
 'learning_rate':[0.01, 0.02, 0.1, 0.2]
}
gsearch6 = GridSearchCV(estimator = xgb.XGBClassifier( learning_rate =0.1, n_estimators=8, max_depth=8,
 min_child_weight=1, gamma=0.2, subsample=0.8, colsample_bytree=0.85,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test6, scoring='roc_auc',iid=False, cv=5)
gsearch6.fit(X_train,y_train)
gsearch6.best_params_, gsearch6.best_score_

**({'learning_rate': 0.1}, 0.9506471151048836)**

网格搜索

根据前面所出来的参数，可以进一步的缩放数值，最后采用暴力搜索网格调参，但是由于XGBoost本身就是一个运行速度慢，占据CPU的一个模型，加上网格搜索速度反而变的更慢了，所以这里需要谨慎设置参数，不然电脑会跑的嗡嗡响

# learning_rate =0.1, n_estimators=8, max_depth=8,#  min_child_weight=1, gamma=0.2, subsample=0.8, colsample_bytree=0.85,#  objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27import numpy as np
from sklearn.model_selection import GridSearchCV

parameters = {'n_estimators':np.arange(6,10,1)
              ,'max_depth':np.arange(6,10,1)
              ,"colsample_bytree":np.arange(0.8,0.9,0.05)
              ,"subsample":np.arange(0.8,0.9,0.05)
              ,'gamma':np.arange(0.1,0.5,0.1)
              ,'min_child_weight':np.arange(1,3,1)
}

clf = xgb.XGBClassifier(random_state=25)
GS = GridSearchCV(clf, parameters, cv=5) # cv交叉验证
GS.fit(X_train,y_train)
print(GS.best_params_)
print(GS.best_score_)

{'colsample_bytree': 0.8, 'gamma': 0.4, 'max_depth': 7, 'min_child_weight': 1, 'n_estimators': 8, 'subsample': 0.8}
0.9048780487804878

额，这么说呢，网格搜索的效果还不如自己之前的参数靠谱，事实上说明，我们在优化参数的时候，按照固定思维得出的数值只是一个参考值，我们自己还可以做一些调整（细微的）

最终模型代码

model=xgb.XGBClassifier(eta =0.1, n_estimators=8, max_depth=8,
 min_child_weight=2, gamma=0.8, subsample=0.85, colsample_bytree=0.8)

# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)

'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为：', true)
print('预测错的的结果数目为：', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为： {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为：{:.4}%'.format(
      precision_score(y_test,y_pred)*100))
print('预测数据的召回率为：{:.4}%'.format(
      recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为：", f1score_train)
print('预测数据的F1值为：',
      f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为：',
      cohen_kappa_score(y_test,y_pred))
# 打印分类报告
print('预测数据的分类报告为：','
',
      classification_report(y_test,y_pred))

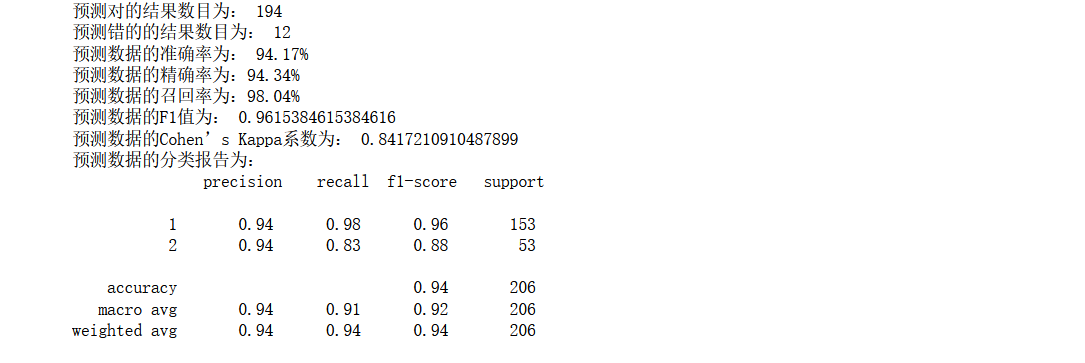
51121d071f06497aa43cdda11b8d7bfe.png​

效果还是不错的，和随机森林有点相近，从这里也可以看出集成学习的优势所在

绘制特征重要性图

from xgboost import plot_importance
# plt.figure(figsize=(15,15))
plt.rcParams["figure.figsize"] = (14, 8)
plot_importance(model)

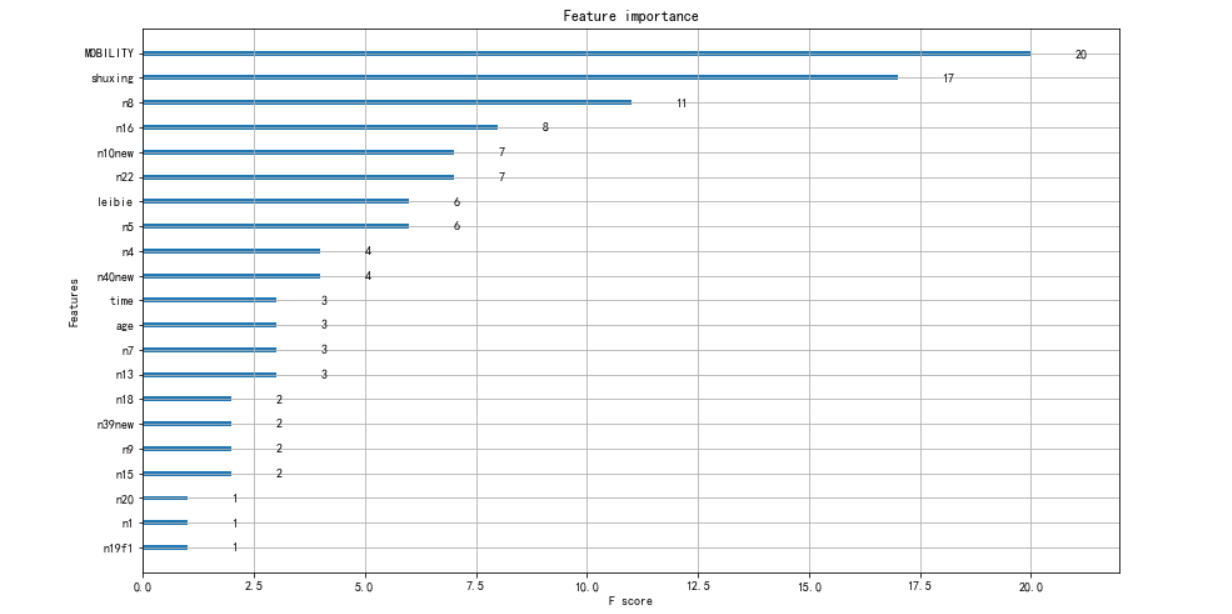
7e4008faea3446919437f672cad16747.png​

XGBoost可视化

xgboosts=xgb.to_graphviz(model)
xgboosts.format = 'png'
xgboosts.view('./xgboost')

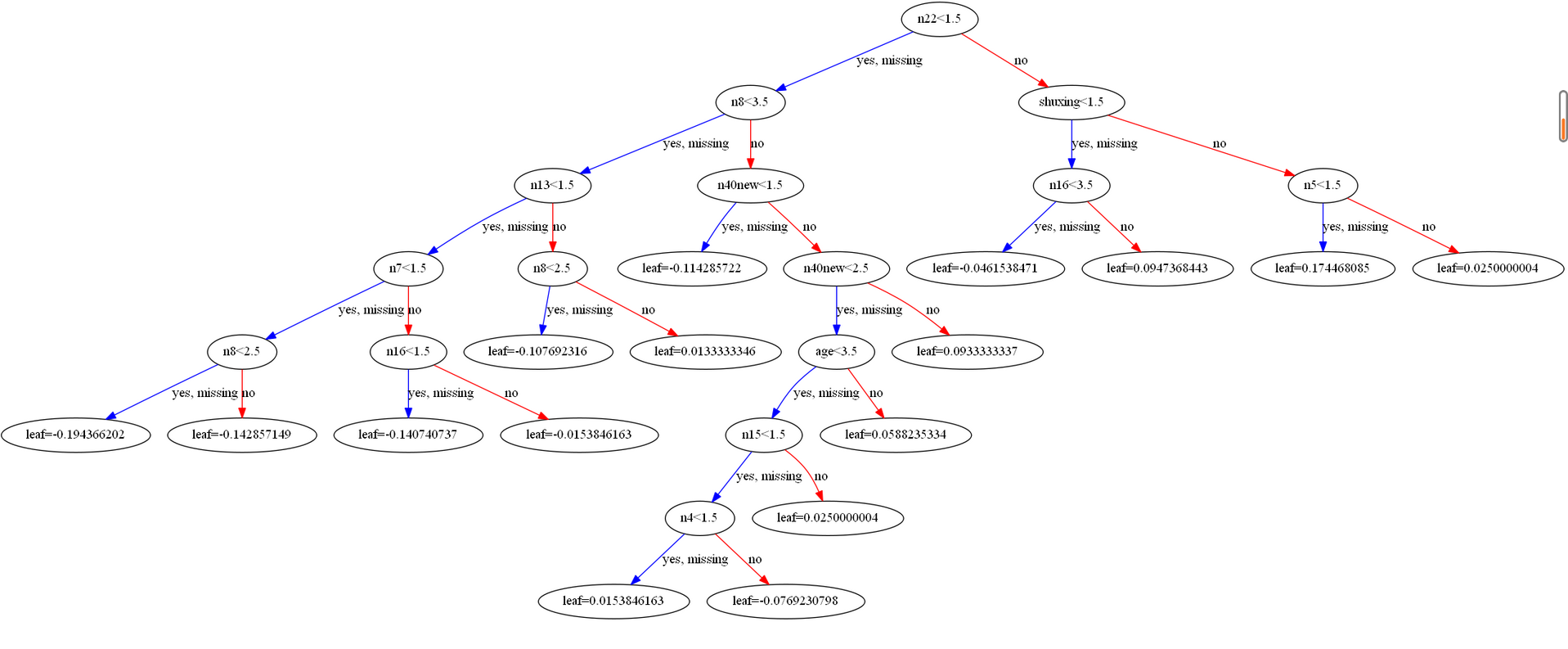
3df79f18e30b4aa28057a8ce16fa8270.png​

这里绘制来一个树的过程，其中leaf代表预测分数

ROC曲线AUC面积

# ROC曲线、AUCfrom sklearn.metrics import precision_recall_curve
from sklearn import metrics
# 预测正例的概率
y_pred_prob=model.predict_proba(X_test)[:,1]
# y_pred_prob ,返回两列，第一列代表类别0,第二列代表类别1的概率#https://blog.csdn.net/dream6104/article/details/89218239
fpr, tpr, thresholds = metrics.roc_curve(y_test,y_pred_prob, pos_label=2)
#pos_label，代表真阳性标签，就是说是分类里面的好的标签，这个要看你的特征目标标签是0,1，还是1,2
roc_auc = metrics.auc(fpr, tpr)  #auc为Roc曲线下的面积# print(roc_auc)
plt.figure(figsize=(8,6))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.plot(fpr, tpr, 'r',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1.1])
plt.ylim([0, 1.1])
plt.xlabel('False Positive Rate') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('Receiver operating characteristic example')
plt.show()

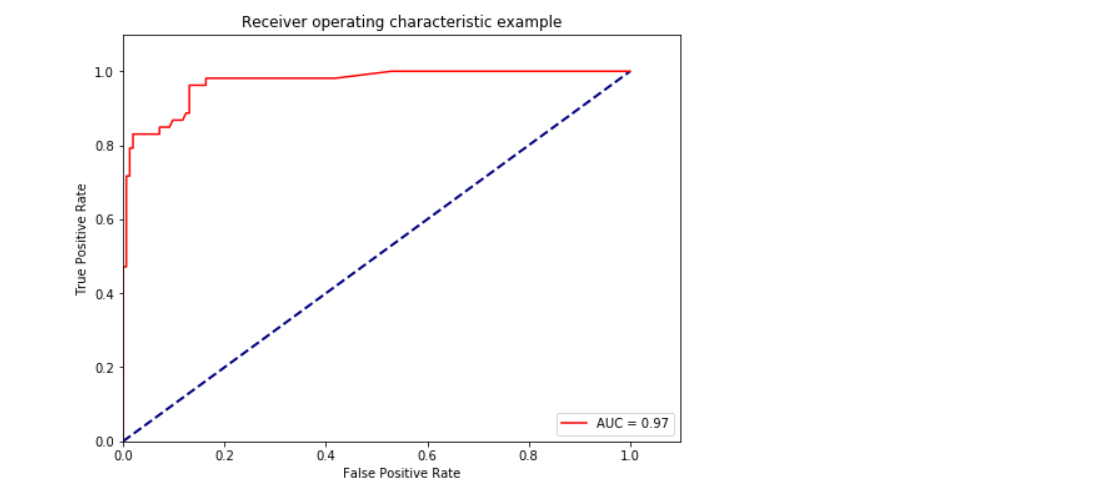
51c5469fcff54730a5d54551c645d9e9.png​

在使用XGBoost的过程中，遇到了很多的参数调优问题，其次就是CPU不足，运行网格搜索的时候，最后有人推荐去使用lightGBM这种轻量级的，但是好像也有数据量的局限性，后期可以测试一下效果。

数据的数量每天都在增加，对于传统的数据科学算法来说，很难快速的给出结果。LightGBM的前缀‘Light’表示速度很快。LightGBM可以处理大量的数据，运行时占用很少的内存。另外一个理由，LightGBM为什么这么受欢迎是因为它把重点放在结果的准确率上。LightGBM还支持GPU学习，因此，数据科学家广泛的使用LightGBM来进行数据科学应用的部署。
不建议在小数据集上使用LightGBM。LightGBM对过拟合很敏感，对于小数据集非常容易过拟合。对于多小属于小数据集，并没有什么阈值，但是从我的经验，我建议对于10000+以上的数据的时候，再使用LightGBM。

每文一语

忙碌也是一种充实的快乐！

标签： 机器学习 分类 xgboost
本文转载自: https://blog.csdn.net/weixin_47723732/article/details/122870062
版权归原作者 王小王-123 所有， 如有侵权，请联系我们删除。
登录后发布评论

“机器学习分类算法之XGBoost（集成学习算法）”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

网络安全法-网络运行安全

使用selenium/drissionpage时如何阻止chrome自动跳转http到https

docker desktop 里部署的Open WebUI 管理员密码忘记了的处理方法

在ubuntu20.04中搭建onsite比赛运行环境

利用开源的低代码表单设计器FcDesigner高效管理和渲染复杂表单结构

Kafka学习笔记

【前端】浏览器输入url到页面呈现发生了什么？

文章导航