做一些哈密顿算符的补充
后面的是一个向量，但是单独的看这个向量没有意义
需要把这个函数和其他函数放在一起做运算的时候才有意义
梯度 散度 和 旋度
梯度
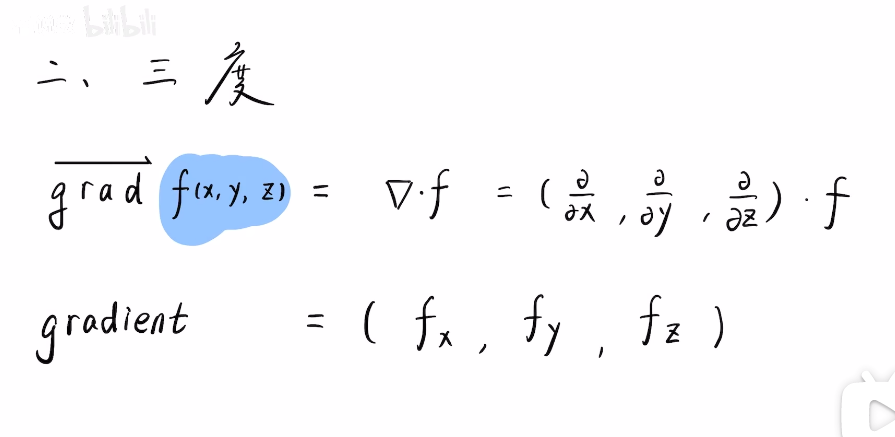蓝色部分是一个标量的梯度
我们用算符乘以这个标量（后面的就是向量乘以标量）
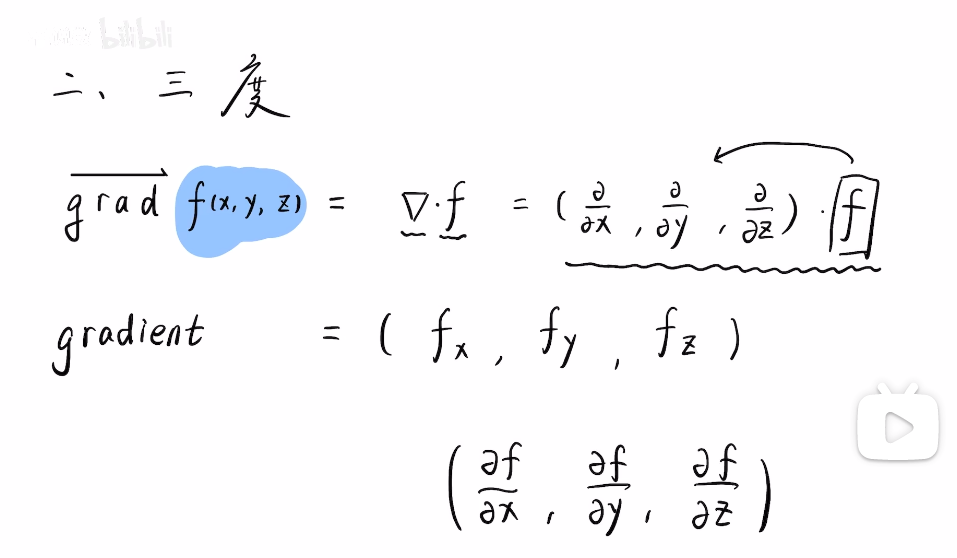我们把f乘进去，得到了f对于x，y，z的导数
散度
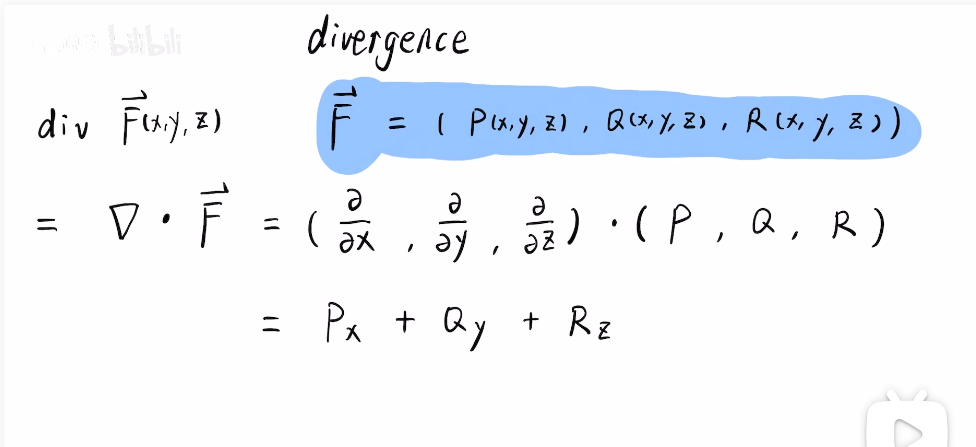散度所处理的这个函数是矢量函数
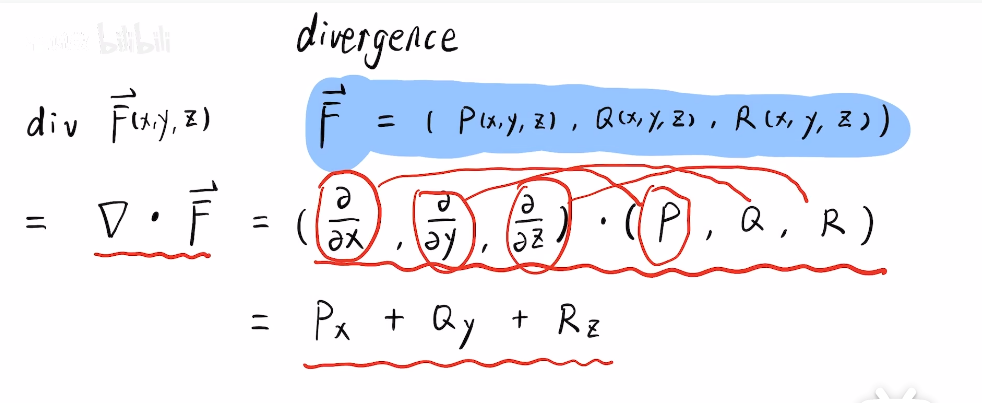我们用这个算子与F（矢量函数），进行点乘（对应位置相乘再相加）
旋度
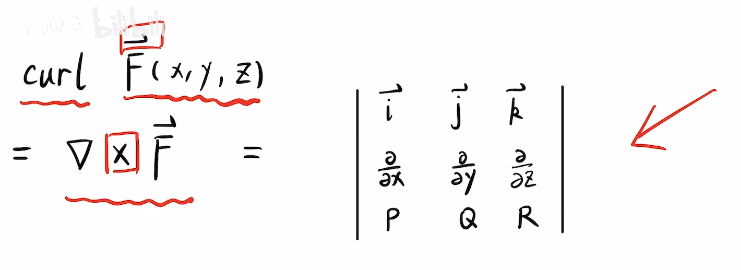
处理的函数也是矢量函数（但是这里是叉乘），散度是点乘，旋度是叉乘
行列式运算下来是一个向量（我一直以为是一个数…）
拉普拉斯算子（正三角形）
是梯度的散度；处理的是一个标量函数
先对f算梯度，然后再对梯度算一下他的散度
就变成了f对x求2阶导（对y、z相同）
我是分割线--------------------
首先区分数量场和向量场
数量场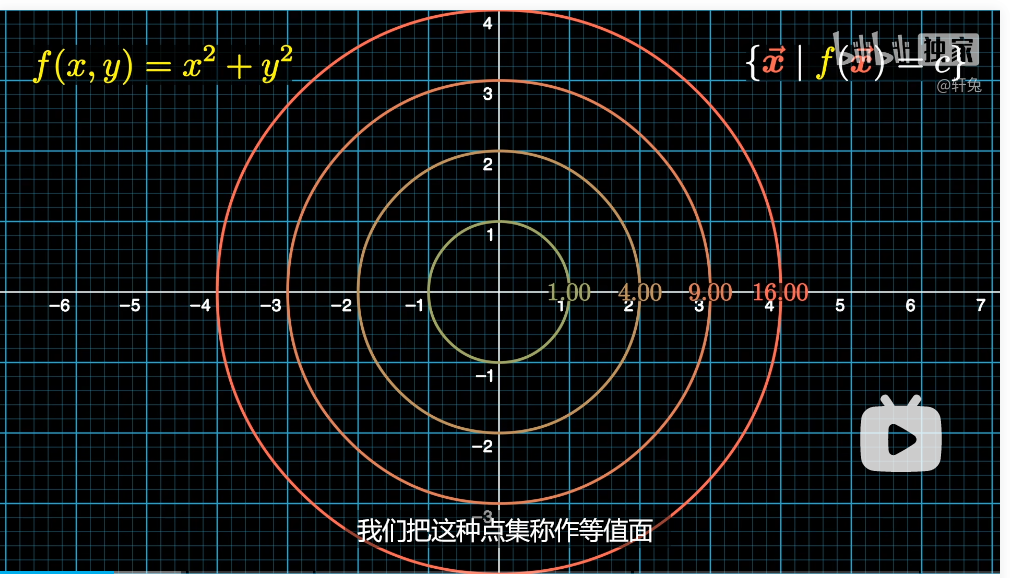
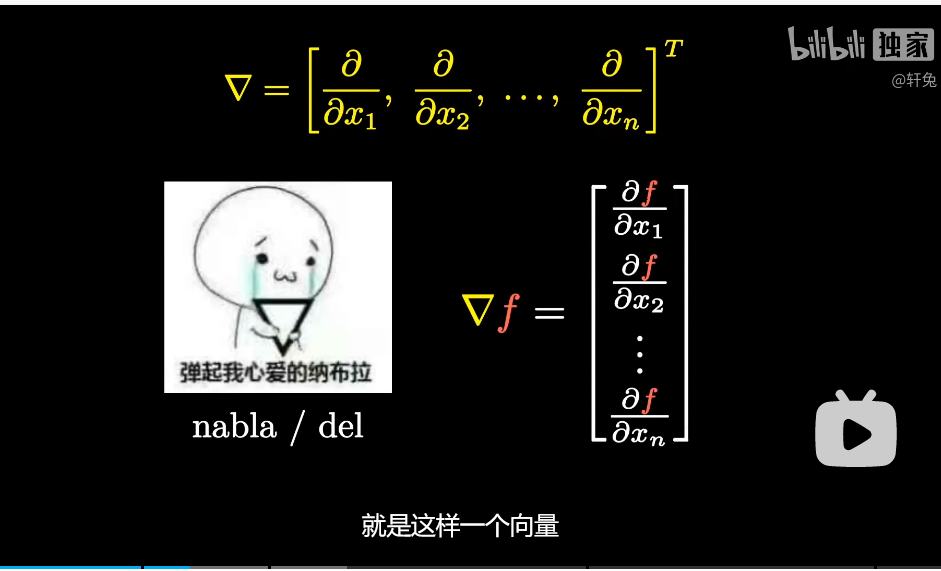
nabla作用于函数之后得到这样一个向量，把数量场变成了向量场
nabla算子通过内积把向量场变成了数量场
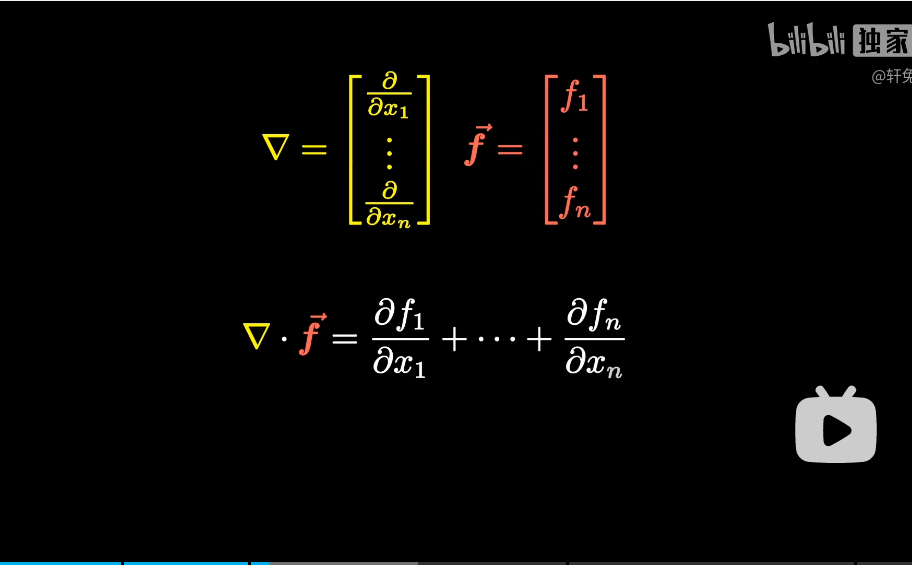散度是2，是一个通量的局部描述（散度是通量的体密度）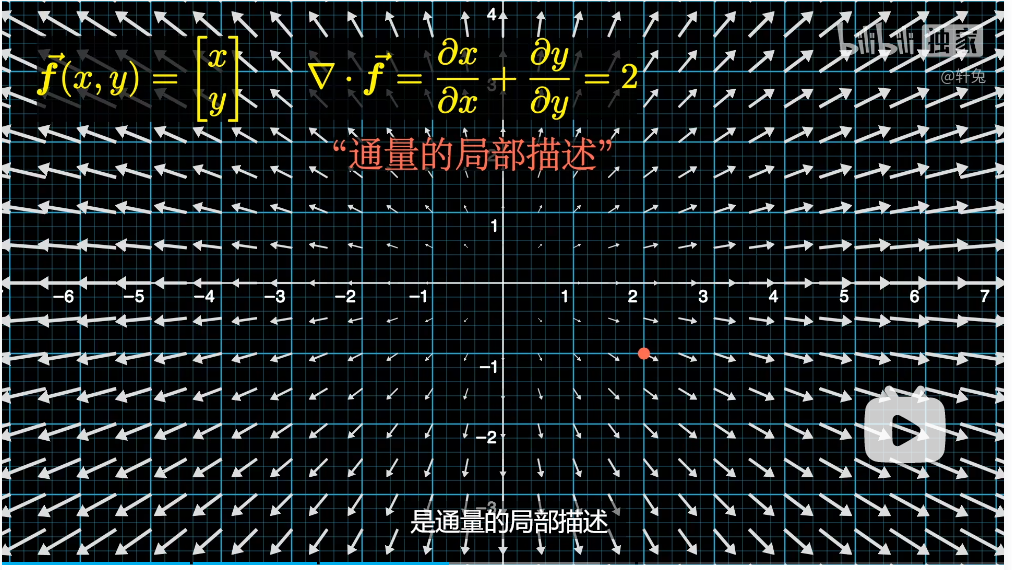
进行叉乘（把向量场变成向量场）
旋度：是环量的局部描述
本文转载自: https://blog.csdn.net/pjm616/article/details/127659438
版权归原作者 小小的石头花花 所有， 如有侵权，请联系我们删除。
版权归原作者 小小的石头花花 所有， 如有侵权，请联系我们删除。