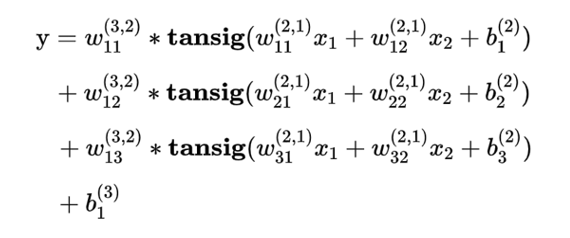BP神经网络的梯度公式推导(三层结构)

本站原创文章，转载请说明来自《老饼讲解-BP神经网络》bp.bbbdata.com

BP神经网络的训练算法基本都涉及到梯度公式，

本文提供三层BP神经网络的梯度公式和推导过程

一. 推导目标

BP神经网络的梯度推导是个复杂活，

在推导之前，本节先把推导目标清晰化

1.1 梯度公式目标

训练算法很多，但各种训练算法一般都需要用到各个待求参数(w,b)在损失函数中的梯度，

因此求出w,b在损失函数中的梯度就成为了BP神经网络必不可少的一环，

求梯度公式，即求以下误差函数E对各个w,b的偏导：

$\displaystyle \displaystyle \textbf{E}(W,b)=\dfrac{1}{M}\sum \limits _{m=1}^{M} \dfrac{1}{K}\sum \limits _{k=1}^{K} (\textbf{f}(\textbf{x})_{km}-\text{y}_{km})^2$

$\textbf{f}(\textbf{x})_{km}$ 代表网络对第m个样本第k个输出的预测值，w,b就隐含在
$\textbf{f}(\textbf{x})$ 中

1.2 本文梯度公式目标

虽然梯度只是简单地求E对w,b的偏导，但E中包含网络的表达式f(x)，就变得非常庞大，

求偏导就成了极度艰巨晦涩的苦力活，对多层结构通式的梯度推导稍为抽象，

本文不妨以最常用的三层结构作为具体例子入手，求出三层结构的梯度公式

即：输入层-隐层-输出层 (隐层传递函数为tansig,输出层传递函数为purelin)

虽然只是三层的BP神经网络，

但梯度公式的推导，仍然不仅是一个体力活，还是一个细致活，

且让我们细细一步一步慢慢来

二. 网络表达式梳理

在损失函数E中包括了网络表达式，在求梯度之前，

先将表达式的梳理清晰，有助于后面的推导

2.1 梳理三层BP神经网络的网络表达式

网络表达式的参考形式
隐层传递函数为tansig,输出层传递函数为purelin的三层BP神经网络，

有形如下式的数学表达式

网络表达式的通用矩阵形式
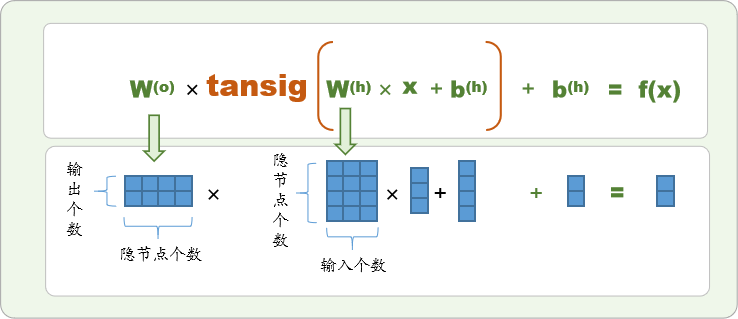
写成通用的矩阵形式为

$\textbf{f}(\textbf{x}) = \textbf{W}^{(o)}\textbf{tansig}(\textbf{W}^{(h)}\textbf{x}+\textbf{b}^{(h)})+\textbf{b}^{(o)}$

这里的
$\textbf{W}$ 为矩阵，
$\textbf{x}$ 和
$\textbf{b}$ 为向量，

上标(o)和(h)分别代表输出层(out)和隐层(hide)，

例如，2输入，4隐节点，2输出的BP神经网络可以图解如下：

三. 三层BP神经网络梯度推导过程

本节我们具体推导误差函数对每一个待求参数w,b的梯度

3.1 简化推导目标

由于E的表达式较为复杂，

不妨先将问题转化为"求单样本梯度"来简化推导表达式
对于任何一个需要求偏导的待求参数w,都有:

$\displaystyle \dfrac{\partial \textbf{E}}{\partial w} = \dfrac{\partial \dfrac{1}{M}\sum \limits _{m=1}^{M} \dfrac{1}{K}\sum \limits _{k=1}^{K} (\textbf{f}(\textbf{x})_{km}-\text{y}_{km})^2 }{\partial w} =\dfrac{1}{M}\sum \limits _{m=1}^{M}\dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_{km}-\text{y}_{km})^2 }{\partial w} = \dfrac{1}{M}\sum \limits _{m=1}^{M}\dfrac{\partial \textbf{E}_m}{\partial w}$

即损失函数的梯度，等于单个样本的损失函数的梯度之和（E对b的梯度也如此），

因此，我们先推导单个样本的梯度，最后再对单样本梯度求和即可。

现在问题简化为求

$\dfrac{\partial\textbf{ E}_m}{\partial w} = \dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})^2 }{\partial w}$

3.2 输出层权重的梯度推导

输出层权重梯度推导
输出层的权重为"输出个数*隐节点个数"的矩阵,

现推导任意一个权重wji (即连接第i个隐层与第j个输出的权重)的单样本梯度

如下：

$\displaystyle \begin{aligned} \dfrac{\partial\textbf{ E}_m}{\partial w_\textbf{ji}^{(o)}} &= \dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_\textbf{k}-\text{y}_\textbf{k})^2 }{\partial w_\textbf{ji}^{(o)}} \\&= \dfrac{1}{K}\sum \limits _{k=1}^{K}\dfrac{\partial (\textbf{f}(\textbf{x})_\textbf{k}-\text{y}_\textbf{k})^2 }{\partial w_\textbf{ji}^{(o)}} \\&= \dfrac{1}{K}\sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_\textbf{k}-\text{y}_\textbf{k})\dfrac{\partial \textbf{f}(\textbf{x})_\textbf{k} }{\partial w_\textbf{ji}^{(o)}} \end{aligned}$
事实上，只有第j个输出
$\textbf{f(x)}_\textbf{j}$ 是关于
$w_\textbf{ji}^{(o)}$ 的函数，也即对于其它输出
$\dfrac{\partial \textbf{f}(\textbf{x})_{k(k\ne j )} }{\partial W} = 0$
因此，

上式即等于
$= \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \textbf{f}(\textbf{x})_\textbf{j} }{\partial w_\textbf{ji}}$

继续求导

$\displaystyle \begin{aligned} & \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \textbf{f}(\textbf{x})_\textbf{j} }{\partial w_\textbf{ji}^{(o)}} \\=& \color{blue}\dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \left ( w_\textbf{j1}^{(o)}*\textbf{tansig}_\textbf{1}+...+w_\textbf{ji}^{(o)}*\textbf{tansig}_\textbf{i}+...+w_\textbf{jh}^{(o)}*\textbf{tansig}_\textbf{h}+b_\textbf{j}^{(o)} \right ) }{\partial w_\textbf{ji}^{(o)}} \\= &\dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})*\textbf{tansig}_\textbf{i} \end{aligned}$
$\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j}$ 是第j个输出的误差，简记为
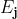
$E_\textbf{j}$

$\textbf{tansig}_\textbf{i}$ 是第j个隐节点的激活值，简记为
$A_\textbf{i}$ （A即Active）

上式即可写为

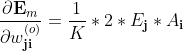
$\dfrac{\partial \textbf{E}_m}{\partial w_\textbf{ji}^{(o)}} = \dfrac{1}{K}* 2 *E_\textbf{j}*A_\textbf{i}$

**上述是单样本的梯度，
整体样本的梯度则应记为 **
$\displaystyle \dfrac{\partial \textbf{E}}{w_\textbf{ij}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} 2 *E_\textbf{jm}*A_\textbf{im}$

M,K为样本个数、输出个数

$E_\textbf{jm}=\textbf{f}(\textbf{x})_\textbf{jm}-\text{y}_\textbf{jm}$ 是第m个样本第j个输出的误差

$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值

3.3 输出层阈值的梯度推导

输出层阈值梯度推导
对于阈值
$b_\textbf{j}^{(o)}$ (第j个输出节点的阈值)的推导与权重梯度的推导是类似的，

只是上述标蓝部分应改为

$\displaystyle \begin{aligned} \dfrac{\partial \textbf{E}_{m} }{\partial b_\textbf {j}^{(o)}} &= \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \left ( w_\textbf{j1}^{(o)}*\textbf{tansig}_\textbf{1}+...+w_\textbf{ji}^{(o)}*\textbf{tansig}_\textbf{i}+...+w_\textbf{jh}^{(o)}*\textbf{tansig}_\textbf{h}+b_\textbf{j}^{(o)} \right ) }{\partial b_\textbf{j}^{(o)}} \\&= \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j}) \end{aligned}$
简记为

$\dfrac{\partial \textbf{E}_m}{\partial b_\textbf{j}^{(o)}} =\dfrac{1}{K}* 2 *E_\textbf{j}$

**上述是单样本的梯度，
整体样本的梯度则应记为 **
$\dfrac{\partial \textbf{E}}{\partial b_\textbf{j}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M}* 2 *E_\textbf{jm}$
M,K为样本个数、输出个数

$E_\textbf{jm}=\textbf{f}(\textbf{x})_\textbf{jm}-\text{y}_\textbf{jm}$ 是第m个样本第j个输出的误差

3.4隐层权重的梯度推导****

隐层的权重为"隐节点个数*输入个数"的矩阵,

现推导任意一个权重
$w_\textbf{ji}^{(h)}$ (即连接第i个输入与第j个隐节点的权重)的单样本梯度

如下：

$\displaystyle \begin{aligned} \dfrac{\partial\textbf{ E}_m}{\partial w_\textbf{ji}^{(h)}} &= \dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})^2 }{\partial w_\textbf{ji}^{(h)}} \\&= \dfrac{1}{K} \sum \limits _{k=1}^{K}\dfrac{\partial (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})^2 }{\partial w_\textbf{ji}^{(h)}} \\&= \dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \textbf{f}(\textbf{x})_{k} }{\partial w_\textbf{ji}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \left ( w_\textbf{k1}^{(o)}*\textbf{tansig}_\textbf{1}+...w_\textbf{kj}^{(o)}*\textbf{tansig}_\textbf{j}+...+w_\textbf{kh}^{(o)}*\textbf{tansig}_\textbf{h}+b_\textbf{k}^{(o)} \right ) }{\partial w_\textbf{ji}^{(h)}} \end{aligned}$

只有第j个tansig是关于
$w_\textbf{ji}^{(h)}$ 的函数，所以上式可以写成

$=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \left ( w_\textbf{kj}^{(o)}*\textbf{tansig}_\textbf{j} \right ) }{\partial w_\textbf{ji}^{(h)}}$

继续求导

$\displaystyle \begin{aligned} &=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \left ( w_\textbf{kj}^{(o)}*\textbf{tansig}_\textbf{j} \right ) }{\partial w_\textbf{ji}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left ( \textbf{tansig}_\textbf{j} \right ) }{\partial w_\textbf{ji}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial w_\textbf{ji}^{(h)}} \end{aligned}$
$\color{blue}=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }\dfrac{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }{\partial w_\textbf{ji}^{(h)}}$
$\displaystyle \begin{aligned} &=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }x_\textbf{i} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)}) \right ) }{\partial (\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)})}x_\textbf{i} \end{aligned}$

又由
$\textbf{tansig}'(x) = 1-\textbf{tansig}^2(x)$
所以上式为：

$\dfrac{\partial \textbf{E}_m }{\partial w_\textbf{ji}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}* \left (1-\textbf{tansig}_\textbf{j}^2\right ) x_\textbf{i}$
简写为

$\displaystyle \dfrac{\partial \textbf{E}_m }{\partial w_\textbf{ji}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *E_k*w_\textbf{kj}^{(o)}* \left (1-A_\textbf{j}^2\right ) x_\textbf{i}$

上述是单样本的梯度，对整体样本则有：

$\displaystyle \dfrac{\partial \textbf{E} }{\partial w_\textbf{ji}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right ) x_\textbf{im}$
M,KM,K为样本个数、输出个数

$E_\textbf{km}=\textbf{f}(\textbf{x})_\textbf{km}-\text{y}_\textbf{km}$ 是第m个样本第k个输出的误差

$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值

$x_\textbf{im}$ 是第m个样本第i个输入

3.5 隐层阈值的梯度推导

隐层阈值梯度推导
对于阈值b_\textbf{j}^{(h)} (第j个隐节点的阈值)的推导与隐层权重梯度的推导是类似的，

只是蓝色部分应改为

$\displaystyle \begin{aligned} &=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }\dfrac{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }{\partial b_\textbf{j}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)}) \right ) }{\partial (\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)}) } \end{aligned}$

又由
$\textbf{tansig}'(x) = 1-\textbf{tansig}^2(x)$
所以上式为：

$\dfrac{\partial \textbf{E}_m }{\partial b_\textbf{j}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}* \left (1-\textbf{tansig}_\textbf{j}^2\right )$
简写为
$\displaystyle \dfrac{\partial \textbf{E}_m }{\partial b_\textbf{j}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *E_k*w_\textbf{kj}^{(o)}* \left (1-A_\textbf{j}^2\right )$

上述是单样本的梯度，对整体样本则有：

$\displaystyle \dfrac{\partial \textbf{E} }{\partial b_\textbf{j}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right )$
M,K为样本个数、输出个数

$E_\textbf{km}=\textbf{f}(\textbf{x})_\textbf{km}-\text{y}_\textbf{km}$ 是第m个样本第k个输出的误差

$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值

四. 推导结果总结

4.1 三层BP神经网络梯度公式

输出层梯度公式
输出层权重梯度：
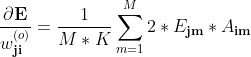
$\displaystyle \dfrac{\partial \textbf{E}}{w_\textbf{ji}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} 2 *E_\textbf{jm}*A_\textbf{im}$

输出层阈值梯度：
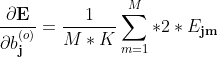
** ** $\displaystyle \dfrac{\partial \textbf{E}}{\partial b_\textbf{j}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M}* 2 *E_\textbf{jm}$

隐层梯度公式
隐层权重梯度：
$\displaystyle \dfrac{\partial \textbf{E} }{\partial w_\textbf{ji}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right ) x_\textbf{im}$
隐层阈值梯度：
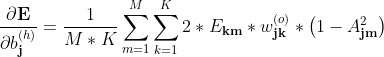
** ** $\displaystyle \dfrac{\partial \textbf{E} }{\partial b_\textbf{j}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right )$

✍️符号说明
M,K为样本个数、输出个数

$E_\textbf{km}=\textbf{f}(\textbf{x})_\textbf{km}-\text{y}_\textbf{km}$ 是第m个样本第k个输出的误差

$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值

$x_\textbf{im}$ 是第m个样本第i个输入

** 相关文章**

《BP神经网络梯度推导》

《BP神经网络提取的数学表达式》

《一个BP的完整建模流程》

标签：算法人工智能

本文转载自: https://blog.csdn.net/dbat2015/article/details/128091135
版权归原作者 老饼讲解-BP神经网络 所有，如有侵权，请联系我们删除。

BP神经网络的梯度公式推导(三层结构)

一. 推导目标

1.1 梯度公式目标

1.2 本文梯度公式目标

二. 网络表达式梳理

2.1 梳理三层BP神经网络的网络表达式

三. 三层BP神经网络梯度推导过程

3.1 简化推导目标

3.2 输出层权重的梯度推导

3.3 输出层阈值的梯度推导

3.4隐层权重的梯度推导****

3.5 隐层阈值的梯度推导

四. 推导结果总结

4.1 三层BP神经网络梯度公式

发表评论

“BP神经网络的梯度公式推导(三层结构)”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航

BP神经网络的梯度公式推导(三层结构)

一. 推导目标

**1.1 梯度公式目标 **

1.2 本文梯度公式目标

二. 网络表达式梳理

2.1 梳理三层BP神经网络的网络表达式

三. 三层BP神经网络梯度推导过程

3.1 简化推导目标

3.2 输出层权重的梯度推导

3.3 输出层阈值的梯度推导

3.4隐层权重的梯度推导****

3.5 隐层阈值的梯度推导

四. 推导结果总结

4.1 三层BP神经网络梯度公式

发表评论

“BP神经网络的梯度公式推导(三层结构)”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航

1.1 梯度公式目标