Easy Deep Learning——卷积层

为什么需要卷积层，深度学习中的卷积是什么？

在介绍卷积之前，先引入一个场景

假设您在草地上漫步，手里拿着一个尺子，想要测量草地上某些物体的大小，比如一片叶子。但是叶子的形状各异，并且草地非常大，您要用一款尺子轻易地测量出草地上所有叶子的大小。

显然，这很难做到，那么引入卷积的概念

于是，您想到了一种方法，即将叶子放在一个网格纸上，并把网格纸放在尺子上。您现在只需要记录纸张上每个网格的大小，然后用它们来计算叶子的大小。

在深度学习中，直接输入原始数据是可行的，但是如果数据的尺寸很大，比如图像、音频或视频等，那么会遇到以下问题：

1. 参数数量过多：如果直接将大型图像输入神经网络，由于图像的尺寸可能很大，因此网络的参数数量也会相应增加。这将导致更多的计算量和更多的内存需求。而卷积操作可以共享参数，通过卷积核对输入数据进行特征提取，从而减少了需要训练的参数数量，降低了计算量和内存需求。
2. 局部相关性：对于大型图像，其中的信息通常是局部相关的。也就是说，相邻的像素通常具有相似的特征。卷积操作通过滑动窗口对输入数据进行卷积操作，可以有效地捕捉局部相关性，从而提高模型的精度。
3. 平移不变性：图像的很多特征（如边缘、纹理等）在不同位置都是具有相似性质的。卷积操作具有平移不变性，也就是说，无论特征出现在图像的哪个位置，卷积操作都能够将其检测出来。这种平移不变性对于图像识别、物体检测等任务非常重要。

卷积是一种数学运算，用于在信号处理和图像处理中的滤波器操作中，也是卷积神经网络中重要的计算操作。卷积运算的目的是将一个函数（比如图像）与另一个函数（比如卷积核）做积分，从而得到新的函数，实现信号的去噪、特征提取、图像增强等操作。在卷积神经网络中，卷积操作是通过卷积层实现的，可以提取出图像中的特征信息，帮助神经网络更好地学习和分类。

卷积层作为深度学习中的重要组成部分，可以有效地减少参数数量，提高模型的精度，并且具有平移不变性和捕捉局部相关性的优势，因此被广泛应用于图像、音频、视频等数据的处理和分析中。

回到最初的场景中，网格纸就像是一个卷积核，它可以帮助您捕捉叶子的特征并将其转换为数字数据。同样，深度学习中的卷积也是这个原理，它将输入的数据通过卷积核的滑动操作，将每一部分的特征转化为数字数据，进而进行后续的处理和分析。

下面引入卷积对图像的数据处理为例，介绍Pytorch中卷积运行的实现。

图像的卷积计算案例——conv2d

torch.nn模块包含着torch已经准备好的层，方便使用者调用构建网络。

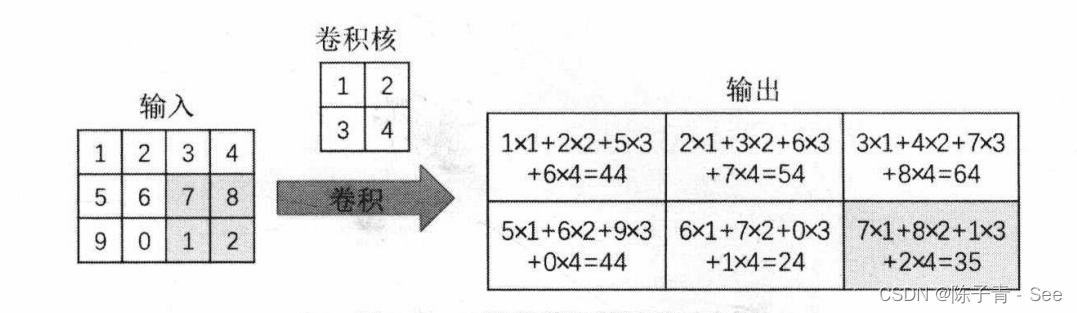
案例:[1]

上图是一个二维卷积运算的示例，可以发现，卷积操作将周围几个像素的取值经过计算得到一个像素值。

---

使用卷积运算在图像识别、图像分割、图像重建等应用中有三个好处，即卷积稀疏连接、参数共享、等变表示，正是这些好处让卷积神经网络在图像处理算法中脱颖而出。
在卷积神经网络中，通过输人卷积核来进行卷积操作，使输入单元(图像或特征映射)和输出单元(特征映射)之间的连接是稀疏的，这样能够减少需要训练参数的数量，从而加快网络的计算速度
卷积操作的参数共享特点，主要体现在模型中同一组参数可以被多个函数或操作共同使用。在卷积神经网络中，针对不同的输人会利用同样的卷积核来获得相应的输出。这种参数共享的特点是只需要训练一个参数集，而不需对每个位置学习一个参数集合。由于卷积核尺寸可以远远小于输入尺寸，即减少需要学习的参数的数量，并且针对每个卷积层可以使用多个卷积核获取输入的特征映射，对数据(尤其是图像)具有很强的特征提取和表示能力，并且在卷积运算之后，使得卷积神经网络结构对输入的图像具有平移不变的性质。

---

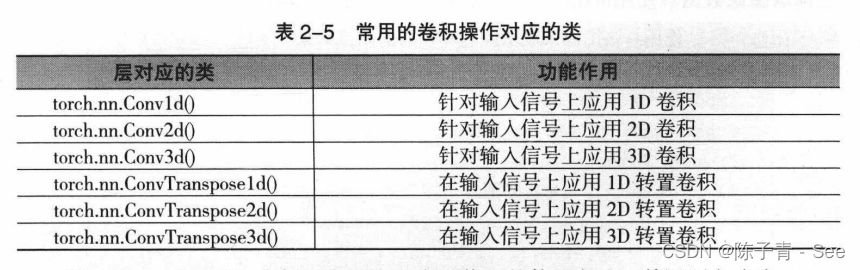
在PyTorch中针对卷积操作的对象和使用的场景不同，有一维卷积、二维卷积三维卷积与转置卷积(可以简单理解为卷积操作的逆操作)，但它们的使用方法比较相似，都可以从torch.nn模块中调用，需要调用的类如表所示。

针对一张图像，经过二维卷积后的输出会是什么样子呢?下面使用一张图像来展示经过卷积后，输出的特征映射的结果。先导入相关的包和模块，并且使用PIL包读取图像数据，使用matplotlib包来可视化图像和卷积后的结果，程序如下:

import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from PIL import Image

# 读取图像并将其转换为灰度图
img = Image.open("/home/cbc/图片/2.png")
imgGray =np.array(img.convert("L"),dtype=np.float32) #convert("L") 转换为单通道图片

# 绘制灰度图
plt.figure(figsize=(6,6))
plt.imshow(imgGray,cmap=plt.cm.gray)
plt.axis(False) #禁用坐标轴显示
plt.show()

经过上述操作之后，得到一个二维数组，在使用PyTorch进行卷积操作之前，需要将其转化为1×1×高×宽的张量。

将二维的灰度图像转换成四维的张量，维度为(1, 1, imh, imw)，表示一个batch（案例数），一个通道，高为imh，宽为imw

imh,imw = imgGray.shape
# 将二维的灰度图像转换成四维的张量，维度为(1, 1, imh, imw)，表示一个batch，一个通道，高为imh，宽为imw
imgGray_torch = torch.from_numpy(imgGray.reshape((1,1,imh,imw)))
print(imgGray_torch.shape)

卷积时需要将图像转化为四维来表示[batch,channel,h,w ]。在对图像进行卷积操作后，获得两个特征映射。第一个特征映射使用图像轮廓提取卷积核获取，第二个特征映射使用的卷积核为随机数，卷积核大小为5×5,对图像的边缘不使用0填充。

卷积核中心值为 24，其余为 -1，这种卷积核叫做边缘检测算子。在卷积操作中，卷积核与图像中每个像素的值进行乘积并求和，得到的结果就是该像素的卷积值。

对于边缘检测算子，它会在图像中找到像素值变化最为明显的地方，也就是图像中的边缘部分，因为边缘处的像素值变化较为剧烈。通过卷积操作，边缘部分的卷积值会比其他部分更高，从而实现提取图像轮廓的效果。

对卷积后的两个特征映射进行可视化：

# 定义卷积核大小和卷积核矩阵，其中心为24，其余为-1
kersize = 5
ker = torch.ones(kersize,kersize,dtype=torch.float32) *-1
ker[2,2] =24
ker = ker.reshape((1,1,kersize,kersize))

# 将卷积核矩阵转换成张量，维度为(1, 1, kersize, kersize)，表示一个batch，一个通道，卷积核的高和宽分别为kersize
ker = ker.reshape((1,1,kersize,kersize))

# 定义一个2D卷积层，输入通道数为1，输出通道数为2，卷积核的大小为(kersize,kersize)，不使用偏置项
conv2d = nn.Conv2d(1,2,(kersize,kersize),bias= False)

# 将卷积核张量赋值给卷积层的权重，第一个通道的权重为ker
conv2d.weight.data[0] = ker

# 对灰度图像进行卷积操作
imconv2dout = conv2d(imgGray_torch)

# 将卷积结果的张量降维成二维数组
imconv2dout_im = imconv2dout.data.squeeze()

# 打印卷积结果的形状
print("卷积后的尺寸:",imconv2dout_im.shape)

# 绘制卷积结果的两个通道
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(imconv2dout_im[0],cmap=plt.cm.gray)
plt.axis(False)
plt.subplot(1,2,2)
plt.imshow(imconv2dout_im[1],cmap=plt.cm.gray)
plt.axis(False)
plt.show()

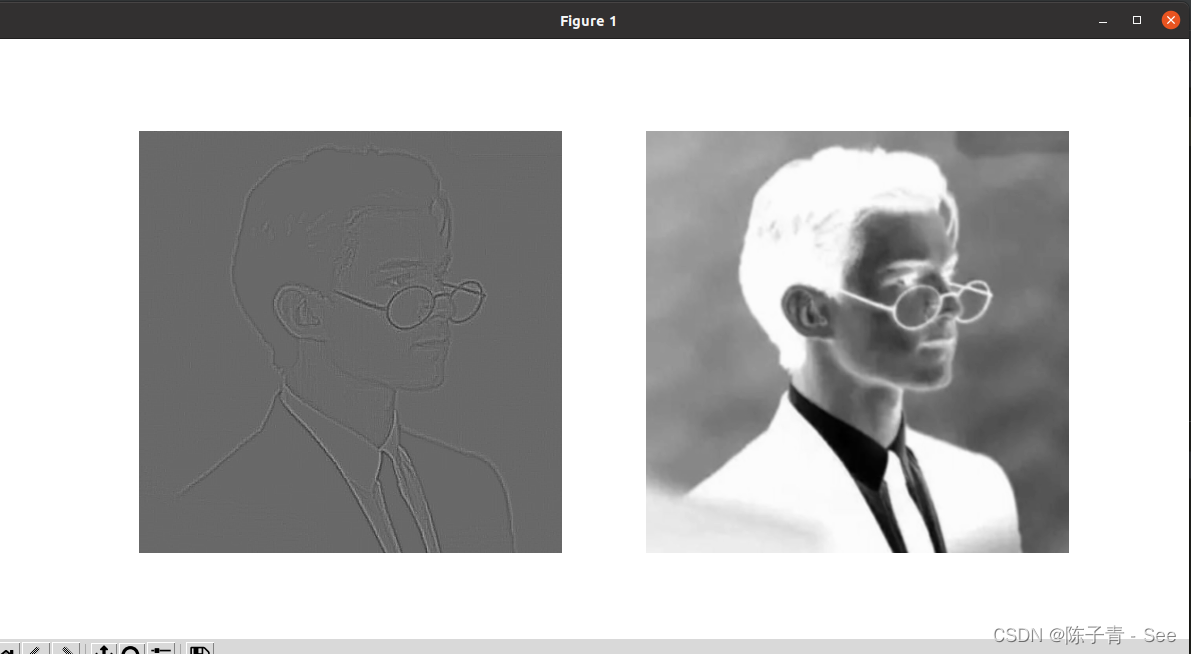
可以看出，使用的边缘特征提取卷积核很好地提取出了图像的边缘信息。而右边的图像使用的卷积核为随机数，得到的卷积结果与原始图像很相似。

• [1]《PyTorch 深度学习入门与实战（案例视频精讲）》，孙玉林，余本国*