摘要及声明
1:本文主要介绍Grinold Kroner(GK)模型的运用,并以上证指数为例实现一个GK模型;
2:本文主要为理念的讲解,模型也是笔者自建,文中假设与观点是基于笔者对模型及数据的一孔之见,若有不同见解欢迎随时留言交流;
3:笔者希望搭建出一套交易体系,原则是只做干货的分享。后续将更新更多内容,但工作学习之余的闲暇时间有限,更新速度慢还请谅解;
4:本文主要数据通过Tushare(ID:444829)金融大数据平台接口获取;
5:模型实现基于python3.8;
很多分析师计算股票市场的总体回报率通常利用某个指数的历史数据进行计算,但这样的纯数理统计做法缺少了经济意义的解释。本期笔者将介绍一个蕴含有**更深刻经济学意义**的股票市场回报率计算方法——Grinold Kroner模型(下文简称**“GK模型”****)**,本文主要内容如下:
1. 市场回报率的估计方式
关于回报率笔者已经在本专栏往期的内容中有过很详细的介绍,但之前所计算的回报率是单个证券的回报率。**本期所谈的回报率是对于市场总体而言的回报率**,也可以简单理解成将构建一个包含所有证券的投资组合,这个投资组合的收益率即是市场回报率。既然要囊括所有的证券,比较有代表性的指数就成了很好的替代品。
由于二级市场数据的公开和可得性,计算市场回报率变成一种非常简单粗暴的方法:用指数历史数据算年化回报。当然,计算和年化的方式多种多样,以上证指数2013年1月4日到2022年12月31日数据为例:
df = pro.index_daily(ts_code='000001.SH', start_date='20130101', end_date='20221231')
1):用期间价格收益率再进行年化可得市场回报率:3.10%
start = df["close"][df["trade_date"]=="20130104"].values[0]
end = df["close"][df["trade_date"]=="20221230"].values[0]
print("Market return(%):", ((1 + (end - start) / start)**(1/10) - 1) * 100)
# Market return(%): 3.097769
2):用平均日回报再进行250个交易日年化可得市场回报率:5.53%
print("Market return(%):",((1 + df["pct_chg"].mean() / 100) ** 250 - 1) * 100)
# Market return(%): 5.533287
其实这里已经能看出采用历史数据计算市场回报率的弊端了。首先是统计区间,市场是时时刻刻在波动的,如果笔者选取的统计区间是2008年指数高点到现在的数据,回报率计算出来毫无疑问是个负数。这种180度的变化从根源上讲是由于数据的不稳定性导致的,而**对于不稳定的数据用过去的历史代表未来是十分不可靠的**。
图一:上证指数2013年至2022年走势
另外,**不同的计算方法也直接导致计算出的数据大相径庭**。之前的例子中,平均日年化回报超过了价格收益率79% (5.53-3.10)/3.10,这是相当大的差距。最后,通过这种历史数据计算的市场收益率**缺乏相应的经济含义**,很难说清楚它的来源、组成部分或者由哪些因子贡献。
不过由于数据的可得性和简单明了,实务中依然有大量的专业从业人员使用这种方法。这反而也成了这种方法的优势——比较为业内所接受。但是,笔者本着勤勉尽责的态度所追求的是合理性和经济意义,这种傻瓜方式已经难以满足笔者的需要。
2. GK模型
GK模型是理查德格林诺德(Richard Grinold)和肯尼思克罗钠(Kenneth Kroner)共同提出的理论【1】,网上其实有一些文章写过该模型,但很多都是停留在公式层面的解释,不够深刻。下面谈的GK模型虽然是基于Grinold和Kroner的论文,但更多是笔者自己的理解和推导,有想看原论文的可以通过文末参考文献的链接下载。
2.1 从戈登增长到GK模型
折现率在戈登增长模型中扮演一个重要角色,如果将折现率独立出来,戈登增长模型可以写成:
其中,是股利的增速,同时也是股票股价(内在价值)的增速。
不过用这个式子的目的不是回测过去的回报率,主要目的还是预测未来,因此在外面套上个预期,得到[1]式:
其实这个式子就已经具有一定的的经济含义了:预期回报率可以拆解为股息率和股利增速两个部分。由于同时也是股价的增速,实际上就是买卖股票的资本利得。因此,**这个式子也可以将股票收益解释为股利和资本利得两个来源**。
但是笔者依旧不满足,股利还很好说,但资本利得里面的门道就大了去了,如何计量出来还要有经济意义又是一件考验功夫的活儿。Grinold和Kroner就提出一个解决思路,原理其实和杜邦拆解一样。**下面是笔者自己的推导,和原论文的过程不太一样,但结果和原理是一致的**。
由于资本利得就是股价的变化,因此可以先将股价拓展成下面的等式:

其中:P为股价,EPS为每股收益。
EPS还可以进一步用净利润除以发行股数展开,得到[2]式:
有这个式子就很好办了,由于的定义是股价的变化,只要在[2]式两边同时取对数即可转化为变化量:
[3]式差分一下改写为变化量,就是PE指标,于是有[4]式:
![g = %\Delta P = %\Delta Earnings-%\Delta No. \, \, of \, \, shares +%\Delta PE\, \, \, [4]](https://latex.csdn.net/eq?%5Cinline%20g%20%3D%20%25%5CDelta%20P%20%3D%20%25%5CDelta%20Earnings-%25%5CDelta%20No.%20%5C%2C%20%5C%2C%20of%20%5C%2C%20%5C%2C%20shares%20+%25%5CDelta%20PE%5C%2C%20%5C%2C%20%5C%2C%20%5B4%5D)
将[4]合并进戈登增长模型,得到[5]式:
**这个[5]式其实就是GK模型**,笔者认为自己的这个推导方式比原论文的更简洁明了一些。一个需要注意的点是原论文中第五步的推导将原来用得好好的等号变成了约等号,如图二:
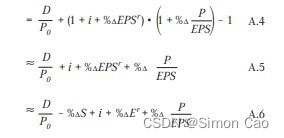
图二:GK模型推导(原论文截图)
原论文作者在这个地方用约等于其实是基于谨慎性的考虑,因为该模型还是有一些成立条件的。笔者认为加不加都行,对结果影响不大。
2.2 从GK模型看投资的本质
下面笔者对拆解的式子进行简要分析。
,这个两个部分相加称为**预期现金回报**(Expected cash flow return或Expected income return)。顾名思义,即是实实在在可以拿到手中(Bird in hand)的钱。因为股票数量的变化是减项,因此公司发行新股会降低预期回报率,而回购股票会增加预期回报率(关于回购增发对股价的影响可以参考信号理论,这里就不展开了)。
,**预期名义利润增速回报**(Expected nominal earnings growth return)。这块回报率是名义上的,要考虑通胀因素。
,**预期市场重定价回报**(Expected repricing return)。PE指标的预期变化率,不过有的文献也直接叫做PE指标变化率。
当然,以上指标还有其它的理解方式,例如:
,这两块合起来看其实就是EPS的增长率。
,这两块其实就是大名鼎鼎的戴维斯双击。
GK模型的精义之处其实就是对预期回报率的拆解,它很清楚的从经济意义上告诉投资者收益的来源。在市场上进行交易就一定要想明白一个问题:你赚的是谁的钱?笔者相信有很多从事交易的人会说股票的供求关系,会说股价上涨的原理,会把市场上的玩家们罗列一通然后得出结论散户在食物链的最底层是被割得最惨的。但这个资金的逻辑链不是一个基本面投资者的世界观。
GK模型对赚谁的钱这个问题提供了基本面上的解释,即**回报的来源主要由预期现金回报,利润增速回报和市场定价回报这几个部分组成。**其中预期现金回报,利润增速回报的来源于公司,所**赚的是公司成长的钱**。市场定价回报来源于市场给予公司的估值水平,**赚的是市场定价的钱**。把这两个部分进一步拆分来看,上市公司分红和增发回购不是任何投资者都能参与的,且像增发回购有着非常大的不确定性。因此预期现金回报率对于普通投资者来说是难以控制的因素。而利润增速回报和市场定价回报这两块则是投资者可以通过完善的研究方法实现的。**即找到未来高利润率,市场还愿意给予高估值的公司,这是基本面投资的本质**。
不过笔者还想提醒一点,在网上搜一搜戴维斯双击,度娘给出的解释是“在低市盈率(PE)买入股票,待成长潜力显现后,以高市盈率卖出的投资策略”,还有一大堆的文章,但重点都在于”低市盈率“,或者说“低估”这些字眼上。笔者认为,所谓**戴维斯双击其最重要的不在于其现在很“低”,而是在于未来要能“高”得起来。**例如中国神车,例如中国神油,还有一大堆的破净银行和钢铁,它们都是低的公司。很多公司低了以后几十年都再也高不上去了,公司未来要高的**核心在于Earnings,在于其基本面**,有这些做为支撑,未来才有可能做大做强,再创辉煌。
3. 模型实现
在理解原理后就可以将模型实现出来了,笔者的目标是利用GK模型计算出上证指数2010年至今的市场回报率。需要注意的是GK模型所使用的数据应该都是预期值,由于预期数据是个仁者见仁智者见智的过程,很难说有什么统一的标准。因此,笔者下面所展示的更多是是当下和历史的市场回报率的计算。
由于需要处理2千多家公司十几年的数据,使用电子表格(EXCEL)显然是非常困难的事情,因此还是需要通过代码实现,并且还可以将代码封装成模块嵌入其它模型中,极大的降低了数据处理的难度。
3.1 数据获取与准备
笔者使用Tushare金融大数据平台接口请求数据(Tushare数据),花几分钟时间注册即可使用自己的密钥请求数据,非常方便。下面导入需要的模块,实例化数据接口:
import pandas as pd
import tushare as ts
import numpy as np
pro = ts.pro_api("token") # 输入自己的密钥
首先拿到上证指数所有公司的列表,共2176家公司(包含已退市公司):
stocks = pro.stock_basic(exchange='SSE', list_status='', fields='ts_code')["ts_code"].values
print(len(stocks))
# 2176
根据GK模型公式,笔者需要的数据有上市公司股息率、总股本、净利润和PE指标,指数PE指标后面可以通过Tushare接口至今请求到,不用额外计算。多请求一个总市值,方便后面进行市值加权平均。财务数据是有一定滞后的,多请求一年:
# 总市值,股本,股息率
daily_indicators = pro.daily_basic(ts_code=code, start_date='20100101', end_date='20230215', fields='ts_code,trade_date,total_mv,total_share,dv_ratio')[::-1]
# 净利润
financial = pro.income(ts_code=code, start_date='20090101', end_date='20230215', fields='ts_code,ann_date,n_income')[::-1]
可以看到,市场数据和财务数据是分开请求的,因此接下来的难点在于将财务数据合并进市场数据。将表格索引设置为日期,按日期进行合并即可,但是这里需要注意财务数据公布时间点和财报数据截至时间点是不一样的。例如图三,2022年年报截至期是2022年最后一天,但实际能拿到数据是23年的4月份了:

图三:财报公布期的滞后性
因此,在财务数据中添加一个字段,添加下一个财报公告的日期:
financial["end_date"] = financial["ann_date"].shift(1)
这样只需要在交易数据中筛选符合报告日期区间的行数据,添加一个净利润字段即可,例如:
start = financial["ann_date"][0]
end = financial["end_date"][0]
selector = (daily_indicators["trade_date"]>start) & (daily_indicators["trade_date"]<=end)
daily_indicators.loc[selector, "n_income"] = financial["n_income"][i]
当然,上面的代码只能跑单个公司,将上面的代码封装成模块并美化一下:
def data_mod(code):
daily_indicators = pro.daily_basic(ts_code=code, start_date='20100101', end_date='20230215', fields='ts_code,trade_date,total_mv,total_share,dv_ratio')[::-1]
financial = pro.income(ts_code=code, start_date='20090101', end_date='20230215', fields='ts_code,ann_date,n_income')[::-1]
financial.drop_duplicates("ann_date", inplace=True)
financial["end_date"] = financial["ann_date"].shift(-1)
financial.loc[0,"end_date"] = "20230215" # 填充一个最新的日期
financial["n_income"] = financial["n_income"].rolling(4).sum() # 滚动年净利润
financial.dropna(inplace=True)
daily_indicators.fillna(0, inplace=True)
daily_indicators["n_income"] = None
for i in range(len(financial)):
start = financial["ann_date"][i]
end = financial["end_date"][i]
selector = (daily_indicators["trade_date"]>start) & (daily_indicators["trade_date"]<=end)
daily_indicators.loc[selector, "n_income"] = financial["n_income"][i]
return daily_indicators
循环遍历之前的公司列表,再写个进度展示:
tables = []
stocks = pro.stock_basic(exchange='SSE', list_status='', fields='ts_code')["ts_code"].values
for code in stocks:
table = data_mod(code)
tables.append(table)
# table.to_csv(code+".csv") # 保存本地
print("已完成(%):{}\r".format('%.2f'%(100*((1+list(stocks).index(code))/len(stocks)))), end="")
tables中就存储着所需要的所有公司数据。
3.2 回报率计算
先创建几个空表用来分别存储GK模型中的几个因子,PE可以先不用管,后面直接通过Tushare请求指数的PE数据即可。获取上证指数的交易数据,将其日期设置为空白表格的索引:
index = pro.index_daily(ts_code='000001.SH', start_date='20100101', end_date='20230215')
div_dataset = pd.DataFrame() # 股息率
num_share_dataset = pd.DataFrame() # 股本
earnings_dataset = pd.DataFrame() # 净利润
mv_dataset = pd.DataFrame() # 市值
div_dataset.index = index["trade_date"]
mv_dataset.index = index["trade_date"]
num_share_dataset.index = index["trade_date"]
earnings_dataset.index = index["trade_date"]
接下来将每个公司的大数据集拆分合并进各个因子的数据集中:
for i in range(len(tables)):
code = stocks[i]
table = tables[i]
table.index = table["trade_date"]
div_dataset = pd.concat([div_dataset,table["total_mv"]*(table["dv_ratio"]/100)], axis=1) # 股息率采用市值加权
num_share_dataset = pd.concat([num_share_dataset,table["total_share"]], axis=1)
earnings_dataset = pd.concat([earnings_dataset, table["n_income"]], axis=1)
mv_dataset = pd.concat([mv_dataset, table["total_mv"]], axis=1)
print("合并完成度:{}%\r".format("%.2f"% (100 * (i + 1) / len(tables))), end="")
按照GK模型公式,该转化为变化率的转化成变化率,该加的加,该减的减。另外将指数的PE指标也请求到,最后将所有数据合并进一个大表里:
# 修改列索引为证券代码
div_dataset.columns = stocks
mv_dataset.columns = stocks
num_share_dataset.columns = stocks
earnings_dataset.columns = stocks
# 加总,除以总市值计算市值加权
mv_dataset["sum_mv"] = mv_dataset.apply(lambda x: x.sum(), axis=1)
div_dataset["sum_div"] = div_dataset.apply(lambda x: x.sum(), axis=1)
div_dataset["avg_div"] = div_dataset["sum_div"] / mv_dataset["sum_mv"]
num_share_dataset["sum_shares"] = num_share_dataset.apply(lambda x: x.sum(), axis=1)
num_share_dataset["avg_shares"] = num_share_dataset["sum_shares"] / mv_dataset["sum_mv"]
earnings_dataset["sum_earnings"] = earnings_dataset.apply(lambda x: x.sum(), axis=1)
earnings_dataset["avg_earnings"] = earnings_dataset["sum_earnings"] / mv_dataset["sum_mv"]
# 创建总数据表
dataset = pd.DataFrame()
dataset.index = index["trade_date"][::-1]
# 配合移动年价格回报率平滑数据
dataset["div"] = div_dataset["avg_div"][::-1].rolling(250).mean()
num_share = (num_share_dataset["avg_shares"] - num_share_dataset["avg_shares"].shift(-250))/num_share_dataset["avg_shares"].shift(-250)
dataset["num_shares"] = num_share[::-1].rolling(250).mean()
earnings = (earnings_dataset["avg_earnings"] - earnings_dataset["avg_earnings"].shift(-250))/earnings_dataset["avg_earnings"].shift(-250)
dataset["earnings"] = earnings[::-1].rolling(250).mean()
# 请求指数PE数据
pe = pro.index_dailybasic(ts_code="000001.SH", start_date='20100101',end_date='20230215', fields='trade_date,pe')
pe.index = pe["trade_date"]
pe = (pe["pe"] - pe["pe"].shift(-250))/pe["pe"].shift(-250)
dataset["pe"] = pe[::-1].rolling(250).mean()
最后得到的dataset就存储着计算GK模型所需要的所有因子,由于采用了移动窗口计算,数据起始日期变成了2012年10月31日,共计算出2501个交易日数据:
dataset.dropna()
div num_shares earnings pe
trade_date
20121031 0.022483 0.074004 0.280766 -0.310723
20121101 0.022507 0.073680 0.280165 -0.309922
20121102 0.022530 0.073303 0.279486 -0.309201
20121105 0.022555 0.072950 0.278849 -0.308484
20121106 0.022580 0.072581 0.278188 -0.307798
... ... ... ... ...
20230209 0.022658 -0.019366 0.068904 -0.162510
20230210 0.022688 -0.019219 0.069306 -0.163292
20230213 0.022718 -0.019059 0.069739 -0.164086
20230214 0.022747 -0.019006 0.070064 -0.164720
20230215 0.022775 -0.018906 0.070454 -0.165320
2501 rows × 4 columns
按照公式加总一下:
market_r = dataset["div"] - dataset["num_shares"] + dataset["earnings"] + dataset["pe"]
print(market_r.dropna())
trade_date
20121031 -0.081478
20121101 -0.080929
20121102 -0.080488
20121105 -0.080031
20121106 -0.079611
...
20230209 -0.051582
20230210 -0.052079
20230213 -0.052570
20230214 -0.052904
20230215 -0.053185
Length: 2501, dtype: float64
3.3 可视化分析
可以先看GK模型几个因子的变化情况,展示到子图上:
import matplotlib.pyplot as plt
plt.subplot(2,2,1)
plt.plot(range(len(dataset.index)), dataset["div"], color="orange", label="div")
plt.legend()
plt.subplot(2,2,2)
plt.plot(range(len(dataset.index)), dataset["num_shares"], color="orange", label="No. shares")
plt.legend()
plt.subplot(2,2,3)
plt.plot(range(len(dataset.index)), dataset["earnings"], color="orange", label="earnings")
plt.legend()
plt.subplot(2,2,4)
plt.plot(range(len(dataset.index)), dataset["pe"], color="orange", label="PE")
plt.legend()
plt.subplots_adjust(left=None,bottom=None,right=None,top=None,wspace=0.2,hspace=0.2)
plt.show()
运行得图四:
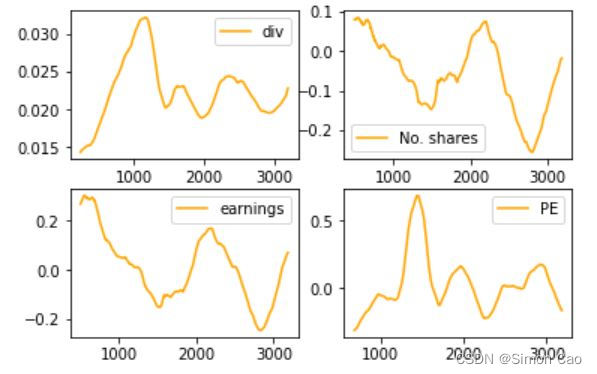
图四:GK模型四个因子历史走势
从走势上不难看出,股息率与PE走势相关性较高;净利润与发行股本数量相关性较高;而股息率及PE走势,和净利润及发行股本的走势呈现一定的负相关。首先股票数量和PE的关系很好理解,发行股数越多,会拉低EPS进而拉高PE指标,因此呈现负相关关系。同理,净利润越高EPS也越高,进而拉低PE指标,因此也呈现负相关关系。
比较难以理解的是净利润与股息率呈现出负相关关系,按理来说净利润越多,公司发放股利的能力越高,越有可能产生高股息率。这一现象可能争议比较大,笔者认为是股利政策的滞后性导致的错配。一个很明显的现象是净利润增长达到顶峰时往往不是分红的顶峰,很多公司在净利润率经历下降的阶段却依旧坚持高分红,笔者认为这种滞后性是导致负相关的直接原因。如果读者有不同见解也欢迎留言交流。
市场回报数据也可以输出到图表上:
market_r.plot(figsize=(16,5), color="orange", ylabel="return")
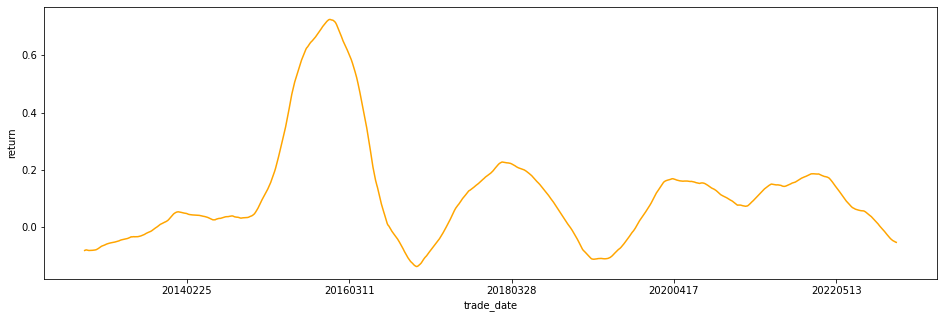
图五:上证收益率走势(GK模型)
查看一下均值,GK模型所得的历史平均回报率为11.56%:
market_r.mean()
# 0.11556596705632231
由于15年那波大牛市的极端影响,去掉收益率超过20%的数据再计算平均值,得**5.04%**。**笔者认为该数值从基本面上看很好的代表了上证指数长期的年化回报率**:
market_r[market_r<=0.2].mean()
# 0.05038140990666294
3.4 归因分析
与多因子模型原理类似,笔者希望找到GK模型对上证指数真实回报率的解释力度到底有多强。获取上证指数日线数据,一样计算250日移动年价格回报率, 最后可视化输出:
index = pro.index_daily(ts_code='000001.SH', start_date='20100101', end_date='20230215')
index.index = index["trade_date"]
r = (index["close"] - index["close"].shift(-250))/index["close"].shift(-250)
r = r[::-1]
r = r.rolling(250).mean()
plt.figure(figsize=(10,5))
plt.plot(market_r.index, market_r, label="GK_model", color="orange")
plt.plot(market_r.index, r, label="SH_history", color="blue")
plt.xlabel("trade date")
plt.ylabel("return(%)")
plt.xticks(market_r.index[::250], rotation=90)
plt.legend()
plt.show()
如图六展示的,GK模型所得到的结果与历史发走势是高度一致的,但是GK模型整体要高一点,所得到的均值上比历史真实回报要高上许多。
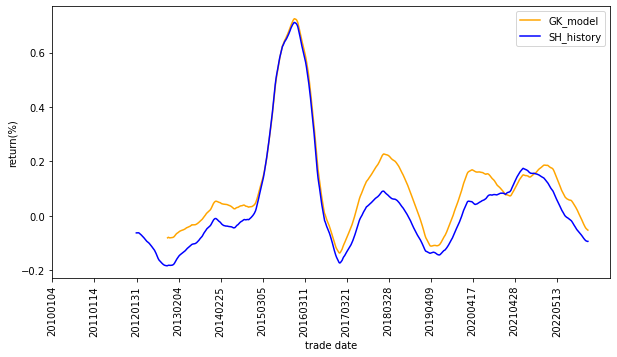
图六:GK模型与历史回报率对比
下面进行严谨的多因子分析,建立回归模型将结果输出。可以看到,模型解释力度达98%,四因子均有非常高的显著度。从因子系数上看敏感度最高的是股息率,而戴维斯双击的部分敏感度较低:
import statsmodels.formula.api as smf
dataset["index_history"] = r
reg = smf.gls(formula='index_history~div+num_shares+earnings+pe', data=dataset.dropna())
reg_result = reg.fit()
print(reg_result.summary())
GLS Regression Results
==============================================================================
Dep. Variable: index_history R-squared: 0.978
Model: GLS Adj. R-squared: 0.978
Method: Least Squares F-statistic: 2.826e+04
Date: Thu, 16 Feb 2023 Prob (F-statistic): 0.00
Time: 02:12:49 Log-Likelihood: 5239.9
No. Observations: 2501 AIC: -1.047e+04
Df Residuals: 2496 BIC: -1.044e+04
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.1638 0.004 -37.426 0.000 -0.172 -0.155
div 5.2286 0.186 28.036 0.000 4.863 5.594
num_shares -1.0752 0.018 -60.663 0.000 -1.110 -1.040
earnings 0.8026 0.014 58.850 0.000 0.776 0.829
pe 1.0091 0.004 282.086 0.000 1.002 1.016
==============================================================================
Omnibus: 229.001 Durbin-Watson: 0.000
Prob(Omnibus): 0.000 Jarque-Bera (JB): 72.005
Skew: -0.075 Prob(JB): 2.31e-16
Kurtosis: 2.183 Cond. No. 314.
==============================================================================
4. 总结
笔者认为GK模型相比起历史回报率,或者多因子模型中抽象的因子回报率来说具有更为正统的基本面色彩和经济意义。但是这个模型依旧是有缺陷的,看推导过程就不难发现它最根本的来源是戈登增长模型,GK模型无非是在GGM的基础上进一步对增速进行拆解。因此,**它也和GGM一样有着永续经营和永续增长的假设**。**但事实上拆解出来的一些项目是很难预期永续增长的**,例如,估值的均值回归效应会使得长期的市盈率变化为0,而GK模型中如果计算出市盈率变化是大于0的数,哪怕是市盈率按1%永续的增长到无穷期都不是一个能完全说服笔者的条件。
其次,从GK模型拆解出的几项不难看出,**它是对未来的预期,很多时候不能用历史数据外推**。预期是个仁者见仁智者见智的过程,这个东西就很难量化出来了。另外,是否还有更好的方式对资本利得进行拆解也有待研究。最后,正如之前笔者所言,市场上所广泛使用的依旧是历史估计未来,**GK模型无疑是一种非常小众的方式**,如果硬要将该模型嵌入传统的估值模型还需要考虑是不是能被市场所接受。
除了GK模型外,还有一个Singer Terhaar(ST)模型也可以计算预期市场回报率。ST模型的逻辑和GK模型完全不同,后面如果有时间再出一期介绍ST模型的文章。您若不弃,我们风雨共济。
5. 往期精选
往期精选系列文章传送门****实现方式基本面分析实现GGM的理想国PythonPB指标与剩余收益估值PythonFama-French及PSMPythonGrinold Kroner(GK)模型(本期)Python增速g的测算PythonPE指标平滑PythonPE BandPython技术分析分类树算法R蒙特卡洛模拟Python全连接神经网络模型Python组合管理券商金股哪家强——信息比率Python从指数构建原理看待A股的三千点魔咒Python决策树学习基金持仓并识别公司风格类型R杂谈类垃圾公司对回报率计算的影响几何Python市场风险分析Python金融危机模拟Python
6. 参考文献
【1】:Grinold, R. & Kroner, K. 2002. "The equity risk premium——Analyzing the long-run prospects for the stock market". Investment Insights. 5(3). 1-33. https://silo.tips/download/the-equity-risk-premium-by-richard-grinold-and-kenneth-kroner
版权归原作者 Simon Cao 所有, 如有侵权,请联系我们删除。