本文主要基于《Handbook of Fingerprint Recognition》第三版第三章“Fingerprint Analysis and Representation”的内容。本文会不定期更新,以反映一些新的进展和思考。
1、引言
利用指纹采集技术获取的指纹图像通常为二维灰度图像,其中脊线是暗的,而谷线是亮的。虽然指纹图像并不是深度图像,但是通过将灰度视为高度,可以将指纹显示为曲面(越黑越高),近似反映了实际手指皮肤上的高低起伏。成人脊线的宽度从0.1毫米到0.3毫米不等,脊线的周期约为0.5毫米。手指的轻微损伤,如表皮烧伤、擦伤或割伤,不会影响真皮层的脊线结构,新长出的皮肤还会恢复为原来的脊线结果。这就是指纹的终生不变性。

将指纹灰度图像表示为曲面(越黑越高),可近似反映实际手指皮肤上的高低起伏。
指纹的特征可以分为从粗到细的三个级别。第一级:脊线方向场和频率图(奇异点是方向场的特殊点);第二级:脊线骨架图(细节点是脊线的特殊点);第三级:脊线的内外轮廓(汗孔即内轮廓)。这些特征都是围绕脊线定义的,是有解剖学意义的。

指纹的三级特征(Feng和Jain,2011)
第一级特征并不描述具体的脊线,而是反映脊线的总体方向(脊线方向场)、疏密程度(脊线周期图或者频率图)。按照傅里叶分析的观点,如果把局部脊线图像看作二维正弦波,一级特征就是正弦波的方向和频率,而不包括相位。一级特征中的方向场尤其重要。方向场在指纹的多数区域是平滑的,但在个别区域呈现出独特的形状(表现为脊线曲率变大、大量脊线终止)。这些区域称为奇异点或者奇异区,有两种基本类型:环形和三角形(见下图)。当两个环形奇异点距离很近时,会形成螺旋形的奇异点。螺旋形奇异点是复合奇异点,而不是基本的奇异点。按照数学公式,仅用奇异点的位置和类型,就可以近似拟合出原始方向场;因此奇异点可以看作是方向场的非常紧致(compact)的表示。

环形和三角形是基本的奇异点类型,一对环形奇异点构成螺旋形奇异点。核心点(core)可视为指纹的中心,作为指纹坐标系的原点。
根据奇异点的分布和数量可以将指纹分为不同纹型(见下图),可用于人工和自动指纹检索。奇异点通常位于手指中央,由于这个区域能够确定指纹纹型,这个区域也称为模式区(pattern area)。奇异点还可以用来定义指纹的坐标系,将不同指纹对齐,方便指纹匹配、指纹大库检索、以及指纹模板保护。

五种类型的指纹:左箕型、右箕型、斗型、弓型、尖弓型
第二级特征记录具体脊线的位置,重点是它结束和分叉的地方,但是并不关注脊线的内外轮廓等细节(脊线不是数学中的线)。脊线突然结束和分叉的地方,称为细节点(minutia)。细节点是人工和自动指纹比对最常用的特征。Galton(1892)最早定义了指纹细节点并观察到它们终生不变。在比较完整的指纹中(如滚动滚动),细节点的数量可以超过100个。实际中,仅需少量(例如,12-15个)匹配细节点就足以推断两个指纹来自同一根手指。按照Champod等人(2016)的估计,奇异区内和奇异区外的细节点平均密度分别为每平方毫米0.49和0.18个。虽然专家在人工比对中可能利用多种类型的细节点(几种常见类型如下图所示),但是指纹识别算法通常只考虑两种基本类型,因为其他复合细节点类型可以表示为结束点和分叉点的组合,而且自动识别不同细节点类型会引入错误。主要的指纹数据标准(ISO/IEC 19794-2,2011;ANSI/NIST-ITL 1-2011,2015)也仅考虑结束点和分叉点。由于细节点的属性至少包括位置和角度,实际上指纹的细节点集合包含了大量的一级特征。按照Feng和Jain(2011)的重建算法,仅用细节点的位置和角度,就可以近似重建出脊线图。因此细节点可以看作是脊线图的非常紧致的表示。

前两类(结束点和分叉点)是最基本的细节点类型,其余可以看作一对邻近细节点的各种组合。
第三级特征是关于脊线的各种细节属性。脊线并不是线,它有宽度、形状、外轮廓、汗孔,还会被褶皱打断。此外还有被指纹脊线提取算法通常忽略的不成熟脊线(incipient ridge)。手指表皮的每条脊线都分布着汗孔,并向下连通到真皮上(Roddy和Stosz,1997)。汗孔尺寸大约为60~250微米。据观察,沿一厘米脊线上汗孔的数量大约9到18个。据称,在指纹足够清晰的情况下,20到40个连续分布的汗孔足以确定一个人的身份(Ashbaugh,1999)。尽管三级特征对于现场指纹鉴定专家非常重要,但目前很少有自动匹配技术使用它们,因为即便使用高分辨率指纹采集器(例如1000 dpi)也无法保证能采集和稳定提取到汗孔(Zhang等,2011a;Zhao和Jain,2010)。尽管实际算法使用较少,由于CDEFFS委员会(2008)的工作,ANSI/NIST-ITL 1-2011(2015)的第9类记录还是包含了第三级特征。

指纹的三级特征包括(a)汗孔、脊线外轮廓,(b)不成熟脊线,(c)褶皱。
上述特征都是具有解剖学意义的指纹特征(例如,脊线、奇异点、细节点、汗孔)。从指纹图像还可以提取没有明确解剖学意义的特征,SIFT关键点、深度网络特征。这些特征也能用于指纹匹配,详细介绍见指纹匹配综述。本文主要讨论具有明确解剖学意义的三级特征的提取。下图显示了提取细节点的典型处理步骤。指纹特征提取通常按照一、二、三级的顺序进行,因为下一级特征的提取需要上一级特征的指导,才能抵御噪声干扰。下面的章节就按照这样的顺序组织。
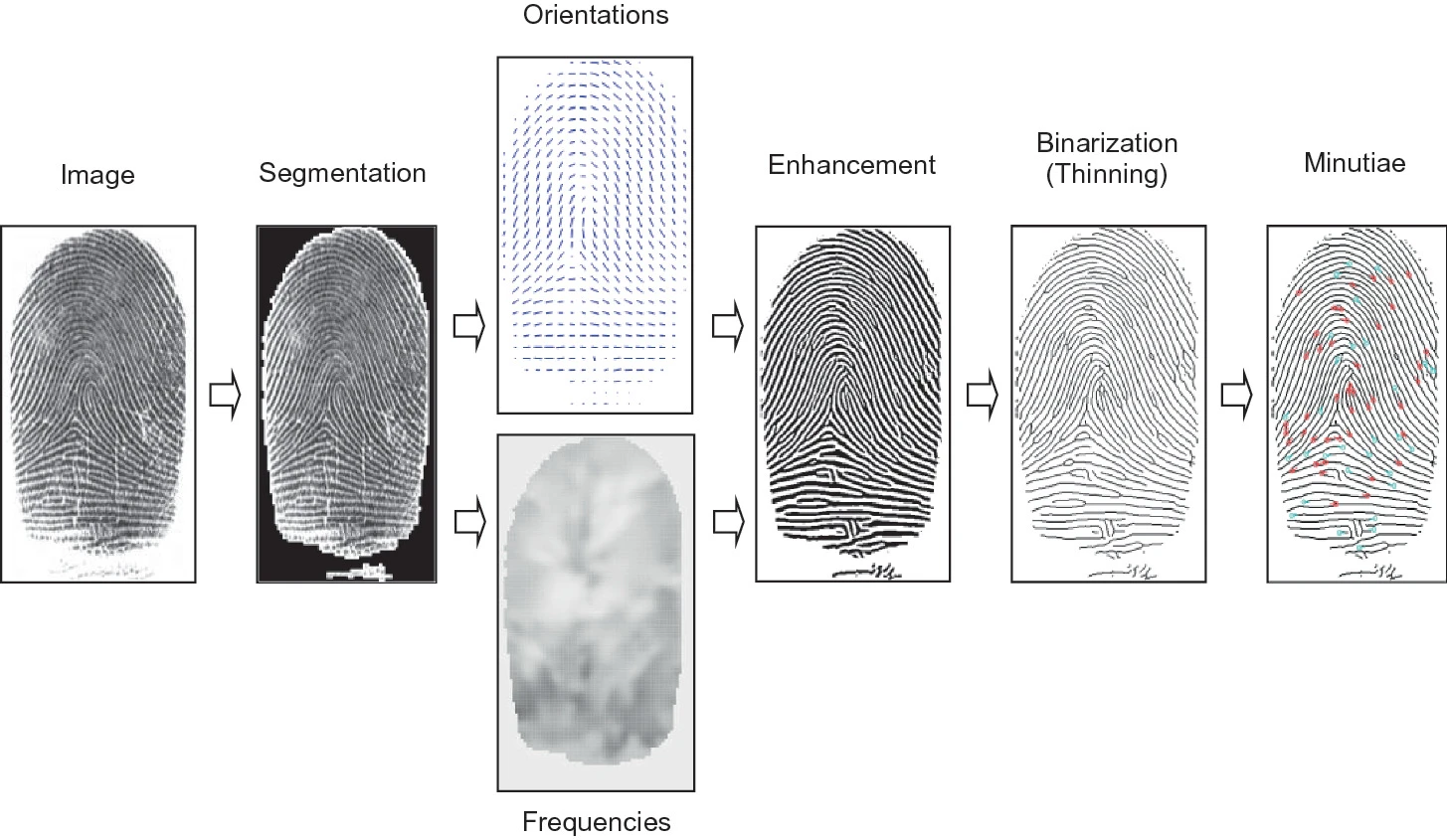
从指纹提取细节点的典型流程
2、指纹区域分割
指纹区域分割是指将指纹图像中的指纹区域(前景)与背景分开。分割的示例如下图所示。分割有助于提高后续运算的速度,并避免背景中的虚假特征。
这里分割特指从包含单指的图像中分割出指纹。对于包含多个指纹的图像,例如四连指图像(slap),有专门设计的指纹分割算法分割出各个指纹,并识别每个指纹的具体指位(例如,右手中指)。这里的分割方法均针对接触式指纹图像,而不讨论非接触指纹的分割。对于背景简单的非接触指纹图像(例如使用专用的非接触指纹采集器),这里的分割方法应该可以处理。但是对于复杂的情况(例如在非常复杂的背景下,用手机拍摄的指纹图像),可能需要用到更专门或者更复杂的分割方法(如基于深度学习)。
由于指纹图像是条纹图案(暗带和亮带),因此使用全局或局部阈值技术(Gonzales & Woods,2007)不允许将指纹区域与背景有效隔离。事实上,真正区分前景和背景的不是平均图像强度,而是前景中是否存在条纹和定向图案,以及背景中是否存在各向同性图案(即没有主导方向)。如果图像背景始终均匀且比指纹区域亮,则基于局部强度阈值的简单方法可以有效地区分前景和背景。在实践中,存在噪声(例如手指表面或实时扫描指纹扫描仪表面的灰尘和油脂产生的噪声)需要更强大的分割技术。
2.1 经验特征+阈值
为了区分指纹前景和背景,研究者提出了多种从局部图像块提取的特征:
- 局部脊线方向直方图中存在显著峰值(Mehtre等,1987)。
- 垂直脊线方向上的灰度方差(Ratha等,1995)(见下图的示例)。
- 每个图像块中梯度的平均幅度(Maio和Maltoni,1997)。
- Gabor滤波响应的方差(Shen等,2001;Alonso-Fernandez等,2005;Wang等,2005)。
- 傅里叶谱的局部能量(Pais Barreto Marques和Thome,2005;Chikkerur等,2007)。

Ratha等人(1995)的指纹前景分割示例
提取这些特征后,使用全局阈值就可以得到分割结果。上述方法的速度非常快,当背景较为简单时,表现也不错。但是对于比较复杂的背景,需要使用下面要介绍的更强大的方法。
2.2 简单分类器
引入了基于学习的技术,以获得基于特征值阈值的方法的更准确的分割:
- Bazen和Gerez(2001)提出了一种逐像素分割方法。作者在每个像素的邻域中计算三个特征(梯度一致性、灰度平均值和灰度方差),然后利用线性分类器将每个像素分为背景或前景。线性分类器的最佳参数可以针对特定指纹传感器进行优化。最后还执行形态学后处理(Gonzales和Woods,2007)以消除前景和背景中的空洞,并使指纹区域的外部轮廓更规整。Yin 等人(2005)使用相同的特征向量进行逐点分割,将超平面(线性分类器)改为二次分割面(非线性分类器),提高了分割性能。
- Chen等人(2004a)提取块聚类程度、局部灰度平均值和全局灰度平均值的差异、以及块方差三种特征,利用线性分类器进行像素级分割,最后做形态学后处理。这里的块聚类程度是一种衡量脊和谷灰度聚类的度量。下图显示了三个例子。
- Paiva和Tasdizen(2012)认为,指纹块在高维空间中可以形成了一个简单且高度规则的圆形流形。因此,他们引入了一些特征来表征流形拓扑,并训练了Fisher线性分类器(Duda等,2000)来区分前景和背景块。

Chen等人(2004a)的指纹分割示例
2.3 全变分
全变分(total variation, TV)模型已广泛用于图像分解(Aujol等,2006;Buades等,2010)。研究者将这些技术应用于分割最困难的指纹——现场指纹(Zhang等,2013;Cao等,2014)。
TV方法将输入图像分解为两层:卡通(cartoon)和纹理。现场指纹图像的卡通层通常包含结构化噪声(笔画、文字、污渍、斑点等),对应于背景,而纹理层包含代表指纹的纹理成分。经过卡通和纹理的分解后,可以使用传统的分割方法从纹理层中分割出指纹区域。
Zhang等人(2012a,2012b,2013)提出的方法通过根据背景噪声水平局部调整卡通和纹理的相对强度,并施加方向信息来扩展经典TV方法。Thai和Gottschlich(2016)提出了三层分解(卡通、纹理和噪声),他们的方法加强了纹理层的稀疏性和平滑度。如下图所示,TV方法对于一些复杂的现场指纹可以取得不错的分割结果。但是,这种方法并不能分离粘连的多个现场指纹,而且运算量很高。

Zhang等人(2013)的现场指纹分割示例
2.4 深度学习方法
一些研究者提出了基于深度学习的现场指纹分割方法:
- Zhu等人(2017)使用多尺度块训练了四个CNN,并融合了相应的输出分数以提高分割精度。
- Ezeobiejesi和Bhanu(2017)使用一组受限玻尔兹曼机(RBM)实现生成特征学习模型,并利用二分类器对每个指纹块的特征进行分类。
- 这两种方法都是单独处理图像块(即通过滑动窗口方法),使得计算效率偏低。Nguyen等人(2018a)结合了全卷积网络和基于检测的方法,一次性处理整个输入图像。作者还通过视觉注意机制仅关注现场指纹区域。
3、脊线方向场估计
估计局部脊线方向(其整体称为方向场)是指纹特征提取中最重要的步骤之一,它对于许多后续任务的影响很大,包括脊线频率估计、脊线增强、指纹匹配等。
像素
[
x
,
y
]
[x, y]
[x,y]处的局部脊线方向是脊线穿过以
[
x
,
y
]
[x, y]
[x,y]为中心的任意小邻域与水平轴形成的角度
θ
x
y
θ_{xy}
θxy,其范围是
[
0
,
180
°
]
[0,180°]
[0,180°]。由于方向场变化平缓,通常并不需要计算像素级的方向场,而只需要计算图像块级别的方向场,比如
8
×
8
8 \times 8
8×8大小的图像块。指纹方向场的概念最早见Grasselli(1969)。方向场的元素
θ
i
j
θ_{ij}
θij代表图像块
[
i
,
j
]
[i, j]
[i,j]中脊线的平均方向(见下图)。还可以附带定义方向可信度
r
i
j
r_{ij}
rij,以表示方向的可信度(或一致性)。在低质量区域,
r
i
j
r_{ij}
rij值较低;而在高质量脊线区域,
r
i
j
r_{ij}
rij较高。

指纹图像的脊线方向场
3.1 梯度法
梯度法是最基本的指纹方向场估计方法。图像
I
I
I在点
[
x
,
y
]
[x, y]
[x,y]处的梯度
∇
(
x
,
y
)
∇(x,y)
∇(x,y)是一个二维向量
[
∇
x
(
x
,
y
)
,
∇
y
(
x
,
y
)
]
[∇_x(x,y),∇_y(x,y)]
[∇x(x,y),∇y(x,y)],其中
∇
x
∇_x
∇x和
∇
y
∇_y
∇y分量分别是
x
x
x和
y
y
y方向的偏导。梯度方向代表图像灰度变化最大的方向,而梯度方向的法向代表穿过当前点的边缘方向
θ
θ
θ。
这种方法虽然简单高效,但也有一些缺点。首先,使用经典的Prewitt或Sobel卷积核来确定梯度的
∇
x
∇_x
∇x和
∇
y
∇_y
∇y分量,并根据
∇
y
/
∇
x
∇_y/∇_x
∇y/∇x的反正切计算
θ
θ
θ。由于90°左右的非线性和不连续性,这种做法是有问题的。其次,像素级的方向估计对指纹图像中的噪声非常敏感。此外,简单地算平均角度是没有意义的。例如,5°和175°之间的平均方向不是90°(算术平均值),而应该是0°。此外,平均方向并不好定义。考虑两个正交方向0°和90°,其平均方向是45°还是135°?
Kass和Witkin(1987)为上述问题提出了一个简单而优雅的解决方案,它允许对局部梯度估计进行平均。他们的基本思想是将角度加倍,以便每个方向估计都由矢量编码:
d
=
[
r
cos
(
2
θ
)
,
r
sin
(
2
θ
)
]
d=[r \cos(2\theta), r \sin(2\theta)]
d=[rcos(2θ),rsin(2θ)]其中,可靠性
r
r
r与方向估计强度成正比(例如梯度幅度)。通过分别对局部
n
×
n
n \times n
n×n 窗口中的两个分量求平均值,可以得到方向的平均值。
d
ˉ
=
[
1
n
2
∑
r
cos
(
2
θ
)
,
1
n
2
∑
r
sin
(
2
θ
)
]
\bar{d}=\left[ \frac{1}{n^2} \sum r \cos(2\theta), \frac{1}{n^2} \sum r \sin(2\theta) \right]
dˉ=[n21∑rcos(2θ),n21∑rsin(2θ)]如果用上式计算两个正交方向之间的平均值,结果向量的长度为零,表明平均方向是无意义的。

梯度法得到的方向场和一致性图
3.2 长条法和投影法
长条法就是定义了一组离散方向(长条),通过分析长条上的灰度信息,选择最优的长条作为当前位置的脊线方向。
Stock和Swonger(1969)对沿八个长条(slit)的像素灰度值求和,并分别为脊或谷像素选择最小和长条或最大和长条。事实上,对于位于脊上的像素(深色),沿脊线方向的灰度值之和很小,而对于位于谷上的像素,总和很高。
一种合理的假设是,沿着脊线方向灰度的总波动最小,而在正交方向上波动最大。Mehtre等人(1987)、He等人(2003)、以及 Oliveira和Leite (2008)的方法均是利用这样的假设。特别是,Oliveira和Leite(2008)计算了对应于每个长条的像素灰度的标准偏差,并根据长条与其正交长条之间的最大标准差对比度选择最佳长条(见下图)。

如果一个长条与脊线平行,它和垂直方向长条内的灰度方差差异会很大。
Sherlock(2004)建议沿多个离散方向投影局部窗口内的脊线;表现出最小变化的投影对应于脊线的方向。在Ji和Yi(2008)方法中,在计算投影之前,除中心线外的所有脊线都从局部窗口中移除。
基于长条和投影的方法的计算复杂性通常高于梯度法,并且量化可能会产生更粗糙的角度分辨率。但是,这些方法允许为每个离散方向分配一个概率值,该值可用于进一步处理噪声区域。换句话说,基于梯度的技术导致赢家通吃的决定,其中只输出了最佳方向;而在基于长条和投影的方法中,次优方向的概率可以给后面的处理提供信息。
3.3 频域法
Kamei和Mizoguchi(1995)的方法(Kamei(2004)有更详细的描述)利用了频域中的16个方向滤波器。作者在选择每个像素的最佳方向时,不仅根据最高滤波器响应,而且考虑局部平滑。Hong等人(1996)和Nakamura等人(2004)通过使用类似Gabor的滤波器,在空间域中实现了类似的效果。
Chikkerur等人(2007)基于短时傅里叶变换(STFT)分析同时估计局部脊线方向和频率。
3.4 方向场平滑
从低质量指纹计算得出的方向场可能包含许多错误。许多时候,局部平滑是非常有效的(见下图)。

局部平滑可以去除大部分噪声,但是也会导致奇异点偏移。
然而,简单的平滑有几个缺点:
- 当不正确的方向是压倒多数时,平滑无效。
- 在高曲率地方(尤其是在奇异区域),平滑无效,甚至会导致奇异点偏移(见上图靠下方的环形奇异点)。
为了克服上述不良影响,研究者提出了各种比简单平滑更细致的方法:
- Jiang等人(2004)指出,当有噪声的方向场被平滑时,局部一致性趋于增加。而如果平滑了高曲率区域,则方向场局部一致性仍然较低。为了防止平滑高曲率区域,可以根据层次一致性分析选择平滑窗口的大小。Can和Lin(2009)也是类似的方法。
- Liu等人(2004)认为,由于许多噪声是由脊线上的疤痕和断裂引起的,因此可以将其建模为脉冲函数。为了抑制这种噪声,简单的平滑(即线性滤波)是无效的,而类似于中值滤波的非线性方法表现更好。
- Zhu等人(2006)训练了一个神经网络,基于11维特征向量,将局部方向分为两类:正确和不正确。对于每个元素,从相应的图像块中提取11个特征,包括梯度幅度、灰度方差、沿方向投影的灰度方差、脊线间距离和峰/谷高度方差等。分类后,使用相邻的正确方向纠正不正确的方向。
- Zhang和Yan(2007)将前景中的无效区域定义为一致性差的连通集,并使用这些区域的轮廓来构建约束的Delaunay三角测量,用于通过插值校正方向。
- Oliveira和Leite(2008)提出基于多尺度分析的方向场修正。他们在两个不同的尺度(小尺度和大尺度)下计算方向场,并仅修正两个方向场之间差异很大的元素;如果差异不大,则保留小尺度的方向;否则,用大尺度的方向修正小尺度的方向。Mei等人(2009)提出了另一种多分辨率方法。
- 一些研究者提出用扩散模型来平滑方向场(Perona,1998)。Hou和Yau(2010)的变分方法试图在平滑方向场的同时,保持奇异点位置不变。Cao等人(2012)的模型考虑了方向向量场的散度和旋度的分布。通常,这些技术需要通过迭代数值方法求解非线性微分方程。
3.5 全局模型
指纹方向场的全局数学模型有多种用途,例如方向场校正、方向场压缩和方向场合成。根据是否明确建模奇异点,可以把这些模型分两类。
3.5.1 基于奇异点的模型
Sherlock和Monro(1993)提出的数学模型,仅从奇异点的位置合成指纹方向场。这种模型也称为零极点模型,因为它将环形奇异点作为复平面中的零点,三角形奇异点作为复平面中的极点。但是,该模型做出了过于简化的假设,并没有涵盖所有可能的指纹方向场模式(具有不同方向场的指纹可能具有相同的奇异点分布)。Vizcaya和Gerhardt(1996)和Araque等人(2002)对这种方法进行了改进。Vizcaya和Gerhardt(1996)通过使用围绕奇点的分段线性近似来调整零点和极点的行为,从而改进了零极模型。这些新模型引入了额外的自由度,以更好地建模指纹方向场的多样性。他们还提出了一种基于梯度下降的优化技术,从方向场计算模型参数。
在上述方法中,奇异点对给定坐标处脊线方向的影响与该点与奇异点的距离无关;这可能会导致远离奇异点的区域出现错误。此外,这些模型无法处理没有奇异点的指纹,例如平弓型指纹(plain arch)。Zhou和Gu(2004b)提出了一个有理复函数模型,该模型通过添加一些伪零点和伪极点作为控制点来推广零极点模型。伪零点是分子中附加多项式的根,伪极点是分母中附加多项式的根。模型参数可以用加权最小二乘优化(WLS)从奇异点位置和方向场得出。Zhou和Gu(2004a)和Gu等人(2006)的模型是同类方法。
Li等人(2006)认为,一个好的方向场模型不仅应该准确地近似方向场,而且还应该在脊线信息不可用的情况下(例如,由于强噪声)具有预测能力。Li等人(2006)提出的方法使用一阶相图(phase portrait)方法来计算预测的方向。这允许使用奇异点周围的数据重建方向场。为了提高预测精度,通过将不可靠的方向替换为预测的方向来优化方向场的初始估计(通过梯度法计算的)。然后基于修正后的方向场,使用约束非线性相图法获得最终方向场模型。
Huckemann等人(2008)认为,在Sherlock和Monro模型之后提出的大多数全局模型都由太多参数控制,因此从给定的方向场中提取稳定的参数值至关重要。他们的模型,称为二次微分(QD),扩展了Sherlock和Monro(1993)零极模型,通过使用五个具有明确几何意义的值作为控制参数(除了奇异点位置):三个参数控制手指相对于图像的位置(即参考轴的原点和角度),其余两个参数定义手指的水平和垂直尺寸。Gottschlich等人(2017)提出的XQD是对上述方法的扩展。
上述所有建模方法都依赖于奇异点的位置和底层的优化技术,但对于是首先基于有噪声的方向场计算奇异点,还是基于不准确的奇异点改进方向场,这些方法并没有提及。Dass(2004)提出的贝叶斯模型允许同时提取方向场和奇异点,克服了上述缺点。他通过考虑局部邻域中的空间平滑度、梯度值以及奇异点对局部方向的贡献,对方向场进行迭代更新。同时获取方向场和奇异点信息提供了交错更新的额外优势:可以根据当前的奇异点信息动态改进方向场,并且由于改进了方向场,可以更高精度地提取奇异点。然而,联合估计二者的数值优化方法非常耗时。
3.5.2 不依赖奇异点的模型
方向场还可以用不依赖奇异点的正交多项式建模。模型系数通过对初始的粗略估计进行数据拟合得到。
- Wang等人(2007a)提出了一种基于二维傅里叶级数展开(FOMFE)的指纹方向场模型。该模型可以无缝汇总全局特征,包括奇异点周围的高曲率区域。Wang和Hu(2011)的扩展版本可以从部分指纹重建全局方向场。
- Ram等人(2010)使用勒让德(Legendre)多项式独立建模方向场的正弦和余弦分量。Jirachaweng等人(2011)提出在基本模型不能很好地拟合数据的区域(例如,奇异点),使用高阶勒让德多项式进行细化。
- Liu和Liu(2012)提出把离散余弦变换(DCT)用作基函数。方向场由DCT基函数的线性组合重建,并使用稀疏编码来提高对噪声的鲁棒性。
3.6 机器学习法
前述的方向场估计方法对于指纹的先验知识利用不足,对于极低质量的指纹效果不佳。字典法(Feng等,2013)开启了基于机器学习的指纹方向场估计方法,把尽可能利用先验知识作为提高性能的主要手段。2015年之后,研究者逐渐开始将深度学习技术用于指纹方向场估计。本节只讨论基于传统机器学习的方法(主要是字典方法)。基于深度学习的方向场估计方法详见指纹识别综述(10): 深度学习方法。
3.6.1 全局字典法
受自然语言处理中使用的拼写校正技术的启发,Feng等人(2013)提出了一种有效的方法来利用指纹方向场的先验知识。在离线阶段,作者收集了一批从高质量指纹得到的真实方向场,通过聚类构建出方向块字典(下图)。

方向块字典(Feng等,2013)
在在线阶段,先用局部的估计技术(例如,STFT)实现初始方向场估计,然后将方向图划分为重叠的块,对于每个块,在字典查找到六个最相似的方向块单词。最后用经典的优化方法使一个能量函数最小化,就可以得到每个块的最佳方向块单词。该能量函数包含两项,第一项反映的是方向块单词和初始方向场的相似程度,另外一项反映的是相邻方向块单词之间的兼容性。下图显示了该方法的流程。

Feng等人(2013)的全局字典法
作者在NIST SD27现场指纹库上进行了实验,发现该方法的性能显著优于之前的方向场估计方法(FOMFE方法,STFT方法)。下图为一些示例。

Feng等人(2013)的全局字典法对于一些现场指纹的估计结果
3.6.2 局部字典法
Yang等人(2014)对于全局字典法进行了深入分析,发现它可能在不合理的地方出现局部合理的方向块,例如在手指上部出现三角形奇异点。

Yang等人(2014)发现全局字典法可能在不合理的地方出现局部合理的方向块。
作者提出对手指不同区域使用不同的局部方向块词典,以避免这种错误。然而,局部方向块词典的前提,是要把指纹调整到统一姿态。这对于现场指纹来说是很有难度的。为此,作者提出利用所有局部块进行概率投票(一种广义霍夫变换方法),估计指纹姿态(详见第6节姿态估计)。除此之外的步骤与全局字典法类似(流程图见下图)。

Yang等人(2014)的局部字典法
作者在两个现场指纹库上进行了实验,发现局部字典方法总体上优于全局字典方法。下面是全局和局部字典法在3个例子上的对比。

全局和局部字典法在3个例子上的对比(Yang等,2014)
3.7 评测
有两种评估方向场估计算法的方法:(1)直接评估:计算算法输出的方向场与方向场真值的误差;(2)间接评估:通过后续任务的性能反映方向场估计的性能(例如,奇异点检测、细节点提取、指纹匹配的性能)。由于间接评估与后续算法相关,不同论文的间接评估不好对比,这里只讨论直接评估。
FVC-onGoing评测系列中的指纹方向场估计评测(FOE)是专门设计用于评估方向提取算法准确性的基准。FOE使用的指纹图像是指纹采集器得到的平面指纹图像,分为高质量和低质量两个类别。一些针对现场指纹的方法也可以应用于该数据集,因为低质量图像与现场指纹类似。组织者在指纹选定位置手工标注方向,然后插值得到方向场真值。虽然手工标注不一定很精确(Schuch等,2017b),但是低质量类别的误差可以反映当前最高水平(见下表)。从该表可以看出,基于学习的技术(局部词典和CNN)对低质量图像的优势是很显然的。然而,它们的计算复杂性通常远高于梯度法。FVC-onGoing评测的一个不足是它是基于CPU的计算平台,而许多深度学习方法需要GPU支持。
FVC-onGoing指纹方向场估计评测中代表性方法的性能。主要看低质量类别(AvgError bad)。
MethodAvgError bad (°)AvgError good (°)Computation time on Intel Xeon E5410 (s)CNN DEX-OF (Schuch et al., 2017a)6.734.841.776Local dictionary (Yang et al., 2014)9.666.085.987ROF (Div-Curl model) (Cao et al., 2012)11.205.240.762Adaptive polynomials (Turroni et al., 2011)13.275.934.772FOMFE (Wang et al., 2007a)21.446.701.996Gradient (baseline) (Turroni et al., 2011)21.835.860.074
大多数现场指纹方向场估计算法是在NIST SD27指纹库进行的评测,作为真值的手动标注方向场来自(Feng等,2013)。下表比较了不同现场指纹方向场估计算法的性能。可以看出,最新的基于深度学习的方法取得了最佳性能。
NIST SD27数据库及其3个子集上各方向场估计算法的均方根偏差(RMSD)
方法全部GoodBadUglyGlobal Dictionary (Feng等,2013)18.4414.4019.1821.88Local Dictionary (Yang等,2014)14.3511.1515.1516.85RidgeDict (Cao等,2014)19.5315.3420.7022.68ConvNet (Cao和Jain,2015)13.5110.7613.9416.00ExhaustiveSearch (Yin等,2018)13.0110.8513.9914.27FPRefNet (Duan等,2021)12.169.8712.8313.85
4、脊线频率图估计
指纹的局部脊线频率(其倒数为局部脊线周期)是指沿局部脊线法向单位长度内的脊线数。局部脊线频率的主要用途是确定脊线增强的参数。此外,脊线频率图还被用于指纹扭曲矫正、指纹匹配和检索任务。
局部脊频周期在不同的手指上有所不同,在同一指纹的不同区域之间也可能存在明显变化(见下图)。Orczyk和Wieclaw(2011)基于指纹专家的手动标注进行了统计,在500 dpi指纹中,大多数局部脊线周期是5到10像素,平均为7.71像素。

两个指纹图像和相应的频率图像是用Maio和Maltoni(1998a)提出的方法计算的。在频率估计后执行局部 平滑以降低噪声。亮块表示更高的频率。很明显,不同的指纹区域可能有明显频率变化,并且不同的手指可能具有不同的平均频率。
Hong等人(1998)通过计算沿局部脊方向垂直方向的两个连续灰度水平峰值之间的平均像素数来估计局部脊频率(见下图)。该方法简单快捷。然而,在噪声指纹图像中,很难可靠地检测空间域中连续的灰度峰值。在这种情况下,作者建议使用插值和低通滤波。

Hong等人(1998)利用x签名方法计算局部脊线频率
Gottschlich(2012)认为,x签名方法的大多数频率估计误差发生在无法定义单个主导方向的高曲率区域(例如,接近奇异点)。因此,他建议在计算x签名之前,根据脊线曲率对脊线进行局部校正(见下图)。脊线拉直后,还可以增大计算频率的窗口尺寸,提高估计的鲁棒性。

Gottschlich(2012)将脊线拉直,改善x签名频率计算方法
Kovacs-Vajna等人(2000)的方法分两步:首先,将图像分为
64
×
64
64 \times 64
64×64大小的块,在质量较好的图像块计算平均脊线距离,然后根据扩散方程将此信息传播到其余区域。第一步有两种方法:几何方法和频谱分析方法。Chikkerur等人(2007)基于短时傅里叶变换(STFT)分析同时计算局部脊线方向和频率。Zhan等人(2006)比较了在空域和频域中运行的频率估计方法,并得出结论,前者的效率高,但后者似乎对噪声更可靠。
5、奇异点检测
奇异点是指纹最明显的一级特征,可用于指纹分类以及指纹对齐等任务。完整指纹中奇异点的数量很有规律,平弓没有奇异点,箕和尖弓有一对环形和三角形奇异点,斗型有两对环形和三角形奇异点。奇异点位置的空间分布也存在规律(Cappelli和Maltoni,2009)。大多数奇异点检测方法是通过分析方向场;早期的方法通常只做局部分析,但也有一些方法明确利用奇异点的总体规律。下面分别介绍基于庞加莱指数的方法、方向场复滤波法、以及全局建模方法。最后一节介绍与奇异点非常相关的姿态估计问题。
5.1 庞加莱指数法
设
G
\boldsymbol{G}
G为与指纹方向场关联的离散向量场(注意,指纹方向场不是真正的向量场,因为它的元素在
[
0...180
°
)
[0...180°)
[0...180°)),
C
C
C为
G
\boldsymbol{G}
G中的曲线。庞加莱指数
P
G
,
C
P_{\boldsymbol{G},C}
PG,C定义为沿
C
C
C上
G
\boldsymbol{G}
G的向量的总旋转角。要计算指纹
[
i
,
j
]
[i,j]
[i,j]处的庞加莱指数
P
G
,
C
(
i
,
j
)
P_{\boldsymbol{G},C}(i,j)
PG,C(i,j),可沿着将
[
i
,
j
]
[i,j]
[i,j]包含在内的封闭路径
C
C
C,计算向量的累计变化。对于不同的
C
C
C,计算结果可能不同。
可以证明,在闭合曲线上,庞加莱指数只能是以下值:0°(非奇异点)、180°(环形奇异点)、 -180°(三角形奇异点)和360°(螺旋形奇异点)。下图显示的是在8近邻构成的封闭路径上计算庞加莱指数。

三种情况的庞加莱指数
Bazen和Gerez(2002)提出了用于定位奇异点的庞加莱方法的一个有趣实现。根据格林定理,向量场上的闭环积分可以计算为该向量场旋转上的表面积分;实际中,作者不是对沿封闭路径对角度差异求和,而是计算方向图像的旋转,然后在每个元素的小邻域中执行局部积分。Bazen和Gerez(2002)还提出了一种为奇异点计算方向的方法。这是通过将每个检测到的奇异点周围的方向场与相同类型的理想奇异点的方向场进行比较得到的。
在低质量指纹上,庞加莱方法可能检测出虚假奇异点(下图)。通过平滑方向场通常有效地防止检测错误奇异点,不过它可能导致环形奇异点的位置发生偏移。Wang等人(2007b)提出了环形奇异点的校正,以补偿方向场平滑引入的偏移。

庞加莱指数方法对于方向场的噪声很敏感,容易得到一些错误奇异点;方向场平滑对此很有效。
一些研究者明确利用了奇异点的总体规律。考虑到完整指纹中只能存在有限数量的奇异点,Karu和Jain(1996)提出了迭代平滑方向场,直到庞加莱指数检测到有效数量的奇异点。
5.2 方向场复滤波法
Nilsson和Bigun(2002a,b,2003)的多分辨率分析方法是基于方向场的卷积。作者使用了两个复滤波器以检测旋转对称点。两个滤波器(一个用于环形奇异点,一个用于三角形奇异点)与方向场做卷积,任何一个滤波器响应较高的点被保留并以更精细的分辨率进行分析(见下图)。检测到的奇异点的方向也可以通过复滤波器响应的参数来估计。由于所用滤波器的可分离性,该技术可以高效运行。Chikkerur和Ratha(2005)对这种方法进行了改进。

Nilsson和Bigun(2003)奇异点检测方法的示例
5.3 全局建模法
利用方向场的全局模型可以提高奇异点检测的鲁棒性。Wu和Zhou(2004)使用零极模型和Hough变换检测奇异点。在零极模型中,每个奇异点周围的方向受其他奇异点的影响不大,因此,在局部窗口中,奇异点的位置和周围的方向受简单的线性方程约束。这使得实施投票方案成为可能。作者先用庞加莱方法得到奇异点的初始位置,然后检查每个点,通过霍夫变换细化其位置。Zhou等人(2009a)将庞加莱指数与另一个类似的运算符(称为DORIC)联合检测出一些初始的奇异点。作者将零极点模型方向场和估计方向场之间的差异作为目标函数,搜索使得目标函数最小的合理奇异点组合,作为最终结果。
Fan等人(2008)的方法也是基于零极模型和霍夫变换。为了细化奇异点的位置并排除虚假奇异点,作者还综合使用了庞加莱指数和伪脊线追踪方法(见下图)。

Fan等人(2008)奇异点检测方法的中间结果
Wang等人(2007a)利用他们的全局模型(FOMFE)获得了局部方向拓扑的解析表达式。每个点作为(普通点,环形或者三角形奇异点}的分类是由2×2矩阵(称为特征矩阵)的行列式符号确定。附加信息(如局部旋度和散度)可以用于消除错误奇异点(Wang和Hu,2008)。
6、姿态估计
指纹姿态估计是要确定指纹的参考中心和方向,定义一个稳定的物体坐标系。虽然姿态是比方向场、奇异点更高一层的特征(可以认为是0级特征),但是要把姿态估计的介绍放在方向场估计和奇异点检测之后。有两个原因:(1)姿态通常是基于奇异点和方向场定义的,(2)许多姿态估计方法是从一级特征来推测姿态。
指纹姿态可以对指纹特征提取和各种指纹匹配方法发挥基础性的作用。但是,长期以来指纹识别领域忽视(或者说回避)了指纹姿态估计问题。原因是大家普通认为指纹的姿态很难测量准确,而测得不准确就没法用,用了不准确的姿态对于本来很高的识别率有害。但是,近年来姿态估计的性能稳步提升,在方向场估计、指纹检索、指纹匹配上已经发挥了显著的作用。很有必要重新认识姿态在整个指纹识别体系中的基础性作用。
下面首先介绍早期的姿态估计方法。这些都是基于经验设计的算法,算法本身不直接利用训练样本。其中有的方法在质量不错的滚动指纹上可以得到较好的性能,但是对于质量差的滚动指纹、平面指纹、现场指纹,其估计性能就很不可靠了。
然后介绍基于传统机器学习的姿态估计方法。这些方法将姿态估计视为计算机视觉中的物体检测问题,早期的方法是基于概率投票(Yang等,2014)或者传统分类器(Su等,2016)。近年来,研究者提出了多种基于深度网络的姿态估计方法。基于深度学习的姿态估计方法详见指纹识别综述(10): 深度学习方法。

手指照片和指纹图像上显示的手指姿态(Yang等,2014)
6.1 经验方法
6.1.1 经验的参考中心检测方法
指纹核心点(core point)是常用的参考中心。如果指纹所有的奇异点都可以提取出来,核心点可以简单地定义为上方环形奇异点位置。但是平弓形指纹没有奇异点,因此还需要更普适的核心点定义。
Novikov和Kot(1998)将核心点定义为脊线法线的交叉点(见下图),并使用霍夫变换来确定其坐标。Rerkrai和Areekul(2000)采用类似的定义。由于脊线不能在核心点周围形成完美的同心圆,因此法线(下图的虚线)不会在单个点上完全交叉,须将平均点定义为核心点。Novikov和Kot(1998)用最小二乘法计算平均点,而 Rerkrai和Areekul(2000)计算法线对之间交叉点的重心。Areekul等人(2006)、Deerada等人(2020)是此类方法的改进。

脊线法线汇聚的位置可视为核心点
Jain等人(2000)提出了一种多分辨率方法,用于定位最上方的环形奇异点(核心点),该方法基于两个相邻区域
R
I
R_I
RI和
R
I
I
R_II
RII中正弦分量的积分(下图)。这两个区域的几何形状旨在捕获凹形脊线中的最大曲率。在每个尺度和每个候选位置上,方向场的正弦分量在两个区域上积分,从而产生值
S
R
I
SR_I
SRI和
S
R
I
I
SR_II
SRII。最大化
S
R
I
−
S
R
I
I
SR_I-SR_II
SRI−SRII的点被保留为候选位置,并以更精细的分辨率进行分析。

Jain等人(2000)计算核心点时采用的积分区域
Jiang等人(2004)设计了另一种多分辨率方法。他们选择在大尺度和精细尺度上都具有局部最小一致性的点作为核心点。这种方法能够在大约95%的FVC2000 DB2指纹图像中正确定位核心点。Van和Le(2009a)提出了上述技术的改进,其中方向一致性与曲率方向相结合。
受到Nilsson和Bigun(2003)以及Chikkerur和Ratha(2005)的复滤波方法的启发,Le和Van(2012)设计了一种新的复杂滤波器来检测基于方向对称性的核心点。与Nilsson和Bigun(2003)的抛物线对称滤波器相比,新滤波器还可以处理弓形指纹,并且能够更好地处理双箕斗。第二个运算符基于垂直方向变化,用于过滤掉不需要的奇异点(例如,双箕斗中最南端的环形奇异点)或错误检测。作者报告说,FVC2004 DB1的检测准确率为 96.6%。
对于质量较好的滚动指纹、正面按压的完整的平面指纹,上述方法的性能还不错;但是对于核心点缺失的残缺指纹、核心点区域质量很差的指纹,这些方法不够鲁棒。
6.1.2 经验的参考方向计算方法
参考方向有多种定义:(1)外部指纹轮廓的形状(如果有的话),(2)核心三角区的方向(如果存在),(3)核心点邻域的平均脊线方向(下图),或(4)奇异点的方向(Bazen和Gerez,2002)。Li等人(2014)提出了一种特定的几何技术,使用一组等腰三角形测量弓形指纹的指纹方向。Hotz(2009)表明,垂直对称轴在弓形指纹中很容易地确定,而奇异点引起的干扰会对非弓形指纹中的计算产生负面影响。因此,他提出了一种基于模型的奇异点消除,以从所有类别的指纹中获得弓形图案。

Wegstein(1982)将核心点邻域的平均脊线方向作为指纹方向
6.2 机器学习的方法
6.2.1 参考方向场
利用参考方向场进行指纹对齐的大致想法最早见于Dai等人(2012)的掌纹姿态估计方法。不过,全掌纹的面积很大,包含了大量稳定的方向场信息,只需要少量参考方向场(已经手工对齐),就可以将输入掌纹对齐了。但是这种方法用在指纹上面临几个难题,包括不同纹型的方向场差异大,许多残缺指纹的面积很小,低质量指纹的方向场不准确,皮肤扭曲指纹的方向场也有扭曲。

利用参考方向场对齐掌纹(Dai等,2012)
Si等人(2015)的扭曲指纹矫正技术需要将输入指纹对齐到统一的姿态,然后才能做扭曲检测和矫正。为此,作者提出了一种基于大量参考指纹的姿态估计方法。作者用500个指纹作为参考指纹,包含清华扭曲指纹库中的前200组数据(200个正常指纹和对应的200个扭曲指纹)以及FVC2002 DB1A中的100个正常指纹。选用多个指纹做参考指纹是为了在在线阶段更好地对齐各种纹型的指纹,在参考指纹库中加入扭曲指纹是为了在在线阶段更好地对齐扭曲指纹。
在离线阶段,作者通过半自动方法得到所有参考指纹的中心和方向。如果利用基于庞加莱指数的方法能够准确检测到指纹的中心点,视偏上的中心点为指纹的中心。对于弓型指纹和那些偏上的中心点没有被准确检测到的指纹,作者采用人工辅助的方法标注指纹的中心。作者将垂直于指关节向上的方向定义为指纹的方向,人工标注了所有参考指纹的方向。由于参考指纹是在离线阶段进行配准的,所以能够接受人工标注的时间消耗。
在在线阶段,作者利用已配准好的多参考指纹(500个)对输入指纹进行配准。首先提取输入指纹的方向场,并用基于庞加莱指数的方法提取指纹的奇异点。根据输入指纹偏上的中心点是否被检测到,将配准分为两种情况。如果未检测到输入指纹偏上的中心点,通过全搜索(搜索空间包括参考指纹、姿态)来确定输入指纹的姿态信息,以最小化参考方向场和输入方向场的差异。如果能检测到输入指纹偏上的中心点,将偏上的中心点移到固定坐标系的原点,搜索时不需要考虑平移参数,效率更高。
Si等人(2015)的姿态估计是为了后续的扭曲检测和矫正服务,没有对姿态估计性能进行单独的评测。
6.2.2 滑动窗检测
Su等人(2016)对于指纹中心的定义不同于之前的通常定义。从下图的四种类型指纹的例子,可以直观看出。

Su等人(2016)的指纹姿态定义
Su等人(2016)将指纹姿态估计视为一个物体检测问题来解决。基本流程是,在输入图像中滑动一个窗口,对于每个窗口提取方向场直方图特征;利用离线阶段训练好的分类器判断当前窗口图像是否为标准姿态的指纹;将分类器输出的判别分数视为窗口内包含标准姿态指纹图像的概率;选取分数最高的位置对应的中心位置作为指纹中心。
对于非直立的指纹,还需要估计指纹的倾斜角度。一种解决方法是将图像以不同角度分别进行旋转,在每个角度下重复上述中心位置的估计过程,然后选取判别分数最高的角度和中心位置作为最终估计结果。但是相对于判别时的内积计算,旋转图像的算法复杂度较高,为了加快估计过程,作者离线训练各个角度下的指纹分类器。在线估计时,使用各个角度下的分类器分别进行滑动检测,同样使用判别分数最高的分类器所对应的角度以及估计的中心位置作为最终估计结果。下图为在线估计指纹倾斜角度以及中心位置的流程示意图。

Su等人(2016)的指纹姿态估计方法
作者为了训练分类器收集的正样本是标准姿态的指纹,负样本是非标准姿态的指纹(见下图)。

正样本和负样本及其特征(Su等,2016)
作者从两个方面对姿态估计算法进行了评测,包括类内姿态一致性、姿态对于指纹检索性能的影响。类内姿态一致性是指对于相同指纹不同图像的姿态估计需要一致,这样才能用于指纹匹配和检索。作者用匹配细节点的位置和角度偏差来定量评价姿态估计算法对于相同指纹不同图像的一致性(见下图)。匹配细节点是由一个性能较好的细节点匹配算法自动得到。

Su等人(2016)用匹配细节点的位置和角度偏差来评价姿态估计算法对于相同指纹不同图像的一致性。(a)一对匹配指纹的姿态及其匹配细节点对。(b)使用姿态对齐两个指纹的细节点(相连的是匹配点)。在这个例子中,对齐后匹配细节点对的平均位置误差为46像素,平均角度误差是6.2度。
作者在NIST SD14数据库进行了批量测试,得出匹配细节点对方位误差的经验累积分布。从下图可看到,相比对比工作,该算法可以明显降低匹配细节点对的方位误差。98%的细节点对的位置偏差均在80像素以内,而在对齐之前则是接近300像素(图像大小为768x800像素)。接近99%的细节点的角度偏差在20度以内,在对齐之前则是接近30度。

不同姿态估计算法在NIST SD14数据库后2700对指纹上细节点方位误差的经验累积分布(Su等,2016)
下图的三对具体例子表明该算法的姿态一致性很好。

Su等人(2016)方法(蓝色)和前人方法在三对匹配指纹上的姿态估计结果。
作者利用估计的姿态改进了一个基于细节点的指纹检索算法。也就是说,要求匹配细节点的方位误差小于阈值。实验验证了使用姿态约束,可以显著降低指纹检索错误率。

Su等人(2016)利用姿态约束降低了基于细节点的指纹检索算法的错误率。
6.2.3 概率投票
Yang等人(2014)在研究现场指纹方向场估计问题时,分析了全局字典法(Feng等,2013)的缺陷,提出了局部字典法。但是,从现场指纹估计姿态,要比滚动指纹和平面指纹困难得多。现场指纹噪声强、变形严重、且面积很小,即便对于经验丰富的指纹鉴定专家,准确地标注姿态也是很难的。在这个问题上,之前没有公开的研究成果。

现场指纹的指纹中心经常缺失、被破坏或扭曲。
为了解决现场指纹的姿态估计问题,Yang等人(2014)研究了指纹不同区域的脊线方向分布,并建立了基于局部特征的统计模型。整个系统由两个阶段组成:在离线阶段,他们学习真实指纹方向块在指纹不同区域的空间分布,然后建立原型方向块的统计模型。在在线阶段,输入指纹的每个块都对指纹中心进行预测。然后将这些预测相加,并选择峰值作为输入指纹的最终姿态。
在离线阶段(流程见下图),作者首先从NIST SD4滚动指纹数据库中选择了398个高质量指纹作为训练集,然后手动标注它们的姿态和方向场。对于每个按照其姿态校正的训练方向场,一个4×4 窗口从上到下和从左到右滑动穿过图像。如果滑动窗口中的所有方向元素都有效,则方向块及其中心的坐标将添加到实际方向块训练集中。采用K中心聚类方法将所有方向块聚类为200个类,200个类中心形成原型方向块。最后,计算每个原型方向块的空间分布。

在离线阶段,从一组对齐的训练方向场学习原型方向块及其空间分布 (Yang等,2014)
在在线阶段(流程如下图),对于输入指纹,首先通过短时傅里叶变换(STFT)计算初始方向场。然后,一个4×4滑动窗口从上到下和从左到右滑过方向区域。在每个位置,找到最相似的原型方向块,并通过该原型的空间分布获得指纹中心的投票。通过将输入指纹所有位置的投票相加,可以计算出Hough图像,并选择峰值作为指纹中心的估计。

估计竖直的现场指纹中心的流程图 (Yang等,2014)
最后,将输入方向场以各种不同的角度旋转,并针对每个角度重复上述步骤以估计中心和相应的置信度值(流程见下图)。各角度最高值对应的中心和角度即最终的姿态。

未知方向的现场指纹的姿态估计。 (Yang等,2014)
该姿态估计算法的一些实验结果如下图所示。可以看出,尽管一些现场指纹缺少中心区域,该投票算法仍然可以很好地处理这种情况。不过,现场指纹的姿态估计仍然是一个很有挑战的问题,该方法对于许多现场指纹的姿态和真实姿态并不一致。所幸该姿态估计方法对于方向场估计问题够用了。如果要将其用于现场指纹匹配或检索,仍然需要进行大量改进。

NIST SD27中一些现场指纹的姿态估计结果(Yang等,2014)
Gu等人(2018)采用的中心定义与Si等人(2015)相同,是上方环形奇异点。原因是这项研究是针对平面指纹;而在平面指纹中,上方环形奇异点的出现概率远高于其余奇异点。作者首先利用Hough森林方法估计中心,然后将中心周围的方向场作为向量,利用SVM回归手指方向。算法的效率要高于(Yang等,2014;Si等,2015)。

Gu等人(2018)的指纹姿态估计流程
7、脊线增强
后续细节点提取算法和其他指纹识别技术的性能在很大程度上依赖于输入指纹图像的质量。在理想的指纹图像中,脊和谷交替并以局部恒定的方向流动。在这种情况下,可以轻松分割出脊线,并且可以精确定位细节点。然而,由于皮肤状况(例如,湿或干、割伤、脱皮)、传感器噪声、手指压力等因素,很大一部分指纹图像(比如大约10%)的质量很差。

好中差质量的指纹图像
这些不理想因素对于脊线的影响可以概括为:
- 脊线上存在许多中断;
- 相邻的脊线有粘连;
- 较大面积的脊线结构缺损。
这些使得在低质量区域提取脊线极其困难,进而会导致细节点提取出现以下问题:(1)提取了大量虚假细节点,(2)遗漏了大量真实细节点,以及(3)细节点的位置和方向存在较大误差。为了保证脊线和细节点提取算法在低质量指纹上取得良好性能,需要脊线增强算法来提高脊线结构的清晰度。
指纹鉴定专家通常能够通过使用各种视觉线索(例如局部脊线方向、脊线连续性等)来正确识别细节点。理论上,可以开发一种增强算法,利用这些视觉线索来提高脊线结构的质量。
根据提取脊线的难易度,可将指纹区域分为三类:
- 脊线清晰的区域:脊线连续且不和相邻脊线粘连;甚至脊线的三级特征也清晰可辨。
- 脊线可恢复的区域:脊线被少量折痕、污迹、粘连等破坏,但仍然大约可见,邻近区域提供了有关真实脊线结构的充分信息。
- 脊线不可恢复的区域:脊线被严重破坏,即使利用邻近区域的信息也无法可靠重建。

指纹图像中三种质量区域:脊线清晰、脊线可恢复、脊线不可恢复
脊线增强算法的目标是提高可恢复区域中脊线结构的清晰度,并将不可恢复区域标记为噪声太大而无法进一步处理。可以根据几个标准确定脊线清晰区域、可恢复区域和不可恢复区域;通常,图像对比度、方向一致性、脊线频率和其它局部特征可以组合在一起来定义指纹质量指标。由于指纹质量的估计对于许多算法和实际应用很重要,因此本文的最后会专门讨论质量计算。
7.1 点运算
点运算是指,每个像素的输出值仅取决于该像素的输入值和一些全局参数(而不取决于相邻像素的值)。常见的点运算包括对比度拉伸、直方图操作、均值方差归一化(Hong等人,1998)。点运算常作为更复杂的指纹增强算法的初始处理步骤。虽然点运算不能得到很强的指纹图像增强效果,但这一点在有时候是需要的。例如,指纹鉴定专家可能希望改善图像的对比度以方便观看,但是不希望产生虚假特征。
7.2 上下文滤波
最广泛使用的指纹图像增强技术是基于上下文过滤器。在传统的图像滤波中,只有一个滤波器用于整个图像的卷积。在上下文过滤中,滤波器特征会根据本地上下文而变化。通常,预先计算一组滤波器,并为每个图像区域选择其中一个滤波器。在指纹增强中,上下文通常由局部脊方向和局部脊频率定义。事实上,脊谷的正弦波主要由局部方向和频率定义,该方向和频率在整个指纹区域缓慢变化。根据局部脊频率和方向调谐的适当滤波器可以有效地消除不需要的噪声,并保持真正的脊和谷结构。
文献中已经提出了几种类型的上下文滤波器用于指纹增强。尽管它们有不同的定义,但预期行为几乎相同:(1)沿脊方向提供低通(平均)效果,目的是连接小间隙并填充由于孔隙或噪声引起的杂质,以及(2)在与脊正交的方向上执行带通(区分)效果,以增加脊和谷之间的区分并分离平行连接的脊。
上下文指纹增强的输出可以是灰度、近二进制或二进制图像,具体取决于所选的滤波器参数。在选择合适的滤波器集并调整其参数时,应该记住,目标不是产生图像的良好视觉外观,而是促进连续特征提取步骤的鲁棒性。由于在低质量区域,对局部环境(方向和频率)的估计可能是错误的,因此过于激进的过滤可能会产生虚假结构(Jiang,2001)。例如,Cappelli等人(2000年)(参见第7章)使用Gabor滤波器的迭代应用来生成合成指纹模式;在这种情况下,滤波器会生成不存在的脊模式。
7.2.1 空域滤波
匹配滤波器(O’Gorman和Nickerson,1989)和二维Gabor滤波器(Hong等,1998)对于脊线的增强效果不错。由于二者比较类似,下面介绍Gabor滤波方法。
Hong等人(1998)提出了一种基于二维Gabor滤波器的脊线增强方法,至今仍然被广泛应用。Gabor滤波器具有频率选择性和方向选择性,并且在空域和频域中都具有最佳的联合分辨率(Daugman,1985)。如下图所示,Gabor滤波器由正弦平面波(公式的第二项)与二维高斯函数(公式的第一项)定义。偶对称二维Gabor滤波器具有以下形式。
g
(
x
,
y
:
θ
,
f
)
=
exp
{
−
1
2
[
x
θ
2
σ
x
2
+
y
θ
2
σ
y
2
]
}
⋅
cos
(
2
π
f
⋅
x
θ
)
,
g\left( {x,y{:}\theta ,f} \right) = \exp \left\{ { - \frac{1}{2}\left[ {\frac{x_\theta^2 }{{\sigma_x^2 }} + \frac{y_\theta^2 }{{\sigma_y^2 }}} \right]} \right\} \cdot \cos \left( {2\pi f \cdot x_\theta } \right),
g(x,y:θ,f)=exp{−21[σx2xθ2+σy2yθ2]}⋅cos(2πf⋅xθ),其中
θ
θ
θ 是滤波器的方向,
[
x
θ
,
y
θ
]
[x_\theta,y_\theta]
[xθ,yθ] 是笛卡尔轴顺时针旋转
(
π
/
2
−
θ
)
(\pi/2-θ)
(π/2−θ) 角后的
[
x
,
y
]
[x,y]
[x,y] 坐标。在上述表达式中,
f
f
f 是正弦平面波的频率,
σ
x
σ_x
σx 和
σ
y
σ_y
σy 分别是高斯包络沿
x
x
x 轴和
y
y
y 轴的标准偏差。

一个偶对称Gabor滤波器的曲面和图像表示
要将Gabor滤波器应用于图像,必须指定四个参数(
θ
θ
θ,
f
f
f,
σ
x
σ_x
σx 和
σ
y
σ_y
σy )。显然,滤波器的频率完全由局部脊线频率决定,方向由局部脊线方向决定。选择
σ
x
σ_x
σx 和
σ
y
σ_y
σy 的值需要权衡取舍。值越大,滤波器对指纹图像中的噪声越可靠,但它们也更有可能产生虚假的脊线。另一方面,值越小,滤波器引入错误脊线的可能性就越小,但消除噪声的效果较差。实际上,从Gabor滤波器的调制传递函数(MTF)可以证明,增加
σ
x
σ_x
σx 和
σ
y
σ_y
σy会降低滤波器的带宽。根据经验,Hong等人(1998)设定
σ
x
=
σ
y
=
4
σ_x=σ_y=4
σx=σy=4。
为了加速,不是动态为每个像素计算最适合的Gabor滤波器,而是事先创建和存储滤波器组
{
g
i
j
(
x
,
y
)
∣
i
=
1
,
.
.
.
,
n
o
,
j
=
1
,
.
.
.
,
n
f
}
\left\{ g_{ij}(x, y) | i = 1,..., n_o, j = 1,..., n_f \right\}
{gij(x,y)∣i=1,...,no,j=1,...,nf},其中
n
o
n_o
no 是离散方向
{
θ
i
∣
i
=
1
,
.
.
.
,
n
o
}
\left\{θ_i | i = 1, ..., n_o\right\}
{θi∣i=1,...,no} 的数量,
n
f
n_f
nf 表示离散频率
{
f
j
∣
j
=
1
,
.
.
.
,
n
f
}
\left\{f_j | j = 1, ..., n_f\right\}
{fj∣j=1,...,nf}的数量。然后,对图像的每个像素
[
x
,
y
]
[x, y]
[x,y] 选择最接近方向和频率的滤波器
g
i
j
(
x
,
y
)
g_{ij}(x,y)
gij(x,y) 进行卷积。下图显示了
n
o
=
8
n_o = 8
no=8 和
n
f
=
3
n_f = 3
nf=3 的Gabor滤波器组。

一组Gabor滤波器
下图显示了基于Gabor滤波在三幅指纹图像上的应用效果。

Hong等人(1998)的Gabor滤波结果
7.2.2 频域滤波
Sherlock等人(1992,1994)在频域进行了指纹的上下文滤波。众所周知,空间域中的卷积对应于频域中的乘积。滤波器在频域中由以下函数定义:
H
(
ρ
,
θ
)
=
H
radial
(
ρ
)
⋅
H
angle
(
θ
)
,
H\left( {\rho ,\theta } \right) = H_{\text{radial}} \left( \rho \right) \cdot H_{\text{angle}} \left( \theta \right),
H(ρ,θ)=Hradial(ρ)⋅Hangle(θ),其中,
H
radial
H_{\text{radial}}
Hradial仅取决于局部脊线周期
ρ
=
1
/
f
ρ = 1/f
ρ=1/f,
H
angle
H_{\text{angle}}
Hangle仅取决于局部脊线方向
θ
θ
θ。
H
radial
H_{\text{radial}}
Hradial和
H
angle
H_{\text{angle}}
Hangle都被定义为带通滤波器,参数为平均值和带宽。一共定义出一组
n
n
n 个离散滤波器。为了减少滤波器的数量,局部脊线频率仅使用单个固定值,因此上下文仅由脊线方向确定。
n
n
n 个滤波器的傅里叶变换
P
i
,
i
=
1...
n
P_i, i = 1...n
Pi,i=1...n 可以预先计算。对输入指纹图像
I
I
I的滤波如下(见下图)。

Sherlock等人(1994)的频域脊线增强技术
- 计算 I \mathbf{I} I 的 FFT(快速傅里叶变换) F \mathbf{F} F。
- 每个滤波器 P i \mathbf{P}_i Pi 逐点乘以 F \mathbf{F} F,从而得到 n n n个滤波图像的变换 P F i , i = 1... n \mathbf{PF}_i, i = 1...n PFi,i=1...n。
- 为每个 P F i \mathbf{PF}_i PFi 计算反向 FFT,从而产生 n n n 个滤波图像 P I i , i = 1... n \mathbf{PI}_i, i = 1...n PIi,i=1...n。
- 为每个像素选择最接近方向滤波器的结果,得到增强图像 I enh \mathbf{I}_\text{enh} Ienh。
Chikkerur等人(2007)提出了一种基于短时傅里叶变换(STFT)的上下文滤波,该变换需要将图像划分为小的重叠块,并在每个块上分别执行傅里叶分析。计算每个块的脊线方向、脊线频率、方向一致性。然后用类似Sherlock等人(1994)的滤波器对每个块进行滤波。区别是,这里的角带宽根据方向一致性进行调整,而不是根据到最近奇异点的距离。由于奇异点检测不如方向一致性估计鲁棒,Chikkerur等人(2007)的带宽调整似乎比Sherlock等人(1994)的方法更有效。
7.2.3 滤波器选择
在低质量指纹中,有效增强的需求尤为重要,因为只有可恢复区域携带指纹匹配所需的信息。另一方面,在低质量的指纹图像中以足够的可靠性计算局部方向和频率特征是非常具有挑战性的。为了克服这个问题,Kamei和Mizoguchi(1995),Hong等人(1996),Bernard等人(2002)和Nakamura等人(2004)建议在图像的每个点应用所有滤波器。然后,用选择器从所有滤波器响应中选择最佳响应。
- Kamei和Mizoguchi(1995)通过最小化能量函数来进行选择,该能量函数包括方向和频率的局部平滑项。
- Hong等人(1996)和Nakamura等人(2004)的选择是基于对从滤波图像中提取的局部脊线分析。
- Bernard等人(2002)根据最大响应进行选择。然而,与大多数基于Gabor的方法不同,来自Gabor滤波器的实部和虚部的相位信息也用于最终的图像增强。
以上选择器的角色类似于局部脊线方向和频率估计。性能很难比拟近来更强大的基于学习的方向场估计方法。
7.3 机器学习方法
Rama和Namboodiri(2011)提出一种基于学习的指纹增强方法。该技术利用以前从一组干净的指纹中学习的模式来恢复有噪声的指纹。作者将分层互连的马尔可夫随机场用于处理多种分辨率的信息。此外,性能更强大的基于深度学习的脊线增强方法详见指纹识别综述(10): 深度学习方法。
8、细节点检测
大多数指纹识别系统是基于细节点匹配。因此,可靠的细节点提取是一项极其重要的任务,这方面有大量研究成果。多数方法是从二值图像(脊线增强图的二值化结果)提取。通常先对二值图像进行细化操作,将脊线宽度减少到一个像素,产生骨架图像。然后,逐像素扫描检测细节点。
还一些研究者提出了直接在灰度图像上提取细节点,而无需经过二值化和细化步骤。做出这一选择是出于以下考虑:
- 二值化过程会丢失许多信息,并且细化可能会引入虚假细节点;
- 细化运算可能比较耗时。
上述方法得到的细节点难免有许多虚假点,尤其是在指纹边界会有大量的结束点。因此通常需要细节点过滤的步骤,以删除虚假点。
最近,研究者已经提出了基于深度学习的技术,由端到端训练的单个模型实现整个细节点提取流程,涵盖了局部脊线方向和频率估计、脊线增强、细节点检测和过滤。详见指纹识别综述(10): 深度学习方法。
8.1 从二值图像检测
对于经过脊线增强的指纹,简单的全局阈值或者局部阈值法就可以得到不错的二值图像。为了去除二值图中的噪声(空洞、孤立点、毛刺等),可以采用开、闭等基本形态学算法进行平滑(见下图)。之后采用细化操作,将脊线宽度减少到一个像素,产生骨架图像(也叫细化图、脊线图)。当脊线增强效果比较好的时候,通用的形态学算法就可以得到不错的细化图,不过也有研究者针对指纹做了些特殊设计(详见Handbook对应章节)。

从二值图像的脊和谷中消除小洞的结果。输入图像在左侧,输出显示在右侧。通过计算图像的连通成分并删除面积小于给定阈值的成分。
然后扫描细化图的逐个像素,计算其交叉数(crossing number,cn),判断是否为细节点及其类型(结束点或者分叉点)。交叉数
c
n
(
p
)
cn(\textbf{p})
cn(p)的定义为为
p
\textbf{p}
p的八邻域中相邻像素对之间差值的一半(Arcelli和Baja,1984):
c
n
(
p
)
=
1
2
∑
i
=
1
…
8
∣
v
a
l
(
p
i
mod
8
)
−
v
a
l
(
p
i
−
1
)
∣
,
cn\left( {{\textbf{p}}} \right) = \frac{1}{2}\sum_{i = 1 \ldots 8} {\left| {val\left( {{{\textbf{p}}}_{i\,{\text{mod}}\,8} } \right) - val\left( {{{\textbf{p}}}_{i - 1} } \right)} \right|} ,
cn(p)=21i=1…8∑∣val(pimod8)−val(pi−1)∣,这里
p
i
\textbf{p}_i
pi是顺时针排列的八邻域像素,
v
a
l
(
⋅
)
val(\cdot)
val(⋅)为像素值。
对于一个黑色像素(val为1),交叉数有四种情况(见下图):
- 中间点的交叉数为2;
- 结束点的交叉数为1;
- 分叉点的交叉数为3;
- 罕见情况下,交叉数为4。

脊线的中间点、结束点和分叉点的交叉数(crossing number)
确定细节点方向的一种方法如下。对于结束点A,从A出发沿着脊线跟踪固定长度得到另一个点B,然后计算AB连线的角度。对于分叉点A,从A出发沿着分叉后的两条脊线分别跟踪固定长度得到两个点B和C,然后计算两个连线AB和AC的中间角。
8.2 从灰度图像检测
Maio和Maltoni(1997)提出了一种直接从灰度图提取细节点的技术,其基本思想是根据指纹的局部方向跟踪脊线。从数学角度来看,脊线被定义为一组点,这些点是沿一个方向的局部最大值。脊线提取算法尝试在每一步定位相对于与脊线方向正交的截面的局部最大值。通过连接连续的最大值,可以获得脊线的多边形近似。

Maio和Maltoni(1997)的脊线跟踪方法示意图。右侧显示了某些横断面。
Nilsson和Bigun(2001)使用可分离的高斯滤波器和高斯导数滤波器计算线性对称(LS)性质(Bigun和Granlund,1987)。在灰度图像中,细节点被标识为缺乏对称性的点。事实上,虽然非细节点的特征在于一个方向(即细节点角度),沿着这个方向,无穷小的平移使模式的变体最小,但细节点是LS向量场中的局部不连续点。Fronthaler等人(2008a)使用线性对称(LS)和抛物线对称(PS)来检测细节点。在细节点附近,对抛物线对称滤波器的响应较高,而对线性对称滤波器的响应较低。因此,表达式
PS
(
1
−
∣
LS
∣
)
\text{PS}(1 − |\text{LS}|)
PS(1−∣LS∣)比单独的PS或LS能更可靠地检测细节点。下图显示了一个示例。

将Fronthaler等人(2008a)提出的细节点检测方法应用于指纹图像(d)。(a)线性对称性(
LS
\text{LS}
LS),(b)抛物线对称性(
PS
\text{PS}
PS),(c)
PS
(
1
−
∣
LS
∣
)
\text{PS}(1 − |\text{LS}|)
PS(1−∣LS∣),(d)(c)检测图c的局部极大值作为细节点(并进行过滤),叠加到原始指纹图像上。
Larkin和Fletcher(2007)指出细节点对应于相位图的螺旋相位,可以通过环路积分从相位图检测。还有几篇论文采用了类似的细节点检测方法(Gao等,2012;Liu和Cao,2016)。下图的6个例子直观解释了环路积分与细节点数量、极性的关系。

在6幅合成的局部指纹图像中计算曲线积分(红色圆圈表示积分路径)。积分值分别为0,
−
2
π
-2\pi
−2π,
2
π
2\pi
2π,0,
−
4
π
-4\pi
−4π,
4
π
4\pi
4π。(Liu和Cao,2016)
8.3 细节点过滤
许多细节点检测方法仅仅考虑很小的邻域,在低质量指纹区域难免检测到许多虚假细节点。这对于指纹匹配是很不利的。为此,需要细节点过滤步骤(也叫后处理),通过分析细节点周围较大的邻域信息,把伪细节点排除掉。一些技术基于深度网络的细节点检测方法本身已经利用了较大邻域的信息,并不需要额外的过滤步骤。已有的细节点过滤可以分为两类:基于规则的方法和基于学习的方法。
8.3.1 基于规则的细节点过滤
Xiao和Raafat(1991)分析了一些最常见的伪细节点结构,并提出了经验方法去除它们(下图)。他们的算法是基于规则的,需要一些与细节点相关的数值特征作为输入:相关脊线的长度、细节点角度以及邻域中面向细节点的数量等。Bian等人(2002)描述了另外一些用于过滤伪细节点的规则。这类方法可以在删除细节点的同时,完成细化图的修复。

最常见的伪细节点结构(上行)及其去除引起的结构变化(底行)
8.3.2 基于学习的细节点过滤
Maio和Maltoni(1998b)提取原始灰度图像中的细节点邻域,将它们的角度和局部脊线频率进行归一化(见下图),然后传给一个三层神经网络分类器将它们分类为结束点、分叉点或者非细节点。为了利用结束点和分叉点的对偶性,原始邻域及其反色图都输入神经网络分类器。此外,还通过Karhunen-Loeve变换降低邻域的维数,以降低网络的复杂度。实验结果表明,尽管这种过滤方法会遗漏一些真实细节点,但显著减少了伪细节点和细节点类型错误。

Maio和Maltoni(1998b)提取原始灰度图像中的细节点邻域,将它们的角度和局部脊线频率进行归一化。上为结束点,下为分叉点。
许多深度学习细节点检测方法可用于基于灰度图像的细节点过滤,尤其是:
- 基于图像块的分类器(Sankaran等,2014;Jiang等,2016;Darlow和Rosman,2017)可直接用于细节点过滤,而无需滑动窗口扫描;
- 在两阶段方法中(Tang等,2017b;Nguyen等,2018b),第二阶段可以被认为是细节点过滤。
8.4 评测
由于细节点提取是一个很关键的指纹处理步骤,因此单独对其进行测试(而不是将其嵌入整个指纹识别系统)对于评估现有技术的性能和指导未来的发展是非常有用的。主要的障碍是需要真实细节点。手动标记不仅枯燥且容易出错,尤其是标注真正需要重视的低质量指纹。合成指纹可能是一种有意义的策略,可以很方便获得可靠的标注,并适用于低质量数据。
一些研究已在公开数据集上对于几种细节点检测方法进行了测试:
- Kayaoglu等人(2013)使用GUI工具在四个FVC数据集(使用光学、电容和热传感器获取)上手动标记了总共116000个细节点。在相关的指纹识别准确性方面,将商业细节点提取器与手动提取细节点进行比较,得出的结论是,手动提取可以显着提高性能,尤其是在低质量指纹上。
- Chugh等人(2017)将上述四个标记的FVC数据集与NIST SD27结合使用。SD27数据集由257个滚动指纹组成,其细节点由专家标注。该测试还包括合成的指纹库。在缺失和虚假细节点方面,对于三种商业算法和一个开源解决方案(NIST的mindtct)进行了比较。
- Grosz 等人(2020 年)研究不同类型的细节点检测错误对于匹配算法的影响。他们发现,非线性变形和缺失细节点对于指纹细节点匹配器的性能影响,比伪细节点和细节点位置偏移的影响大。
9、三级特征提取
指纹的三级特征包括脊线上的汗孔、脊线外轮廓、点(dot,单个脊线单元)、早期脊线(不成熟脊线,incipient ridge)、皱褶等。这方面的文献较少,实际应用也不多,故此合并为一节。由于实际图像中三级特征的不稳定性,不同研究者对于三级特征采取了相反的态度。一类试图提取三级特征,设计三级特征匹配算法,以提高匹配性能(Jain等,2007)。另一类则是压制三级特征,避免其对于指纹匹配的负面影响(Hara,2011a)。目前还没有合适的数据库和评测,以对比各种方法。
9.1 汗孔
给定足够高分辨率的指纹图像(例如,1000 dpi),可以使用多种技术进行自动汗孔提取:骨架图分析(Stosz和Alyea,1994)、滤波(Jain等,2007)、深度网络(Donida Labati等,2018)。Ding等人(2021)设计了基于U-Net的网络从OCT图像提取汗孔和汗管。
虽然有时候汗孔对于指纹鉴定人员来说非常独特且极其重要,但它们在改进自动指纹识别算法方面的实际效用值得怀疑(Zhang和Jain,2010)。注意到脊线上一串连通的汗孔可能导致脊线被错误地提取为两条脊线,Hara(2011a)提出了一种算法来提取然后消除汗孔以避免此类问题。

Jain等人(2007)的汗孔提取方法
9.2 皱褶
一些指纹(尤其是老年人的)存在大量皱褶。虽然皱褶具有一定的短期稳定性,但是大多数指纹系统被设计为长期工作、且不能进行模板更新,因此大多数关于皱褶的研究是为了去除皱褶。皱褶会对方向场图像的计算产生不利影响,并可能导致检测到错误的脊线结束点。虽然当脊线方向场正确时,上下文滤波技术通常能够填充小皱褶产生的间隙;但是,如果皱褶非常密集或太宽,则上下文滤波仍然有可能失效。为此,研究者提出了明确检测并去除皱褶的方法。
- Vernon(1993)认为皱褶的特征是导致多条脊线的共线结束点,因此利用霍夫变换检测共线结束点以提取皱褶。
- Wu等人(2003)和Zhou等人(2004)使用参数化矩形对皱褶进行建模,然后使用多通道滤波来检测不同方向的皱褶。作者还利用主成分分析估计皱褶的方向、长度和宽度。下图显示了皱褶检测的两个示例。

Wu等人(2003)皱褶检测的两个例子
- Oliveira和Leite(2008)通过观察在两个不同尺度上计算的局部方向场之间的不一致来识别皱褶点。事实上,当以精细尺度计算时,皱褶内的局部脊线方向明显偏离了粗尺度估计的脊线方向。然后提出一种基于分水岭变换的皱褶去除方法。
- Zhou等人(2009b)设计了一种形状为二阶高斯导数的最佳皱褶检测滤波器。除了使用检测到的皱褶来过滤附近的虚假细节点外,作者还表明,将皱褶作为特征与细节点结合使用可以改善老年人的指纹识别准确率。Khan等人(2016)使用了类似的高斯导数滤波器检测皱褶,并利用局部方向引导的修复过程填充皱褶。
- Gottschlich等人(2009)提出了一种面向局部的皱褶检测方法,该方法在二值化图像上追踪脊线和谷线。通过跟踪平行线组以确定局部脊线方向。虽然在皱褶上也可以检测到轨迹,但与脊线相比,这里的平行线数量很少,因此很容易区分皱褶。
10、质量估计
指纹图像质量的含义不同于普通图像质量。指纹图像质量通常与特征的可信度或者匹配性能直接相关。
指纹质量可以在局部级别(为图像的每个块/像素估计不同的值)或全局级别(为整个图像导出单个质量值)进行估计。局部质量图通常与局部特征的可信度有关,而全局质量分数往往直接反应匹配性能。估计指纹质量在实际中有以下用途(Grother和Tabassi,2007):
- 在注册期间,拒绝低质量的图像,让用户再次采集;或者从一组图像中选择质量最佳的图像进行注册;
- 在特征提取环节,根据局部质量图,在不同区域使用适合的特征提取算法。
- 在匹配环节,根据全局质量,采用适合的匹配算法;
- 在匹配环节,根据局部质量图,对于其中的特征采取相应的权重。
估计指纹全局质量的最流行方法是NFIQ(NIST指纹图像质量)。NFIQ的第一个版本可以追溯到2004年(Tabassi等,2004),第二个版本称为NFIQ 2.0,是在十年后推出的(Tabassi等,2021)。NFIQ将全局质量定义为对匹配器性能的预测:高质量的指纹可能会产生较高的匹配分数。这种定义的一大优点是它不需要人类专家提供质量真值,而只需要准备指纹数据库和匹配器。实际上,人工定义质量真值是相当复杂的,无法排除主观意见,而且当质量是为自动匹配算法服务时,人工定义的质量更不是最佳的。
NFIQ和NFIQ 2.0是为基于光学采集仪或卡片扫描的500 dpi的平面和滚动指纹图像而设计的。对于其他类别的传感器,需要进行一些调整(至少是重新训练和校准)。Young和Elliott(2007)的研究表明,平均而言,(1)来自食指和中指的指纹图像比从无名指和小指的图像质量更好,以及(2)斗型纹相比其他纹型的质量高,而弓型纹质量较差。
下面简要总结了用于估计指纹全局和局部质量的方法。Alonso-Fernandez等人(2007)和Yao等人(2018)的综述论文总结了许多指纹质量估计方法。
10.1 局部质量
研究者已经提出了许多方法来估计指纹质量图,其中大多数是根据局部方向可靠性估计,包括Shen等人(2001),Lim等人(2002),Chen等人(2004a),Yao等人(2004),Chen等人(2005),Zhu等人(2005)和Panetta等人(2019)。方向可靠性的定义取决于方向计算方法,但通常与给定邻域中一组方向估计的相干性有关。尽管方向一致性是衡量质量的一个非常强大的特征,但它在奇异点附近无效(奇异点的特点是方向场一致性低)。Fronthaler等人(2006,2008a,b)利用线性和抛物线对称运算符部分克服了这个问题。作者发现,高质量区域中的方向场要么对线性对称滤波器的响应高(远离奇异点),要么对抛物线对称滤波器的响应高(奇异点附近),而低质量区域的方向场对于两种滤波器的响应都比较弱。
其他特征可用于表征局部质量:
- 从像素灰度得出的统计数据(例如,平均值、方差、对比度、梯度幅度、直方图特征等),例如Shi等人(2004)、Uchida(2004)、Chen等人(2004b)、Lim等人(2004)、Hwang(2004)、Qi等人(2005a)、Zhu等人(2005)。
- 脊线频率、脊线宽度和脊到谷宽度(Lim等人,2002 年;朱等, 2005);如果这些值与其典型值偏差很大,则说明是质量不好的区域。
- 局部区域的傅里叶频谱中是否存在主导频率(Lim等人,2004)以及空间域与理想正弦波图案的局部相似性(Lee等人,2006)。
- 邻近指纹块对应的流形的规律性(Tao等人,2012)。
Liu等人(2020)对大量指纹块进行了聚类分析,将它们分为四个质量类(并增加了背景和奇异点区域),然后训练了一个简单的神经网络分类器,根据经验定义的特征向量进行块分类。
由于质量定义不统一,很难定量比较这些方法的相对性能。在ANSI/NIST-ITL 1-2011(2015)标准中,指纹的局部质量(分为六个级别)是根据不同级别特征的可靠性定义的。但是,没有基于此标准的公开指纹数据库用于科学研究。
10.2 全局质量
Qi等人(2005b)对文献中已有的局部和全局特征进行了综合,在全局特征方面,作者建议考虑前景区域的大小,前景相对于图像中心是否居中,以及是否存在可检测的奇异点。
高质量的指纹图像在傅里叶频谱的原点周围表现为一个环。原因是指纹的脊线图案是准周期结构,并且在大多数方向的主频率上幅度相似。Uchida(2004)、Chen等人(2005)和Lee等人(2005)利用经验设计的环形检测器从频谱图估计指纹全局质量。
Munir等人(2012)、Sharma和Dey(2019)利用分层或模糊聚类将指纹分组到不同的质量等级,尤其是推断指纹的干湿程度。
Yao等人(2015)的质量度量仅依赖于细节点,可以根据标准模板(例如,ISO标准格式)计算,而无需原始指纹图像。为了计算质量,作者使用凸包和Delaunay三角对细节点集进行建模。作者观察到,由于存在虚假细节点,低质量指纹会产生又小又窄的三角形(高质量指纹不常见)。因此,他们使用细节点三角形的几何表征来确定质量。Yao等人(2018)的实验表明,尽管这种方法很简单,但在用于选择最佳样本进行注册时非常有效。
两个指纹重叠区域的大小对匹配性能有很大影响。为了保证较大的重叠区域,在注册和识别阶段首选采集指纹的中心区域。因此,具有大中心区域的指纹应比具有相似图像质量和整体大小但中心区域较小的指纹分配更高的质量。考虑到这一因素,Hara(2011b)提出根据中心区域(称为模式区域)的完整性和该区域的脊线质量来估计指纹质量。
为了评估全局质量估计方法的有效性,Grother和Tabassi(2007)提出测量拒绝低质量指纹带来的匹配准确率提升程度。为此,可以绘制FNMR与拒绝率的曲线(见下图),更接近原点的曲线表示更有效的质量估计算法。如果质量估计需要独立于特定的指纹识别算法(例如一些大规模政府指纹项目可能需要允许多种识别算法入选),在定义和估计质量时,应考虑混合使用多种指纹特征提取和匹配技术。

随着提高拒绝阈值(拒绝低于质量阈值的指纹),真匹配被拒绝的比例升高,而FNMR下降。在相同的拒绝比例下,FNMR越低说明质量估计越有效。(Tabassi等,2021)
10.3 NFIQ(NIST指纹图像质量)
10.3.1 NFIQ 1.0
指纹图像
x
i
x_i
xi的质量
q
(
x
i
)
q(x_i)
q(xi)定义为对归一化匹配分数
n
o
r
m
s
c
o
r
e
(
x
i
)
normscore( {x_i } )
normscore(xi) 的预测。设
T
T
T是一个训练集,其中包含
n
n
n个手指,每个手指
i
=
1
,
.
.
.
,
n
i = 1,..., n
i=1,...,n有一对指纹
(
x
i
,
x
i
′
)
(x_i ,x_i')
(xi,xi′) 。
x
i
x_i
xi的归一化匹配分数是根据
x
i
x_i
xi的真匹配分数与
x
i
x_i
xi的假匹配分数的分离程度来定义的:
n
o
r
m
s
c
o
r
e
(
x
i
)
=
s
c
o
r
e
(
x
i
,
x
i
′
)
−
avg
j
=
1...
n
,
j
≠
i
(
s
c
o
r
e
(
x
i
,
x
j
)
)
stdev
j
=
1...
n
,
j
≠
i
(
s
c
o
r
e
(
x
i
,
x
j
)
)
,
normscore( {x_i } ) = \frac{{score ( {x_i ,x_i' } ) - {\text{avg}}_{j = 1 ... n,j \ne i} \left( {score\left( {x_i ,x_j } \right)} \right)}}{{{\text{stdev}}_{j = 1 ... n,j \ne i} \left( {score\left( {x_i ,x_j } \right)} \right)}},
normscore(xi)=stdevj=1...n,j=i(score(xi,xj))score(xi,xi′)−avgj=1...n,j=i(score(xi,xj)),其中
s
c
o
r
e
(
a
,
b
)
score(a,b)
score(a,b)是匹配器关于两个指纹
a
a
a和
b
b
b之间的匹配分数,
avg
(
)
\text{avg}()
avg() 是平均值,
stdev
(
)
\text{stdev}()
stdev() 是标准偏差。
给定从
x
i
x_i
xi提取的特征向量
v
i
v_i
vi,对训练集
T
T
T上的样本对
<
v
i
,
n
o
r
m
s
c
o
r
e
(
x
i
)
>
,
i
=
1...
n
<v_i,normscore(x_i)>, i = 1...n
<vi,normscore(xi)>,i=1...n进行回归,可以得到
v
i
v_i
vi和
q
(
x
i
)
q(x_i)
q(xi)之间的映射。Tabassi等人(2004)将回归问题转化为分类问题,将指纹质量量化为五个离散值。为此,训练神经网络分类器将特征向量分类为五个预定义的质量类之一(其中类一表示最高质量,类五表示最差质量)。每个特征向量由11个特征组成。为了提取这些特征,该方法根据局部方向、局部对比度和曲率的一致性计算前景质量图。然后执行细节点检测,并根据细节点附近的像素灰度统计量(平均值和标准偏差)计算每个细节点的可靠性。然后将细节点的可靠性与细节点处的局部质量(来自质量图)相结合,得到每个细节点的质量。
10.3.2 NFIQ 2.0
Tabassi等人(2021)描述的NFIQ 2.0是NFIQ的升级版。在开发NFIQ 2.0过程中,作者考虑的主要因素是:更高的效率,更精细的粒度(101个质量级别而不是5个)和模块化设计。通过全面的文献调研,作者选择了155个候选特征;然后根据预测能力、计算时间成本和相关性选择了14个特征(见表3.2);最后使用随机森林分类器根据特征向量预测指纹质量。
Tabassi等人(2013)提出了NFIQ 2.0的精简版。此方法基于Bag-of-Words 方法,可以在低配准客户端上高效运行。作者从许多指纹图像中提取了大量训练块(24×24像素),通过聚类形成码本(也叫视觉词典)。给定码本,通过以下步骤从指纹提取定长向量:(1)将图像分块;(2)在码本中搜索每个块的最相似码字,(3)构建码字的直方图。然后训练随机森林分类器以将特征向量映射到质量级。
11、总结
指纹特征提取算法的设计曾经非常依赖经验。沿着这条路线,技术很难进步。在过去十年中,机器学习方法逐渐被应用于指纹特征提取算法,最初是基于字典方法,近来更多依赖于流行的深度学习模型。融合深度学习模型和领域知识的技术已经能够实现现场指纹的全自动处理(包括前景分割和细节点提取),对于较高质量现场指纹的识别性能接近甚至超过手工标注的性能。不过,对于极低质量的指纹图像,当前算法的准确性和效率方面还可以进一步提高。
在指纹特征提取的许多任务上,深度学习方法的准确性通常要优于传统方法,但GPU平台的成本高、体积大,无法用于许多应用。在基于嵌入式设备的指纹识别系统中,传统方法仍然是必要的。
参考文献
- Abhyankar, A., & Schuckers, S. (2010). Towards integrating level-3 features with perspiration pattern for robust fingerprint recognition. In 2010 IEEE International Conference on Image Processing (pp. 3085–3088).
- Almansa, A., & Lindeberg, T. (1997). Enhancement of fingerprint images using shape-adapted scale-space operators. In J. Sporring, M. Nielsen, L. Florack & P. Johansen (Eds.), Gaussian Scale-space Theory (pp. 21–30). Kluwer.
- Almansa, A., & Lindeberg, T. (2000). Fingerprint enhancement by shape adaptation of scale-space operators with automatic scale selection. IEEE Transactions on Image Processing, 9(12), 2027–2042.
- Alonso-Fernandez, F., Fierrez-Aguilar, J., & Ortega-Garcia, J. (2005). An enhanced Gabor filter-based segmentation algorithm for fingerprint recognition systems. In Proceedings of International Symposium on Image and Signal Processing and Analysis.
- Alonso-Fernandez, F., Fierrez, J., Ortega-Garcia, J., Gonzalez-Rodriguez, J., Fronthaler, H., Kollreider, K., & Bigun, J. (2007). A comparative study of fingerprint image-quality estimation methods. IEEE Transactions on Information Forensics and Security, 2(4), 734–743.
- Anand, V., & Kanhangad, V. (2019). Pore detection in high-resolution fingerprint images using deep residual network. Journal of Electronic Imaging, 28(2), 020502.
- ANSI/INCITS. (2004). INCITS 378-2004—Finger minutiae format for data interchange. ANSI/INCITS standard.
- ANSI/NIST—CDEFFS group. (2008). Data format for the interchange of extended fingerprint and palmprint features—Addendum to ANSI/NIST–ITL 1–2007. ANSI/NIST, Working Draft 0.2.
- Araque, J. L., Baena, M., Chalela, B. E., Navarro, D., & Vizcaya P. R. (2002). Synthesis of fingerprint images. In Proceedings of 16th International Conference on Pattern Recognition (Vol. 2, pp. 442–445).
- Arcelli, C., & Baja, G. S. D. (1984). A width independent fast thinning algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligence, 4(7), 463–474.
- Areekul, V., Watchareeruetai, U., Suppasriwasuseth, K., & Tantaratana, S. (2005). Separable Gabor filter realization for fast fingerprint enhancement. In Proceedings of International Conference on Image Processing (Vol. 3, pp. 253–256).
- Areekul, V., Suppasriwasuseth, K., & Jirachawang, S. (2006). The new focal point localization algorithm for fingerprint registration. In Proceedings of 18th International Conference on Pattern Recognition (Vol. 4, pp. 497–500).
- Ashbaugh, D. R. (1999). Quantitative–qualitative friction ridge analysis: An introduction to basic and advanced ridgeology. CRC Press.
- Aujol, J. F., Gilboa, G., Chan, T., & Osher, S. (2006). Structure-texture image decomposition-modeling, algorithms, and parameter selection. International Journal of Computer Vision, 67, 111–136.
- Ballard, D. H. (1981). Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognition, 3(2), 110–122.
- Bartunek, J. S., Nilsson, M., Sallberg, B., & Claesson, I. (2013). Adaptive fingerprint image enhancement with emphasis on preprocessing of data. IEEE Transactions on Image Processing, 22(2), 644–656.
- Baruch, O. (1988). Line thinning by line following. Pattern Recognition Letters, 8(4), 271–276.
- Bazen, A. M., & Gerez, S. H. (2001). Segmentation of fingerprint images. In Proceedings of Workshop on Circuits Systems and Signal Processing.
- Bazen, A. M., & Gerez, S. H. (2002). Systematic methods for the computation of the directional fields and singular points of fingerprints. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(7), 905–919.
- Bazin, A. I., & Mansfield, T. (2007). An investigation of minutiae template interoperability. In Proceedings of Workshop on Automatic Identification Advanced Technologies (pp. 13–18).
- Bernard, S., Boujemaa, N., Vitale, D., & Bricot, C. (2002). Fingerprint segmentation using the phase of multiscale Gabor wavelets. In Proceedings of Asian Conference Computer Vision.
- Bhanu, B., Boshra, M., & Tan, X. (2000). Logical templates for feature extraction in fingerprint images. In Proceedings of 15th International Conference on Pattern Recognition (Vol. 2, pp. 850–854).
- Bhanu, B., & Tan, X. (2001). Learned templates for feature extraction in fingerprint images. In Proceedings of Conference on Computer Vision and Pattern Recognition (Vol. 2, pp. 591–596).
- Bhowmick, P., Bishnu, A., Bhattacharya, B. B., Kundu, M. K., Murthy, C. A., & Acharya, T. (2002). Determination of minutiae scores for fingerprint image applications. In Proceedings of Indian Conference on Computer Vision Graphics Image Processing (pp. 463–468).
- Bhowmick, P., & Bhattacharya, B. B. (2009). Removal of digitization errors in fingerprint ridgelines using B-splines. Pattern Recognition, 42(3), 465–474.
- Bian, W., Luo, Y., Xu, D., & Yu, Q. (2014). Fingerprint ridge orientation field reconstruction using the best quadratic approximation by orthogonal polynomials in two discrete variables. Pattern Recognition, 47(10), 3304–3313.
- Bian, W., Ding, S., & Xue, Y. (2017a). Combining weighted linear project analysis with orientation diffusion for fingerprint orientation field reconstruction. Information Sciences, 396, 55–71.
- Bian, W., Ding, S., & Xue, Y. (2017b). Fingerprint image super resolution using sparse representation with ridge pattern prior by classification coupled dictionaries. IET Biometrics, 6(5), 342–350.
- Bian, W., Ding, S., & Jia, W. (2018). Collaborative filtering model for enhancing fingerprint image. IET Image Processing, 12(1), 149–157.
- Bian, W., Xu, D., Li, Q., Cheng, Y., Jie, B., & Ding, X. (2019). A survey of the methods on fingerprint orientation field estimation. IEEE Access, 7, 32644–32663.
- Bian, Z., Zhang, D., & Shu, W. (2002). Knowledge-based fingerprint post-processing. International journal of pattern recognition and artificial intelligence, 16(01), 53-67.
- Bigun, J., & Granlund, G. H. (1987). Optimal orientation detection of linear symmetry. In Proceedings of 1st International Conference on Computer Vision (pp. 433–438).
- Bolle, R., Serior, A. W., Ratha, N. K., & Pankanti, S. (2002). Fingerprint minutiae: A constructive definition. In Proceedings of ECCV Workshop on Biometric Authentication (pp. 58–66).
- Branka, S., Marques, O., & Nešković, A. (2019). Segmentation and separation of overlapped latent fingerprints: Algorithms, techniques, and datasets. Briefs in Computer Science. Springer.
- Buades, A., Le, T. M., Morel, J., & Vese, L. A. (2010). Fast cartoon + texture image filters. IEEE Transactions on Image Processing, 19(8), 1978–1986.
- Can, X., & Lin, Y. (2009). An adaptive algorithm for smoothing fingerprint orientation fields. In Proceedings of International Conference on Computational Intelligence and Natural Computing, Wuhan, China (pp. 70–72).
- Canyellas, N., Cantó, E., Forte, G., &, López, M. (2005). Hardware–software codesign of a fingerprint identification algorithm. In Proceedings of 5th International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 683–692).
- Cao, K., & Jain, A. K. (2015). Latent orientation field estimation via convolutional neural network. In Proceedings of International Conference on Biometrics (ICB), Phuket, Thailand.
- Cao, K., Liang, J., & Tian, J. (2012). A div-curl regularization model for fingerprint orientation extraction. In Proceedings of International Conference on Biometrics: Theory, Applications and Systems, Arlington, VA (pp. 231–236).
- Cao, K., Liu, E., & Jain, A. K. (2014). Segmentation and enhancement of latent fingerprints: A coarse to fine ridge structure dictionary. IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(9), 1847–1859.
- Cappelli, R., & Maltoni, D. (2009). On the spatial distribution of fingerprint singularities. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(4), 742–748.
- Cappelli, R., Maio, D., & Maltoni, D. (1999). Fingerprint classification based on multi-space KL. In Proceedings of Workshop on Automatic Identification Advances Technologies (pp. 117–120).
- Cappelli, R., Maio, D., & Maltoni, D. (2000). Synthetic fingerprint-image generation. In Proceedings of 15th International Conference on Pattern Recognition (Vol. 3, pp. 475–478).
- Cappelli, R., Maio, D., & Maltoni, D. (2009). Semi-automatic enhancement of very low quality fingerprints. In Proceedings of International Symposium on Image and Signal Processing and Analysis, Salzburg (pp. 678–683).
- Cappelli, R., Maltoni, D., & Turroni, F. (2012). Fingerprint enhancement using contextual iterative filtering. In Proceedings International Conference on Biometrics (ICB), New Delhi, India.
- Champod, C., Lennard, C. J., Margot, P., & Stoilovic, M. (2016). Fingerprints and Other Ridge Skin Impressions (2nd ed.). CRC Press.
- Chang, J. H., & Fan, K. C. (2001). Fingerprint ridge allocation in direct gray-scale domain. Pattern Recognition, 34(10), 1907–1925.
- Chen, T., Jiang, X., & Yau, W. (2004a). Fingerprint image quality analysis. In Proceedings of International Conference on Image Processing (pp. 1253–1256).
- Chen, X., Tian, J., Cheng, J., & Yang, X. (2004b). Segmentation of fingerprint images using linear classifier. EURASIP Journal on Applied Signal Processing, 2004(4), 480–494.
- Chen, Y., Dass, S. C., & Jain, A. K. (2005). Fingerprint quality indices for predicting authentication performance. In Proceedings of 5th International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 160–170).
- Chen, J., Chan, F., & Moon, Y. S. (2007). Fingerprint matching with minutiae quality score. In Proceedings of International Conference on Biometrics (pp. 663–672).
- Chen, F., Feng, J., Jain, A. K., Zhou, J., & Zhang, J. (2011a). Separating overlapped fingerprints. IEEE Transactions on Information Forensics and Security, 6(2), 346–359.
- Chen, H., Pang, L., Liang, J., Liu, E., & Tian, J. (2011b). Fingerprint singular point detection based on multiple-scale orientation entropy. IEEE Signal Processing Letters, 18(11), 679–682.
- Chen, C., Feng, J., & Zhou, J. (2016). Multi-scale dictionaries based fingerprint orientation field estimation. In Proceedings of International Conference on Biometrics (pp. 1–8).
- Cheng, J., & Tian, J. (2004). Fingerprint enhancement with dyadic scale-space. Pattern Recognition Letters, 25(11), 1273–1284.
- Chikkerur, S., & Ratha, N. (2005). Impact of singular point detection on fingerprint matching performance. In Proceedings of Workshop on Automatic Identification Advanced Technologies (pp. 207–212).
- Chikkerur, S., Govindaraju, V., Pankanti, S., Bolle, R., & Ratha, N. (2005). Novel approaches for minutiae verification in fingerprint images. In Proceedings of Workshops on Application of Computer Vision (Vol. 1, pp. 111–116).
- Chikkerur, S., Cartwright, A. N., & Govindaraju, V. (2007). Fingerprint enhancement using STFT analysis. Pattern Recognition, 40(1), 198–211.
- Chugh, T., Arora, S. S., Jain, A. K., & Paulter, N. G. (2017). Benchmarking fingerprint minutiae extractors. In Proceedings of International Conference of the Biometrics Special Interest Group.
- Coetzee, L., & Botha, E. C. (1993). Fingerprint recognition in low quality images. Pattern Recognition, 26(10), 1441–1460.
- Da Costa, J. P., Le Pouliquen, F., Germain, C., & Baylou, P. (2001). New operators for optimized orientation estimation. In Proceedings of International Conference on Image Processing.
- Darlow, L. N., & Rosman, B. (2017). Fingerprint minutiae extraction using deep learning. In Proceedings of International Joint Conference on Biometrics, Denver, CO (pp. 22–30).
- Dass, S. C. (2004). Markov random field models for directional field and singularity extraction in fingerprint images. IEEE Transactions on Image Processing, 13(10), 1358–1367.
- Daugman, J. G. (1985). Uncertainty relation for resolution in space, spatial-frequency, and orientation optimized by two-dimensional visual cortical filters. Journal Optical Society American, 2, 1160–1169.
- Deerada, C., Phromsuthirak, K., Rungchokanun, A., & Areekul, V. (2020). Progressive focusing algorithm for reliable pose estimation of latent fingerprints. IEEE Transactions on Information Forensics and Security, 15, 1232–1247.
- Ding, B., Wang, H., Chen, P., Zhang, Y., Guo, Z., Feng, J., & Liang, R. (2021). Surface and internal fingerprint reconstruction from optical coherence tomography through convolutional neural network. IEEE Transactions on Information Forensics and Security, 16, 685–700.
- Donahue, M. L., & Rokhlin, S. I. (1993). On the use of level curves in image analysis. CVGIP: Image Understanding, 57(2), 185–203.
- Donida Labati, R., Genovese, A., Muñoz, E., Piuri, V., & Scotti, F. (2018). A novel pore extraction method for heterogeneous fingerprint images using convolutional neural networks. Pattern Recognition Letters, 113, 58–66.
- Duda, R. O., Hart, P. E., & Stork, D. G. (2000). Pattern classification, 2nd edn. Wiley.
- Erol, A., Halici, U., & Ongun, G. (1999). Feature selective filtering for ridge extraction. In L.C. Jain, U. Halici, I. Hayashi & S.B. Lee (Eds.), Intelligent biometric techniques in fingerprint & face recognition. CRC Press.
- Ezeobiejesi, J., & Bhanu, B. (2017). Latent fingerprint image segmentation using deep neural network. In B. Bhanu & A. Kumar (Eds.), Deep learning for biometrics. Springer.
- Fan, L., Wang, S., Wang, H., & Guo, T. (2008). Singular points detection based on zero-pole model in fingerprint images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30(6), 929–940.
- Farina, A., Kovacs-Vajna, Z. M., Leone, A. (1999). Fingerprint minutiae extraction from skeletonized binary images. Pattern Recognition, 32(5), 877–889.
- Feng, J., Shi, Y., & Zhou, J. (2012). Robust and efficient algorithms for separating latent overlapped fingerprints. IEEE Transactions on Information Forensics and Security, 7(5), 1498–1510.
- Feng, J., Zhou, J., & Jain, A. K. (2013). Orientation field estimation for latent fingerprint enhancement. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(4), 925–940.
- Fitz, A. P., & Green, R. J. (1996). Fingerprint classification using hexagonal fast Fourier transform. Pattern Recognition, 29(10), 1587–1597.
- Freeman, W. T., & Adelson, E. H. (1991). The design and use of steerable filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(9), 891–906.
- Fronthaler, H., Kollreider, K., & Bigun, J. (2006). Automatic image quality assessment with application in biometrics. In Proceedings of CVPR Workshop on Biometrcis (pp. 30–35).
- Fronthaler, H., Kollreider, K., & Bigun, J. (2007). Pyramid-based image enhancement of fingerprints. In Proceedings of Workshop on Automatic Identification Advanced Technologies (pp. 45–50).
- Fronthaler, H., Kollreider, K., & Bigun, J. (2008a). Local features for enhancement and minutiae extraction in fingerprints. IEEE Transactions on Image Processing, 17(3), 354–363.
- Fronthaler, H., Kollreider, K., Bigun, J., Fierrez, J., Alonso-Fernandez, F., Ortega-Garcia, J., & Gonzalez-Rodriguez, J. (2008b). Fingerprint image-quality estimation and its application to multialgorithm verification. IEEE Transactions on Information Forensics and Security, 3(2), 331–338.
- Gall, J., & Lempitsky, V. (2013). Class-specific Hough forests for object detection. In A. Criminisi & J. Shotton (Eds.), Decision forests for computer vision and medical image analysis. Springer.
- Galton, F. (1892). Finger prints. Macmillan.
- Gamassi, M., Piuri, V., & Scotti, F. (2005). Fingerprint local analysis for high-performance minutiae extraction. In Proceedings of International Conference on Image Processing (Vol. 3, pp. 265–268).
- Gao, X., Chen, X., Cao, J., Deng, Z., Liu, C., & Feng, J. (2010). A novel method of fingerprint minutiae extraction based on Gabor phase. In 2010 IEEE International Conference on Image Processing (pp. 3077-3080).
- Girshick, R. (2015). Fast R-CNN. In Proceedings of International Conference on Computer Vision (pp. 1440–1448).
- Gonzales, R. C., & Woods, R. E. (2007). Digital image processing, 3rd edn. Prentice-Hall.
- Gottschlich, C. (2012). Curved-region-based ridge frequency estimation and curved gabor filters for fingerprint image enhancement. IEEE Transactions on Image Processing, 21(4), 2220–2227.
- Gottschlich, C., & Schönlieb, C. (2012). Oriented diffusion filtering for enhancing low-quality fingerprint images. IET Biometrics, 1(2), 105–113.
- Gottschlich, C., Mihailescu, P., & Munk, A. (2009). Robust orientation field estimation and extrapolation using semilocal line sensors. IEEE Transactions on Information Forensics and Security, 4(4), 802–811.
- Gottschlich, C., Tams, B., & Huckemann, S. (2017). Perfect fingerprint orientation fields by locally adaptive global models. IET Biometrics, 6(3), 183–190.
- Govindaraju, V., Shi, Z., & Schneider, J. (2003). Feature extraction using a chaincoded contour representation of fingerprint images. In Proceedings of 4th International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 268–275.)
- Grasselli, A. (1969). On the automatic classification of fingerprints. In S. Watanabe (Ed.), Methodologies of pattern recognition. Academic.
- Greenberg, S., Aladjem, M., Kogan, D., & Dimitrov, I. (2000). Fingerprint image enhancement using filtering techniques. In Proceedings of 15th International Conference on Pattern Recognition (Vol. 3, pp. 326–329).
- Grosz, S. A., Engelsma, J. J., Paulter, N. G., & Jain, A. K. (2020). White-box evaluation of fingerprint matchers: Robustness to minutiae perturbations. In Proceedings of International Joint Conference on Biometrics (pp. 1–10).
- Grother, P., & Tabassi, E. (2007). Performance of biometric quality measures. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(4), 531–543.
- Grother, P., McCabe, M., Watson, C., Indovina, M., Salamon, W., Flanagan, P., Tabassi, E., Newton, E., & Wilson, C. (2006). Performance and Interoperability of the INCITS 378 Fingerprint Template. NIST Research Report: NISTIR 7296.
- Gu, J., Zhou, J., & Yang, C. (2006). Fingerprint recognition by combining global structure and local cues. IEEE Transactions on Image Processing, 15(7), 1952–1964.
- Gu, S., Feng, J., Lu, J., & Zhou, J. (2018). Efficient rectification of distorted fingerprints. IEEE Transactions on Information Forensics and Security, 13(1), 156–169.
- Hara, M. (2011a). System for recognizing fingerprint image, method and program for the same. US Patent 8019132.
- Hara, M. (2011b). Fingerprint collation apparatus, fingerprint pattern area extracting apparatus and quality judging apparatus, and method and program of the same. US Patent 7885437.
- Hari, V. S., Jagathy Raj, V. P., & Gopikakumari, R. (2013). Unsharp masking using quadratic filter for the enhancement of fingerprints in noisy background. Pattern Recognition, 46(12), 3198–3207.
- He, Y., Tian, J., Luo, X., & Zhang, T. (2003). Image enhancement and minutiae matching in fingerprint verification. Pattern Recognition Letters, 24(9), 1349–1360.
- Henry, E. (1900). Classification and uses of finger prints.
- Hicklin, R. A. (2009). Anatomy of friction ridge skin. In S. Z. Li & A. K. Jain (Eds.), Encyclopedia of biometrics. Springer.
- Hong, L., Jain, A. K., Pankanti, S., & Bolle, R. (1996). Fingerprint enhancement. In Proceedings of Workshop on Applications of Computer Vision (pp. 202–207).
- Hong, L., Wan, Y., & Jain, A. K. (1998). Fingerprint image enhancement: Algorithms and performance evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(8), 777–789.
- Hotz, T. (2009). Intrinsic coordinates for fingerprints based on their longitudinal axis. In Proceedings of International Symposium on Image and Signal Processing and Analysis, Salzburg (pp. 500–504).
- Hou, Z., & Yau, W. (2010). A variational formulation for fingerprint orientation modelling. In Proceedings of International Conference on Pattern Recognition, Istanbul (pp. 1626–1629).
- Hsieh, C. T., Lai, E., & Wang, Y. C. (2003). An effective algorithm for fingerprint image enhancement based on wavelet transform. Pattern Recognition, 36(2), 303–312.
- Huang, C. Y., Liu, L. M., & Hung, D. C. D. (2007). Fingerprint analysis and singular point detection. Pattern Recognition Letters, 28(15), 1937–1945.
- Huckemann, S., Hotz, T., & Munk, A. (2008). Global models for the orientation field of fingerprints: An approach based on quadratic differentials. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30(9), 1507–1519.
- Hung, D. C. D. (1993). Enhancement and feature purification of fingerprint images. Pattern Recognition, 26(11), 1661–1671.
- Hung, D. C. D., & Huang, C. (1996). A model for detecting singular points of a fingerprint. In Proceedings of 9th Florida Artificial Intelligence Research Symposium (pp. 444–448).
- Hwang, K. (2004). Statistical quality assessment of a fingerprint. In Proceedings of SPIE Conference on Biometric Technology for Human Identification I.
- Ikeda, N., Nakanishi, M., Fujii, K., Hatano, T., Shigematsu, S., Adachi, T., Okazaki, Y., & Kyuragi, H. (2002). Fingerprint image enhancement by pixel-parallel processing. In Proceedings of 16th International Conference on Pattern Recognition (Vol. 3, pp. 752–755).
- ISO/IEC 19794-2. (2011). ISO, “ISO/IEC 19794-2:2011 – Information technology – Biometric data interchange formats – Part 2: Finger minutiae data”.
- ISO/IEC 29794-4. (2017). Information technology—Biometric sample quality—Part 4: Finger image data. ISO/IEC Standard.
- Isola, P., Zhu, J., Zhou, T., & Efros, A. A. (2017). Image-to-image translation with conditional adversarial networks. In Proceedings of Conference on Computer Vision and Pattern Recognition (pp. 5967–5976).
- Jain, A. K., & Farrokhnia, F. (1991). Unsupervised texture segmentation using Gabor filters. Pattern Recognition, 24(12), 1167–1186.
- Jain, A. K., Hong, L., Pankanti, S., & Bolle, R. (1997). An identity authentication system using fingerprints. Proceedings of the IEEE, 85(9), 1365–1388.
- Jain, A. K., Prabhakar, S., Hong, L., & Pankanti, S. (2000). Filterbank-based fingerprint matching. IEEE Transactions on Image Processing, 9(5), 846–859.
- Jain, A. K., Chen, Y., & Demirkus, M. (2007). Pores and ridges: High-resolution fingerprint matching using Level 3 features. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(1), 15–27.
- Jang, W., Park, D., Lee, D., & Kim, S. J. (2006). Fingerprint image enhancement based on a half gabor filter. In Proceedings of International Conference on Biometrics (pp. 258–264).
- Jang, H., Kim, D., Mun, S., Choi, S., & Lee, H. (2017). DeepPore: Fingerprint pore extraction using deep convolutional neural networks. Signal Processing Letters, 24(12), 1808–1812.
- Ji, L., & Yi, Z. (2008). Fingerprint orientation field estimation using ridge projection. Pattern Recognition, 41(5), 1508–1520.
- Ji, L., Yi, Z., Shang, L., & Pu, X. (2007). Binary fingerprint image thinning using template-based PCNNs. IEEE Transaction on Systems, Man, and Cybernetics, Part B, 37(5), 1407–1413.
- Jiang, X. (2000). Fingerprint image ridge frequency estimation by higher order spectrum. In Proceedings of International Conference on Image Processing.
- Jiang, X. (2001). A study of fingerprint image filtering. In Proceedings of International Conference on Image Processing.
- Jiang, X., Yau, W. Y., & Ser, W. (1999). Minutiae extraction by adaptive tracing the gray level ridge of the fingerprint image. In Proceedings of International Conference on Image Processing.
- Jiang, X., Yau, W. Y., & Ser, W. (2001). Detecting the fingerprint minutiae by adaptive tracing the gray-level ridge. Pattern Recognition, 34(5), 999–1013.
- Jiang, X., Liu, M., & Kot, A. C. (2004). Reference point detection for fingerprint recognition. In Proceedings of 17th International Conference on Pattern Recognition (Vol. 1, pp. 540–543).
- Jiang, L., Zhao, T., Bai, C., Yong, A., & Wu, M. (2016). A direct fingerprint minutiae extraction approach based on convolutional neural networks. In Proceedings of International Joint Conference on Neural Networks, Vancouver, BC (pp. 571–578).
- Jirachaweng, S., & Areekul, V. (2007). Fingerprint enhancement based on discrete cosine transform. In Proceedings of International Conference on Biometrics (pp. 96–105).
- Jirachaweng, S., Hou, Z., Yau, W. Y., & Areekul, V. (2011). Residual orientation modeling for fingerprint enhancement and singular point detection. Pattern Recognition, 44(2), 431–442.
- Jolliffe, I. T. (1986). Principle component analysis. Springer.
- Joshi, I., Anand, A., Vatsa, M., Singh, R., Roy, S. D., & Kalra, P. (2019). Latent fingerprint enhancement using generative adversarial networks. In Proceedings Winter Conference on Applications of Computer Vision, Waikoloa Village, HI, USA (pp. 895–903).
- Kamei, T. (2004). Image filter design for fingerprint enhancement. In N. Ratha & R. Bolle (Eds.), Automatic fingerprint recognition systems (pp. 113–126). Springer.
- Kamei, T., & Mizoguchi, M. (1995). Image filter design for fingerprint enhancement. In Proceedings of International Symposium on Computer Vision (pp. 109–114).
- Karu, K., & Jain, A. K. (1996). Fingerprint classification. Pattern Recognition, 29(3), 389–404.
- Kass, M., & Witkin, A. (1987). Analyzing oriented patterns. Computer Vision Graphics and Image Processing, 37(3), 362–385.
- Kawagoe, M., & Tojo, A. (1984). Fingerprint pattern classification. Pattern Recognition, 17, 295–303.
- Kayaoglu, M., Topcu, B., & Uludag, U. (2013). Standard fingerprint databases: Manual minutiae labeling and matcher performance analyses. arXiv:1305.1443.
- Khan, M. A. U., Khan, T. M., Bailey, D. G., & Kong, Y. (2016). A spatial domain scar removal strategy for fingerprint image enhancement. Pattern Recognition, 60, 258–274.
- Kim, D. H. (2005). Minutiae quality scoring and filtering using a neighboring ridge structural analysis on a thinned fingerprint image. In Proceedings of 5th International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 674–682).
- Kim, B. G., & Park, D. J. (2002). Adaptive image normalisation based on block processing for enhancement of fingerprint image. Electronics Letters, 38(14), 696–698.
- Kim, S., Lee, D., & Kim, J. (2001). Algorithm for detection and elimination of false minutiae in fingerprint images. In Proceedings of 3rd International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 235–240).
- Kohonen, T., Kangas, J., Laaksonen, J., & Torkkola, K. (1992). LVQ_PAQ: A program package for the correct application of learning vector quantization algorithms. In Proceedings of International Joint Conference On Neural Network (pp. 1725–1730).
- Koo, W. M., & Kot, A. (2001). Curvature-based singular points detection. In Proceedings of 3rd International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 229–234).
- Kovacs-Vajna, Z. M. (2000). A fingerprint verification system based on triangular matching and dynamic time warping. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22, 1266–1276.
- Kovacs-Vajna, Z. M., Rovatti, R., & Frazzoni, M. (2000). Fingerprint ridge distance computation methodologies. Pattern Recognition, 33(1), 69–80.
- Kryszczuk, K., & Drygajlo, A. (2006). Singular point detection in finger-prints using quadrant change information. In Proceedings of 18th International Conference on Pattern Recognition (Vol. 4, pp. 594–597).
- Kryszczuk, K. M., Morier, P., & Drygajlo, A. (2004). Study of the distinctiveness of level 2 and level 3 features in fragmentary fingerprint comparison. In Proceedings of ECCV Workshop on Biometric Authentication (pp. 124–133).
- Lam, L., Lee, S. W., & Suen, C. Y. (1992). Thinning methodologies: A comprehensive survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(9), 869–885.
- Landy, M. S., Cohen, Y., & Sperling, G. (1984). Hips: A Unix-based image processing system. Computer Vision, Graphics and Image Processing, 25(3), 331–347.
- Larkin, K. G. (2005). Uniform estimation of orientation using local and nonlocal 2-D energy operators. Optics Express, 13(20), 8097–8121.
- Larkin, K. G., & Fletcher, P. A. (2007). A coherent framework for fingerprint analysis: Are fingerprints holograms? Optics Express, 15(14), 8667–8677.
- Le, T. H., & Van, H. T. (2012). Fingerprint reference point detection for image retrieval based on symmetry and variation. Pattern Recognition, 45(9), 3360–3372.
- Lee, K., & Prabhakar, S. (2008). Probabilistic orientation field estimation for fingerprint enhancement and verification. In Proceedings on Biometric Symposium.
- Lee, B., Moon, J., & Kim, H. (2005). A novel measure of fingerprint image quality using the Fourier spectrum. In Proceedings of SPIE Conference on Biometric Technology for Human Identification II.
- Lee, C., Lee, S., Kim, J., & Kim, S. J. (2006). Preprocessing of a fingerprint image captured with a mobile camera. In Proceedings of International Conference on Biometrics (pp. 348–355).
- Lehtihet, R., El Oraiby, W., & Benmohammed, M. (2014). Ridge frequency estimation for low-quality fingerprint images enhancement using Delaunay triangulation. International Journal of Pattern Recognition and Artificial Intelligence, 28(1), 1456002.
- Leung, M., Engeler, W., & Frank, P. (1990). Fingerprint image processing using neural network. In Proceedings of IEEE Region 10 Conference on Computer and Communications Systems.
- Leung, W. F., Leung, S. H., Lau, W. H., & Luk, A. (1991). Fingerprint recognition using neural network. In Proceedings of Workshop Neural Network for Signal Processing.
- Li, J., Yau, W. Y., & Wang, H. (2006). Constrained nonlinear models of fingerprint orientations with prediction. Pattern Recognition, 39(1), 102–114.
- Li, G., Busch, C., & Yang, B. (2014). A novel approach used for measuring fingerprint orientation of arch fingerprint. In Proceedings of International Convention on Information and Communication Technology, Electronics and Microelectronics, Opatija (pp. 1309–1314).
- Li, J., Feng, J., & Kuo, C. C. J. (2018). Deep convolutional neural network for latent fingerprint enhancement. Signal Processing: Image Communication, 60, 52–63.
- Liang, X., & Asano, T. (2006). A linear time algorithm for binary fingerprint image denoising using distance transform. IEICE Transactions on Information and Systems, 89(4), 1534–1542.
- Lim, E., Jiang, X., & Yau, W. (2002). Fingerprint quality and validity analysis. In Proceedings of International Conference on Image Processing (Vol. 1, pp. 469–472).
- Lim, E., Toh, K. A., Suganthan, P. N., Jiang, X., & Yau, W. Y. (2004). Fingerprint image quality analysis. In Proceedings of International Conference on Image Processing (Vol. 2, pp. 1241–1244).
- Lin, W., & Dubes, R. (1983). A review of ridge counting in dermatoglyphics. Pattern Recognition, 16(1), 1–8.
- Liu, J., Huang, Z., & Chan, K. (2000). Direct minutiae extraction from gray-level fingerprint image by relationship examination. In Proceedings of International Conference on Image Processing.
- Liu, M., Jiang, X., & Kot, A. C. (2004). Fingerprint reference point detection. In Proceedings of International Conference on Biometric Authentication (pp. 272–279).
- Liu, T., Zhu, G., Zhang, C., & Hao, P. (2005). Fingerprint indexing based on singular point correlation. In Proceedings of International Conference on Image Processing (Vol. 2, pp. 293–296).
- Liu, T., Zhang, C., & Hao, P. (2006). Fingerprint reference point detection based on local axial symmetry. In Proceedings of 18th International Conference on Pattern Recognition (Vol. 1, pp. 1050–1053).
- Liu, S., & Liu, M. (2012). Fingerprint orientation modeling by sparse coding. In Proceedings of International Conference on Biometrics, New Delhi (pp. 176–181).
- Liu, M., Liu, S., & Zhao, Q. (2014). Fingerprint orientation field reconstruction by weighted discrete cosine transform. Information Sciences, 268, 65–77.
- Liu, E., & Cao, K. (2016). Minutiae extraction from level 1 features of fingerprint. IEEE Transactions on Information Forensics and Security, 11(9), 1893–1902.
- Liu, S., Liu, M., & Yang, Z. (2017). Sparse coding based orientation estimation for latent fingerprints. Pattern Recognition, 67, 164–176.
- Liu, J., Yan, J., Deng, D., & Zhang, R. (2020). Fingerprint image quality assessment based on BP neural network with hierarchical clustering. IET Information Security, 14(2), 185–195.
- Luo, X., & Tian, J. (2000). Knowledge based fingerprint image enhancement. In Proceedings of 15th International Conference on Pattern Recognition (Vol. 4, pp. 783–786).
- Ma, C., & Zhu, Y. (2013). Analysis and extraction of fingerprint features based on principal curves. Journal of Computational Information Systems, 9(21), 8591–8601.
- Maio, D., & Maltoni, D. (1996). A structural approach to fingerprint classification. In Proceedings of 13th International Conference on Pattern Recognition.
- Maio, D., & Maltoni, D. (1997). Direct gray-scale minutiae detection in fingerprints. IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(1).
- Maio, D., & Maltoni, D. (1998a). Ridge-line density estimation in digital images. In Proceedings of 14th International Conference on Pattern Recognition (pp. 1654–1658).
- Maio, D., & Maltoni, D. (1998b). Neural network based minutiae filtering in fingerprints. In Proceedings of 14th International Conference on Pattern Recognition (pp. 1654–1658).
- Maio, D., Maltoni, D., Cappelli, R., Wayman, J. L., & Jain, A. K. (2002). FVC2000: Fingerprint verification competition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(3), 402–412.
- Malathi, S., Uma Maheswari, S., & Meena, C. (2010). Fingerprint pore extraction based on marker controlled watershed segmentation. In Proceedings of International Conference on Computer and Automation Engineering, Singapore (pp. 337–340).
- Mallat, S. G. (1989). A theory for multiresolution signal decomposition: The wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(7), 674–693.
- Mehtre, B. M. (1993). Fingerprint image analysis for automatic identification. Machine Vision and Applications, 6, 124–139.
- Mehtre, B. M., Murthy, N. N., Kapoor, S., & Chatterjee, B. (1987). Segmentation of fingerprint images using the directional image. Pattern Recognition, 20(4), 429–435.
- Mei, Y., Sun, H., & Xia, D. (2009). A gradient-based combined method for the computation of fingerprints’ orientation field. Image and Vision Computing, 27(8), 1169–1177.
- Miao, D., Tang, Q., & Fu, W. (2007). Fingerprint minutiae extraction based on principal curves. Pattern Recognition Letters, 28(16), 2184–2189.
- Minaee, S., Boykov, Y., Porikli, F., Plaza, A., Kehtarnavaz, N., & Terzopoulos, D. (2021). Image segmentation using deep learning: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence. https://doi.org/10.1109/TPAMI.2021.3059968.
- Moayer, B., & Fu, K. (1986). A tree system approach for fingerprint pattern recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8(3), 376–388.
- Munir, M. U., Javed, M. Y., & Khan, S. A. (2012). A hierarchical k-means clustering based fingerprint quality classification. Neurocomputing, 85, 62–67.
- Nakamura, T., Hirooka, M., Fujiwara, H., & Sumi, K. (2004). Fingerprint image enhancement using a parallel ridge filter. In Proceedings of 17th International Conference on Pattern Recognition (Vol. 1, pp. 536–539).
- Nguyen, D., Cao, K., & Jain, A. K. (2018a). Automatic latent fingerprint segmentation. In Proceedings of International Conference on Biometrics: Theory, Applications and Systems.
- Nguyen, D., Cao, K., & Jain, A. K. (2018b). Robust minutiae extractor: Integrating deep networks and fingerprint domain knowledge. In Proceedings of International Conference on Biometrics.
- Nguyen, V. H., Liu, J., Nguyen, T. H. B., & Kim, H. (2020). Universal fingerprint minutiae extractor using convolutional neural networks. IET Biometrics, 9(2), 47–57.
- Nilsson, K., & Bigun, J. (2001). Using linear symmetry features as a pre-processing step for fingerprint images. In Proceedings of International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 247–252).
- Nilsson, K., & Bigun, J. (2002a). Complex filters applied to fingerprint images detecting prominent points used alignment. In Proceedings of ECCV Workshop on Biometric Authentication (pp. 39–47). Springer.
- Nilsson, K., & Bigun, J. (2002b). Prominent symmetry points as landmarks in fingerprint images for alignment. In Proceedings of 16th International Conference on Pattern Recognition (Vol. 3, pp. 395–398).
- Nilsson, K., & Bigun, J. (2003). Localization of corresponding points in fingerprints by complex filtering. Pattern Recognition Letters, 24(13), 2135–2144.
- NIST. (2015). Data Format for the Interchange of Fingerprint, Facial & Other Biometric Information. Update 2015 of NIST Special Publication 500-290e3.
- Novikov, S. O., & Kot, V. S. (1998). Singular feature detection and classification of fingerprints using hough transform. In Proceedings of SPIE (6th International Workshop on Digital Image Processing and Computer Graphics: Applications in Humanities and Natural Sciences) (Vol. 3346, pp. 259–269).
- O’Gorman, L., & Nickerson, J. (1988). Matched filter design for fingerprint image enhancement. In Proceedings of International Conference on Acoustic Speech and Signal Processing (pp. 916–919).
- O’Gorman, L., & Nickerson, J. V. (1989). An approach to fingerprint filter design. Pattern Recognition, 22(1), 29–38.
- Ohtsuka, T., & Kondo, A. (2005). A new approach to detect core and delta of the fingerprint using extended relational graph. In Proceedings of International Conference on Image Processing (Vol. 3, pp. 249–252).
- Ohtsuka, T., & Takahashi T. (2005). A new detection approach for the fingerprint core location using extended relation graph. IEICE Transactions on Information and Systems, 88(10), 2308–2312.
- Ohtsuka, T., & Watanabe, D. (2010). Singular candidate method: Improvement of extended relational graph method for reliable detection of fingerprint singularity. IEICE Transactions on Information and Systems, E93-D(7), 1788–1797.
- Oliveira, M. A., & Leite, N. J. (2008). A multiscale directional operator and morphological tools for reconnecting broken ridges in fingerprint images. Pattern Recognition, 41(1), 367–377.
- Orczyk, T., & Wieclaw, L. (2011). Fingerprint ridges frequency. In Proceedings World Congress on Nature and Biologically Inspired Computing, Salamanca (pp. 558–561).
- Ouyang, J., Feng, J., Lu, J., Guo, Z., & Zhou, J. (2017). Fingerprint pose estimation based on faster R-CNN. In Proceedings of International Joint Conference on Biometrics, Denver, CO (pp. 268–276).
- Pais Barreto Marques, A. C., & Gay Thome, A. C. (2005). A neural network fingerprint segmentation method. In Proceedings of International Conference on Hybrid Intelligent Systems.
- Paiva, A. R. C., & Tasdizen, T. (2012). Fingerprint image segmentation using data manifold characteristic features. International Journal of Pattern Recognition and Artificial Intelligence, 26(4), 1256010.
- Panetta, K., Kamath, K. M. S., Rajeev, S., & Agaian, S. S. (2019). LQM: localized quality measure for fingerprint image enhancement. IEEE Access, 7, 104567–104576.
- Perona, P. (1998). Orientation diffusions. IEEE Transactions on Image Processing, 7(3), 457–467.
- Prabhakar, S., Jain, A. K., & Pankanti, S. (2003). Learning fingerprint minutiae location and type. Pattern Recognition, 36(8), 1847–1857.
- Qi, J., Shi, Z., Zhao, X., & Wang, Y. (2005a). Measuring fingerprint image quality using gradient. In Proceedings of SPIE Conference on Biometric Technology for Human Identification II.
- Qi, J., Abdurrachim, D., Li, D., & Kunieda, H. (2005b). A hybrid method for fingerprint image quality calculation. In Proceedings of Workshop on Automatic Identification Advanced Technologies (pp. 124–129).
- Ram, S., Bischof, H., & Birchbauer, J. (2010). Modelling fingerprint ridge orientation using Legendre polynomials. Pattern Recognition, 43(1), 342–357.
- Rama, R. K. N. V., & Namboodiri, A. M. (2011). Fingerprint enhancement using hierarchical Markov random fields. In Proceedings of International Joint Conference on Biometrics, Washington, DC (pp. 1–8).
- Rämö, P., Tico, M., Onnia, V., & Saarinen, J. (2001). Optimized singular point detection algorithm for fingerprint images. In Proceedings of International Conference on Image Processing.
- Rao, A. R. (1990). A taxonomy for texture description and identification. Springer.
- Ratha, N. K., Chen, S. Y., & Jain, A. K. (1995). Adaptive flow orientation-based feature extraction in fingerprint images. Pattern Recognition, 28(11), 1657–1672.
- Ren, S., He, K., Girshick, R., & Sun, J. (2015). Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of Advances in Neural Information Processing Systems (pp. 91–99).
- Rerkrai, K., & Areekul, V. (2000). A new reference point for fingerprint recognition. In Proceedings of International Conference on Image Processing.
- Roddy, A., & Stosz, J. (1997). Fingerprint features: Statistical-analysis and system performance estimates. Proceedings of the IEEE, 85(9), 1390–1421.
- Ronneberger, O., Fischer, P., & Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. In Proceedings of International Conference on Medical Image Computing and Computer Assisted Intervention (pp. 234–241).
- Saleh, A. M., Bahaa Eldin, A. M., & Wahdan, A. A. (2009). A modified thinning algorithm for fingerprint identification systems. In Proceedings of International Conference on Computer Engineering & Systems, Cairo (pp. 371–376).
- Sankaran, A., Vatsa, M., & Singh, R. (2013). Automated clarity and quality assessment for latent fingerprints. In Proceedings of International Conference on Biometrics: Theory, Applications and Systems, Arlington, VA (pp. 1–6).
- Sankaran, A., Pandey, P., Vatsa, M., & Singh, R. (2014). On latent fingerprint minutiae extraction using stacked denoising sparse AutoEncoders. In Proceedings International Joint Conference on Biometrics, Clearwater, FL (pp. 1–7).
- Schuch, P., Schulz, S., & Busch, C. (2016). De-convolutional auto-encoder for enhancement of fingerprint samples. In Proceedings of International Conference on Image Processing Theory, Tools and Applications, Oulu (pp. 1–7).
- Schuch, P., Schulz, S., & Busch, C. (2017a). Deep expectation for estimation of fingerprint orientation fields. In Proceedings of International Joint Conference on Biometrics, Denver, CO (pp. 185–190).
- Schuch, P., Schulz, S., & Busch, C. (2017b). Intrinsic limitations of fingerprint orientation estimation. In Proceedings of International Conference of the Biometrics Special Interest Group, Darmstadt (pp. 1–5).
- Schuch, P., May, J. M., & Busch, C. (2018a). Unsupervised learning of fingerprint rotations. In Proceedings of International Conference of the Biometrics Special Interest Group, Darmstadt (pp. 1–6).
- Schuch, P., Schulz, S., & Busch, C. (2018b). Survey on the impact of fingerprint image enhancement. IET Biometrics, 7(2), 102–115.
- Sha, L., Zhao, F., & Tang, X. (2006). Minutiae-based fingerprint matching using subset combination. In Proceedings of International Conference on Pattern Recognition (Vol. 4, pp. 566–569).
- Sharma, R. P., & Dey, S. (2019). Two-stage quality adaptive fingerprint image enhancement using fuzzy C-means clustering based fingerprint quality analysis. Image and Vision Computing, 83–84, 1–16.
- Shen, L., Kot, A., & Koo, W. M. (2001). Quality measures of fingerprint images. In Proceedings of 3rd International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 266–271).
- Shen, Z., Xu, Y., Li, J., & Lu, G. (2019). Stable pore detection for high-resolution fingerprint based on a CNN detector. In Proceedings of International Conference on Image Processing, Taipei, Taiwan (pp. 2581–2585).
- Sherlock, B. G. (2004). Computer enhancement and modeling of fingerprint images. In N. Ratha & R. Bolle (Eds.), Automatic fingerprint recognition systems (pp. 87–112). Springer.
- Sherlock, B. G., & Monro, D. M. (1993). A model for interpreting fingerprint topology. Pattern Recognition, 26(7), 1047–1055.
- Sherlock, B. G., Monro, D. M., & Millard, K. (1992). Algorithm for enhancing fingerprint images. Electronics Letters, 28(18), 1720.
- Sherlock, B. G., Monro, D. M., & Millard, K. (1994). Fingerprint enhancement by directional Fourier filtering. IEE Proceedings Vision Image and Signal Processing, 141(2), 87–94.
- Shi, Z., & Govindaraju, V. (2006a). A chaincode based scheme for fingerprint feature extraction. Pattern Recognition Letters, 27(5), 462–468.
- Shi, Z., & Govindaraju, V. (2006b). Fingerprint image enhancement based on skin profile approximation. In Proceedings of 18th International Conference on Pattern Recognition (Vol. 3, pp. 714–717).
- Shi, Z., Wang, Y., Qi, J., & Xu, K. (2004). A new segmentation algorithm for low quality fingerprint image. In Proceedings of International Conference on Image and Graphics (pp. 314–317).
- Shin, J. H., Hwang, H. Y., & Chien, I. L. (2006). Detecting fingerprint minutiae by run length encoding scheme. Pattern Recognition, 39(6), 1140–1154.
- Singh, K., Gupta, A., & Kapoor, R. (2015). Fingerprint image super-resolution via ridge orientation-based clustered coupled sparse dictionaries. Journal of Electronic Imaging, 24(4), 043015.
- Srinivasan, V. S., & Murthy, N. N. (1992). Detection of singular points in fingerprint images. Pattern Recognition, 25(2), 139–153.
- Stock, R. M., & Swonger, C. W. (1969). Development and Evaluation of a Reader of Fingerprint Minutiae. Technical Report: XM–2478–X–1:13–17, Cornell Aeronautical Laboratory.
- Stoney, D. A., & Thornton, J. I. (1987). A systematic study of epidermal ridge minutiae. Journal of Forensic Sciences, 32(5), 1182–1203.
- Stosz, J. D., & Alyea, L. A. (1994). Automated system for fingerprint authentication using pores and ridge structure. In Proceedings of SPIE (Automatic Systems for the Identification and Inspection of Humans) (Vol. 2277, pp. 210–223).
- Su, Y., Feng, J., & Zhou, J. (2016). Fingerprint indexing with pose constraint. Pattern Recognition, 54, 1–13.
- Sudiro, S. A., Paindavoine, M., & Kusuma, T. M. (2007). Simple fingerprint minutiae extraction algorithm using crossing number on valley structure. In Proceedings of Workshop on Automatic Identification Advanced Technologies (pp. 41–44).
- Sutthiwichaiporn, P., & Areekul, V. (2013). Adaptive boosted spectral filtering for progressive fingerprint enhancement. Pattern Recognition, 46(9), 2465–2486.
- Svoboda, J., Monti, F., & Bronstein, M. M. (2017). Generative convolutional networks for latent fingerprint reconstruction. In Proceedings of International Joint Conference on Biometrics (pp. 429–436).
- Székely, E., & Székely, V. (1993). Image recognition problems of fingerprint identification. Microprocessors and Microsystems, 17(4), 215–218.
- Tabassi, E., Wilson, C., & Watson, C. (2004). Fingerprint Image Quality. NIST Research Report: NISTIR 7151.
- Tabassi, E., Olsen, M. A., Makarov, A., & Busch, C. (2013). Towards NFIQ II lite—Self-organizing Maps for Fingerprint Image Quality assessment. NIST Interagency Report 79.
- Tabassi, E., Olsen, M., Bausinger, O., Busch, C., Figlarz, A., Fiumara, G., Henniger, O., Merkle, J., Ruhland, T., Schiel, C., & Schwaiger, M. (2021). NFIQ 2.0—NIST Fingerprint Image Quality. NIST-IR 8382. https://doi.org/10.6028/NIST.IR.8382. Accessed July 2021.
- Tamura, H. (1978). A comparison of line thinning algorithms from digital topology viewpoint. In Proceedings of 4th International Conference on Pattern Recognition (pp. 715–719).
- Tang, Y., Gao, F., & Feng, J. (2017a). Latent fingerprint minutia extraction using fully convolutional network. In Proceedings of International Joint Conference on Biometrics, Denver, CO (pp. 117–123).
- Tang, Y., Gao, F., Feng, J., & Liu, Y. (2017b). FingerNet: An unified deep network for fingerprint minutiae extraction. In Proceedings of International Joint Conference on Biometrics, Denver, CO (pp. 108–116).
- Tao, X., Yang, X., Cao, K., Wang, R., Li, P., & Tian, J. (2010). Estimation of fingerprint orientation field by weighted 2D Fourier expansion model. In Proceedings of International Conference on Pattern Recognition, Istanbul (pp. 1253–1256).
- Tao, X., Yang, X., Zang, Y., Jia, X., & Tian, J. (2012). A novel measure of fingerprint image quality using Principal Component Analysis (PCA). In Proceedings of International Conference on Biometrics, New Delhi (pp. 170–175).
- Tashk, A., Helfroush, M. S., & Muhammadpour, M. (2009). Improvement of fingerprint orientation estimation by a modification of fingerprint orientation model based on 2D Fourier expansion (M-FOMFE). In Proceedings International Conference on Computer, Control and Communication, Karachi (pp. 1–6).
- Teixeira, R. F. S., & Leite, N. J. (2013). On adaptive fingerprint pore extraction. In Proceedings of International Conference on Image Analysis and Recognition (pp. 72–79).
- Teixeira, R. F. S., & Leite, N. J. (2014). Improving pore extraction in high resolution fingerprint images using spatial analysis. In Proceedings of International Conference on Image Processing, Paris (pp. 4962–4966).
- Teixeira, R. F. S., & Leite, N. J. (2017). A new framework for quality assessment of high-resolution fingerprint images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39(10), 1905–1917.
- Thai, D. H., & Gottschlich, C. (2016). Global variational method for fingerprint segmentation by three-part decomposition. IET Biometrics, 5(2), 120–130.
- Trier, O., & Jain, A. K. (1995). Goal-directed evaluation of binarization methods. IEEE Transactions on Pattern Analysis and Machine Intelligence, 17(12), 1191–1201.
- Turroni, F., Maltoni, D., Cappelli, R., & Maio, D. (2011). Improving fingerprint orientation extraction. IEEE Transactions on Information Forensics and Security, 6(3), 1002–1013.
- Uchida, K. (2004). Image-based approach to fingerprint acceptability assessment. In Proceedings of International Conference on Biometric Authentication (pp. 294–300).
- Van, T. H., & Le, H. T. (2009a). An efficient algorithm for fingerprint reference-point detection. In Proceedings of International Conference on Computing and Communication Technologies, Da Nang (pp. 1–7).
- Van, T. H., & Le, H. T. (2009b). Adaptive noisy fingerprint enhancement based on orientation consistency. In Proceedings of International Conference on Knowledge and Systems Engineering, Hanoi (pp. 67–72).
- Verma, M. R., Majumdar, A. K., & Chatterjee, B. (1987). Edge detection in fingerprints. Pattern Recognition, 20, 513–523.
- Vernon, D. S. G. (1993). Automatic detection of secondary creases in fingerprints. Optical Engineering, 32(10), 2616–2623.
- Viola, P., & Jones, M. J. (2001). Rapid object detection using a boosted cascade of simple features. In Proceedings of International Conference on Computer Vision and Pattern Recognition (pp. 511–518).
- Vizcaya, P. R., & Gerhardt, L. A. (1996). A nonlinear orientation model for global description of fingerprints. Pattern Recognition, 29(7), 1221–1231.
- Wahab, A., Chin, S. H., & Tan, E. C. (1998). Novel approach to automated fingerprint recognition. IEE Proceedings Vision Image and Signal Processing, 145(3), 160–166.
- Wahab, A., Tan, E. C., & Jonatan, A. (2004). Direct gray-scale minutiae extraction. In Proceedings of International Conference on Biometric Authentication (pp. 280–286).
- Wang, Y., & Hu, J. (2008). estimate singular point rotation by analytical models. In Proceedings of SPIE Conference on Biometric Technology for Human Identification V.
- Wang, Y., & Hu, J. (2011). Global ridge orientation modeling for partial fingerprint identification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 33(1), 72–87.
- Wang, L., Suo, H., & Dai, M. (2005). Fingerprint image segmentation based on Gaussian–Hermite moments. In Proceedings of International Conference on Advanced Data Mining and Applications.
- Wang, Y., Hu, J., & Phillips, D. (2007a). A fingerprint orientation model based on 2D Fourier expansion (FOMFE) and its application to singular-point detection and fingerprint indexing. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(4), 573–585.
- Wang, X., Li, J., & Niu, Y. (2007b). Definition and extraction of stable points from fingerprint images. Pattern Recognition, 40(6), 1804–1815.
- Wang, W., Li, J., Huang, F., & Feng, H. (2008). Design and implementation of Log-Gabor filter in fingerprint image enhancement. Pattern Recognition Letters, 29(3), 301–308.
- Wang, J., Li, J., & Cao, L. (2011). An improved fast thinning algorithm for fingerprint image and its application. Journal of Computational Information Systems, 7(7), 2285–2292.
- Watson, C. I. (1993). NIST special database 14, fingerprint database. U.S. National Institute of Standards and Technology.
- Watson, C. I., & Wilson, C. L. (1992). NIST special database 4, fingerprint database. U.S. National Institute of Standards and Technology.
- Watson, C. I., Candela, G. I., & Grother, P. J. (1994). Comparison of FFT fingerprint filtering methods for neural network classification. Technical Report: NIST TR 5493, September 1994.
- Weber, D. M. (1992). A cost effective fingerprint verification algorithm for commercial applications. In Proceedings of South African Symposium on Communication and Signal Processing.
- Wegstein, J. H. (1982). An automated fingerprint identification system. U.S. Government Publication, U.S. Department of Commerce, National Bureau of Standards, Washington, DC.
- Weng, D., Yin, Y., & Yang, D. (2011). Singular points detection based on multi-resolution in fingerprint images. Neurocomputing, 74(17), 3376–3388.
- Willis, A. J., & Myers, L. (2001). A cost-effective fingerprint recognition system for use with low-quality prints and damaged fingertips. Pattern Recognition, 34(2), 255–270.
- Wong, W. J., & Lai, S. H. (2020). Multi-task CNN for restoring corrupted fingerprint images. Pattern Recognition, 101, 107203.
- Wu, J. C., & Garris, M. D. (2007). Nonparametric statistical data analysis of fingerprint minutiae exchange with two-finger fusion. In Proceedings of SPIE Conference on Biometric Technology for Human Identification IV.
- Wu, C., & Govindaraju, V. (2006). Singularity preserving fingerprint image adaptive filtering. In Proceedings of International Conference on Image Processing (pp. 313–316).
- Wu, N., & Zhou, J. (2004). Model based algorithm for singular point detection from fingerprint images. In Proceedings of International Conference on Image Processing (Vol. 2, pp. 885–888).
- Wu, C., Zhou, J., Bian, Z., & Rong, G. (2003). Robust crease detection in fingerprint images. In Proceedings of Conference on Computer Vision and Pattern Recognition (Vol. II, pp. 505–510).
- Xiang, M., Wu, X., & Hua, Q. (2009). A fast thinning algorithm for fingerprint image. In Proceedings of International Conference on Information Science and Engineering, Nanjing (pp. 1039–1042).
- Xiao, Q., & Raafat, H. (1991). Fingerprint image post-processing: A combined statistical and structural approach. Pattern Recognition, 24(10), 985–992.
- Yang, J., Liu, L., Jiang, T., & Fan, Y. (2003). A modified Gabor filter design method for fingerprint image enhancement. Pattern Recognition Letters, 24(12), 1805–1817.
- Yang, J., Xiong, N., & Vasilakos, A. V. (2013). Two-stage enhancement scheme for low-quality fingerprint images by learning from the images. IEEE Transactions on Human-Machine Systems, 43(2), 235–248.
- Yang, X., Feng, J., & Zhou, J. (2014). Localized dictionaries based orientation field estimation for latent fingerprints. IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(5), 955–969.
- Yao, M. Y. S., Pankanti, S., & Hass, N. (2004). Fingerprint quality assessment. In N. Ratha & R. Bolle (Eds.), Automatic fingerprint recognition systems (pp. 55–66). Springer.
- Yao, Z., Le bars, J., Charrier, C., & Rosenberger, C. (2015). Quality assessment of fingerprints with minutiae delaunay triangulation. In Proceedings of International Conference Information Systems Security and Privacy (pp. 315–321).
- Yao, Z., Le Bars, J., Charrier, C., & Rosenberger, C. (2018). Comparative study of digital fingerprint quality assessment metrics. In Proceedings of International Conference on Biometrics, Gold Coast, QLD (pp. 17–22).
- Yin, Y., Wang, Y., & Yang, X. (2005). Fingerprint image segmentation based on quadric surface model. In Proceedings of 5th International Conference on Audio- and Video-Based Biometric Person Authentication (pp. 647–655).
- Yoon, S., Cao, K., Liu, E., & Jain, A. K. (2013). LFIQ: latent fingerprint image quality. In Proceedings of International Conference on Biometrics: Theory, Applications and Systems, Washington, D.C.
- Young, M. R., & Elliott, S. J. (2007). Image quality and performance based on henry classification and finger location. In Proceedings of Workshop on Automatic Identification Advanced Technologies (pp. 51–56).
- Zacharias, G. C., Nair, M. S., & Lal, P. S. (2017). Fingerprint reference point identification based on chain encoded discrete curvature and bending energy. Pattern Analysis and Applications, 20(1), 253–267.
- Zhan, X., Sun, Z., Yin, Y., & Chu, Y. (2006). Fingerprint ridge distance estimation: Algorithms and the performance. In Proceedings of International Conference on Biometrics (pp. 294–301).
- Zhang, Q., & Yan, H. (2007). Fingerprint orientation field interpolation based on the constrained Delaunay triangulation. International Journal of Information and Systems Sciences, 3(3), 438–452.
- Zhang, D., Liu, F., Zhao, Q., Lu, G., & Luo, N. (2011a). Selecting a reference high resolution for fingerprint recognition using minutiae and pores. IEEE Transactions on Instrumentation and Measurement, 60(3), 863–871.
- Zhang, H., Miao, D., & Zhong, C. (2011b). Modified principal curves based fingerprint minutiae extraction and pseudo minutiae detection. International Journal of Pattern Recognition and Artificial Intelligence, 25(8), 1243–1260.
- Zhang, J., Lai, R., & Kuo, C. J. (2012a). Latent fingerprint segmentation with adaptive total variation model. In Proceedings of International Conference on Biometrics, New Delhi (pp. 189–195).
- Zhang, J., Lai, R., & Kuo, C. J. (2012b). Latent fingerprint detection and segmentation with a directional total variation model. In Proceedings of International Conference on Image Processing (pp. 1145–1148).
- Zhang, J., Lai, R., & Kuo, C. J. (2013). Adaptive directional total-variation model for latent fingerprint segmentation. IEEE Transactions on Information Forensics and Security, 8(8), 1261–1273.
- Zhang, N., Zang, Y., Yang, X., Jia, X., & Tian, J. (2014). Adaptive orientation model fitting for latent overlapped fingerprints separation. IEEE Transactions on Information Forensics and Security, 9(10), 1547–1556.
- Zhao, Q., & Jain, A. K. (2010). On the utility of extended fingerprint features: A study on pores. In Proceedings of CVPR Workshop on Biometrics, San Francisco.
- Zhao, Q., & Jain, A. K. (2012). Model based separation of overlapping latent fingerprints. IEEE Transactions on Information Forensics and Security, 7(3), 904–918.
- Zhao, F., & Tang, X. (2007). Preprocessing and postprocessing for skeleton-based fingerprint minutiae extraction. Pattern Recognition, 40(4), 1270–1281.
- Zhao, Q., Zhang, L., Zhang, D., Huang, W., & Bai, J. (2009). Curvature and singularity driven diffusion for oriented pattern enhancement with singular points. In Proceedings of Conference on Computer Vision and Pattern Recognition, Miami, FL (pp. 2129–2135).
- Zhao, Q., Zhang, D., Zhang, L., & Luo, N. (2010a). High resolution partial fingerprint alignment using pore-valley descriptors. Pattern Recognition, 43(3), 1050–1061.
- Zhao, Q., Zhang, D., Zhang, L., & Luo, N. (2010b). Adaptive fingerprint pore modeling and extraction. Pattern Recognition, 43(8), 2833–2844.
- Zhao, Q., Liu, F., Zhang, L., & Zhang, D. (2010c). A comparative study on quality assessment of high resolution fingerprint images. In Proceedings of International Conference on Image Processing, Hong Kong (pp. 3089–3092).
- Zhou, J., & Gu, J. (2004a). A model-based method for the computation of fingerprints’ orientation field. IEEE Transactions on Image Processing, 13(6), 821–835.
- Zhou, J., & Gu, J. (2004b). Modeling orientation fields of fingerprints with rational complex functions. Pattern Recognition, 37(2), 389–391.
- Zhou, J., Wu, C., Bian, Z., & Zhang, D. (2004). Improving fingerprint recognition based on crease detection. In Proceedings of International Conference on Biometric Authentication (pp. 287–293).
- Zhou, J., Gu, J., & Zhang, D. (2007). Singular points analysis in fingerprints based on topological structure and orientation field. In Proceedings of International Conference on Biometrics (pp. 261–270).
- Zhou, J., Chen, F., Gu, J. (2009a). A novel algorithm for detecting singular points from fingerprint images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(7), 1239–1250.
- Zhou, J., Chen, F., Wu, N., & Wu, C. (2009b). Crease detection from fingerprint images and its applications in elderly people. Pattern Recognition, 42(5), 896–906.
- Zhu, E., Yin, J., & Zhang, G. (2004). Fingerprint enhancement using circular Gabor filter. In Proceedings of International Conference on Image on Analysis and Recognition (pp. 750–758).
- Zhu, E., Yin, J., Hu, C., & Zhang, G. (2005). Quality estimation of fingerprint image based on neural network. In Proceedings of International Conference on Natural Computation (pp. 65–70).
- Zhu, E., Yin, J., Hu, C., & Zhang, G. (2006). A systematic method for fingerprint ridge orientation estimation and image segmentation. Pattern Recognition, 39(8), 1452–1472.
- Zhu, E., Guo, X., & Yin, J. (2016). Walking to singular points of fingerprints. Pattern Recognition, 56, 116–128.
- Zhu, Y., Yin, X., Jia, X., & Hu, J. (2017). Latent fingerprint segmentation based on convolutional neural networks. In Proceedings of Workshop on Information Forensics and Security, Rennes (pp. 1–6).
版权归原作者 minutiae 所有, 如有侵权,请联系我们删除。