我幼儿园的弟看了都直呼简单的【栈和队列】

目录

1. 栈

1.1 栈的概念及结构

栈：一种特殊的线性表(在逻辑上是连续存储的，物理上不一定连续)，其只允许在固定的一端进行插入和删除元素操作。
进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。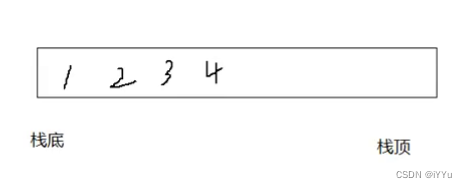

例如上面在栈中的数据只能先依次拿出栈顶的数据，出栈的顺序依此是4，3，2，1，入栈时是1，2，3，4，所以后进先出也可以理解为先进后出。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈，出数据也在栈顶。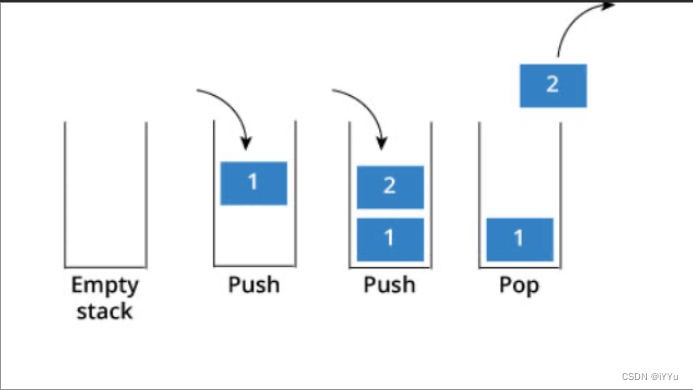

注意：这里的栈是数据结构里的栈，主要是在内存堆区中对数据进行管理。而不是操作系统中划分内存区域中的栈，但是都有一个特点，都遵循后进先出。

1.2 实现栈

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小，并且数组的地址是连续的，访问起来缓存的利用率也会更高一些。

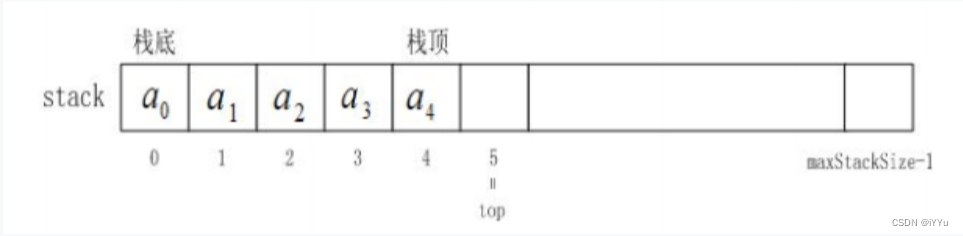
但因为数组并不是随时动态开辟的空间，如果数组元素满了需要考虑扩容，一次扩容原来的2倍，势必会有一些空间上的浪费。
如果比较在意空间，可以使用带头双向链表，这是比较方便的，如果使用单链表，要把链表的头结点作为栈顶，尾结点作为栈底，因为链表的头插头删比较高效。

代码实现：

//函数声明#pragmaonce#include<stdio.h>#include<assert.h>#include<stdlib.h>#include<stdbool.h>//创建栈typedefint DATATYPE;typedefstructStack{
    DATATYPE* stack;int top;int capacity;}Stack;//初始化栈voidInintStack(Stack* ptrs);//入栈voidPushStack(Stack* ptrs, DATATYPE data);//出栈voidPopStack(Stack* ptrs);//访问栈顶数据
DATATYPE StackTop(Stack* ptrs);//判断栈是否为空
bool StackEmpty(Stack* ptrs);//数据个数intStackSize(Stack* ptrs);//销毁栈voidDestroyStack(Stack* ptrs);

注意：不要直接访问结构体中的数据，即使非常简单也要封装为一个函数来访问。

//函数实现#define_CRT_SECURE_NO_WARNINGS1#include"StackQueue.h"//初始化栈voidInintStack(Stack* ptrs){assert(ptrs);
    ptrs->stack =NULL;//注意如果初始话top为0//那么栈顶的元素下标时top-1
    ptrs->top = ptrs->capacity =0;}//检查容量voidcheckSys(Stack* ptrs){if(ptrs->capacity == ptrs->top){int newCapacity = ptrs->capacity ==0?sizeof(DATATYPE):2* ptrs->capacity;
        DATATYPE* ret =(DATATYPE*)realloc(ptrs->stack,sizeof(DATATYPE)* newCapacity);if(!ret){perror("calloc fali");exit(-1);}
        ptrs->stack = ret;
        ptrs->capacity = newCapacity;}}//入栈voidPushStack(Stack* ptrs, DATATYPE data){assert(ptrs);checkSys(ptrs);
    ptrs->stack[ptrs->top++]= data;}//出栈voidPopStack(Stack* ptrs){assert(ptrs);assert(!StackEmpty(ptrs));
    ptrs->top--;}//访问栈顶数据
DATATYPE StackTop(Stack* ptrs){assert(ptrs);assert(!StackEmpty(ptrs));return ptrs->stack[ptrs->top -1];}//判断栈是否为空
bool StackEmpty(Stack* ptrs){assert(ptrs);return ptrs->top ==0;}//数据个数intStackSize(Stack* ptrs){assert(ptrs);return ptrs->top;}//销毁栈voidDestroyStack(Stack* ptrs){assert(ptrs);free(ptrs->stack);
    ptrs->top = ptrs->capacity =0;
    ptrs->stack =NULL;}

//测试逻辑#define_CRT_SECURE_NO_WARNINGS1#include"StackQueue.h"voidtest(){
    Stack sk;InintStack(&sk);PushStack(&sk,1);PushStack(&sk,2);printf("%d ",StackTop(&sk));PopStack(&sk);PushStack(&sk,3);PushStack(&sk,4);printf("%d ",StackTop(&sk));PopStack(&sk);PushStack(&sk,5);PushStack(&sk,6);//遍历完栈就相当于清空栈了while(!StackEmpty(&sk)){printf("%d ",StackTop(&sk));PopStack(&sk);}DestroyStack(&sk);}intmain(){test();return0;}

2. 队列

2.1 队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)的规则。
入队列：进行插入操作的一端称为队尾
出队列：进行删除操作的一端称为队头。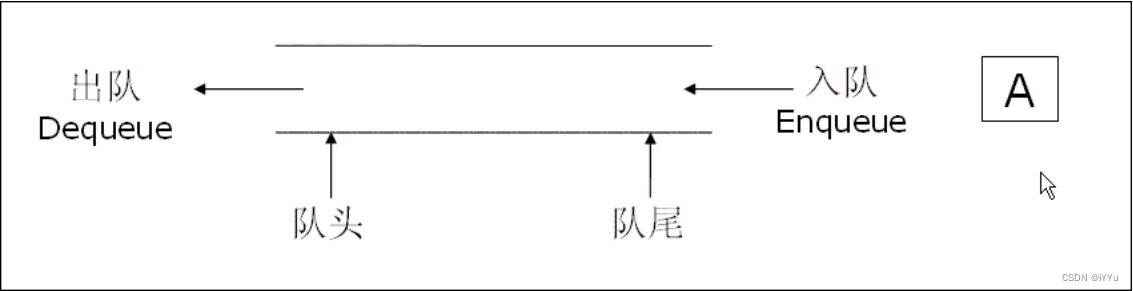

2.2 队列的实现

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，就需要挪动后面的数据，效率会比较低。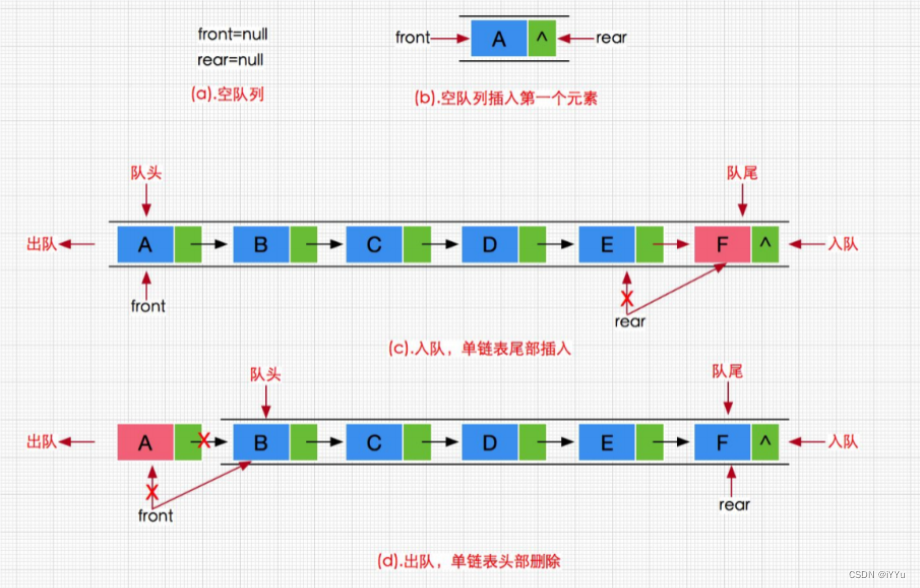

代码实现：

//函数声明#pragmaonce#include<stdio.h>#include<assert.h>#include<stdlib.h>#include<stdbool.h>//创建队列typedefint QDataType;typedefstructQueueNode{
    QDataType data;structQueueNode* next;}QNode;//因为队列只有头删尾插//因此需要定义两个指针//一个指向队头，另一个指向队尾typedefstructQueue{
    QNode* head;
    QNode* tail;int size;}Queue;// 初始化队列voidQueueInit(Queue* q);// 队尾入队列voidQueuePush(Queue* q, QDataType data);// 队头出队列voidQueuePop(Queue* q);// 获取队列头部元素
QDataType QueueFront(Queue* q);// 获取队列队尾元素
QDataType QueueBack(Queue* q);// 获取队列中有效元素个数intQueueSize(Queue* q);// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 intQueueEmpty(Queue* q);// 销毁队列voidQueueDestroy(Queue* q);

//函数实现#define_CRT_SECURE_NO_WARNINGS1#include"Queue.h"// 初始化队列voidQueueInit(Queue* q){assert(q);
    q->head = q->tail =NULL;
    q->size =0;}// 队尾入队列voidQueuePush(Queue* q, QDataType data){assert(q);
    QNode* newnode =(QNode*)malloc(sizeof(QNode));if(!newnode){perror("malloc fail");exit(-1);}
    newnode->data = data;
    newnode->next =NULL;//当头指针为空需要特殊处理if(q->head ==NULL){
        q->head = q->tail = newnode;}else{
        q->tail->next = newnode;
        q->tail = q->tail->next;}
    q->size++;}// 队头出队列voidQueuePop(Queue* q){assert(q);assert(!QueueEmpty(q));if(q->head->next ==NULL){free(q->head);
        q->head = q->tail =NULL;
        q->size =0;}else{
        QNode* del = q->head;
        q->head = q->head->next;free(del);
        del =NULL;

        q->size--;}}// 获取队列头部元素
QDataType QueueFront(Queue* q){assert(q);assert(!QueueEmpty(q));return q->head->data;}// 获取队列队尾元素
QDataType QueueBack(Queue* q){assert(q);assert(!QueueEmpty(q));return q->tail->data;}// 获取队列中有效元素个数intQueueSize(Queue* q){assert(q);return q->size;}// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 intQueueEmpty(Queue* q){assert(q);return q->head ==NULL&& q->tail ==NULL;}// 销毁队列voidQueueDestroy(Queue* q){assert(q);
    QNode* cur = q->head;while(cur){
        QNode* del = cur;
        cur = cur->next;free(del);
        del =NULL;}
    q->head = q->tail =NULL;}

//主逻辑测试voidtestQueue(){
    Queue qq;QueueInit(&qq);QueuePush(&qq,1);QueuePush(&qq,2);printf("%d ",QueueFront(&qq));QueuePop(&qq);QueuePush(&qq,3);QueuePush(&qq,4);printf("%d ",QueueFront(&qq));QueuePop(&qq);QueuePush(&qq,5);while(!QueueEmpty(&qq)){printf("%d ",QueueFront(&qq));QueuePop(&qq);}QueueDestroy(&qq);}intmain(){//testStack();testQueue();return0;}

注意：一个入队列顺序对应一个出队列顺序，一个入栈顺序对应多个出栈顺序

3. 概念选择题

1. 一个栈的初始 状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（ ）。 A 12345ABCDE B EDCBA54321 C ABCDE12345 D 54321EDCBA
2. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（） A 1,4,3,2 B 2,3,4,1 C 3,1,4,2 D 3,4,2,1
3. 现有一循环队列，其队头指针为front，队尾指针为rear；循环队列长度为N。其队内有效长度为？(假设多给一个空间，实际长度为N) A (rear - front + N) % N + 1 B (rear - front + N) % N C (rear - front) % (N + 1) D (rear - front + N) % (N - 1)

答案：1.B 2.C 3.B

第一题很简单，先进后出原则。
第二题需要注意的是在入栈的过程中是可以直接出栈的，比如说入栈的顺序为1，2，3，4，那么出栈的顺序也是1，2，3，4这是因为可以入1出1，入2出2…，因此只需要往选项中代入就可以找出不可能的一个顺序。
一个入栈顺序是可能有多个出栈顺序。
第三题实际长度为N，有效范围为N-1，直接带入即可求出当前的有效数据。

4. 栈和队列OJ题

4.1 括号匹配问题

来源：Leetcode。OJ链接

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

解题思路：本题解法所需要的数据结构正是栈。

1. 当遍历到左括号时入栈
2. 遍历到右括号时，拿出栈顶的元素进行比较，如果对应的左括号不匹配返回0

//直接造轮子！//创建栈//...//把上面实现的栈原封不动的拷贝下来
bool isValid(char* s){
    Stack sk;InintStack(&sk);for(int i=0; s[i];++i){if(s[i]=='('|| s[i]=='['|| s[i]=='{'){//左括号入栈PushStack(&sk, s[i]);}else{if(StackEmpty(&sk)){//如果第一个就是右括号，栈为空，说明不匹配DestroyStack(&sk);return0;}
            DATATYPE ret =StackTop(&sk);if(s[i]==')'&& ret !='('|| s[i]==']'&& ret !='['|| s[i]=='}'&& ret !='{'){DestroyStack(&sk);return0;}//没次弹出栈顶元素PopStack(&sk);}}//最后判断栈里的元素是否为空//为空才为正确答案int flag =StackEmpty(&sk);DestroyStack(&sk);return flag;}

4.2 用队列实现栈

来源：Leetcode。OJ链接

题目描述：请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

思路：由于队列的性质是先进先出，和栈先进后出相反，因此需要用到两个队列q1和q2，其中一个为push的队列，另一个为pop的辅助队列。
具体地，当pop时，找到两个中不为空的队列，把不为空的前N-1个数据全部依次push到为空的辅助队列，此时剩下的一个元素(队尾的元素)即为栈顶元素，pop后此队列为空。当下一次pop时，也是同样的操作。

//造轮子//...//...//把上面实现的队列原封不动的拷贝下来//创建两个队列typedefstruct{
    Queue q1;
    Queue q2;} MyStack;//初始化
MyStack*myStackCreate(){
    MyStack* obj =(MyStack*)malloc(sizeof(MyStack));QueueInit(&obj->q1);QueueInit(&obj->q2);return obj;}//push元素到空队列voidmyStackPush(MyStack* obj,int x){if(!QueueEmpty(&obj->q1)){QueuePush(&obj->q1, x);}else{QueuePush(&obj->q2, x);}}//找到不为空的一个队列//把前N-1个数据全部push到空队列中//返回最后一个元素后popintmyStackPop(MyStack* obj){
    Queue* empty =&obj->q1,*noempty =&obj->q2;if(!QueueEmpty(empty)){
        empty =&obj->q2;
        noempty =&obj->q1;}//非空队列的N-1个元素导入到空队列，剩下的一个就是栈顶元素while(QueueSize(noempty)>1){QueuePush(empty,QueueFront(noempty));QueuePop(noempty);}int tmp =QueueFront(noempty);QueuePop(noempty);return tmp;}//返回不为空队列的队尾的元素，即栈顶元素intmyStackTop(MyStack* obj){if(!QueueEmpty(&obj->q1)){returnQueueBack(&obj->q1);}else{returnQueueBack(&obj->q2);}}//两个队列都为空才是空
bool myStackEmpty(MyStack* obj){returnQueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);}//释放队列voidmyStackFree(MyStack* obj){QueueDestroy(&obj->q1);QueueDestroy(&obj->q2);free(obj);}

4.3 用栈实现队列

来源：Leetcode。OJ链接
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

解题思路：栈的规则是先进后出，如何利用两个栈实现先进先出模拟队列？
不难发现，如果一个栈只入数据，另一个栈从入栈中依次取出栈顶的数据后再出栈，这种出栈的顺序正好符合先进先出。
具体地，定义一个入栈s1，出栈s2，当入数据全部入到s1中，当出数据时判断s2是否为空，如果为空，开始从s1的栈顶取出数据，每次取出后，pop掉s1中栈顶的数据。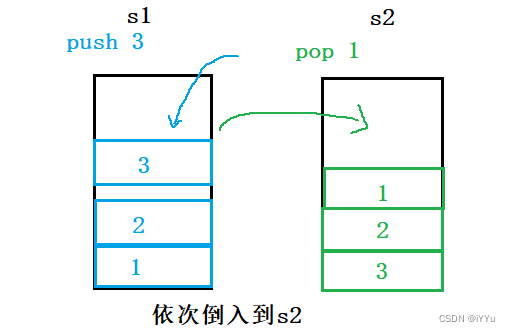
全部取出放入s2后，再进行出栈操作，数据的出栈顺序就变成了先进先出。
s2的栈顶就可以理解为队列的队头，此时s2栈顶的数据依次出栈(出队)，就模拟出了队列的效果。

//造轮子//...//...//把上面实现的栈原封不动的拷贝下来//创建结构体typedefstruct{
    Stack s1;
    Stack s2;} MyQueue;//创建两个栈//s1是入栈//s2是出栈
MyQueue*myQueueCreate(){
    MyQueue* obj =(MyQueue*)malloc(sizeof(MyQueue));InintStack(&obj->s1);InintStack(&obj->s2);return obj;}//入栈的数据直接存放到s1中voidmyQueuePush(MyQueue* obj,int x){PushStack(&obj->s1, x);}//判断入栈是否为空//如果为空则把入栈的数据全部取出放入出栈中//这样才符合队列的先进先出voidPushToPop(Stack* push, Stack* pop){if(StackEmpty(pop)){while(!StackEmpty(push)){PushStack(pop,StackTop(push));PopStack(push);}}}//出队并删除队头元素//(栈的规则是先进后出，把入栈的顺序反过来就变成了先进先出，也就是队列的规则)intmyQueuePop(MyQueue* obj){PushToPop(&obj->s1,&obj->s2);int top =StackTop(&obj->s2);PopStack(&obj->s2);return top;}//出队intmyQueuePeek(MyQueue* obj){PushToPop(&obj->s1,&obj->s2);returnStackTop(&obj->s2);}//两个栈都不为空
bool myQueueEmpty(MyQueue* obj){returnStackSize(&obj->s1)==0&&StackSize(&obj->s2)==0;}//释放栈voidmyQueueFree(MyQueue* obj){free((&obj->s1)->stack);free((&obj->s2)->stack);free(obj);}

4.4 设计循环队列

来源：Leetcode。OJ链接

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k 。
• Front: 从队首获取元素。如果队列为空，返回 -1 。
• Rear: 获取队尾元素。如果队列为空，返回 -1 。
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
• isEmpty(): 检查循环队列是否为空。
• isFull(): 检查循环队列是否已满。

环形队列可以使用数组实现，也可以使用循环链表实现。

环形队列第一个比较棘手的问题是如何判空以及如何判满，有两种方法：
1、添加一个size变量用来记录数据个数
2、额外增加一个空间，满的时候永远留一个位置。比如说有效数据个数为4，那么开空间时开辟5个数据的空间，在判断时会比较方便。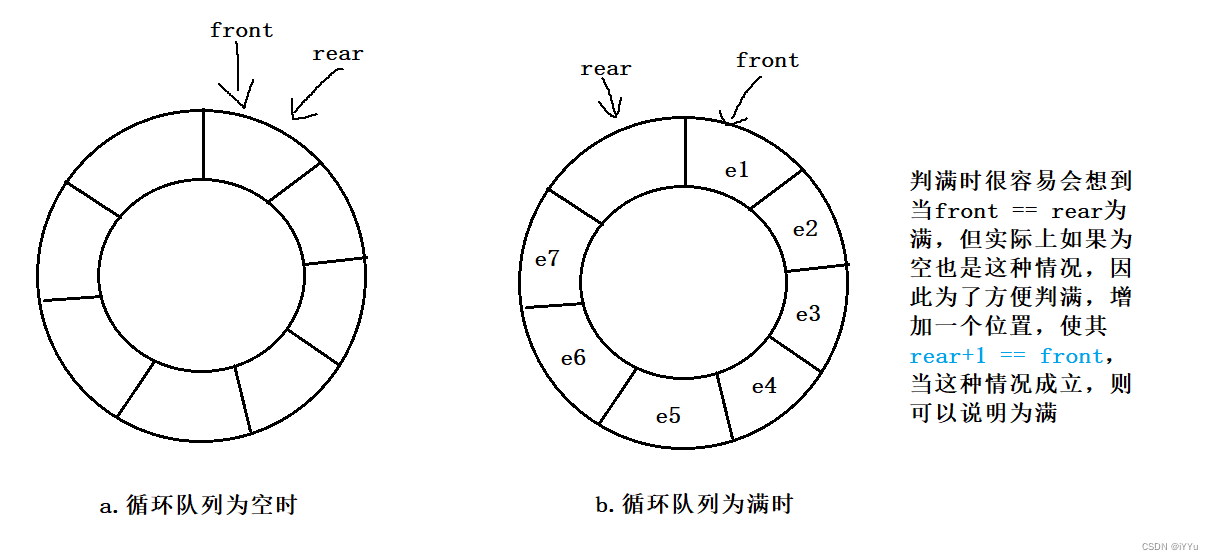

如上图，到这里其实可以发现使用链表来实现的话会有一个不好的地方，不方便取出尾结点的数据，因为rear那地方并不是有效数据的位置，除非再定义一个指针，指向尾结点的前一个结点，但是实现起来就比较麻烦了。但是使用数组就比较方便访问了，因为可以支持下标快速访问，无需遍历，rear-1就可以取出最后一个位置的数据，因此这题选择数组来实现。

如果选择数组，还有一个小问题是判满情况，判满的表达式为rear+1 == front，如果下标rear+1越界了如何处理？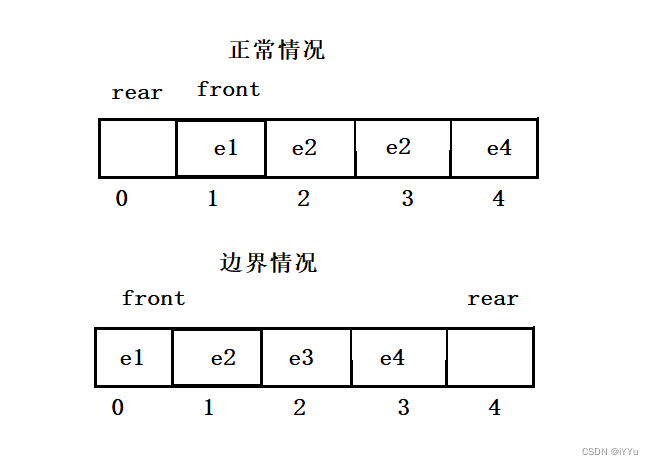

可以使用取模运算来巧妙地解决这个问题，因为该数组的实际大小为5(下标访问范围为04)，而实际有效的范围为4(下标访问范围为03)，因此，当rear的下标为4的时候，说明到了数组的最后一个位置，此时令(rear+1) %= 5，让其回到数组最开头的位置，这也就是循环数组一个最基本的做法(到达最后一个位置时再回到最开始的位置)，这时判断rear == front。

搞清楚这个之后，实现循环队列就比较简单了.

typedefstruct{int* arr;int front;int rear;int arrSize;} MyCircularQueue;

MyCircularQueue*myCircularQueueCreate(int k){
    MyCircularQueue* obj =(MyCircularQueue*)malloc(sizeof(MyCircularQueue));//多增加一个位置
    obj->arr =(int*)malloc(sizeof(int)*(k+1));
    obj->front = obj->rear =0;
    obj->arrSize = k+1;return obj;}//头尾相等则为空
bool myCircularQueueIsEmpty(MyCircularQueue* obj){return obj->front == obj->rear;}//尾+1等于头则为满
bool myCircularQueueIsFull(MyCircularQueue* obj){return((obj->rear+1)% obj->arrSize)== obj->front;}//插入数据
bool myCircularQueueEnQueue(MyCircularQueue* obj,int value){if(myCircularQueueIsFull(obj)){return0;}
    
    obj->arr[obj->rear]= value;
    obj->rear++;//++后如果==arrSize，让其%arrSize回到0//小于%后值不变
    obj->rear %= obj->arrSize;return1;}//删除数据
bool myCircularQueueDeQueue(MyCircularQueue* obj){if(myCircularQueueIsEmpty(obj)){return0;}//同样的道理，如果++等于arrSize
    obj->front++;
    obj->front %= obj->arrSize;return1;}//返回队头数据intmyCircularQueueFront(MyCircularQueue* obj){if(myCircularQueueIsEmpty(obj))return-1;return obj->arr[obj->front];}//返回队尾数据intmyCircularQueueRear(MyCircularQueue* obj){if(myCircularQueueIsEmpty(obj))return-1;return obj->arr[(obj->rear-1)% obj->N];}voidmyCircularQueueFree(MyCircularQueue* obj){free(obj->arr);free(obj);}

有点难哦