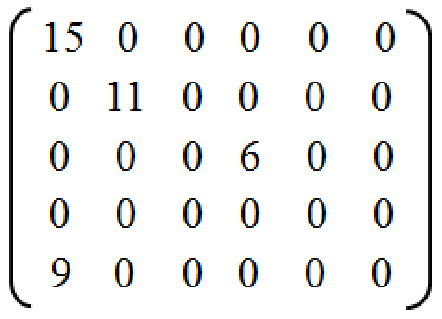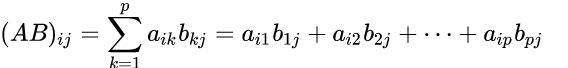【开卷数据结构 】稀疏矩阵

🌺稀疏矩阵

🍁矩阵与稀疏矩阵的定义

---

Q：什么是矩阵

A：数学上，一个矩阵由 m 行 n 列的元素组成，是一个 m 行，n 列的表，m 和 n 是矩阵的维度。一般地，写作 mxn（读作“m乘n”）来指明一个 m 行 n 列矩阵。矩阵的元素个数总计为 mn 个。如果 m 等于 n ，矩阵为方阵。

一般情况下，矩阵的标准存储方式是一个二维数组 a[MAX_ROWS][MAX_COLS] 。利用这种存储方式，可以通过 a[i][j] ，通过行下标，列下标快速找到任意元素的存储位置。

---

Q：什么是稀疏矩阵

A：一个矩阵的绝大部分都为零元素，我们把这种矩阵称为稀疏矩阵。

---

如图：矩阵中只有 2/15 是非零元素，这就是一个标准的稀疏矩阵

---

Q：二维数组储存矩阵的缺点

A：如果一个矩阵中包含很多零元素（是稀疏矩阵），就会浪费大量的存储空间。因此，稀疏矩阵的存储表示只需存储非零元素。

---

Q：稀疏矩阵的存储方式

A：通过对矩阵的分析，我们发现使用三元组 <row,col,value> 能够唯一的刻画矩阵的任意一个元素。这意味者可以使用三元数组来存储表示稀疏矩阵。

💬 代码演示

#define MAX_TERMS 101    //定义最大长度 
typedef struct{
    int col;
    int row;
    int xalue;
}term;
term a[MAX_TERMS];

我们可以用 a[0].row 表示行的数目，用 a[0].col 表示列的数目，用 a[0].value 表示非零元素的总数。其他位置 row 域存放行下标， col 域存放列下标，value 域存放元素值。三元组按照行的顺序排序，并且在同一行内按照列的顺序排序。

稀疏矩阵存储为三元组
行列值a[0]564a[1]0015a[2]1111a[3]236a[4]409

🌺稀疏矩阵的转置

🍁详细思路

为了转置一个矩阵，必须交换它的行和列。也就是说，原矩阵的任意元素 a[i][j] 应该成为其转置矩阵的元素 b[j][i]

---

🍀思路一

依次循环每一列，找到每一列的所有元素并把他们储存在转置矩阵的对应的行上。

//伪代码
for 对于 j 列的所有元素
    把元素<i，j，value>放置在元素<j，i，value>中

💬 代码演示

void transpose(term a[],term b[])
//b是a的转置 
{
    int n,i,j,currentb;
    n=a[0].value;            //元素总数 
    b[0].row=a[0].col;        //b的行数=a的列数
    b[0].co 1=a[0].row;        //b的列数=a的行数
    b[0].value =n;
    if(n> 0) 
    {// 非零矩阵 
        currentb=1;
        for(i=0;i<a[0].col;i++)
        //按a的列转置
            for(j=1;j<=n;j++)
            //找出当前列的所有元素
                if(a[j].col==i)
                {//元素是当前列的，加入b
                    b[currentb]. row=a[j]. col;
                    b[currentb]. col=a[j]. row;
                    b[currentb]. value=a[j]. value;
                    currentb++;
                }
    }
}

---

🍀思路二

首先确定原矩阵中每一列的元素个数，这也就是其转置矩阵中每一行的元素个数。于是就可以得到转置矩阵每行的起始位置，从而，可以将原矩阵的元素依次移到其转置矩阵中的恰当位置。

💬 代码演示

void fast transpose(term a[], term b[])
{
//将a的转置矩阵存放于b中 
    int row terms[MAX_COL], starting pos[MAX_COL]; 
    int i,j, num_cols=a[0].col, num_terms=a[0].value;
    b[0].row=num_cols;b[0].col=a[0].row;
    b[0].value=num_terms;
    if(num_terms>0){//非零矩阵
        for(i=0;i<num_cols;i++)
            row_terms[i]=0;
        for(i=1;i<=num_terms;i++)
            row_terms[a[i]. co]]++;
        starting_pos[0]=1;
        for(i=1;i<num cols;i++)
            starting_pos[i]=starting_pos[i-1]+row_terms[i-l];
        for(i=1;i<=num_terms;i++){
            j=starting_pos[a[i].col]++;
            b[j].row=a[i].col;b[j].col=a[i].row;
            b[j].value=a[i].value;
        }
    }
}

🌺稀疏矩阵的乘法

Q：什么是矩阵乘法

A：设A为 mxp 的矩阵，B为 pxn 的矩阵，那么称 mxn 的矩阵D为矩阵A与B的乘积，记作D=AB，其中矩阵D中的第 i 行第 j 列元素可以表示为：

注意：两个稀疏矩阵的乘积可能不再是稀疏矩阵

---

🍁详细思路

---

我们可以按照行的顺序计算D的元素，把元素存放到正确的位置，这样就不用移动已计算出的元素的位置。一般情况下，必须遍历整个B才能得到第 j 列的所有元素。但是，我们可以先计算 B 的转置，使列元素顺序相续排序，可以避免重复多次遍历整个 B 。

对于找出的 A 的第 i 行和 B 的第 j 列的所有元素，做合并操作就能实现矩阵乘法。

💬 代码演示

void storesum(term a[],int *totald,int row,int column,int *sum)
{//如果 *sum！=0，它的行和列存储位置为 d 中的 *totald+1
    if(*sum)
        if(*tptald<MAX_TERMS)
        {
            d[++*totald].row=row;
            d[*totald].col=column;
            d[*totald].value=*sum;
            *sum=0;
        }
        else{
            fprintf(stderr,"Numbers of terms in product exceeds %d\n",MAX_TERMS); 
            exit(1);
        }
}


void mmult(term a[], term b[], term d[])
//将两个稀疏矩阵相乘 
{
    int i,j,column,totalb=b[0].value,totald=0; 
    int rows_a=a[0].row,cols_a=a[0].col;
    totala=a[0].value;int cols_b=b[0].col;
    int row_begin=1, row=a[1].row, sum=0; 
    int new_b[MAX-TERMS][3];
    if(cols_a!=b[0].row){
        fprintf(stderr,"Incompatible matrices\n"); 
        exit(1);
    }
    fast_transpose(b.new_b);
    //设置边界条件
    a[totala+1].row=rows_a;
    new_b[totalb+1].row=cols_b; 
    new_b[totalb+1].col=0;
    for(i=1;i<=totala;){
        column=new_b[1].row; 
        for(j=1;j<=totalb+1;){
        //将a的行乘以b的列
            if(a[i].row!=row){
                storesum(d,&totald,row,column,&sum);
                i=row_begin;
                for(;new_b[j].row==column;j++)
                    ;
                column=new_b[j]. row;
            }
            else if(new_b[j].row!=column){
                storesum(d,&totald,row,column,&sum); 
                i=row_begin;
                column=new_b[j].row;
            }
            else switch(COMPARE(a[i].col,new_b[j].col)){
                case-1://转到a中的下一项
                    i++;break;
                case 0://添加项，转到a和b的下一项 
                    sum+=(a[i++].value*new_b[j++].value); break;
                case 1://来到b的下一项
                    j++;
            }
    }// for j<=totalb+1 结束循环 
    for(;a[i].row==row;i++)
        ;
    row_begin=i;row=a[i].row;
    }//for i<=totala 结束循环 
    d[0].row=rows_a;
    d[0].col=cols_b;d[0].value=totald;
}