0
0

【数据结构】有妙手、本手、俗手？这7道二叉树题，我打赌你们一个都不会

🌈欢迎来到数据结构专栏~~二叉树oj题

  • (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort🎓
  • 🌍博客主页：张小姐的猫~江湖背景🌍
  • 快上车🚘，握好方向盘跟我有一起打天下嘞！
  • 送给自己的一句鸡汤🤔：
  • 🔥别大声说，要默默做🔥
  • 🙏作者水平很有限，如果发现错误，可在评论区指正，感谢🙏
  • 🎉🎉欢迎持续关注！🎉🎉请添加图片描述

请添加图片描述

7道二叉树面试真题超详剖析

请添加图片描述

💫圣经~《秒杀基础二叉树》

请添加图片描述

💯秒杀大法：

**跳出递归的

条件

（极端条件）➕左右子树的

逻辑关系

➕

遍历方式

**

  • 1️⃣停止继续递归的条件：相等是拿不到结果，记住要去抓不相等
  • 2️⃣左右子树的逻辑关系：要看题目的意思去判断➡️ 左右子树要返回什么样的逻辑关系（eg：||、&&、+、-等）
  • 3️⃣遍历方式：根据题目要求来适配对应的遍历方式

光说不练 假本事，下面我们操刀试试看🔍

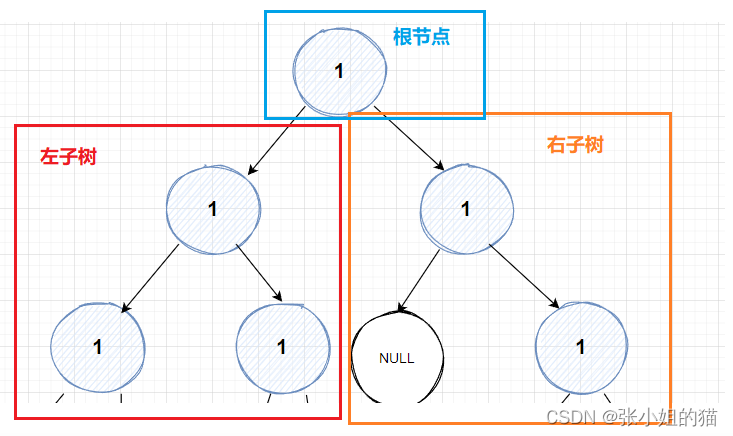
🌍第1️⃣题：单值二叉树【难度：简单】

🏷️力扣地址：🌈965. 单值二叉树

🌍题目描述： 如果二叉树每个节点都具有

相同的值

，那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时，才返回 true；否则返回 false。

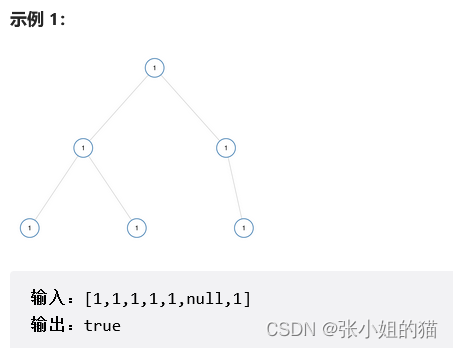
在这里插入图片描述

💫关键思路：

  • ➡️简单来说：在二叉树里所有节点的值都相等
  • 遍历或者递归每个节点进行比较，直到每个节点的值都相等即可

💯圣经秒杀大法：

  • 我们先找到停止继续递归的条件： - 1️⃣当遇到root等于NULL，停止——return true- 2️⃣当子树存在并且子树的值不等于子树的左右子树的值——return false

Mark一下：相等是拿不到结果，记住要去抓不相等。我们想一想相等是不是只能继续递归下去，所以我们要去找不相等。

  • 接着我们找左右子树的逻辑关系：

在这里插入图片描述

  • 我们知道当左右子树都判断完，返回结果为true时才满足单值二叉树- 1️⃣所以我们便知道此题的逻辑关系为&&
  • 这道题的逻辑是：每个节点进行比较，直到每个节点的值都相等，那么是不是先是访问根再左右子树——>前序遍历- 2️⃣每次递归先判断root的值是不是相等，若相等才去访问左右子树，不相等直接return false，不用继续递归下去了，其他的遍历方式都不适合

👆综上：

  • root为NULL、值不相等➕&&➕前序遍历
  • 本质是通过不断递归比较每个节点是否相同【等号有传递性】

💥特别注意：

  • 遍历法：慎用全局变量，最好每次调用的时候都控制一下
  • 树为空时，也满足单值的条件，return true
  • 若左子树有不相等的值，则会直接返回，不需要再访问右子树

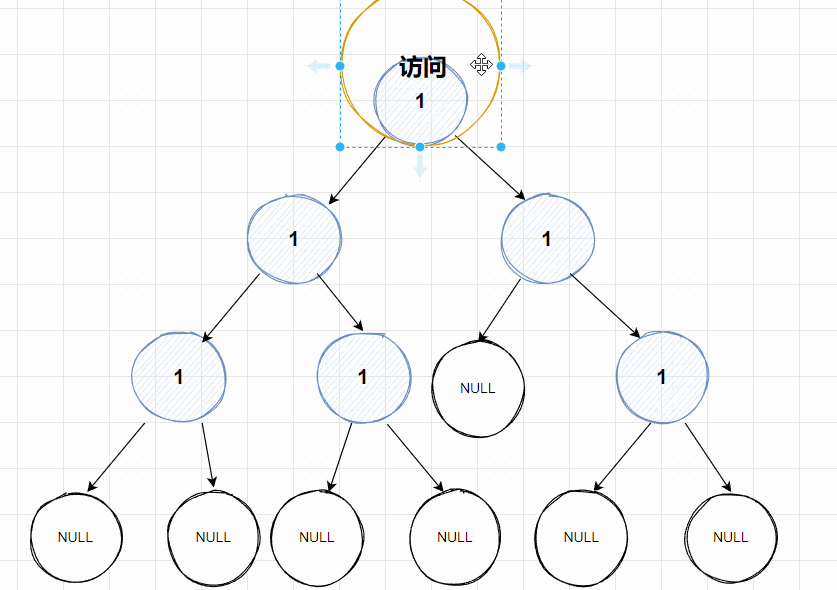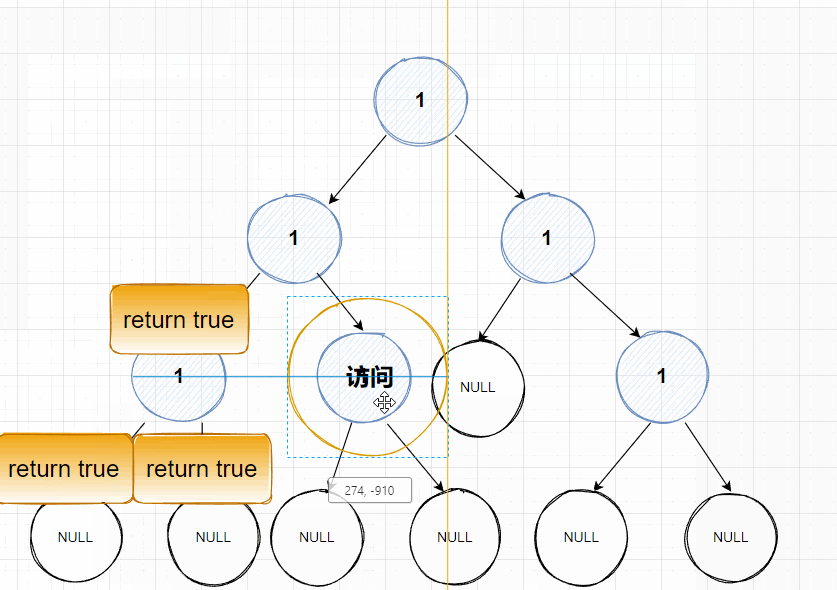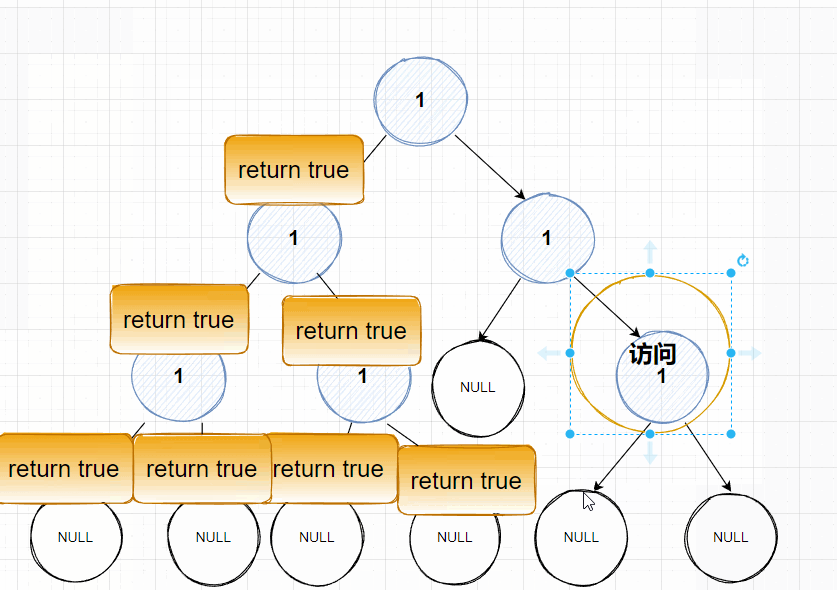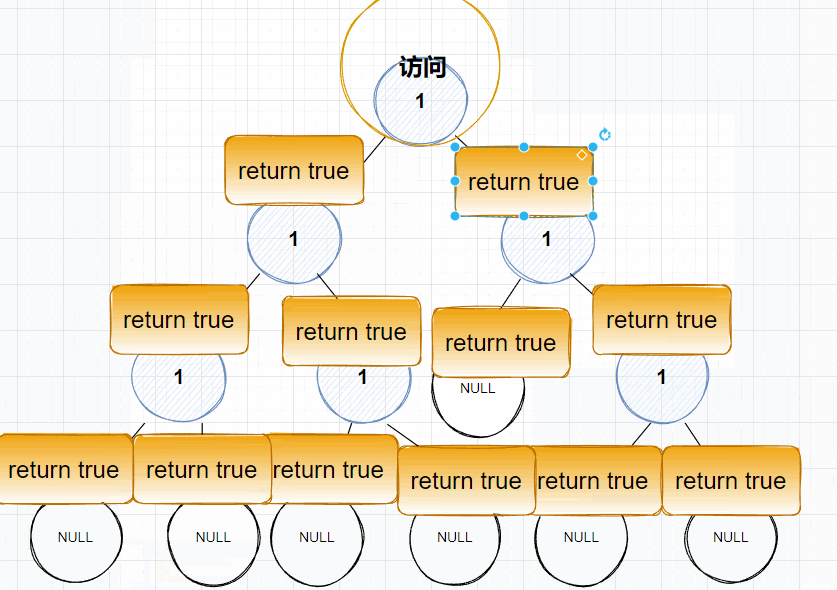
🌠动图解析：👇🏻

请添加图片描述

代码实现💡：
1️⃣遍历法：

bool flag =true;voidPreOrderCompare(structTreeNode* root,int val){if(root==NULL|| flag == false)//如果遇到false就不用继续遍历了return;if(root->val!=val){
        flag=false;return;}PreOrderCompare(root->left,val);PreOrderCompare(root->right,val);}

bool isUnivalTree(structTreeNode* root){if(root==NULL)return true;
    flag=true;//初始全局变量PreOrderCompare(root,root->val);return flag;}

2️⃣递归法

bool isUnivalTree(structTreeNode* root){if(root==NULL)return true;if(root->left &&root->left->val !=root->val)return false;if(root->right &&root->right->val !=root->val)return false;returnisUnivalTree(root->left)&&isUnivalTree(root->right);}

请添加图片描述

🌍第2️⃣题：相同的树【难度：简单】

🏷️力扣地址：🌈100. 相同的树

🌍题目描述：给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

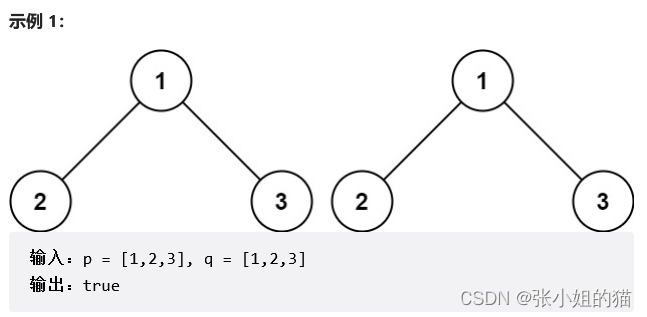在这里插入图片描述🏷️解题关键

  • 要准确的找出四种停止递归的条件并及时的return 相应的true/false

💫关键思路：

  • ➡️ 当走到根节点为空/树本为空，则可证明两棵树相同
  • 若树的结构相同，则再对值进行比较

💯圣经秒杀：

  • 1️⃣当q和p都为空、q空和p非空、q非空和p空、q和p的值不相等四种跳出递归的情况
  • 2️⃣分析得知，我们选择：&&和前序遍历

🌠动图解析：👇🏻

请添加图片描述

ps：动图中的两个访问圈再代码里是

同时进行

的，而且两棵树节点都NULL的时候才

共同返回一个true

代码实现💡：

bool isSameTree(structTreeNode* p,structTreeNode* q){if(q==NULL&& p==NULL)//判断树or根节点都为空return true;if(q==NULL|| p==NULL)//判断p、q的结构是否相同return false;if(q->val != p->val)//结构相同后，才是进行值的比较return false;returnisSameTree(p->left,q->left)&&isSameTree(p->right,q->right);}

请添加图片描述

🌍第3️⃣题：对称二叉树【难度：简单】

🏷️力扣地址：🌈101. 对称二叉树

🌍题目描述：给你一个二叉树的根节点 root ， 检查它是否轴对称。

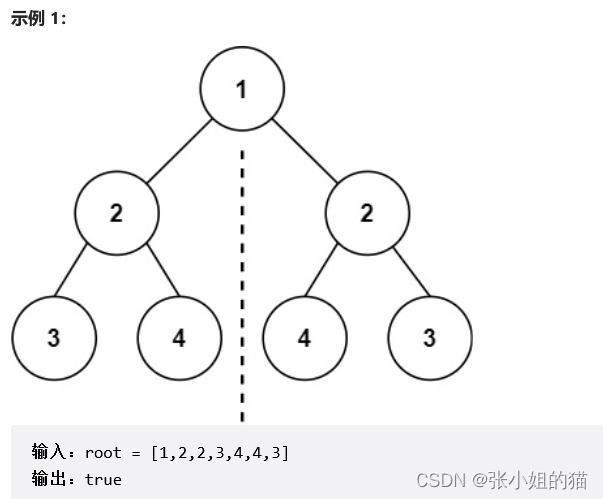
在这里插入图片描述

💫关键思路：

  • ➡️ 本题目可复用上题的思路
  • 只需把树拆开看成左子树、右子树两棵树，再复用相同树的代码即可

💥特别注意：

  • 注意对称的问题 - 左树的左子树是和右树的右子树相比较的- 左树的右子树是和右树的左子树相比较的

代码实现💡：

bool issam(structTreeNode* q,structTreeNode* p){if(p ==NULL&& q ==NULL)return true;if(p ==NULL|| q ==NULL)return false;if(q->val != p->val)return false;returnissam(q->left,p->right)&&issam(q->right,p->left);}
bool isSymmetric(structTreeNode* root){if(root==NULL)return true;returnissam(root->left,root->right);}

🛫难度提升

🌍第4️⃣题：另一棵树的子树【难度：中等】

🏷️力扣地址：🌈572. 另一棵树的子树

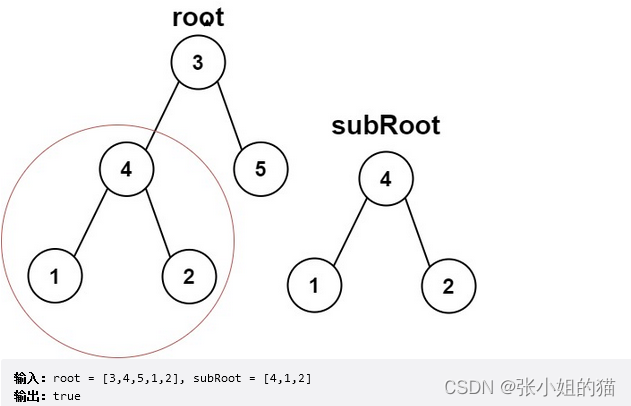
🌍题目描述：给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

  • 二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

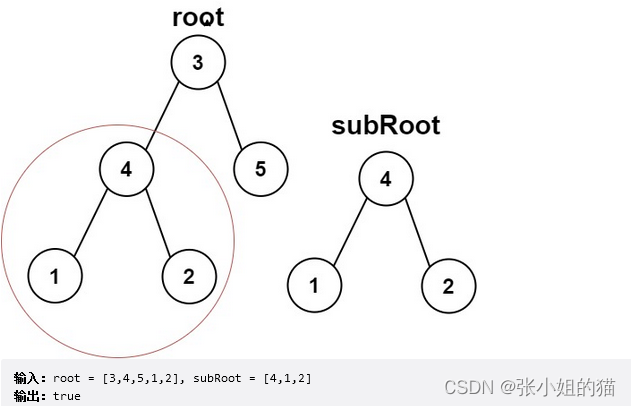
在这里插入图片描述
💫关键思路：

  • 原树中的所有子树找出来和SubRoot进行比较一下就可以了

💥特别注意：：

  • 判断 t 是否和树 s 的任意子树相等。那么就转化成🌈100. 相同的树 即可，这个题的做法就是在 s 的每个子节点上，判断该子节点是否和 t 相等。
  • 判断两个树是否相等的三个条件是与的关系，即：- 1️⃣当前两个树的根节点值相等；- 2️⃣并且，s 的左子树和 t 的左子树相等；- 3️⃣并且，s 的右子树和 t 的右子树相等
  • 而判断 t 是否为 s 的子树的三个条件是或的关系，即：- 1️⃣ 当前两棵树相等；- 2️⃣ 或者，t 是 s 的左子树；- 3️⃣ 或者，t 是 s 的右子树。

我们发现：判断 是否是相等的树 与 是否是子树 的代码简直是对称美啊~
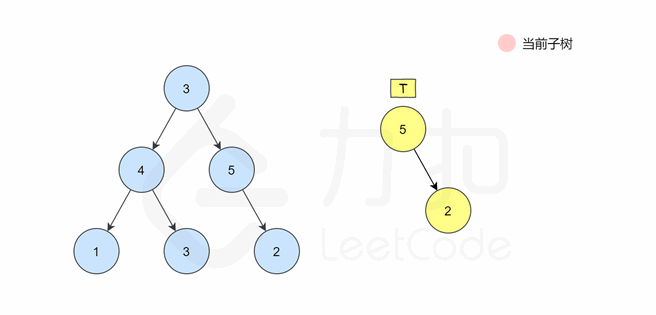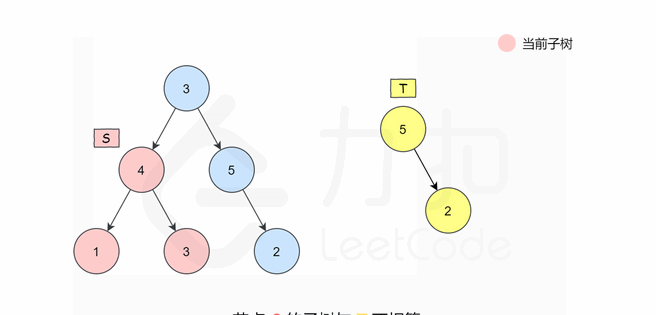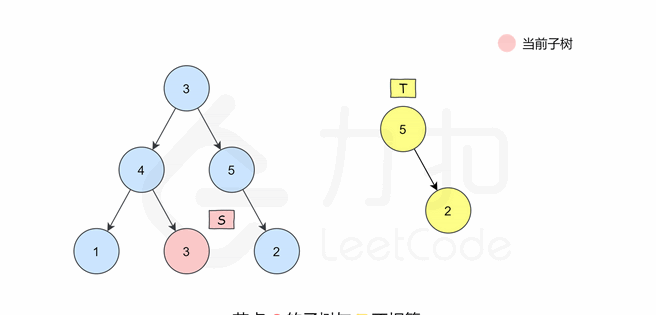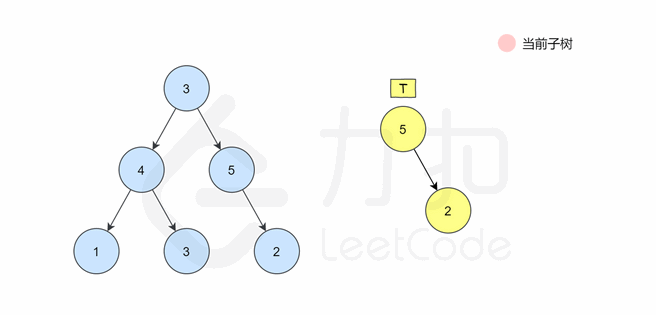
请添加图片描述

🌠动图解析：👇🏻

请添加图片描述

代码实现💡：

bool isSameTree(structTreeNode* p,structTreeNode* q){if(p ==NULL&& q ==NULL)return true;if(p ==NULL|| q ==NULL)return false;if(p->val != q->val)return false;returnisSameTree(p->left,q->left)&&isSameTree(p->right,q->right);}

bool isSubtree(structTreeNode* root,structTreeNode* subRoot){if(root==NULL)return false;//遍历跟，和所有的子树都比较一遍if(isSameTree(root,subRoot))return true;//但凡有一个相等就认为是我的子树returnisSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);}

🌍第5️⃣题：二叉树的前序遍历【难度：中等】

🏷️力扣地址：🌈144. 二叉树的前序遍历

同学们卡到这里心想：二叉树的前序不就那三步吗？好戏还在后头

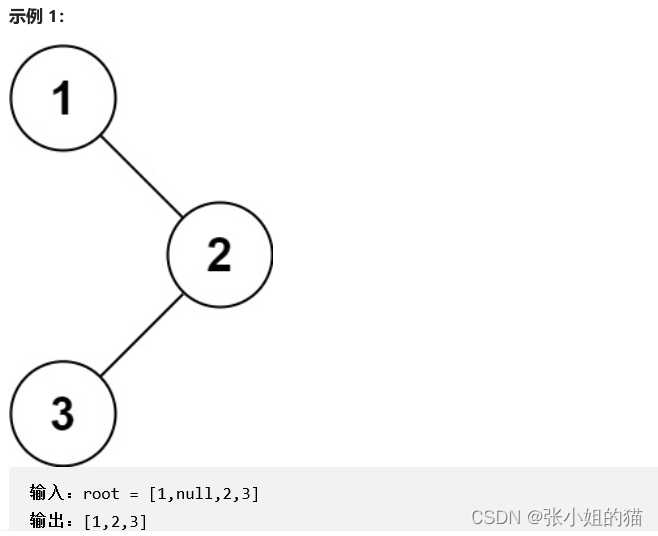
🌍题目描述：给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

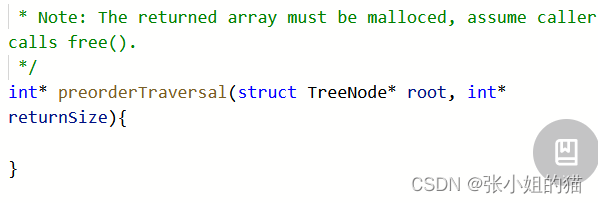
- 二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

题目要求的不是要把前序的值打印一下，而是把前序的结果放在

malloc的数组

里

  • returnSize是输出型参数，与root不同，要解引用，外面要拿取数据

在这里插入图片描述

💫关键思路：

  • 先把TreeSize函数输出给returnSize，然后malloc一个数组a，下标为i
  • 定义 preorder 表示当前遍历到 root 节点的答案。按照定义，我们只要首先将 root 节点的值、数组、下标i加入答案，然后递归调用 preorder(root->left，a,i) 来遍历 root 节点的左子树，最后递归调用 preorder(root->right,a,i) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

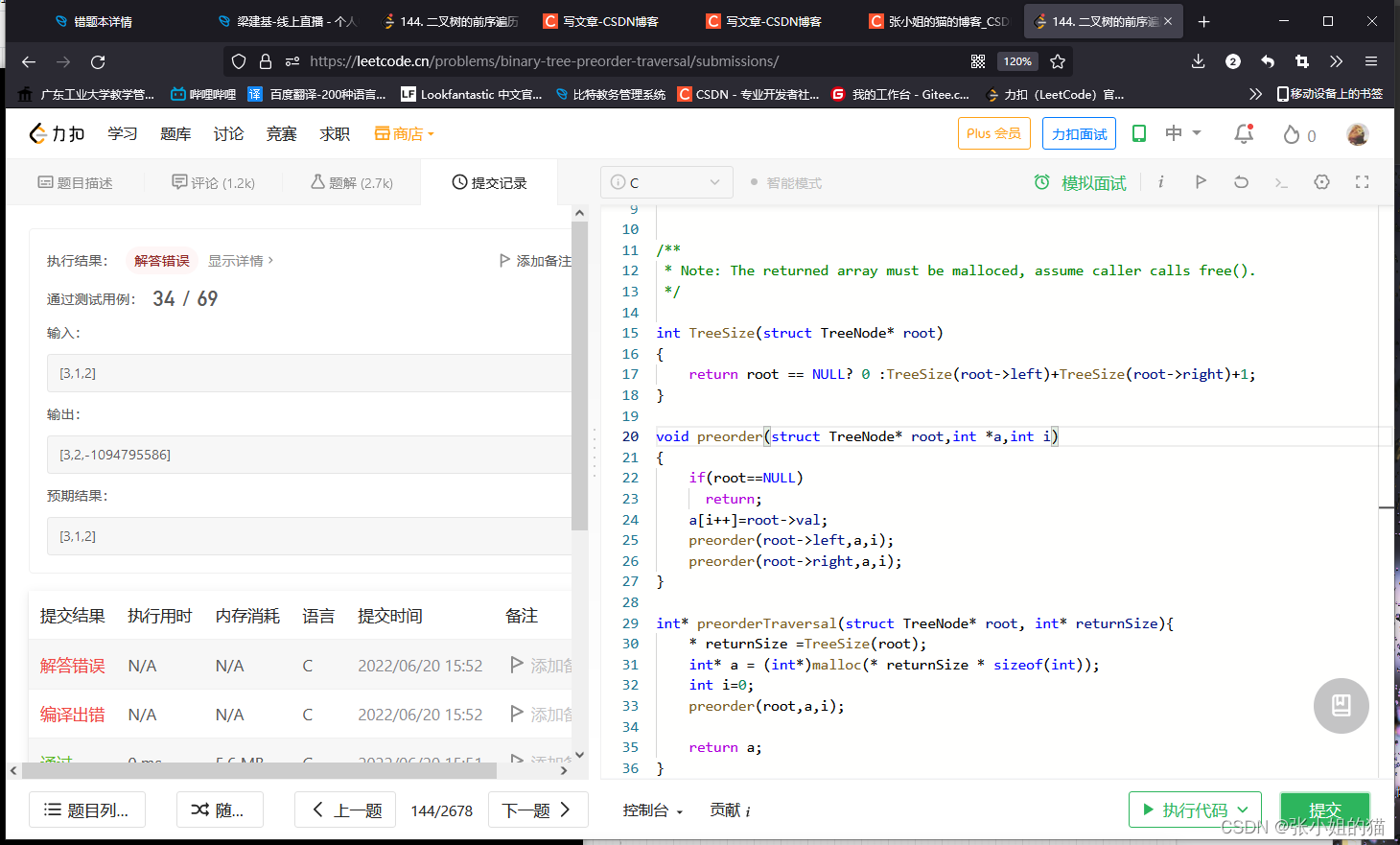
❌意料之外报错：

在这里插入图片描述

💥特别注意：

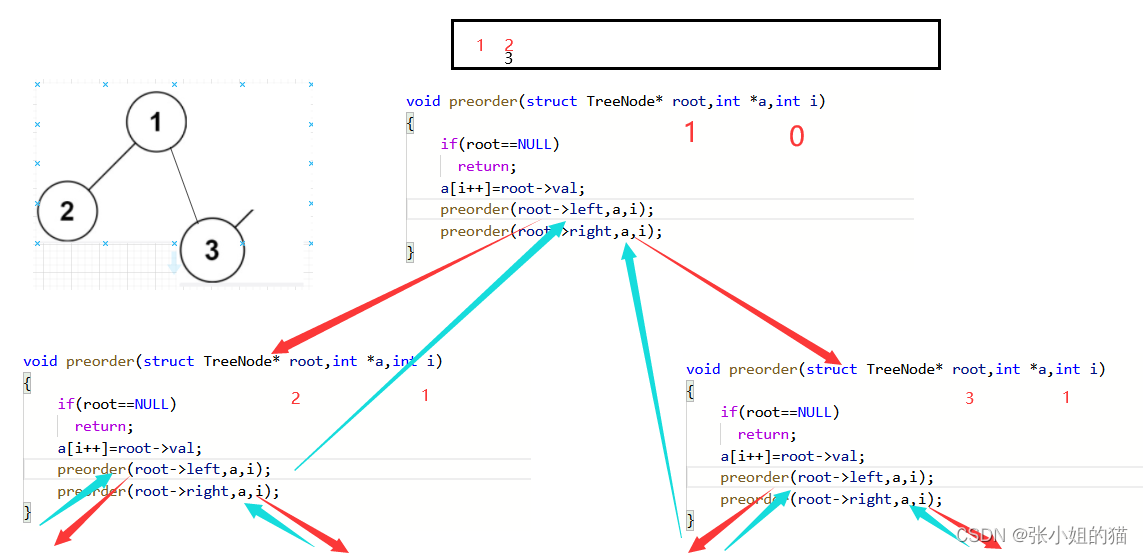
  • 当root递归左子树的时候，左子树的i++，不影响root的i(因为i是局部变量)，所以左右子树的i都相同，放进数组里会放在同一个位置。
  • 也就说：不是一个i在往后走

在这里插入图片描述

对此我们可以传

i的地址

，

解引用i

，使得只有

一个i

走完全程。

代码实现💡：

intTreeSize(structTreeNode* root){return root ==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;}voidpreorder(structTreeNode* root,int*a,int*pi){if(root==NULL)return;
    a[(*pi)++]=root->val;preorder(root->left,a,pi);preorder(root->right,a,pi);}int*preorderTraversal(structTreeNode* root,int* returnSize){* returnSize =TreeSize(root);int* a =(int*)malloc(* returnSize *sizeof(int));int i=0;preorder(root,a,&i);return a;}

🌍第6️⃣题：二叉树遍历 【难度：中等】

🏷️地址：🌈KY11 二叉树遍历

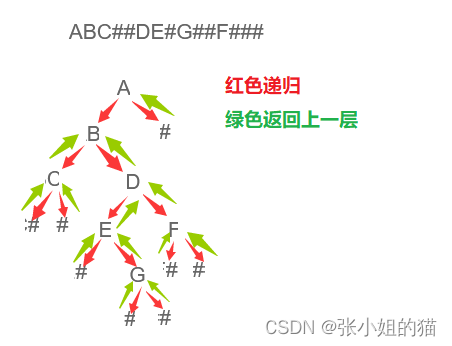
🌍题目描述：编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的

先序遍历字符串

： ABC##DE#G##F### 其中“

#

”表示的是

空格

，空格字符代表空树。建立起此二叉树以后，再对

二叉树进行中序遍历

，

输出

遍历结果。

  • 输入描述： 输入包括1行字符串，长度不超过100。
  • 输出描述： 可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

在这里插入图片描述

🌠画图解析：👇🏻

在这里插入图片描述

💫关键思路：

  • 使用数组的值依次按先序遍历，分治思想，递归构建二叉树，构建二叉树先malloc出根节点然后再构建左子树，右子树即可。
  • 字符串需要构建之后str【（*pi）++】不断找到下一个字符，当指向‘#’代表到了空节点了完成返回NULL即可，
  • 若非空，则开创一个节点，递归构建左右子树

💥特别注意：

如果有不理解的地方，可以去画递归展开图多尝试理解

代码实现💡：

#include<stdio.h>#include<stdlib.h>#include<assert.h>typedefchar BTDataType;typedefstructBinaryTreeNode{
    BTDataType data;structBinaryTreeNode* left;structBinaryTreeNode* right;}BTNode;

BTNode*BuyNode(BTDataType x){
    BTNode* node =(BTNode*)malloc(sizeof(BTNode));assert(node);

    node->data = x;
    node->left =NULL;
    node->right =NULL;return node;}
BTNode*CreateTree(char*str,int*pi){if(str[*pi]=='#'){(*pi)++;returnNULL;}
    BTNode*root=BuyNode(str[(*pi)++]);
    
    root->left=CreateTree(str, pi);
    root->right=CreateTree(str, pi);return root;}voidInOrder(BTNode*root){if(root==NULL)return;InOrder(root->left);printf("%c ",root->data);InOrder(root->right);}intmain(){char str[100];scanf("%s",str);int i=0;
    BTNode* root =CreateTree(str,&i);InOrder(root);}

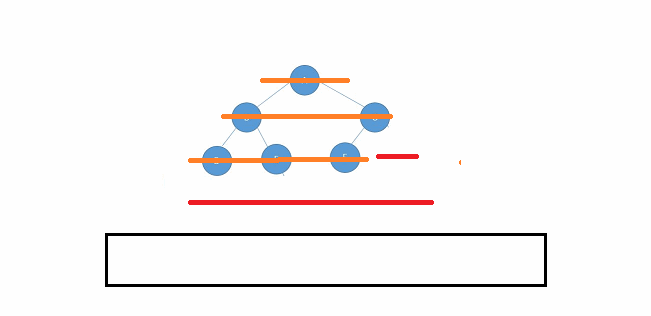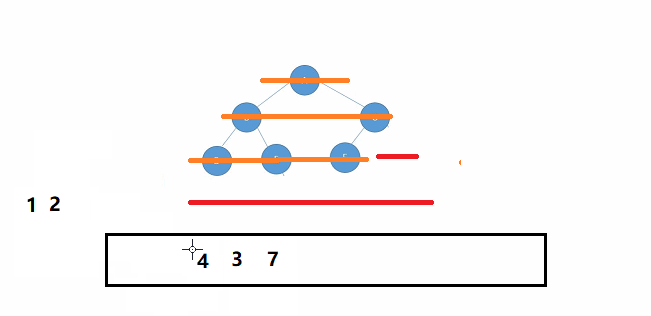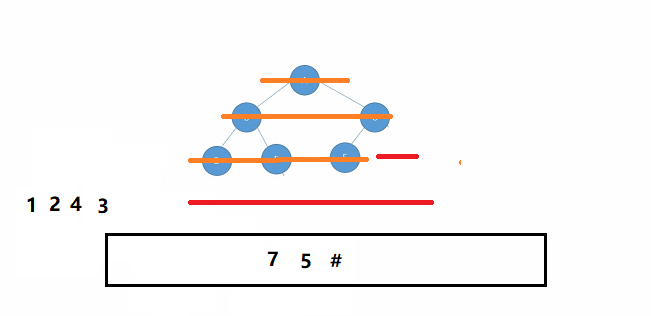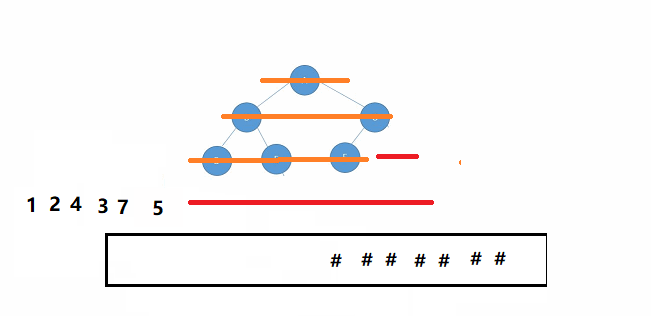
🌍第7️⃣题：判断二叉树是否为完全二叉树 【难度：中等】

🌈科普：

  • 完全二叉树也就是没有满的满二叉树，它的节点在每一层一定是连续分布的。如果出现哪一层中两个非空节点间隔一个空节点，那一定不是完全二叉树。如下图所示👇🏻

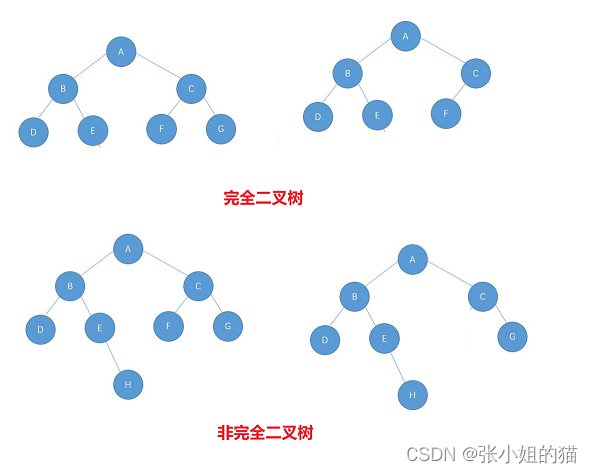
在这里插入图片描述

假设这棵完全二叉树有K层，因此我们可以总结一下完全二叉树的规律：

  • 前K-2层：每个节点都有两个孩子，节点饱和
  • 前K-1层：节点肯定是饱和的—>到达了最大值
  • 第K-1层：不一定所有的节点都有孩子节点，如果有孩子节点，至少要是左孩子节点,有可能出现不饱和节点

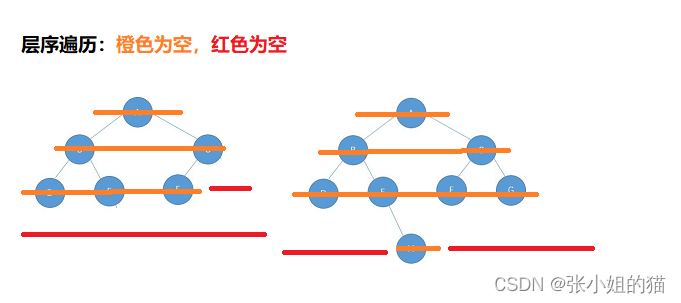
🌠动图解析：👇🏻

请添加图片描述

💫关键思路：
由于完全二叉树在每一层非空节点都是一个接一个连续分布的，不可能出现两个非空节点之间交叉一个空节点，因此：

  • 我们可以通过层序遍历从上往下，从左往右将每一个节点（包括非空节点）都放到队列里
  • 在出队列的过程中，如果遇到空节点，则跳出循环
  • 跳出循环后，然后再判断队列中剩下的元素是否有非空节点：- 有非空节点：非完全二叉树；- 没有非空节点（全是空节点）：完全二叉树。

在这里插入图片描述

代码实现💡：

intBinaryTreeComplete(BTNode* root){
    Quene q;QueneInit(&q);if(root){QuenePush(&q, root);}while(!QueneEmpty(&q)){
        BTNode* front =QueneFront(&q);QuenePop(&q);if(front){QuenePush(&q, front->left);QuenePush(&q, front->right);}else{//遇到NULL ，跳出层序遍历break;}}//1、如果后面全是NULL，则是完全二叉树//2、如果空后面还有非空，则不是完全二叉树while(!QueneEmpty(&q)){
        BTNode* front =QueneFront(&q);QuenePop(&q);if(front){QueneDestroy(&q);return false;}}QueneDestroy(&q);return true;}

💥特别注意：
我们发现这里：明明pop掉了节点，front为什么还能继续
在这里插入图片描述

  • 首先我们要知道队列原本存的就是树节点的指针
typedefstructBinaryTreeNode* BTDataType;
  • BTNode* front = QueneFront(&q)——>指向的是队列的data、相当于front指向节点1，也就变相保存了队列数据
  • pop掉的是头队列，但数据我们保存下来了，没有丝毫影响

请添加图片描述

ps：return之前都要Destroy一下，不然会内存泄漏

📢写在最后

  • 能看到这里的都是棒棒哒🙌！
  • 想必二叉树也算是数据结构中比较难🔥的部分了，如果认真看完以上部分，肯定有所收获。
  • 接下来我还会继续写关于📚《栈和队列》等…
  • 💯如有错误可以尽管指出💯
  • 🥇想学吗？我教你啊🥇
  • 🎉🎉觉得博主写的还不错的可以一键三连撒🎉🎉在这里插入图片描述
标签： 数据结构 算法 c语言
本文转载自: https://blog.csdn.net/qq_42996461/article/details/124754656
版权归原作者 张小姐的猫 所有， 如有侵权，请联系我们删除。
登录后发布评论

“【数据结构】有妙手、本手、俗手？这7道二叉树题，我打赌你们一个都不会”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

机器人技术在安全领域的重要作用

安全学习记录——网络篇（一）

图腾柱PFC：HP1010为您的电动两轮车之旅提供绿色，高效，安全的动力

单元测试数据库回滚问题

这才是单元测试，之前我们都错了

【C语言基础】：字符函数和字符串函数

ChatGPT-Next-Web SSRF漏洞+XSS漏洞复现(CVE-2023-49785)

文章导航