生产企业原材料订购与运输的研究-数据处理课程设计

目录

摘要

生产企业原材料订购与运输的研究
Yeats_Liao*
（XXXX学院 XXX学院 XXXX XXXXXX）
摘要：本文就生产企业在原材料的订购与运输中订货量与供货量之间的数据进行分析。根据240周内的供货商们的供货量和企业的订货量进行相关的数据统计并建立数学模型，根据不同的方案要求，建立模型，确定其最优订购和转运方案。如果供应商的原材料供应稳定性波动大，表示该企业生产保障低。在此基础上利用评价算法，排序评分50家最重要的供应商。
为该企业制定未来 24 周每周最经济的原材料订购方案，以量化分析结果作为参考，考虑50家最重要的供应商产量的限制、企业能否保持未来两周的产量以及自身的生产因素的约束，建立0-1规划模型，得出制定 24 周的原材料计划以满足该企业 48 周安排生产方案。在最优订购方案的基础上，对转运商损耗强度指标建立评价模型，考虑损耗最少的转运方案，分析运输损耗率方差、损耗率均值、有订单周数、订单占比量，得出按每周选择损耗最少的转运商。
本文在制定新的订购方案及转运方案并分析方案的实施效果中，使用Jupyter Notbook、Lingo、Excel等软件对模型进行分析求解，建立了迭代模型，增加了新方案的精准性与模型的严谨性。并将遗传算法应用于订购方案与转运方案的寻优过程中，并对符合实际情况的方案进行了推广。

关键词：供货强度指标 0-1规划 转运商损耗强度 遗传算法 寻优算法

Research on Ordering and Transportation of Raw Materials in Manufacturing Enterprises
Yeats_Liao*
（XXXX学院 XXX学院 XXXX XXXXXX）
Abstract: This article analyzes the data between the order quantity and the supply quantity in the ordering and transportation of raw materials by the manufacturer. According to the supplier’s supply volume and the company’s order volume within 240 weeks, relevant data statistics and mathematical models are established. According to different program requirements, the model is established to determine the optimal ordering and transshipment program. If the supplier’s raw material supply stability fluctuates greatly, it means that the company’s production guarantee is low. On this basis, the evaluation algorithm is used to rank and score the 50 most important suppliers.
Develop the most economical weekly raw material ordering plan for the company in the next 24 weeks, take the quantitative analysis results as a reference, consider the output restrictions of the 50 most important suppliers, whether the company can maintain the output in the next two weeks, and its own production factors. Constraint, establish a 0-1 planning model, and draw a 24-week raw material plan to meet the company’s 48-week production plan. On the basis of the optimal ordering plan, an evaluation model is established for the loss intensity index of the transshipment company, and the transshipment plan with the least loss is considered. Zhou chooses the forwarder with the least loss.
In this paper, in formulating the new ordering plan and transshipment plan and analyzing the implementation effect of the plan, the model is analyzed and solved using software such as Jupyter Notbook, Lingo, Excel, etc., and an iterative model is established, which increases the accuracy of the new plan and the rigor of the model. . The genetic algorithm is applied to the optimization process of the order plan and the transshipment plan, and the plan that conforms to the actual situation is promoted.
Keywords: Supply intensity index 0-1 planning transporter loss intensity genetic algorithm optimization algorithm

1 引言

某生产企业所用原材料总体可分为A，B，C三种类型。该企业每年按48周安排生产，需要提前制定24周的原材料订购和转运计划，即根据产能要求确定称为供应商和相应订货量，确定转运商并委托其将供应商每周的供货量转运到企业仓库。

供应商实际供货量可能与订货量不匹配。该企业要尽可能保持不少于满足两周生产需求的原材料库存量来保证正常生产的需要，企业对供应商实际提供的原材料总是全部收购。转运过程中原材料会有损耗。实际中A类和B类原材料的采购单价分别比C类原材料高20%和10%，三类原材料运输和储存的单位费用相同。

问题一对402家供应商的供货特征进行量化分析，建立反映保障企业生产重要性的数学模型并确定50家最重要的供应商。问题二分析该企业应至少选择多少家供应商供应原材料才可能满足生产的需求，为该企业制定未来24周每周最经济的原材料订购方案，并制定损耗最少的转运方案。对订购方案和转运方案的实施效果进行分析。

2 规划问题说明

规划问题主要有以下三个部分：
1．决策变量

可以看到, 在供应商阶段, 每家供应商每周供货多少是我们的决策变量, 在运转商阶段, 0-1规划问题, 每家供应商选择哪家运转商进行运转也是我们的决策变量. 其实, 设完这么多未知数, 我们的A,B,C的量到底是多少已经表达出来了, 不需要额外假设。

2．目标函数

由于在本题中, 由于生产的量已经确定了, 就是2.82万立方米的产品.目标函数肯定是成本最低, 当然, 在后续题目中会出现更多的目标函数, 包括多目标规划问题等。

3．约束条件

我们看一下上面写过的约束条件, 做个总结:
(1) 企业对于供货商的原材料, 也就是供货量必须全部收取.
(2) 企业的库存要保持不少于满足两周生产需求的原材料库存量
(3) 一家供应商每周的原材料由一家转运商运输
(4) 每家转运商的运输能力为6000, 也就是说, 如果还能把每个供应商的供货量设出来, 那么矩阵相乘, 得到每家转运商的运输总额, 需要小于等于6000.

3 问题重述

3.1 问题分析

对问题一的分析，附件1为该企业近5年402家原材料供应商的订货量和供货量数据。分析数据，建立订货量模型[1]，考虑供货达标率、周供货量均值、供货量方差、企业订货周数来构建供货强度指标，以此反映保障企业生产的重要性，根据订货量与供货量函数关系以及附件1已知的数据构建方程组来求解。如果供应商的原材料供应稳定性波动大，表示该企业生产保障低。在此基础上利用评价算法，排序评分50家最重要的供应商作为结果。

对问题二的分析，货物分为订购过程，即确定供应商、每周原材料订货量；转运过程即确定转运商、其每周转运原材料供货量。首先要求为企业选择最少的供应商以达到两周生产需求。以问题一作为参考，考虑50家最重要的供应商产量的限制、企业能否保持未来两周的产量以及自身的生产因素的约束。建立选择模型[2]如0-1规划[3]模型分析建立订购方案[4]，在此基础上预测结果按每周选择损耗最少的转运商。

3.2 数据说明

供应商：原材料供应商；
订货量：原材料订购数量；
转运商：第三方物流公司；
供货量：原材料供货数量；
损耗率：损耗量占供货量的百分比；
接收量：转运商实际运送到企业仓库的原材料数量。

附件1的数据说明

(1)企业的订货量：第一列为供应商的名称；第二列为供应商供应原材料的类别；第三列及以后共240列为企业向各供应商每周的订货量（单位：立方米）；数值“0”表示相应的周（所在的列）没有向供应商（所在的行）订货。

(2)供应商的供货量：第一列为供应商的名称；第二列为供应商供应原材料的类别；第三列及以后共240列为各供应商每周的供货量（单位：立方米）；数值“0”表示相应的周（所在的列）供应商（所在的行）没有供货。

附件2的数据说明

第一列为转运商的名称，第二列及以后共240列为每周各转运商的运输损耗率（%）；即损耗率= (供货量-接受率)/ 供货量x 100%[5]；数值“0”表示没有运送。

3.3 模型假设

(1)假设C单位立方米成本为1。
(2)假设企业在第一周初始时原材料库存量为0。
(3)假设一家供应商每周供应的原材料由一家转运商运输。
(4)假设对题目附录所给的数据统计均有效。
(5)假设企业要保持不少于满足两周生产需求的原材料库存量，为当前周与下一周生产需求量[6]。
(6)假设企业当周订货能够当周送达。

3.4 符号说明

各符号及其含义见表1：
表 1 符号说明
Tab.1 Symbol description
符号含义I供货强度指标i周数j供应商IDk转运商IDx订货量y供货量v转运商接受量u转运商供货量A材料A的供货量B材料B的供货量C材料C的供货量A_i第i家供应商材料A的供应量B_i第i家供应商材料B的供应量C_i第i家供应商材料C的供应量A_ij材料A的真实供货量B_ij材料B的真实供货量C_ij材料C的真实供货量P_ij周供货稳定率M_ij供货达标率J_ij周供货量均值D_ij供货量方差D_i企业有订货的周数N满足最少供应商家的数量S转运商损耗强度评分值T转运接受量T_ik损耗率Q最大供货量U产能提升指标E订单占比量Z原材料最优比个数α供货达标率权重α∈(0，1)β供货量方差权重β∈(0，1)γ周供货量均值权重γ∈(0，1)δ企业有订货的周数权重δ∈(0，1)λ周供货量真实均值权重λ∈(0，1)μ供应商最大周供应量权重μ∈(0，1)

4 实验及分析

4.1 问题一模型的建立与求解

1．数据的统计和处理

(1)原材料供应商数量对比

针对供货商的供货特征进行量化分析[7]，对A、B、C类原材料供应商数量分类建立数学规划模型[8]，x轴和y轴分别为原材料类别与供应商总量，A、B、C类分别有145、134、122家供应商，总供应商402家，如下图1所示：

图 1 原材料供应量分类对比
Fig.1 Comparison of raw material supply by classification

(2)分析供应商周供应量

选取S001-S003供应商，建立周供应量分布， x轴和y轴分别为周数与供应材料量，如下图2所示：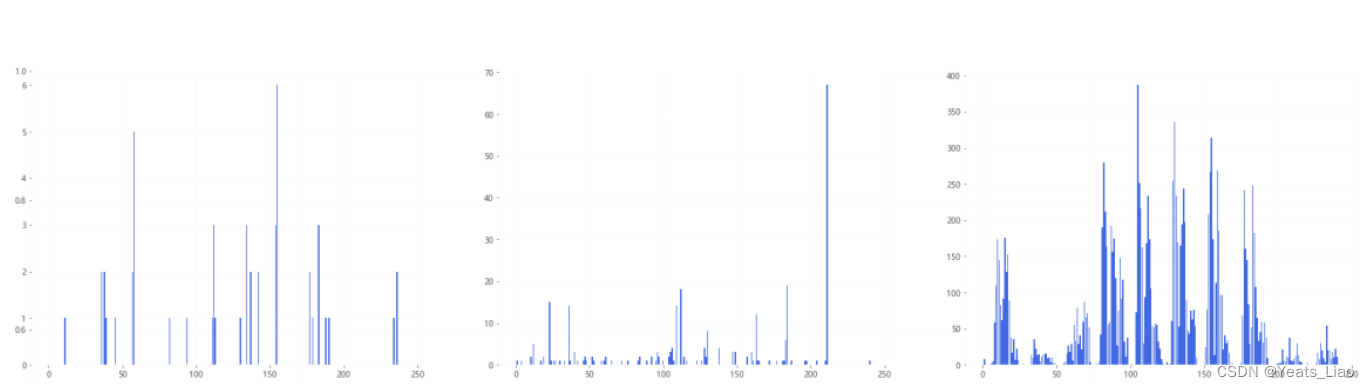

图 2 S001-S003供应商周供应量分布
Fig.2 Weekly supply distribution of S001-S003 suppliers

(3)周订单与供货总量的统计

针对周订单总量与供货总量进行统计分析，为建立反映保障企业生产重要性的数学模型，我们需要分别统计周供货量与周订单量数据，左为周订单量统计图，右为周供货量统计图，如下图3所示：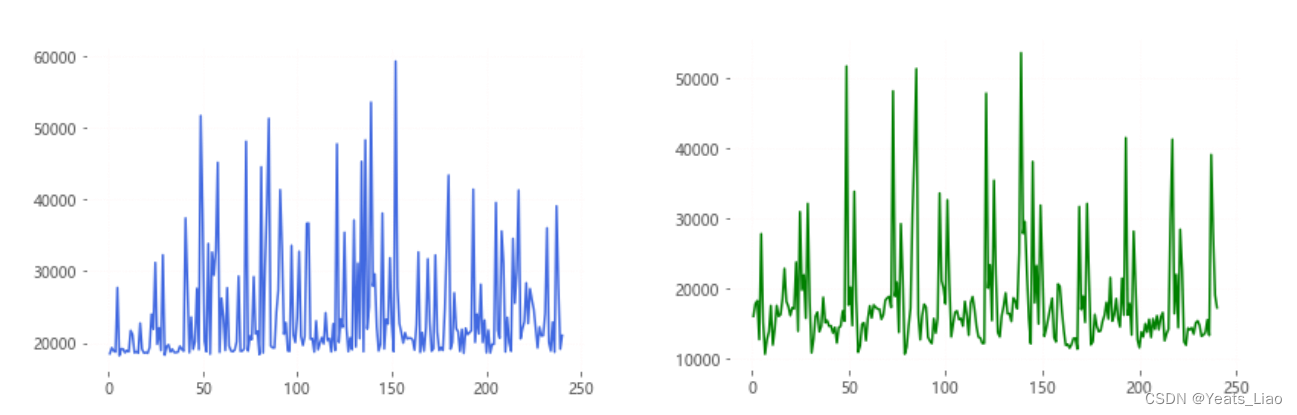

图 3 周订单与供货总量的统计图
Fig.3 Statistics chart of weekly orders and total supply

建立重叠型数值对比图，从而直观反映供需差距，如下图4所示：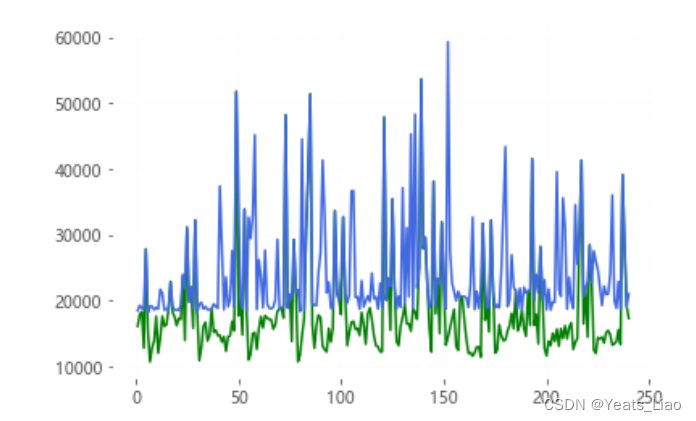

图 4 重叠型数值对比图
Fig.4 Comparison of overlapping numerical values

2．模型的建立

(1)周供货稳定率模型的建立

建立原材料每周订货量比例模型(左)、原材料每周供货量比例模型(右)，得出企业订货量周占比与企业供货量周占比，如下图5所示：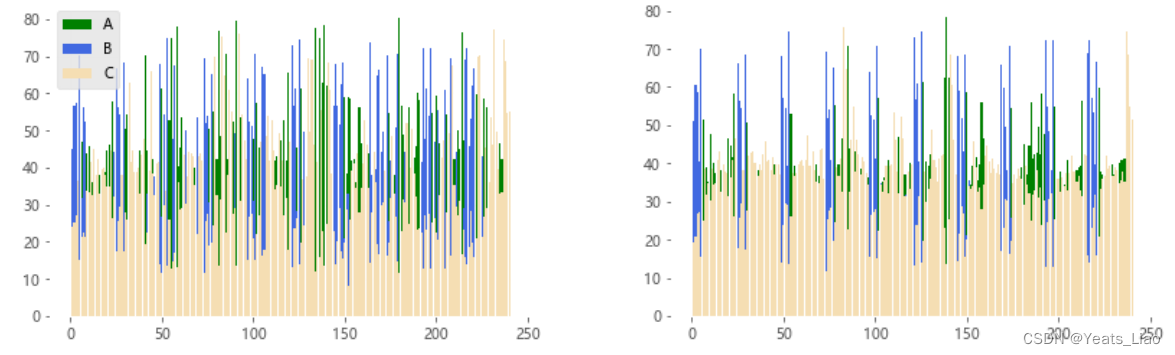

图 5 原材料周订货量比例模型(左)、原材料周供货量比例模型(右)
Fig.5 The ratio model of weekly order quantity of raw materials (left) and the ratio model of weekly supply quantity of raw materials (right)

通过构建的比例模型，考虑每周供货稳定性，计算周供货稳定率=周供货量/周订货量，周供货稳定率P_ij：

P_ij=y_ij/x_ij     

(2)供货达标率

建立供货达标率模型，即当周供货量大于或等于周订货量时，记为该次供货达标P^*，计算供货达标率=供货达标次数/总供货次数，供货达标率M_ij：

M_ij=|p_ij^*|/n    

(3)周供货量均值

周供货量均值即总供货量/周数，平均每周供应商供货量J_ij：

J_ij=(∑▒y_ij )/n    

(4)供货量方差

供货量方差用来统计供货量数据时离散程度的度量。根据variance定理[9]可知 D_ij：

D_ij=(∑▒〖(x_ij-y_ij)〗^2)/n    

(5)企业有订货的周数

对企业的订货量数据进行分析，统计240周中企业有订货的周数D_i。

(6)供货强度指标模型的建立

对供货强度建立评价模型，以分析供应商保障企业生产重要性。对供货特征进行量化分析，根据附件1进行数据分析与处理，计算供货量总量数统计，评估每周企业的订货量与供应商的供货量的值作为供货强度指标。

根据附件1给出该企业近5年402家原材料供应商的订货量和供货量数据，其中供货强度权重(α+β+γ+δ)=1，通过加权[10]供货达标率、周供货量均值、供货量方差、企业订货周数来构建供货强度指标I：

I=αM_ij+βD_ij+γJ_ij+δD_i

展开得：

I=α |p_ij^*|/n+β (∑▒〖(x_ij-y_ij)〗^2)/n+γ (∑▒y_ij )/n+δD_i

根据公式可知，供货强度指标由供货达标率、周供货量均值、供货量方差、企业订货周数来权制决定，此模型指数用来评价建立反映保障企业生产的重要性。

3．模型的求解

根据公式(6)可求解每家供应商供货强度I，排名得出50家最重要的供应商，记录得到下表2：
表2 50家最重要的供应商
Tab.2 The 50 most important suppliers
排名供应商ID排名供应商ID1S17826S0662S17427S0753S07628S0534S23729S3385S17530S0506S22131S1497S16932S3928S09833S1399S23934S30710S32435S08811S19736S31012S21337S10613S20238S37614S37439S03615S06440S02516S09241S15717S20642S26618S11343S14019S25344S33220S17245S26921S03046S08622S34247S15223S00748S25624S14149S37925S06750S314
模型求解构建50家最重要的供应商供货强度指标值，如下图6所示：

图6 50家最重要的供应商供货强度指标值
Fig.6 The supply intensity index values of the 50 most important suppliers

4.2 问题二模型的建立与求解

1．数据的统计和处理

(1)统计供应商最大周供应量

货物订购过程即确定供应商、每周原材料订货量，为达到两周生产需求选择货物达标率前50供应商，问题一作为参考统计供应商最大周供应量O ，统计如表3所示：
表 3 供应商最大周供应量
Tab.3 Maximum weekly supply of suppliers
供应商ID最大周供应量O供应商ID最大周供应量OS17814 S0668S1749 S07530S0765S0537S23712S3382081S1759S0508S2219S14911S1698S39211S09810S13910207S2399S3079385S32412S08810S19711S31013S2134S1066S20210S3767S37423695S0369S06410S0258S0929S1578S2065S26639S11311S14021293S25314S332125S1726S2696S03026S0861265S34216S15210S007155S25611S14112S37955S0674S31440
(2)周供货量真实均值

每周有存在订单量与供应量都为零的情况，只使用周供货量均值无法作为供货量参考条件，计算真实均值，去除都为零的情况。周供货量真实均值k_ij：

k_ij=(J_ij/D_i)×240

(3)供应商真实供货量

根据最大周供应量、周供货量真实均值构建供应商真实供货量Y：
其中(λ+μ)=1

Y=λK_ij+μO

设定供应商真实供货量Y，最大周供货量占比40%、周供货量真实均值占比60%，计算得出结果如表4：
表 4 供应商真实供货量
Tab.4 The actual supply of suppliers
供应商ID原材料类别真实供货量Y供应商ID原材料类别真实供货量YS178A9.817391S066A5.892958S174B6.489764S075B19.15556S076C3.744554S053B5.1625S237A8.27541S338C1307.349S175B6.430986S050B5.6S221A6.634646S149B7.82439S169B5.958065S392A7.785612S098B6.786667S139B6394.177S239C6.578082S307B5811.8S324B8.437956S088A7.103896S197B7.72381S310B8.92S213C2.989222S106B4.37S202B7.19403S376C5.230216S374C14298.7S036A6.301818S064A7.176296S025A5.902941S092B6.615267S157B5.98797S206C3.775S266A34.21992S113C7.757895S140A13322.49S253C9.621918S332C77.34615S172B4.631884S269A4.141026S030A17.76S086B793.1886S342C11.78537S152C7.153623S007A104.532S256C7.854962S141B8.482443S379A35.62105S067C2.948235S314B26.83051
供应商真实供货量如下图7所示：

图 7 供应商真实供货量
Fig.7 The actual supply of suppliers

2．模型的建立

(1)第i周企业的供货量

为了保证正常生产的需要，该企业要尽可能保持不少于满足两周生产需求的原材料库存量，为此该企业对供应商实际提供的原材料总是全部收购。每立方米产品消耗 A 类原材料 0.6 立方米或 B 类原材料 0.66 立方米或 C 类原材料 0.72 立方米。规定取A、B、C类材料每周对企业的供货量为w_i：

w_i=A_i/0.6+B_i/0.66+C_i/0.72

计算出能制造多少立方米的产品，w_1第一周企业的供货量需满足：

w_1≥28200*2

因为需要提前制定 24 周的原材料计划满足该企业每年按 48 周安排生产，计算从最大开始累加到28200*2立方米以上，累加式推导如下：

w_2+(w_1-28200)≥28200*2

同理可得：

w_i+w_(i-1)≥28200*3

(2)建立订购方案数学模型

采用一般线性规划不能解决选择供应商问题，需要用0-1规划[11]。设选择企业的集合 N，有n个供应商可供选择，为50家最重要的供应商建立数学模型[12]如下：

min|N|

另A_ij为A材料供应商j在第i周的供应量，同理：

A_(i=) ∑_(i∈N)▒A_ijB_(i=) ∑_(i∈N)▒B_ijC_(i=) ∑_(i∈N)▒C_ij

(3)转运商相关数据分析

在最优订购方案的基础上，对转运商损耗强度指标建立评价模型[13]，考虑损耗最少的转运方案[14]，分析运输损耗率方差、损耗率均值、有订单周数、订单占比量。

设损耗率为T_ik，运输损耗率均值¯(T_ik )，运输损耗率均值即总损耗率/周数：

¯(T_ik)=(∑▒T_ik)/n    

运输损耗率方差用来统计供货量数据时离散程度[15]的度量U_ik：

U_ik=(∑▒〖(T_ik-¯(T_ik))〗^2)/(n-1)

订单占比量E，对转运商订单数据进行分析，统计240周中转运商有订单的周数E_i，计算订单占比：

E=E_i/240

(4)各类材料周转运量模型建立

第k家转运商第i周A类原材料的供货量为u_ik (a)，B类原材料的供货量为u_ik (b)，C类原材料的供货量为u_ik ©，其中k∈K ， K表示转运商集合，r_ik表示第k家转运商第i周的转化率，那么第k家转运商第i周的被接收量为v_ik，各类材料周转运量模型 如下：

v_ik (a)=u_ik (a)(1-r_ik)    
        
v_ik (b)=u_ik (b)(1-r_ik)    
        
v_ik (c)=u_ik (c)(1-r_ik)

据此求解结果分析，转运商各原材料周接受量总和如下：

v_i (a)=∑_█(k∈K@r_jk≠0)▒〖v_ik (a)〗    
        
v_i (b)=∑_█(k∈K@r_jk≠0)▒〖v_ik (b)〗    
        
v_i (c)=∑_█(k∈K@r_jk≠0)▒〖v_ik (c)〗    

建立以选择供应商数量最少为目标的优化模型

min|N|=∑_(i=1)^n▒  x_i
s.t.{█(v_i (a)≥A_i@v_i(b)≥A_i@v_i(c)≥C_i)┤    

5 总结

5.1 模型的优点

对供货强度建立评价模型，以分析供应商保障企业生产重要性。本文对供货特征进行量化分析，计算供货量总量数统计，评估每周企业的订货量与供应商的供货量的值作为供货强度指标[17]。

整体上评价模型，利用加权平衡各系数比值，能直观得出企业充分利用订货量与攻击力信息进行分析，有效吸收定性分析的结果，发挥了定量分析[18]的优势，评价结果具有很强的条理性与科学性，是保障企业生产的重要数学模型。

在处理企业应至少选择多少家供应商供应原材料才可能满足生产的需求问题求解中，建立性0 - 1规划模型确定供应商数，并将遗传算法应用[19]于订购方案与转运方案的寻优过程中，增加了模型的准确性，符合方案的实际情况。
在制定新的订购方案及转运方案并分析方案的实施效果中，建立了迭代模型，增加了新方案的精准性与模型的严谨性。

5.2 模型的缺点

在对问题二的求解过程中，在预测结果选择每周损耗率最少的转运商，加上将转运商至寻优模型中，增加了数据变量的维度，降低全局最优解概率以及模型的普适性。

在制定新的订购方案及转运方案并分析方案[20]的实施效果中，数据的统计和处理较少，对数据的真实性较低，只获取单个数据，模型很建立的精确度较差。

在去噪声处理中，本文并未采用多种去噪声方法来进行效果比对，缺乏对比性实验，对中值噪声模型检验无法形成更精准的有效性。

参考文献

[1] 李丽. 模糊随机供需环境下的供应商管理库存(VMI)的订货量模型研究[D]. 同济大学, 2010.
[2] 姚建明, 蒲云, 周国华,等. 多品种供应的多供应商选择模型及分解算法[J]. 西南交通大学学报, 2005, 040(004):519-524.
[3] 杨昆, 徐静, 张彦斌. 基因选择的0-1规划模型和算法[J]. 计算机工程与应用, 2010, 46(020):184-187.
[4] 王珏. 带有原材料订购的供货商与销售商联合生产库存模型[J]. 安徽建筑工业学院学报:自然科学版, 2010, 18(5):90-90.
[5] 陈俊霖. 基于库存和备用供应商应对供货风险的策略研究[D].清华大学,2012.
[6] 于萍, 季建华, 顾巧论. MC条件下两阶段供应商生产计划优化模型研究[J]. 重庆交通大学学报（自然科学版）, 2008, 27(4):661-664.
[7] 王小璞, 张朋, 李兴东,等. 一种块迭代的快速代数重建算法[J]. Ct理论与应用研究, 2004, 9(z1):10-12.
[8] 安健期, 张绍文. 供链库存管理中最优化模型研究综述[J]. 物流工程与管理, 2010, 32(9):98-99.
[9] 黄亮亮, 王勇. The Average Investment Portfolio Risk Analysis of Variance%投资组合风险的均值方差分析[J]. 上海电力学院学报, 2012, 028(003):287-290,297.
[10] 邓雪, 李家铭, 曾浩健,等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7):93-100.
[11] 吴桂芳. 物流配送中心选址优化模型及算法研究[D]. 武汉理工大学.
[12] 沈晓芳. 基于遗传算法的函数寻优算法[J]. 课程教育研究(7):1.
[13] 万国华,孙磊.批量运输的二层供应链系统的生产和订购计划:模型与算法[J].系统管理学报,2012,21(06):729-735.
[14]张立.钢管订购与运输的优化模型[J].常熟理工学院学报,2006(04):37-40.DOI:10.16101/j.cnki.cn32-1749/z.2006.04.008.
[15] 王庆泉,武和雷,方梦飞.基于遗传模拟退火算法的钢管订购和运输优化问题求解[J].南昌大学学报(工科版),2007(01):94-98.
[16] 许先云.钢管订购和运输数学模型的研究[J].湖南轻工业高等专科学校学报,2003(04):1-3.
[17] 陆维新,林皓,陈晓东,周杰.订购和运输钢管的最优方案[J].数学的实践与认识,2001(01):74-78.
[18] 王娜. 基于分散化收益的供应商数量选择和订货量分配策略研究[D].东北大学,2008.
[19] 徐艳飞. 不确定性环境下最优供应商数量和订单分配问题研究[D]. 燕山大学.
[20] 潘伟. 供应链环境中订单分配及订购批量决策研究[D]. 华中科技大学, 2009.