自从扩散模型发布以来,GAN的关注度和论文是越来越少了,但是它们里面的一些思路还是值得我们了解和学习。所以本文我们来使用Pytorch 来实现SN-GAN
谱归一化生成对抗网络是一种生成对抗网络,它使用谱归一化技术来稳定鉴别器的训练。谱归一化是一种权值归一化技术,它约束了鉴别器中每一层的谱范数。这有助于防止鉴别器变得过于强大,从而导致不稳定和糟糕的结果。
SN-GAN由Miyato等人(2018)在论文“生成对抗网络的谱归一化”中提出,作者证明了sn - gan在各种图像生成任务上比其他gan具有更好的性能。
SN-GAN的训练方式与其他gan相同。生成器网络学习生成与真实图像无法区分的图像,而鉴别器网络学习区分真实图像和生成图像。这两个网络以竞争的方式进行训练,它们最终达到一个点,即生成器能够产生逼真的图像,从而欺骗鉴别器。
以下是SN-GAN相对于其他gan的优势总结:
- 更稳定,更容易训练
- 可以生成更高质量的图像
- 更通用,可以用来生成更广泛的内容。
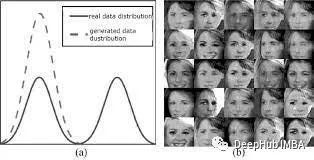
模式崩溃
模式崩溃是生成对抗网络(GANs)训练中常见的问题。当GAN的生成器网络无法产生多样化的输出,而是陷入特定的模式时,就会发生模式崩溃。这会导致生成的输出出现重复,缺乏多样性和细节,有时甚至与训练数据完全无关。
GAN中发生模式崩溃有几个原因。一个原因是生成器网络可能对训练数据过拟合。如果训练数据不够多样化,或者生成器网络太复杂,就会发生这种情况。另一个原因是生成器网络可能陷入损失函数的局部最小值。如果学习率太高,或者损失函数定义不明确,就会发生这种情况。
以前有许多技术可以用来防止模式崩溃。比如使用更多样化的训练数据集。或者使用正则化技术,例如dropout或批处理归一化,使用合适的学习率和损失函数也很重要。
Wassersteian损失
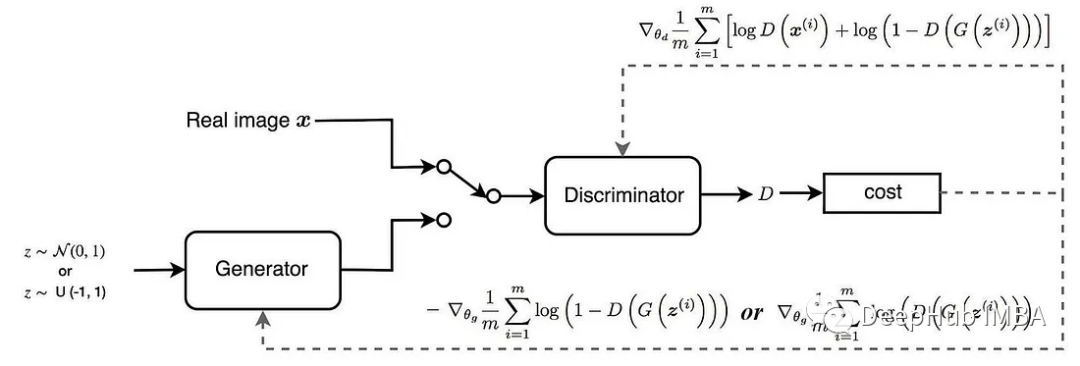
Wasserstein损失,也称为Earth Mover’s Distance(EMD)或Wasserstein GAN (WGAN)损失,是一种用于生成对抗网络(GAN)的损失函数。引入它是为了解决与传统GAN损失函数相关的一些问题,例如Jensen-Shannon散度和Kullback-Leibler散度。
Wasserstein损失测量真实数据和生成数据的概率分布之间的差异,同时确保它具有一定的数学性质。他的思想是最小化这两个分布之间的Wassersteian距离(也称为地球移动者距离)。Wasserstein距离可以被认为是将一个分布转换为另一个分布所需的最小“成本”,其中“成本”被定义为将概率质量从一个位置移动到另一个位置所需的“工作量”。

Wasserstein损失的数学定义如下:
对于生成器G和鉴别器D, Wasserstein损失(Wasserstein距离)可以表示为:
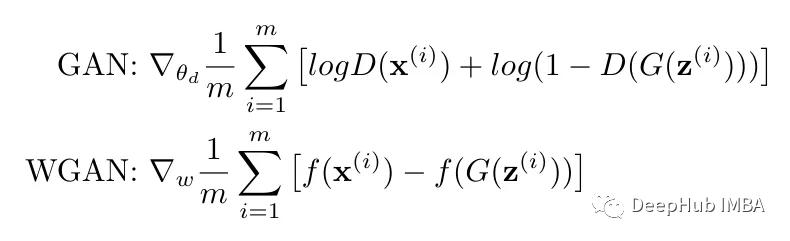
Jensen-Shannon散度(JSD): Jensen-Shannon散度是一种对称度量,用于量化两个概率分布之间的差异
对于概率分布P和Q, JSD定义如下:
JSD(P∥Q)=1/2(KL(P∥M)+KL(Q∥M))
M为平均分布,KL为Kullback-Leibler散度,P∥Q为分布P与分布Q之间的JSD。
JSD总是非负的,在0和1之间有界,并且对称(JSD(P|Q) = JSD(Q|P))。它可以被解释为KL散度的“平滑”版本。
Kullback-Leibler散度(KL散度):Kullback-Leibler散度,通常被称为KL散度或相对熵,通过量化“额外信息”来测量两个概率分布之间的差异,这些“额外信息”需要使用另一个分布作为参考来编码一个分布。
对于两个概率分布P和Q,从Q到P的KL散度定义为:KL(P∥Q)=∑x P(x)log(Q(x)/P(x))。KL散度是非负非对称的,即KL(P∥Q)≠KL(Q∥P)。当且仅当P和Q相等时它为零。KL散度是无界的,可以用来衡量分布之间的不相似性。

1-Lipschitz Contiunity
1- lipschitz函数是斜率的绝对值以1为界的函数。这意味着对于任意两个输入x和y,函数输出之间的差不超过输入之间的差。
数学上函数f是1-Lipschitz,如果对于f定义域内的所有x和y,以下不等式成立:
|f(x) — f(y)| <= |x — y|
在生成对抗网络(GANs)中强制Lipschitz连续性是一种用于稳定训练和防止与传统GANs相关的一些问题的技术,例如模式崩溃和训练不稳定。在GAN中实现Lipschitz连续性的主要方法是通过使用Lipschitz约束或正则化,一种常用的方法是Wasserstein GAN (WGAN)。
在标准gan中,鉴别器(也称为WGAN中的批评家)被训练来区分真实和虚假数据。为了加强Lipschitz连续性,WGAN增加了一个约束,即鉴别器函数应该是Lipschitz连续的,这意味着函数的梯度不应该增长得太大。在数学上,它被限制为:
∥∣D(x)−D(y)∣≤K⋅∥x−y∥
其中D(x)是评论家对数据点x的输出,D(y)是y的输出,K是Lipschitz 常数。
WGAN的权重裁剪:在原始的WGAN中,通过在每个训练步骤后将鉴别器网络的权重裁剪到一个小范围(例如,[-0.01,0.01])来强制执行该约束。权重裁剪确保了鉴别器的梯度保持在一定范围内,并加强了利普希茨连续性。
WGAN的梯度惩罚: WGAN的一种变体,称为WGAN-GP,它使用梯度惩罚而不是权值裁剪来强制Lipschitz约束。WGAN-GP基于鉴别器的输出相对于真实和虚假数据之间的随机点的梯度,在损失函数中添加了一个惩罚项。这种惩罚鼓励了Lipschitz约束,而不需要权重裁剪。
谱范数
从符号上看矩阵𝑊的谱范数通常表示为:对于神经网络𝑊矩阵表示网络层中的一个权重矩阵。矩阵的谱范数是矩阵的最大奇异值,可以通过奇异值分解(SVD)得到。
奇异值分解是特征分解的推广,用于将矩阵分解为
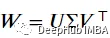
其中𝑈,q为正交矩阵,Σ为其对角线上的奇异值矩阵。注意Σ不一定是正方形的。
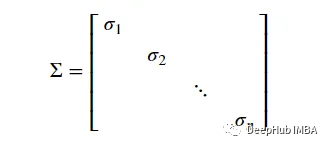
其中𝜎1和𝑛分别为最大奇异值和最小奇异值。更大的值对应于一个矩阵可以应用于另一个向量的更大的拉伸量。依此表示,𝜎(𝑊)=𝜎1.
SVD在谱归一化中的应用
为了对权矩阵进行频谱归一化,将矩阵中的每个值除以它的频谱范数。谱归一化矩阵可以表示为
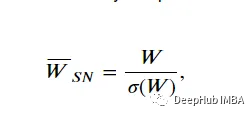
计算𝑊is的SVD非常昂贵,所以SN-GAN论文的作者做了一些简化。它们通过幂次迭代来近似左、右奇异向量𝑢和𝑣,分别为:𝑊)≈𝑢
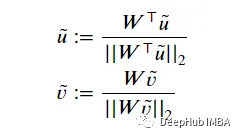
代码实现
现在我们开始使用Pytorch实现
import torch
from torch import nn
from tqdm.auto import tqdm
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import make_grid
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
torch.manual_seed(0)
def show_tensor_images(image_tensor, num_images=25, size=(1, 28, 28)):
image_tensor = (image_tensor + 1) / 2
image_unflat = image_tensor.detach().cpu()
image_grid = make_grid(image_unflat[:num_images], nrow=5)
plt.imshow(image_grid.permute(1, 2, 0).squeeze())
plt.show()
生成器:
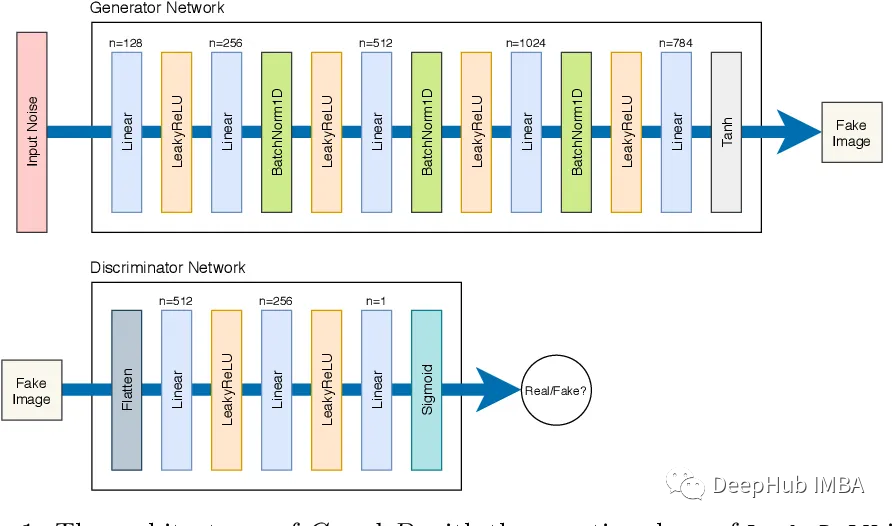
class Generator(nn.Module):
def __init__(self,z_dim=10,im_chan = 1,hidden_dim = 64):
super(Generatoe,self).__init__()
self.gen = nn.Sequential(
self.make_gen_block(z_dim,hidden_dim * 4),
self.make_gen_block(hidden_dim*4,hidden_dim * 2,kernel_size = 4,stride =1),
self.make_gen_block(hidden_dim * 2,hidden_dim),
self.make_gen_block(hidden_dim,im_chan,kernel_size=4,final_layer = True),
)
def make_gen_block(self,input_channels,output_channels,kernel_size=3,stride=2,final_layer = False):
if not final_layer :
return nn.Sequential(nn.ConvTranspose2D(input_layer,output_layer,kernel_size,stride),
nn.BatchNorm2d(output_channels),
nn.ReLU(inplace = True),
)
else:
return nn.Sequential(nn.ConvTranspose2D(input_layer,output_layer,kernel_size,stride),
nn.Tanh(),)
def unsqueeze_noise():
return noise.view(len(noise), self.z_dim, 1, 1)
def forward(self,noise):
x = self.unsqueeze_noise(noise)
return self.gen(x)
def get_noise(n_samples, z_dim, device='cpu'):
return torch.randn(n_samples, z_dim, device=device)
鉴频器
对于鉴别器,我们可以使用spectral_norm对每个Conv2D 进行处理。除了𝑊之外,还引入了𝑢、𝑣、和其他的参数,这样在运行时就可以计算出𝑊𝑆的二进制二进制运算符:𝑢、y、y、y、y
因为Pytorch还提供 nn.utils. spectral_norm,nn.utils. remove_spectral_norm函数,所以我们操作起来很方便。
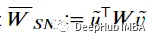
我们只在推理期间将nn.utils. remove_spectral_norm应用于卷积层,以提高运行速度。
值得注意的是,谱范数并不能消除对批范数的需要。谱范数影响每一层的权重,批范数影响每一层的激活度。
class Discriminator(nn.Module):
def __init__(self, im_chan=1, hidden_dim=16):
super(Discriminator, self).__init__()
self.disc = nn.Sequential(
self.make_disc_block(im_chan, hidden_dim),
self.make_disc_block(hidden_dim, hidden_dim * 2),
self.make_disc_block(hidden_dim * 2, 1, final_layer=True),
)
def make_disc_block(self, input_channels, output_channels, kernel_size=4, stride=2, final_layer=False):
if not final_layer:
return nn.Sequential(
nn.utils.spectral_norm(nn.Conv2d(input_channels, output_channels, kernel_size, stride)),
nn.BatchNorm2d(output_channels),
nn.LeakyReLU(0.2, inplace=True),
)
else:
return nn.Sequential(
nn.utils.spectral_norm(nn.Conv2d(input_channels, output_channels, kernel_size, stride)),
)
def forward(self, image):
disc_pred = self.disc(image)
return disc_pred.view(len(disc_pred), -1)
训练
我们这里使用MNIST数据集,bcewithlogitsloss()函数计算logit和目标标签之间的二进制交叉熵损失。二值交叉熵损失是对两个分布差异程度的度量。在二元分类中,这两种分布分别是逻辑的分布和目标标签的分布。
criterion = nn.BCEWithLogitsLoss()
n_epochs = 50
z_dim = 64
display_step = 500
batch_size = 128
# A learning rate of 0.0002 works well on DCGAN
lr = 0.0002
beta_1 = 0.5
beta_2 = 0.999
device = 'cuda'
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
dataloader = DataLoader(
MNIST(".", download=True, transform=transform),
batch_size=batch_size,
shuffle=True)
创建生成器和鉴别器
gen = Generator(z_dim).to(device)
gen_opt = torch.optim.Adam(gen.parameters(), lr=lr, betas=(beta_1, beta_2))
disc = Discriminator().to(device)
disc_opt = torch.optim.Adam(disc.parameters(), lr=lr, betas=(beta_1, beta_2))
# initialize the weights to the normal distribution
# with mean 0 and standard deviation 0.02
def weights_init(m):
if isinstance(m, nn.Conv2d) or isinstance(m, nn.ConvTranspose2d):
torch.nn.init.normal_(m.weight, 0.0, 0.02)
if isinstance(m, nn.BatchNorm2d):
torch.nn.init.normal_(m.weight, 0.0, 0.02)
torch.nn.init.constant_(m.bias, 0)
gen = gen.apply(weights_init)
disc = disc.apply(weights_init)
下面是训练步骤
cur_step = 0
mean_generator_loss = 0
mean_discriminator_loss = 0
for epoch in range(n_epochs):
# Dataloader returns the batches
for real, _ in tqdm(dataloader):
cur_batch_size = len(real)
real = real.to(device)
## Update Discriminator ##
disc_opt.zero_grad()
fake_noise = get_noise(cur_batch_size, z_dim, device=device)
fake = gen(fake_noise)
disc_fake_pred = disc(fake.detach())
disc_fake_loss = criterion(disc_fake_pred, torch.zeros_like(disc_fake_pred))
disc_real_pred = disc(real)
disc_real_loss = criterion(disc_real_pred, torch.ones_like(disc_real_pred))
disc_loss = (disc_fake_loss + disc_real_loss) / 2
# Keep track of the average discriminator loss
mean_discriminator_loss += disc_loss.item() / display_step
# Update gradients
disc_loss.backward(retain_graph=True)
# Update optimizer
disc_opt.step()
## Update Generator ##
gen_opt.zero_grad()
fake_noise_2 = get_noise(cur_batch_size, z_dim, device=device)
fake_2 = gen(fake_noise_2)
disc_fake_pred = disc(fake_2)
gen_loss = criterion(disc_fake_pred, torch.ones_like(disc_fake_pred))
gen_loss.backward()
gen_opt.step()
# Keep track of the average generator loss
mean_generator_loss += gen_loss.item() / display_step
## Visualization code ##
if cur_step % display_step == 0 and cur_step > 0:
print(f"Step {cur_step}: Generator loss: {mean_generator_loss}, discriminator loss: {mean_discriminator_loss}")
show_tensor_images(fake)
show_tensor_images(real)
mean_generator_loss = 0
mean_discriminator_loss = 0
cur_step += 1
训练结果如下:

总结
本文我们介绍了SN-GAN的原理和简单的代码实现,SN-GAN已经被广泛应用于图像生成任务,包括图像合成、风格迁移和超分辨率等领域。它在改善生成模型的性能和稳定性方面取得了显著的成果,所以学习他的代码对我们理解会更有帮助。
作者:DhanushKumar