【C语言 - 数据结构】树、二叉树（下篇）

假设，我手头有 20张100元的和2000张1元的奖券，同时洒向了空中，大家比赛看谁最终捡的最多。如果是你，你会怎么做?

相信所有同学都会说，一定先捡 100 元的。道理非常简单，因为捡一张100元等1元的捡100 张，效率好得不是一点点。所以可以得到这样的结论，同样是捡奖券，在有限时间内，要达到最高效率，次序非常重要。对于二叉树的遍历来讲，次序同样显得很重要。

                               超乎一切之上的一件事,就是保持青春朝气。——莎士比亚 

文章目录

• 一、二叉树的遍历原理
• 二、二叉树的前序、中序、后序、层序遍历
• 三、二叉树的拓展：判断树的高度、每层的结点个数等
• 四、二叉树oj题
• 总结

提示：以下是本篇文章正文内容，下面案例可供参考

一、二叉树的遍历原理

1.1原理：

二叉树的遍历（traveing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中所有的结点，使每个结点都被访问一次，且仅被访问一次。

    这里有两个关键词：访问和次序。

1.2.1访问

    访问其实是要根据实际的需要来确定具体做什么，比如对每个结点进行相关计算，输出打印等，它算作是一个抽象操作。在这里我们可以简单地假定就是输出结点的数据信息。

1.2.2次序

    二叉树的遍历次序不同于线性结构，最多也就是从头至尾、循环、双向等简单的遍历方式。树的结点之间不存在唯一的前驱和后继关系，在访问一个结点后，下一个被访问的结点面临着不同的选择就像你人生的道路上，高考填志愿要面临哪个城市、哪所大学、具体专业等选择，由选择方式的不同，遍历的次序就完全不同了。

二、二叉树的前序、中序、后序遍历

2.1二叉树遍历的几种方式

    二叉树的遍历方式可以很多，如果我们限制了从左到右的习惯方式，那么主要就分为四种：

前序遍历、中序遍历、后序遍历、层次遍历。

这四种遍历方式的基本顺序和在数组中存储的形式如下图所示：

2.2前序遍历

    规则是若 叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。如图遍历的顺序为: ABDGHCEIF

步骤：1、先造一颗树

造树：

#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
       struct BinaryTreeNode* left;
       struct BinaryTreeNode* right;
       BTDataType data;
}BTNode;
malloc一块空间
BTNode* BuyBTNode(BTDataType x)
{
       BTNode* node = (BTNode*)malloc(sizeof(BTNode));
       if (node == NULL)
       {
              printf("malloc fail\n");
              exit(-1);
       }
       node->data = x;
       node->left = node->right = NULL;
       return node;
}
紧接着实现链接
BTNode* CreatBinaryTree()
{
       BTNode* node1 = BuyBTNode(1);
       BTNode* node2 = BuyBTNode(2);
       BTNode* node3 = BuyBTNode(3);
       BTNode* node4 = BuyBTNode(4);
       BTNode* node5 = BuyBTNode(5);
       BTNode* node6 = BuyBTNode(6);
       node1->left = node2;
       node1->right = node4;
       node2->left = node3;
       node4->left = node5;
       node4->right = node6;
       return node1;
}

2、写前序遍历和main函数

void PrevOrder(BTNode* root)//前序遍历
{
       if (root == NULL)//如果根是空就return
       {
              printf("NULL ");
              return;
       }
       printf("%d ", root->data);
       PrevOrder(root->left);//左子树
       PrevOrder(root->right);//右子树
}
int main()
{
       BTNode* tree = CreatBinaryTree();
       PrevOrder(tree);
       return 0;
}

程序运行结果 ：（对照1、2、3、4、5、6）上图

2.3中序遍历

    规则是若树为空，则空操作返回，否则从根结点开始(注意并不是先访问根结 点) ，中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树 如图所示， 遍历的顺序为GDHBAELCF.

void InOrder(BTNode* root)//中序遍历
{
       if (root == NULL)//如果根是空就return
       {
              printf("NULL ");
              return;
       }
       InOrder(root->left);//先左子树
       printf("%d ", root->data);
       InOrder(root->right);//再右子树
}
int main()
{
       BTNode* tree = CreatBinaryTree();
       InOrder(tree);
       return 0;
}

程序运行结果

2.4后序遍历

    规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点 如图所示 遍历的顺序为 GHDBIEFCA。

void BackOrder(BTNode* root)
{
       if (root == NULL)//如果根是空就return
       {
              printf("NULL ");
              return;
       }
       BackOrder(root->left);
       BackOrder(root->right);
       printf("%d ", root->data);
}
int main()
{
       BTNode* tree = CreatBinaryTree();
       BackOrder(tree);
       
       return 0;
}

程序运行结果：

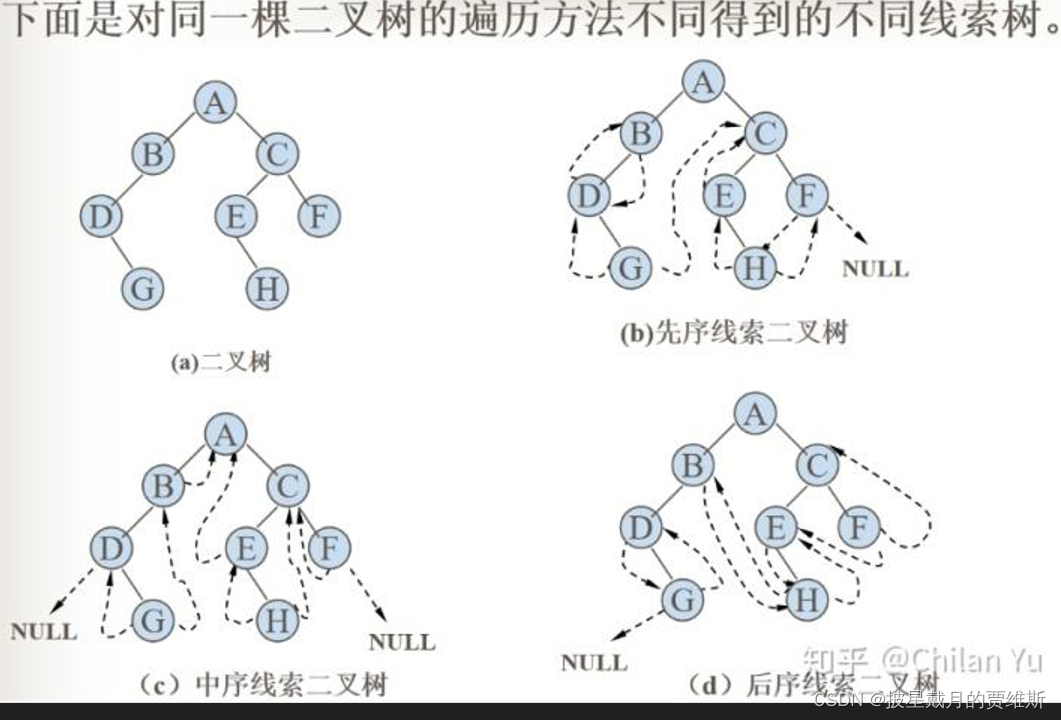
二叉树的遍历的几种路径 （小结）：网上找的图

2.5层序遍历

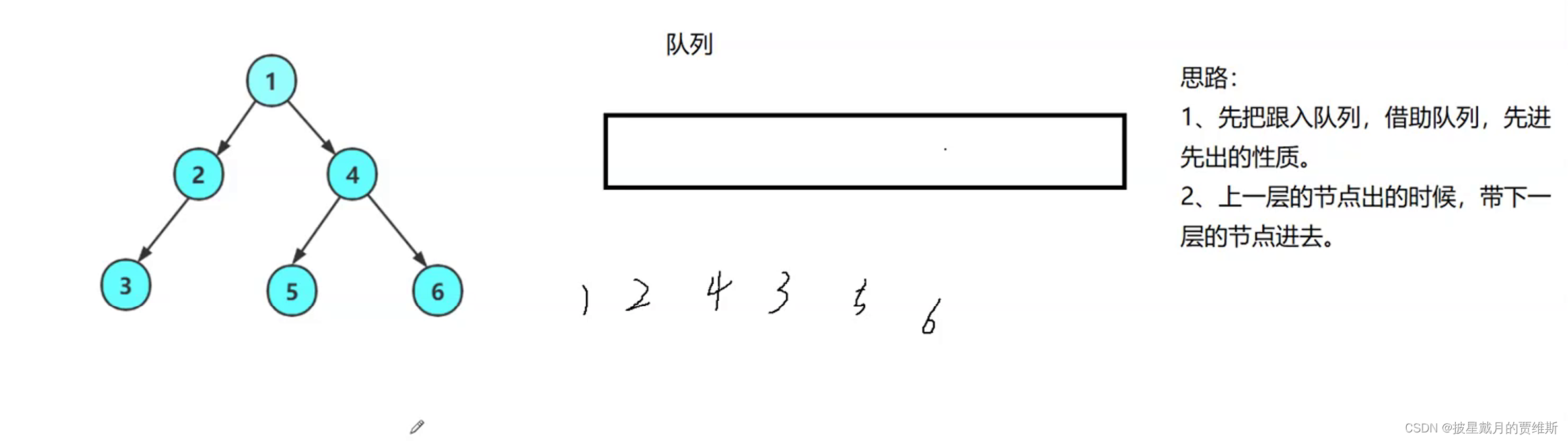
    层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在 层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

层序遍历与之前的三种遍历情况有所不同，层序遍历的实现依赖于队列，会比较麻烦一些。

//层序遍历
void LevelOrder(BTNode* root)
{
       Queue q;
       QueueInit(&q);
       if (root)
       {
              QueuePush(&q, root);//先插入根节点
       }
       while (QueueEmpty(&q))
       {
              BTNode* front = QueueFront(&q);
              QueuePop(&q);//把队列里根节点的指针拿出来，但是指针指向的节点的值没有被销毁；
              printf("%d ", front->data);
              if (front->left)
              {
                      QueuePush(&q, front->left);
              }
              if (front->right)
              {
                      QueuePush(&q, front->right);
              }
              printf("\n");
       }
       QueueDestry(&q);
}

三、二叉树的拓展

3.1计算树的结点的个数

low版（代码比较挫）但是容易理解

int count = 0;
void BTreeSize(BTNode* root)
{
       if (root == NULL)
              return;
       ++count;
       BTreeSize(root->left);
       BTreeSize(root->right);
       //后序
}

注意：

这里为什么不用static静态变量。

因为静态变量在静态区，是整个程序结束后才销毁，而且局部静态变量不能置零

所以如果再计算下一个树的结点就会和上一个树累加。

static只初始化一次，所以要么就是全局静态变量。

具体的调用方法：//更好的计数方法，既不使用全局，也不使用静态变量-

//思想遍历加计数（传地址调用）指针

void BTreeSize(BTNode* root, int* pCount)
{
       if (root == NULL)
              return;
       ++(*pCount);//把一个变量的地址传过去
       BTreeSize(root->left, pCount);
       BTreeSize(root->right, pCount);
       //后序
}

3.2计算树的叶子结点的个数

思路：叶子结点的左右结点都为空，递归+分治思想

因此：代码如下

int BTreeLaafSize(BTNode* root)
{
       if (root == NULL)
              return 0;
       if (root->left == NULL && root->right == NULL)
              return 1;
       return BTreeLaafSize(root->left) + BTreeLaafSize(root->right);
       
}

3.3怎么求第k层节点的个数？

核心思路：递归返回第k-1层左右结点相加的值

int BTreekLeafSize(BTNode* root, int k)
{
       assert(k >= 1);
       if (root == NULL) return 0;
       if (k == 1) return 1;
       return BTreekLeafSize(root->left, k - 1) + BTreekLeafSize(root->right, k - 1);//返回左结点和右结点的上一层
}

3.4求一棵树的高度

思想：比较左右子树的高度，并且返回高度大的加一（原因：加根结点）

int BTreeDepth(BTNode* root)
{
       if (root == NULL)
              return 0;
       int leftDepth = BTreeDepth(root->left);
       int rightDepth = BTreeDepth(root->right);
       return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

3.5二叉树查找值为x的结点

思路：用前序遍历去递归搜索，先搜左子树，如果左子树没有，就返回一个NULL到根结点，然后根结点再递归搜索右树，如果右树有就返回那个点的值。

BTNode* BTreeFind(BTNode* root, BTDataType x)
{
       if (root == NULL)
              return NULL;
       if (root->data == x)
              return root;
       //用前序遍历的思想
       BTNode* ret1 = BTreeFind(root->left, x);//先去递归左树
       if (ret1)//如果左边返回的不是NULL
       {
              return ret1;
       }
       BTNode* ret2 = BTreeFind(root->right, x);
       if (ret2)
       {
              return ret2;
       }
       return NULL;
}

3.6判断一棵树是不是完全二叉树

思路：就是把空也当作二叉树的节点放进去，然后运用层序遍历，

如果在遍历的中间过程中遇到空就说明不是完全二叉树。

队列不能直接像数组一样遍历

//判断一棵树是不是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
       Queue q;
       QueueInit(&q);
       if (root)
       {
              QueuePush(&q, root);//先插入根节点
       }
       while (!QueueEmpty(&q))
       {
              BTNode* front = QueueFront(&q);//会等于队头第一个数据的值
              QueuePop(&q);
              if (front == NULL)
              {
                      break;
              }
              QueuePush(&q, front->left);
              QueuePush(&q, front->right);
       }
       while (!QueueEmpty(&q))
       {
              BTNode* front = QueueFront(&q);//会等于队头第一个数据的值
              QueuePop(&q);
              if (front)//如果出到非空，那么就不是完全二叉树
              {
                      return false;
              }
       
       }
       return true;
}

四、二叉树oj题

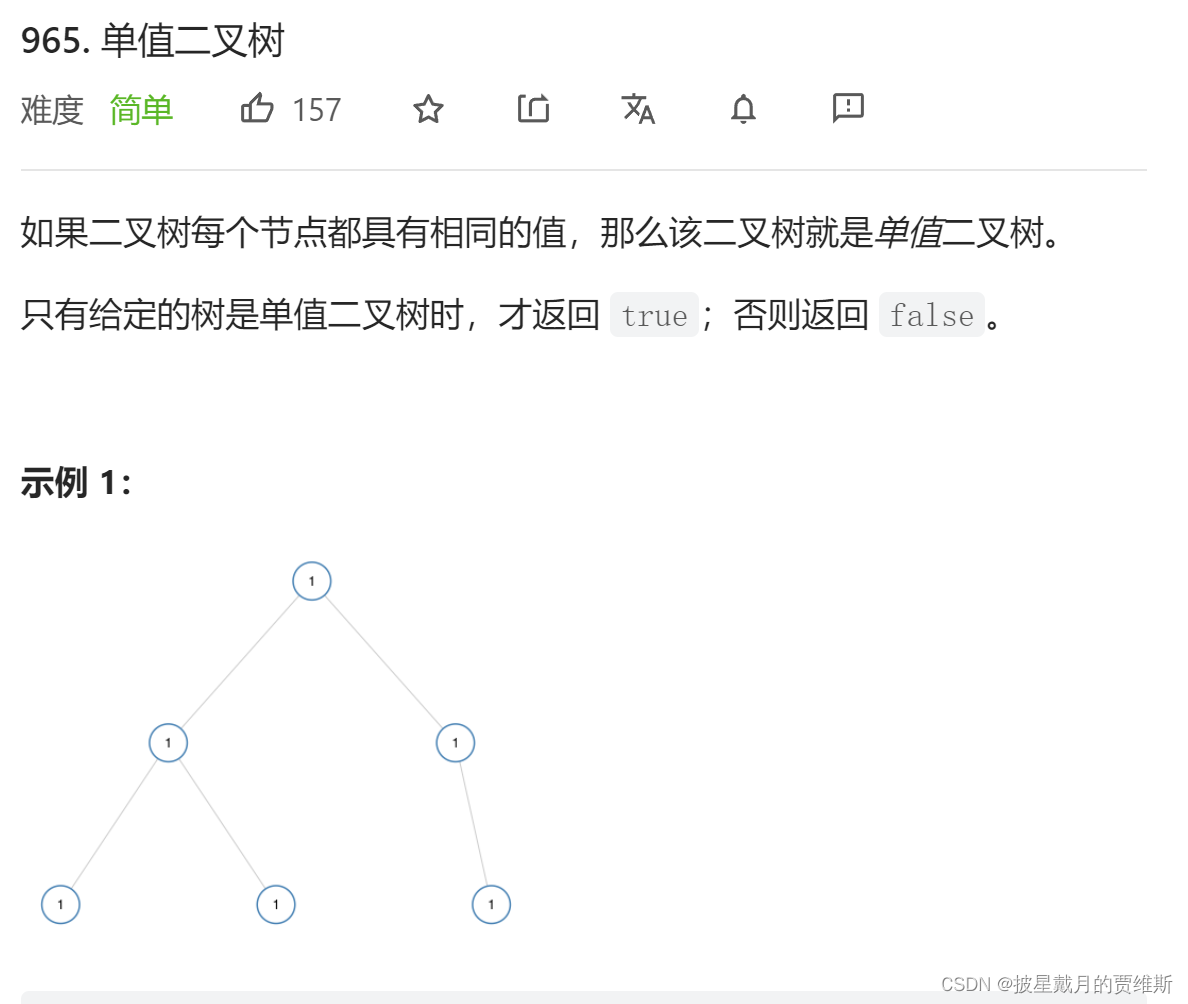
1、965. 单值二叉树 - 力扣（LeetCode）

bool isUnivalTree(struct TreeNode* root)
{
    if(root == NULL) return true;
    if(root->left && root->left->val != root->val)//如果左结点不为空，且左树结点的值不等于根的值，返回false
 
         return false;
    if(root->right && root->right->val != root->val)//如果右结点不为空，且右树结点的值不等于根的值，返回false
        return false;
    return isUnivalTree(root->left) && isUnivalTree(root->right);//递归判断
}

2、100. 相同的树 - 力扣（LeetCode）

思路：先判断两棵树是不是都是空树，再判断如果一个为空一个不为空，最后递归

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    //判断两个树的根是不是都为空
    if(p == NULL && q == NULL)
        return true;
    //判断两个树的其中一颗树的结点为空时，另一个不为空
    if(p == NULL || q == NULL)
        return false;
    //判断两个树的根节点是否是同值
    if(p->val != q->val)
        return false;
        //递归判断
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
注意：这里的判断不能写成p->left->val != q->left->val
会报错

3、101. 对称二叉树 - 力扣（LeetCode）

思路：写一个辅助函数，舍弃根结点，判断左边这个树是否与右边这个树对称

bool isSymmetricTree(struct TreeNode* p, struct TreeNode* q)
{
    //如果root的左和右节点都为空
    if(p == NULL && q == NULL) 
    return true;
    //如果一个为空一个不为空
    if(p == NULL || q == NULL) 
    return false;

    return p->val == q->val 
    && isSymmetricTree(p->left, q->right)
    && isSymmetricTree(p->right, q->left);

}
bool isSymmetric(struct TreeNode* root)
{
    if(root == NULL) 
    return true;

    return isSymmetricTree(root->left, root->right);
}

4、144. 二叉树的前序遍历 - 力扣（LeetCode）

题目意思解释：Note: The returned array must be malloced, assume caller calls free().

这句话的意思是数组要malloc， 然后caller系统会帮你free掉

int* returnSize的意思是返回结点的个数

代码如下所示：

int TreeSize(struct TreeNode* root)//计算树的结点个数，方便malloc空间
{
    return root == NULL ? 0 : TreeSize(root->left) + 
    TreeSize(root->right) + 1;
}
//定义一个子函数去完成前序遍历
void _preorder(struct TreeNode* root, int* a,int *pi)
{
    if(root == NULL)
      return;
    a[(*pi) ++] = root->val;//控一下优先级*的优先级低于++，所以要加（）
    _preorder(root->left, a, pi);
    _preorder(root->right, a, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)//int*returnSize是输出型参数
{
    int size = TreeSize(root);
    //不考虑动态扩容
    int* a = malloc(sizeof(int)*size);
    int i = 0;
    *returnSize = size;
    _preorder(root, a, &i);
    return a;
}

因为之后的二叉树中序以及后序遍历思路差不多，所以如果读者有兴趣可以根据这个思路去做。

5、572. 另一棵树的子树 - 力扣（LeetCode）

思路：左边树中每一个子树都比较isSameTree

遍历左边的每个节点，做子树的根，跟右边的子树都比较一下isSameTree

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    //两棵树的根都为空
    if (p == NULL && q == NULL)
        return true;
    //只有一颗树为空 此时已经有同位置的节点不相等
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
    return false;
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root == NULL)
        return;
    if(isSameTree(root, subRoot))
    {
        return true;
    }
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

6.二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

先序遍历字符串构造的二叉树（前序）

递归、分治的思想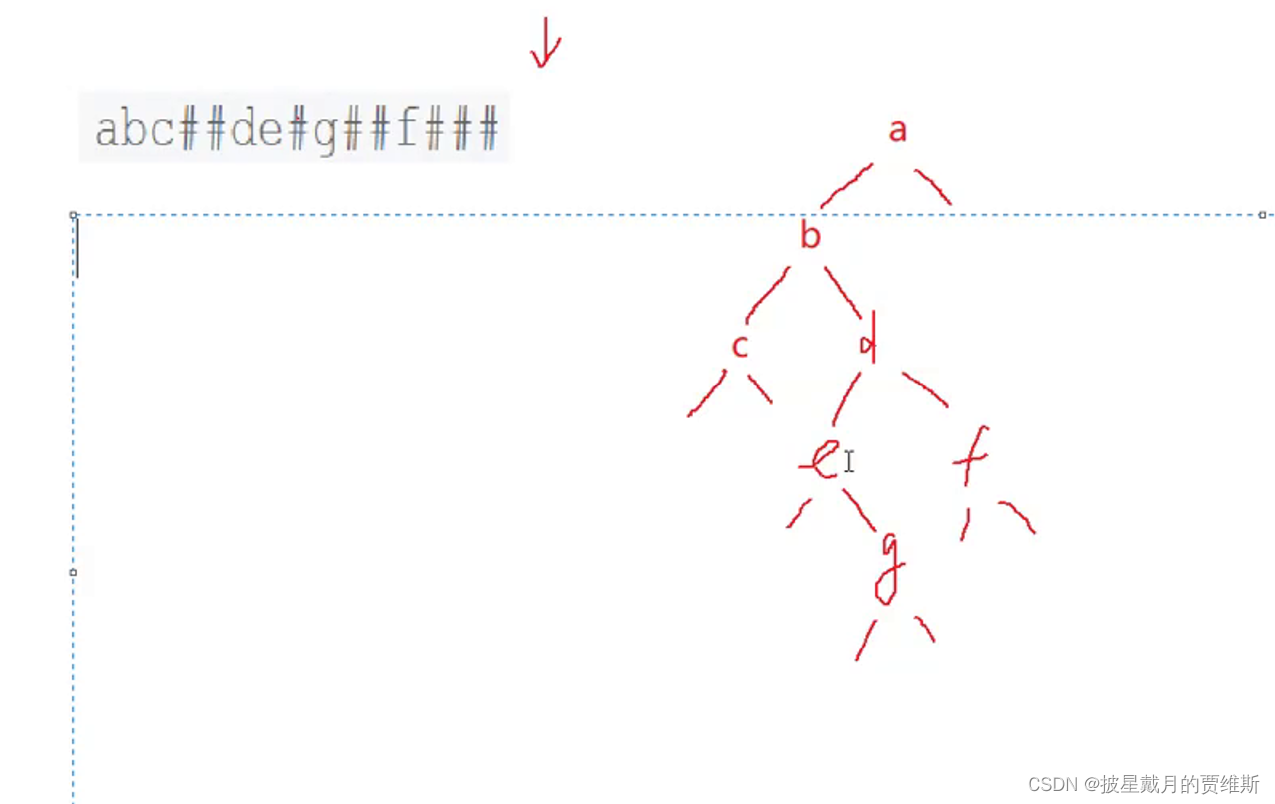

#include<stdio.h>
#include<string.h>
//构造结构体
typedef struct BinaryTreeNode
{
    char data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;
//造树
BTNode* CreatTree(char* a, int* pi)
{
    if(a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    
    root->data = a[(*pi)++];
    root->left = CreatTree(a, pi);
    root->right = CreatTree(a, pi);
    return root;
}
void InOrder(BTNode* root)
{
    if(root == NULL)//这里root直接等于NULL判断便可，不需要‘#
    {
        return;
    }
    InOrder(root->left);
    printf("%c ", root->data);
    InOrder(root->right);
}
//main函数部分
int main ()
{
    char a[101];
    scanf("%s", a);
    int i = 0;
    BTNode* tree = CreatTree(a, &i);
    InOrder(tree);
    return 0;
}

总结

     本文写了近8000字大致总结了二叉树的遍历算法，从二叉树的遍历原理、以及四个常见的二叉树的遍历算法：前、中、后、层序遍历算法，以及二叉树衍生出的6个拓展问题，6道二叉树oj题四个点展开，争取把二叉树的遍历讲透，希望大家读后能够有所收获。