人工智能——神经网络算法入门

概述

神经网络算法是一种模拟人脑神经元网络结构的计算方法，核心思想是通过大量简单的基本计算单元（即神经元）相互连接来处理复杂的模式识别、优化等问题。

典型的神经网络算法包括输入层、隐藏层和输出层。输入层负责接收外部输入的数据，隐藏层通过一系列复杂的计算将输入转化为有意义的特征，最后输出层将特征转化为具体的输出结果。

神经网络算法的优势在于其具有良好的自适应性、自组织和自学习能力，可以自动地根据输入数据进行学习和优化，从而在很大程度上解决了复杂的模式识别、优化等问题。同时，神经网络算法还具有很好的容错性和鲁棒性，可以有效地处理不完全或错误的数据。

神经元学习理论

单一神经元

单一神经元学习理论主要是根据神经元之间的连接强度（即权重）进行调整，以适应环境变化

单一神经元可以对多个输入信号，分别乘以权重并进行相加，并施加偏置量。再用激活函数进行处理。 权重可以调整每个输入的影响力。偏置可以调整进入激活函数的值，可以表示神经元灵敏度的值。

激活函数和损失函数

激活函数的作用：

1. 控制输入对输出的激活作用：决定一个神经元是否应该被激活或抑制。通过将神经元的净输入（即输入信号与权重的乘积之和）映射到输出端，实现对输入信号的非线性变换。
2. 对输入、输出进行函数转换：激活函数可以对神经元的输入和输出进行函数转换，从而改变神经网络的表达能力。不同的激活函数具有不同的特性，例如Sigmoid函数可以将输入映射到0-1之间，ReLU函数可以将输入映射到0以上的正数范围内。
3. 将处于无限域的输入变换到指定有限范围内的输出：激活函数可以将神经元的输入从无限域变换到指定的有限范围内，从而避免了输出值过大或者过小的问题。这对于神经网络的稳定性和泛化能力有很大的帮助。

损失函数则用来描述神经元的输出与实际标签之间的差异，这种差异也被称为损失值。

正向与反向传播神经网络

一个简单的神经网络由输入层（input layer），隐藏层（Hidden layer），输出层（output layer）构成

训练神经网络时，常采用反向传播（BP）算法更新神经元之间的权重。反向传播的过程可理解为根据损失函数的计算结果，沿着接近输出层到接近输入层的方向，逐层对权重和偏置量进行更新，以最小化损失值。调整的过程可以通过梯度下降等优化方法来实现。 层数较多的神经网络学习，被称为深度学习。

在线学习：每次正向传播都要求出误差，反向更新误差。

批处理学习：所有数据进行正向传播，利用误差总和对参数进行更新学习。

双层神经元理论和并联神经元理论

双层神经元理论，又称感知机模型，是一种早期的二元线性分类模型，包括一个输入层、一个或多个隐藏层和一个输出层，其中每一个隐藏层都由多个神经元组成。

并联神经元理论是一种改进的神经元模型，它通过增加隐藏层的神经元数量和/或增加隐藏层的层数来解决双层神经元理论的限制。并联神经元理论的核心思想是将多个神经元并联在一起，形成一个更复杂的模型，以处理更复杂的任务。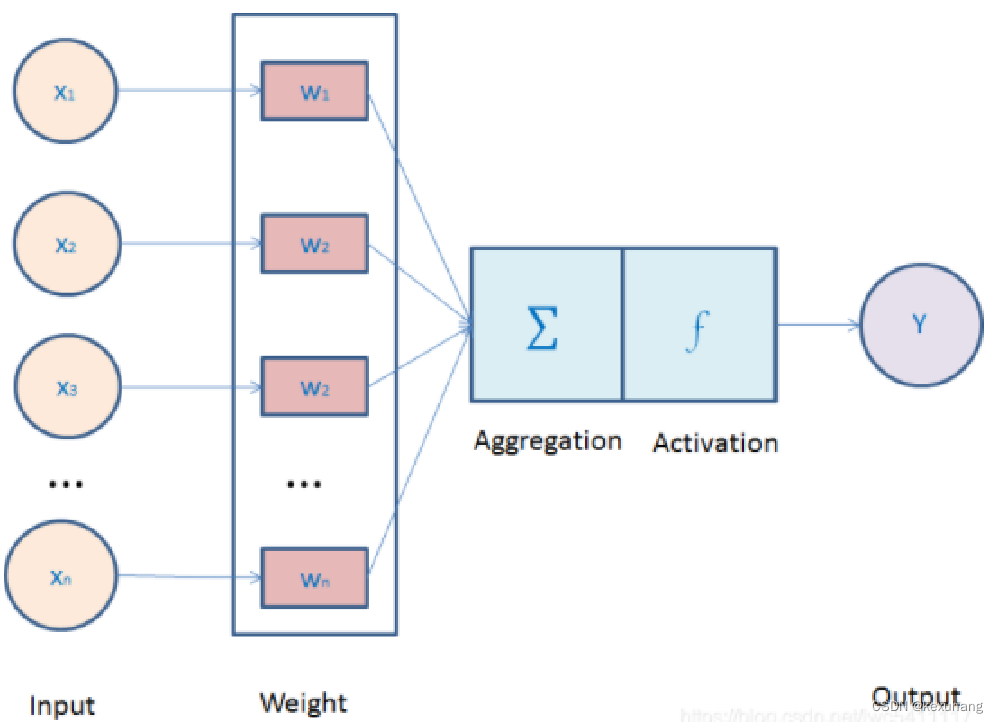

简单神经网络算法代码示例

#include <iostream>  
#include <cmath>  
  
using namespace std;  
  
// 神经元结构体  
struct Neuron {  
    double value; // 神经元值  
    double weight; // 权重  
};  
  
// 神经网络结构体  
struct NeuralNetwork {  
    Neuron inputLayer[3]; // 输入层  
    Neuron hiddenLayer[4]; // 隐藏层  
    Neuron outputLayer[2]; // 输出层  
};  
  
// 激活函数  
double activationFunction(double x) {  
    return 1 / (1 + exp(-x));  
}  
  
// 训练神经网络  
void trainNeuralNetwork(NeuralNetwork& nn, double input[], double target[]) {  
    // 前向传播  
    for (int i = 0; i < 3; i++) {  
        nn.inputLayer[i].value = input[i];  
    }  
    for (int i = 0; i < 4; i++) {  
        nn.hiddenLayer[i].value = 0;  
        for (int j = 0; j < 3; j++) {  
            nn.hiddenLayer[i].value += nn.inputLayer[j].value * nn.hiddenLayer[i].weight;  
        }  
        nn.hiddenLayer[i].value = activationFunction(nn.hiddenLayer[i].value);  
    }  
    for (int i = 0; i < 2; i++) {  
        nn.outputLayer[i].value = 0;  
        for (int j = 0; j < 4; j++) {  
            nn.outputLayer[i].value += nn.hiddenLayer[j].value * nn.outputLayer[i].weight;  
        }  
        nn.outputLayer[i].value = activationFunction(nn.outputLayer[i].value);  
    }  
  
    // 反向传播  
    for (int i = 0; i < 2; i++) {  
        double error = target[i] - nn.outputLayer[i].value;  
        for (int j = 0; j < 4; j++) {  
            nn.outputLayer[i].weight += error * nn.hiddenLayer[j].value;  
        }  
    }  
    for (int i = 0; i < 4; i++) {  
        double error = 0;  
        for (int j = 0; j < 2; j++) {  
            error += (target[j] - nn.outputLayer[j].value) * nn.outputLayer[j].weight;  
        }  
        error *= activationFunction(nn.hiddenLayer[i].value) * (1 - activationFunction(nn.hiddenLayer[i].value));  
        for (int j = 0; j < 3; j++) {  
            nn.hiddenLayer[i].weight += error * nn.inputLayer[j].value;  
        }  
    }  
}  
  
// 测试神经网络  
void testNeuralNetwork(NeuralNetwork& nn, double input[], double target[]) {  
    double output[2];  
    trainNeuralNetwork(nn, input, output);  
    cout << "Output: ";  
    for (int i = 0; i < 2; i++) {  
        cout << output[i] << " ";  
    }  
    cout << endl;  
}  
  
int main() {  
    // 初始化神经网络  
    NeuralNetwork nn;  
    for (int i = 0; i < 3; i++) {  
        nn.inputLayer[i].weight = rand() / double(RAND_MAX); // 随机权重  
    }  
    for (int i = 0; i < 4; i++) {  
        nn.hiddenLayer[i].weight = rand() / double(RAND_MAX); // 随机权重  
    }  
    for (int i = 0; i < 2; i++) {  
        nn.outputLayer[i].weight = rand() / double(RAND_MAX); // 随机权重  
    }

写一段神经网络算法的基本步骤

1.定义网络结构：确定网络的层数和每层的神经元数量，以及各层之间的连接方式。

2.初始化参数：随机初始化网络中的权重和偏置参数。

3.前向传播：根据输入的数据，通过前向传播计算每一层的输出值，直到最后一层。

4.计算损失：根据实际的标签和网络的输出值，计算损失函数的值。

5.反向传播：根据损失函数的值，通过反向传播计算每一层参数的梯度。

6.更新参数：根据梯度下降算法，更新网络中的权重和偏置参数。

7.重复训练：重复以上步骤，直到网络训练收敛或达到预设的迭代次数。

8.测试和评估：使用测试数据集对网络进行评估，计算网络的准确率、精度、召回率等指标