时间序列预测

问题简介

简单来说，时间序列是按照时间顺序，按照一定的时间间隔取得的一系列观测值，比如我们上边提到的国内生产总值，消费者物价指数，利率，汇率，股票价格等等。时间间隔可以是日，周，月，季度，年等。
那么如何进行时间序列分析分析呢？通常来说我们尝试找出序列值在过去所呈现的特征模式，假定这种模式在未来能够持续，进而对未来进行预测。时间序列基本特征包括：趋势性，序列相关性，随机性。

基本概念

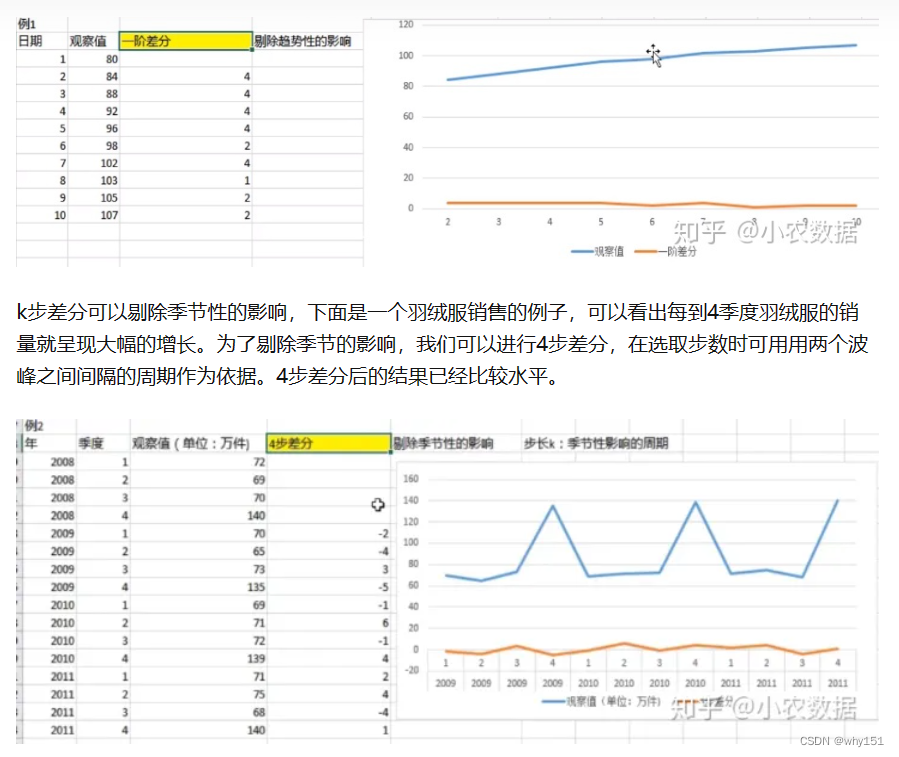
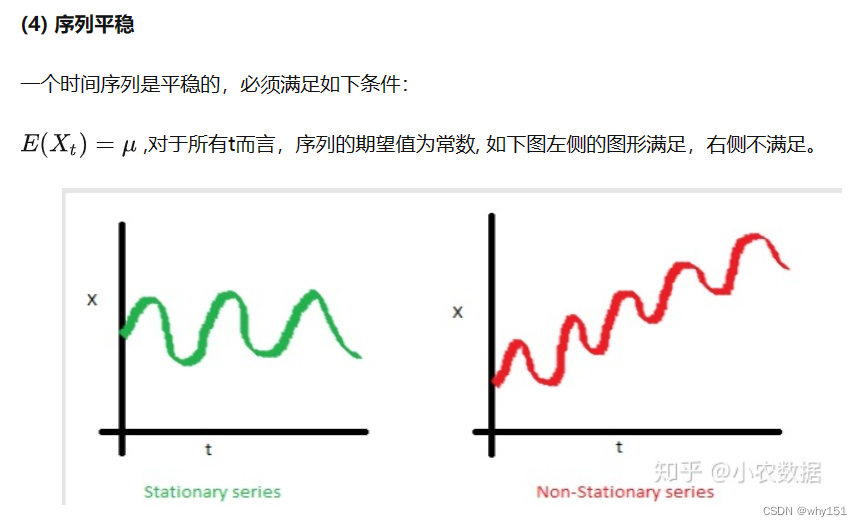
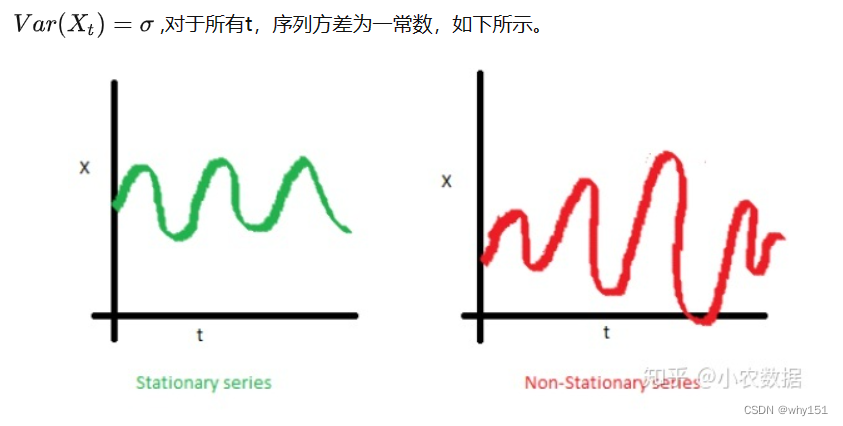
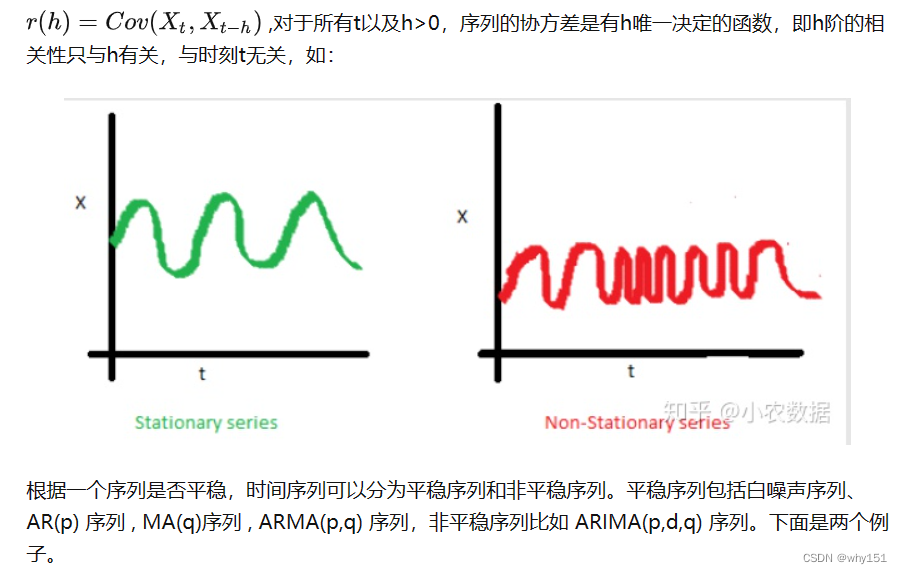
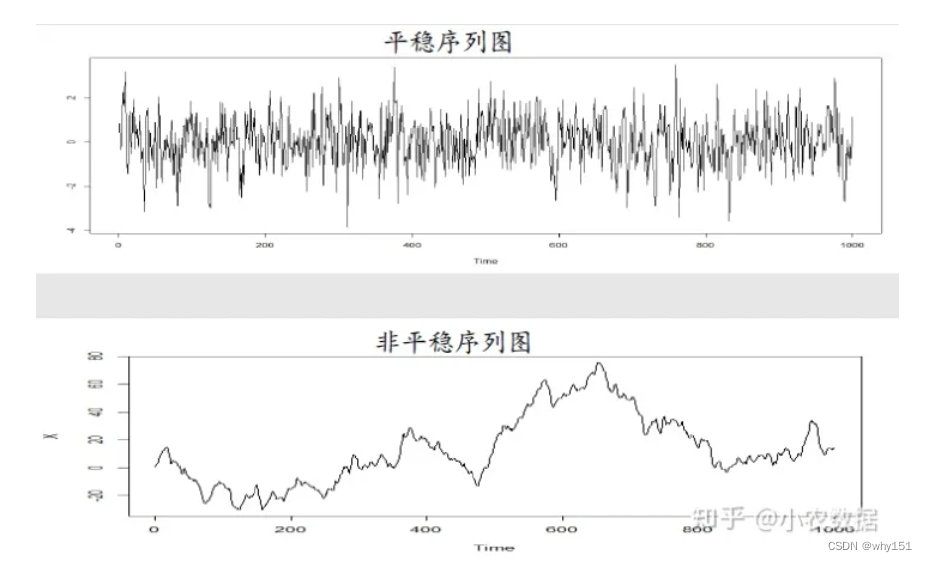
趋势性是指序列整体上呈现单调性，如平稳、上涨或下跌，先提一句，ARMA模型是平稳的时间序列模型，在建模前必须去除趋势性。
序列相关性是指当期的序列值和前期某个或某些序列值线性相关。
随机性是指序列在一定程度上呈现不确定性，由于模型并不能捕捉到现实世界中的所有特征，总会有一些噪声的存在，这些噪声我们称之为白噪声。
在这里插入图片描述

常用模型

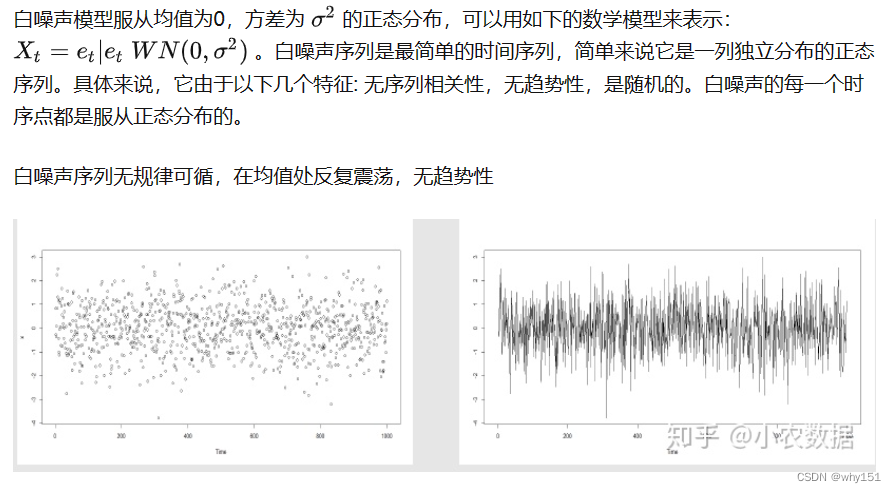
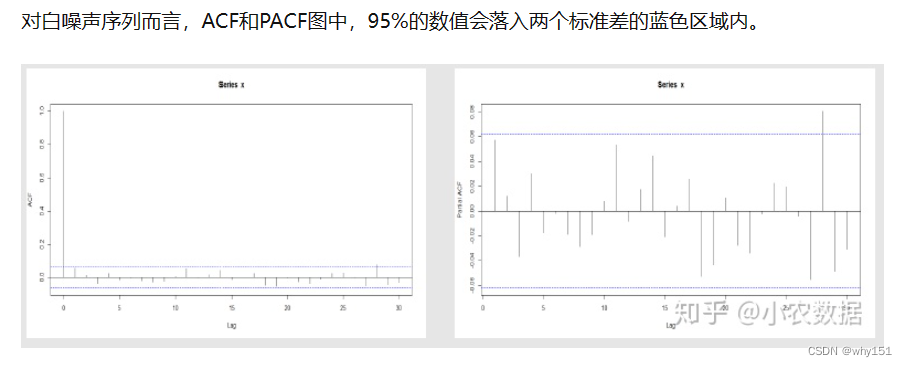
白噪声序列

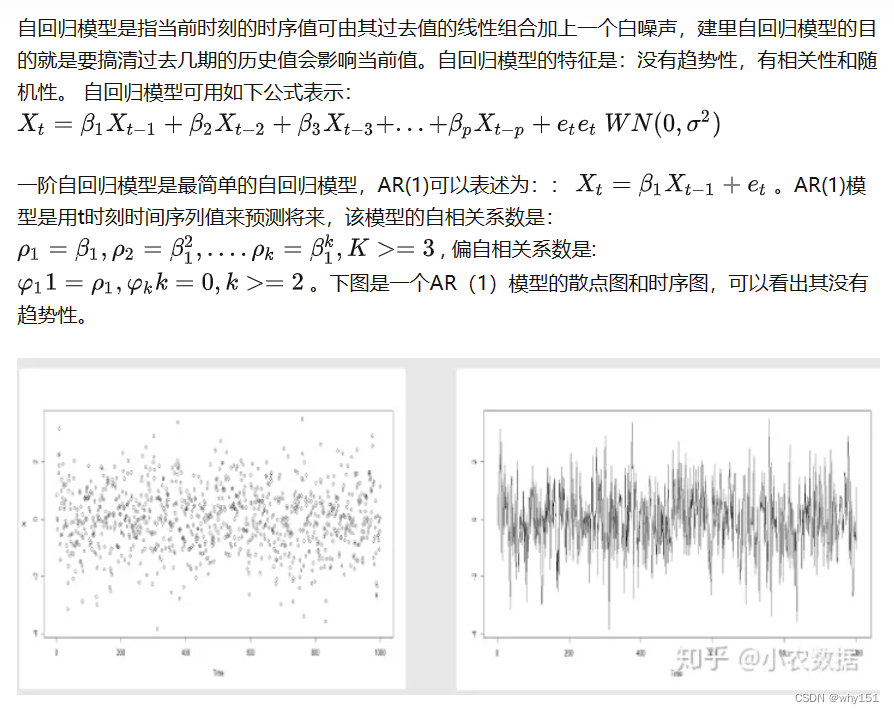
在这里插入图片描述

自回归模型

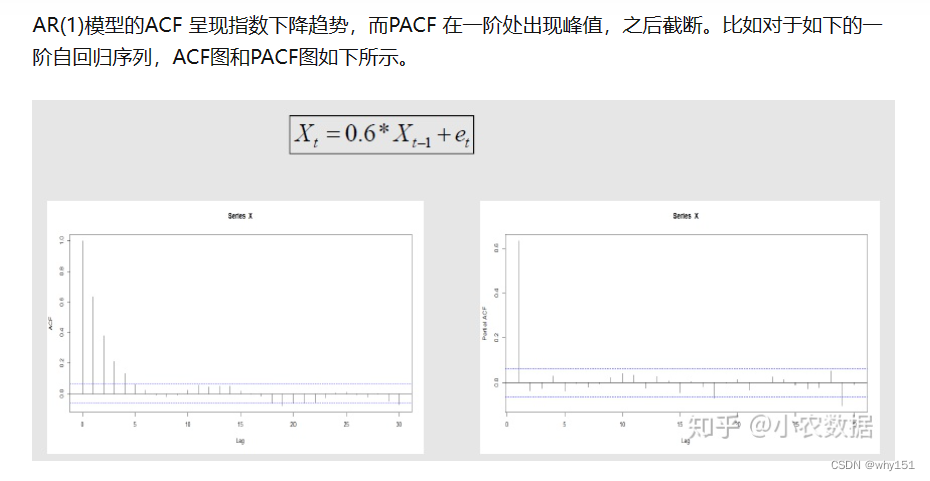
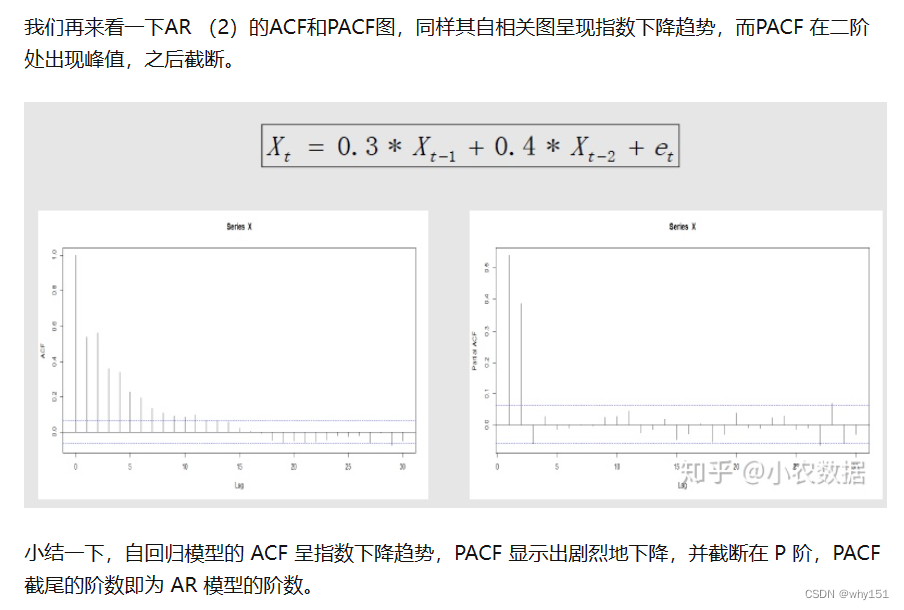
在这里插入图片描述

移动平均模型

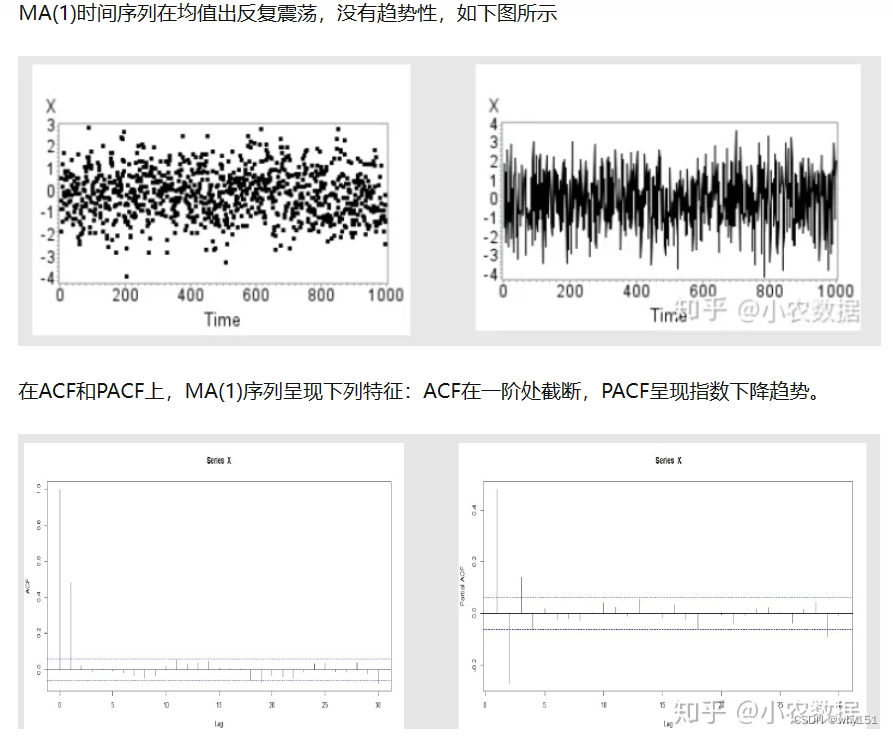
在这里插入图片描述

自回归移动平均模型

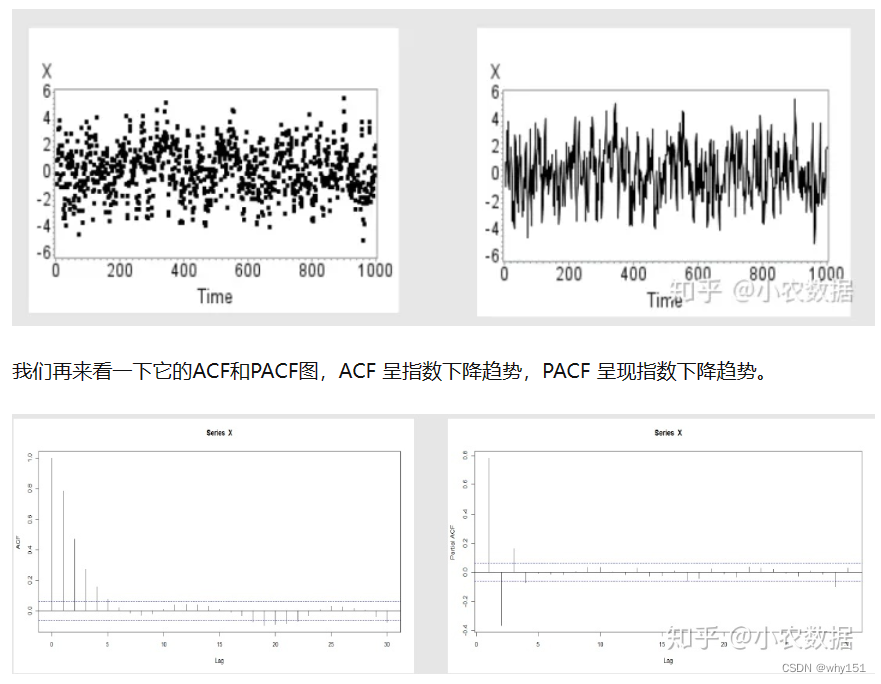
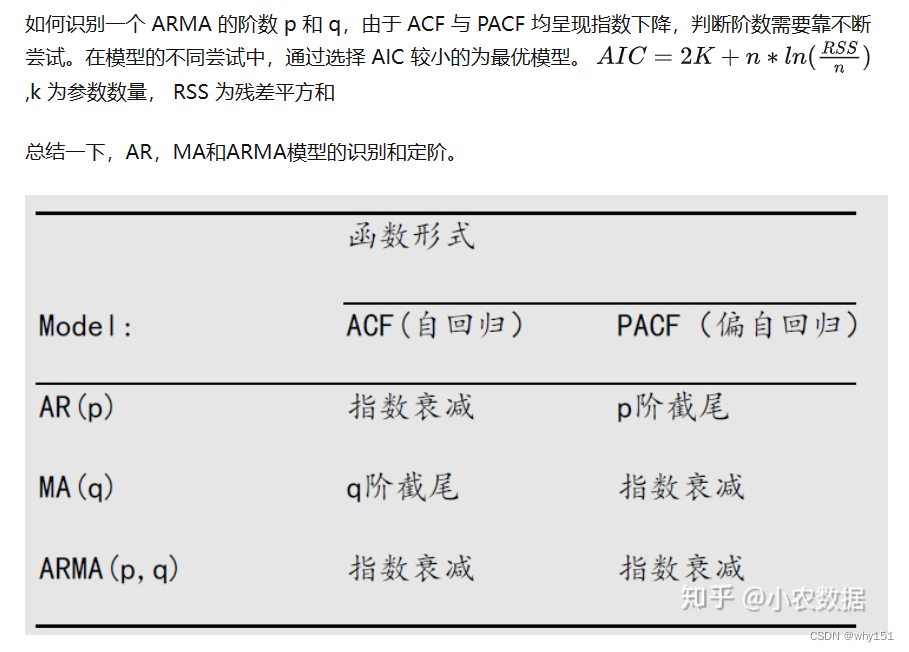
在这里插入图片描述

自回归求和移动平均模型(ARIMA)模型

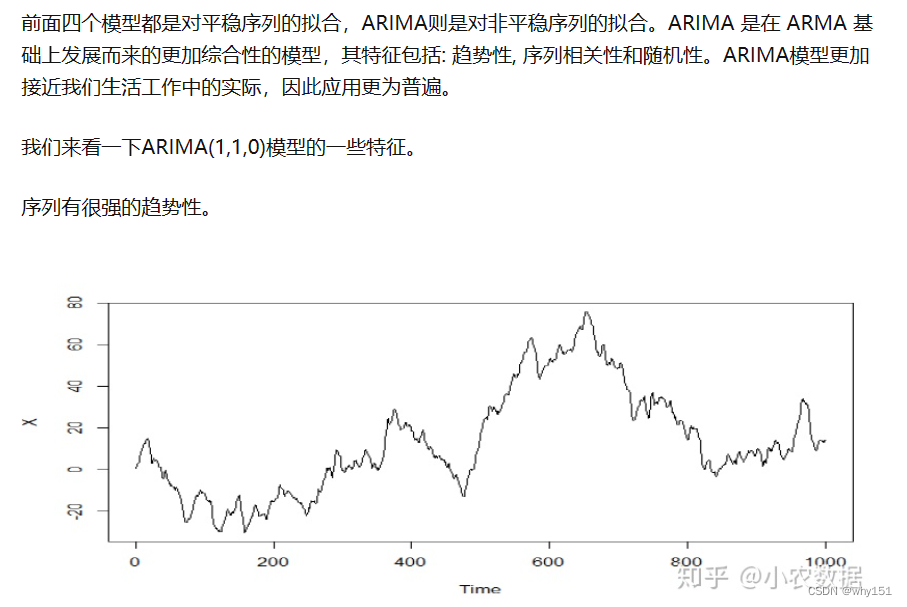
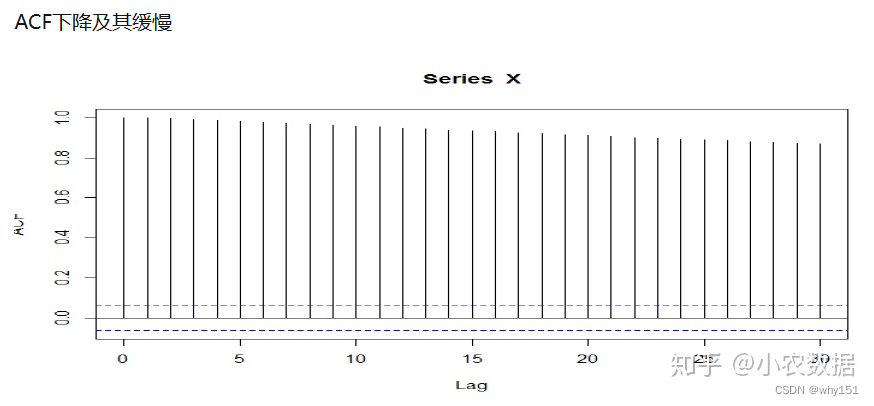
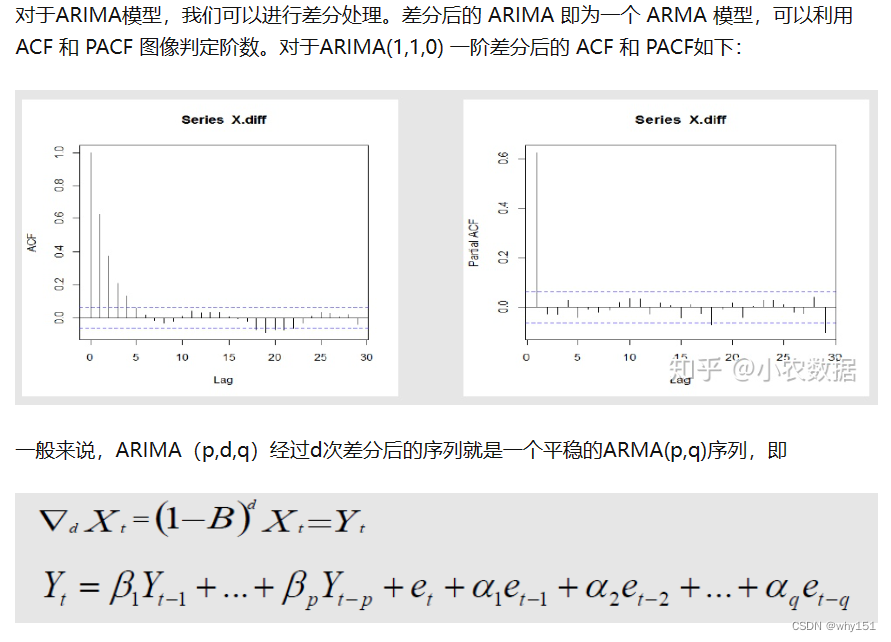
在这里插入图片描述

预测评价指标

ME （误差 ): Mean(Actual Predict)

MAE( 绝对误差 ) : Mean(abs(Actual Predict))

MAPE( 百分比误差 ): Mean(abs(Actual Predict)/Actual)

MSE( 均方误差平方和: Mean((Actual Predict)^2)

RMSE( 标准差）: Sqrt(Mean((Actual Predict)^2))

在评价指标的选取上，通常会结合分析的需求以及其他的时间序列模型方法，选择某个评价指标进而选择使该评价指标最小的模型方法。

Box-Jenkins建模流程

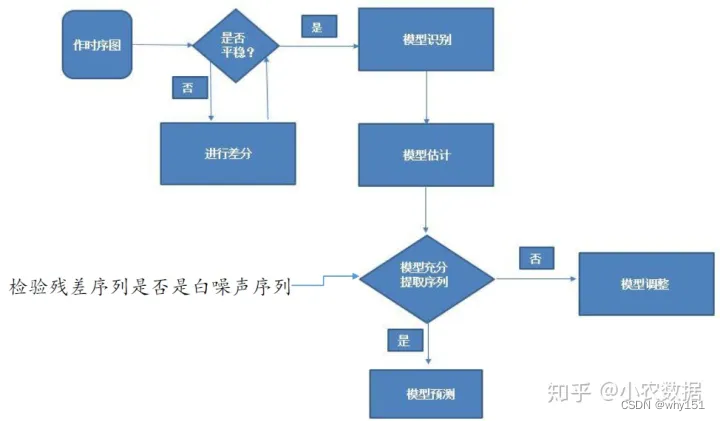
在这里插入图片描述
首先进行平稳性的判断，如果该序列是平稳的则直接进入第二步模型的识别，否则需要差分处理。在识别模型后，我们估计模型的参数。参数估计出来后我们要判断该模型的是否合理，主要通过检验残差序列是否为白噪声序列进行，白噪声序列是没有相关性的，也就意味着我们的模型已经把相关因素都提取出来了，可以用于后续的预测，否则我们的模型需要调整。最后我么能使用模型进行预测。下面我们具体来看一下每个步骤的细节：
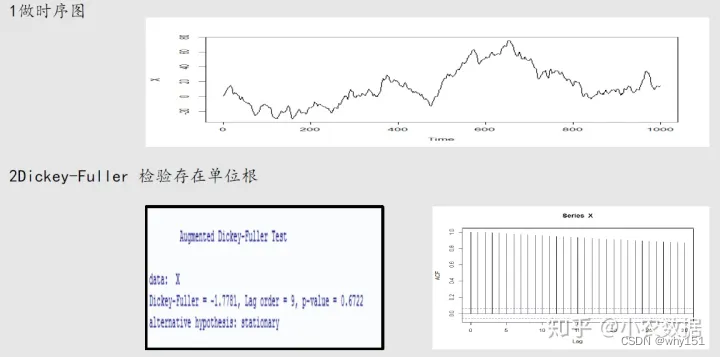
在这里插入图片描述

单位根检验

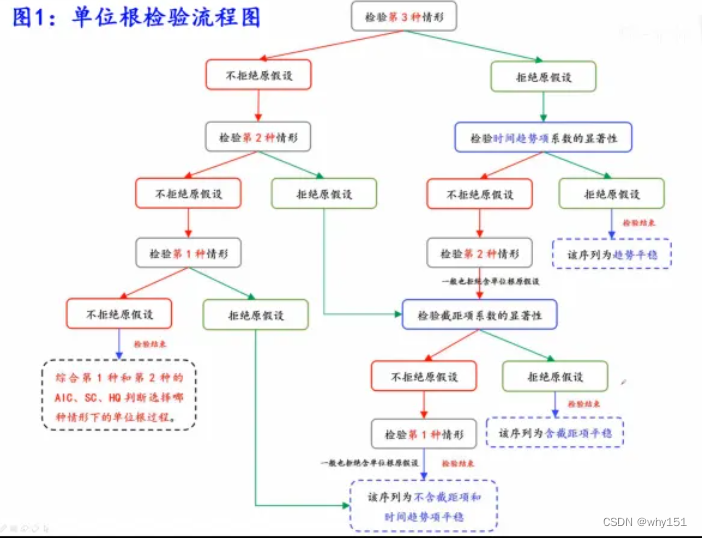
在这里插入图片描述

总结：单位根检验分为两种过程：平稳或者不平稳。
单位根检验的过程：先检验带截距和趋势的单位根过程，这时有两个结果。

检验显示平稳，那么应该搞清楚是什么状态的平稳，这时看时间趋势的检验结果，如果拒接原假设（不带趋势），那么检验结束，时间序列是趋势平稳，如果不拒接原假设，则认为不存在时间趋势，继续进行有截距的单位根检验，和时间趋势的检验相似，如果拒绝原假设（不带截距），可以判断时间序列截距平稳，这时如果不拒绝原假设，这时进行不带趋势和截距的单位根检验，检验结果一般平稳。
检验显示不平稳，直接进行带截距的单位根检验，如果结果平稳，则判断是什么状态的平稳，如果不平稳继续进行检验，即不带截距和趋势的单位根检验，根据AIC,BC和SIC最小的个数判断是什么单位根过程。 ADF python操作

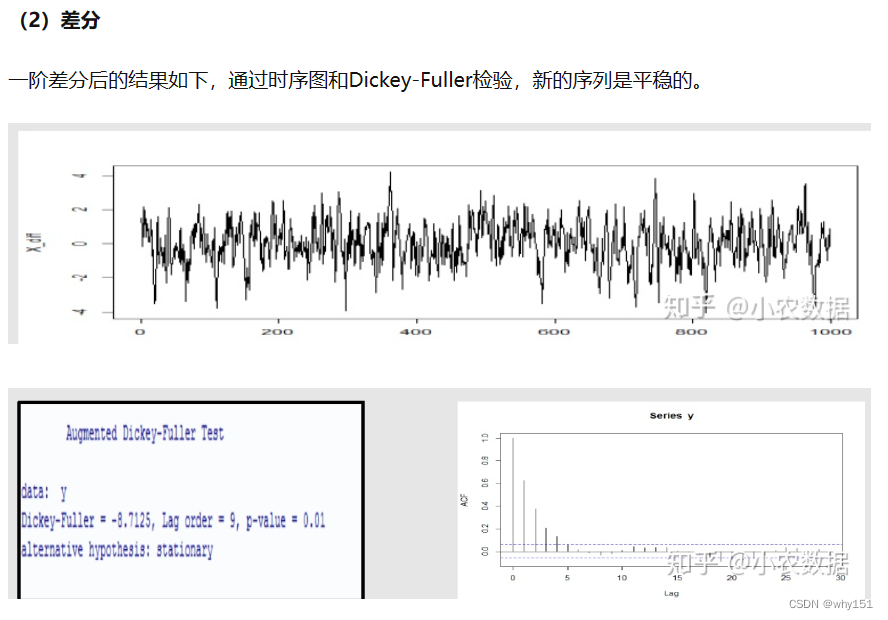
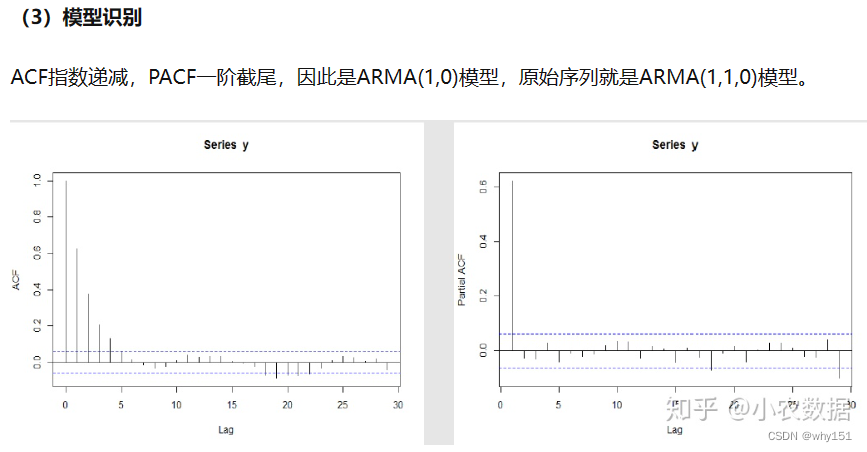
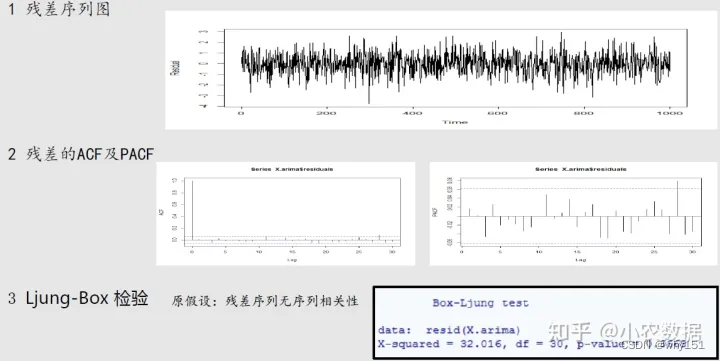
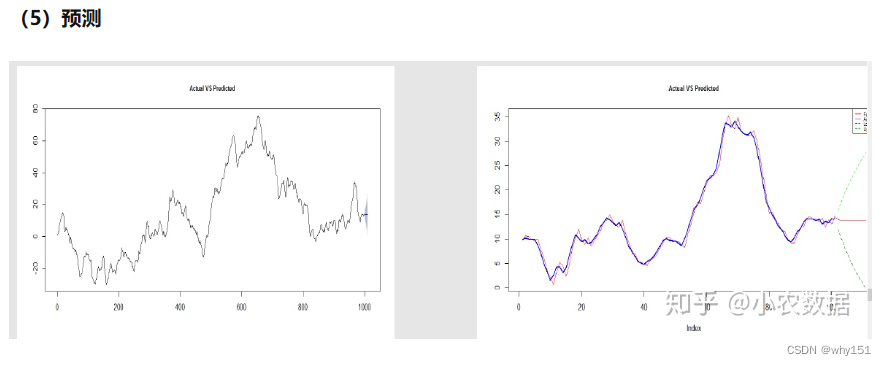
深度学习方法

LSTM

循环神经网络

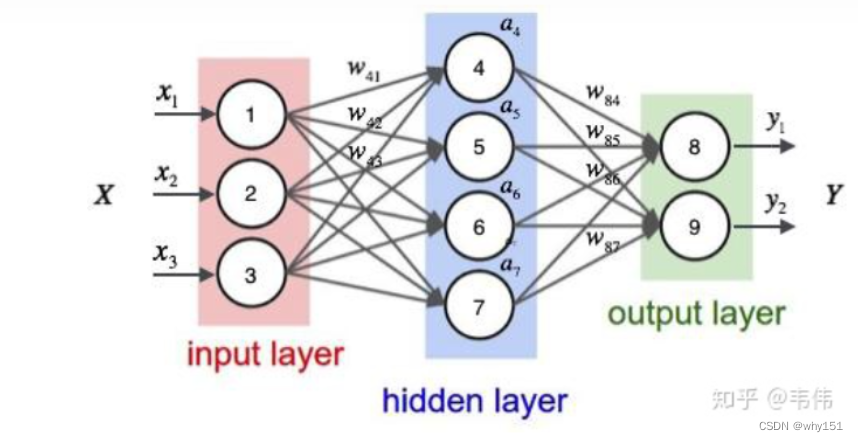
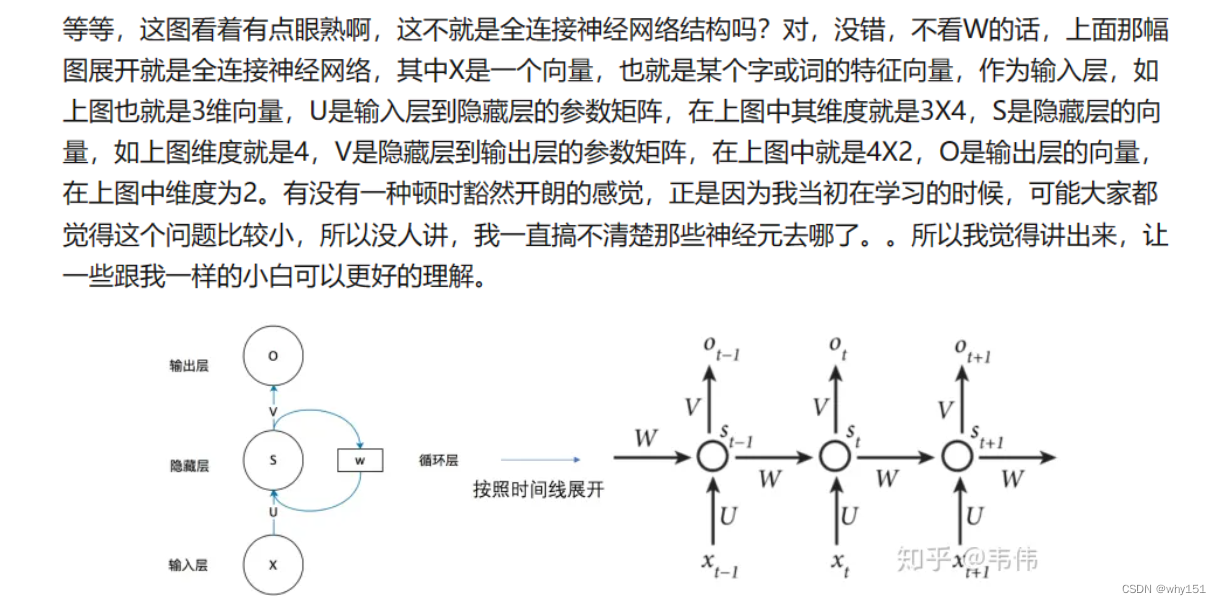
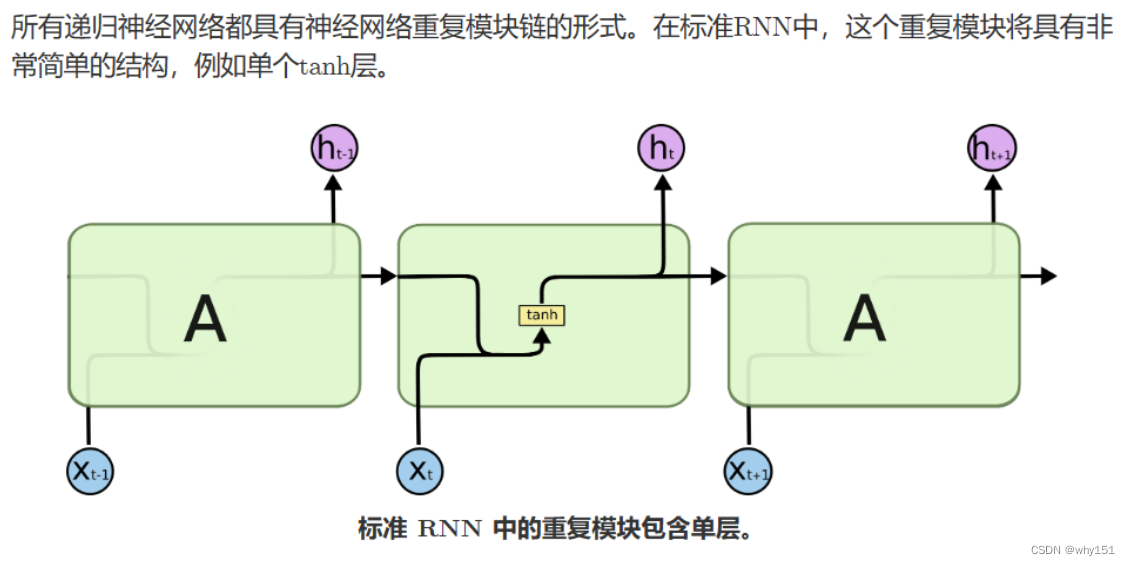
相较于循环神经网络大家应该更熟悉全连接神经网络和卷积神经网络，以及它们的训练和使用。他们都只能单独的取处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。比如，当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。这时，就需要用到深度学习领域中另一类非常重要神经网络：**循环神经网络(Recurrent Neural Network)**。
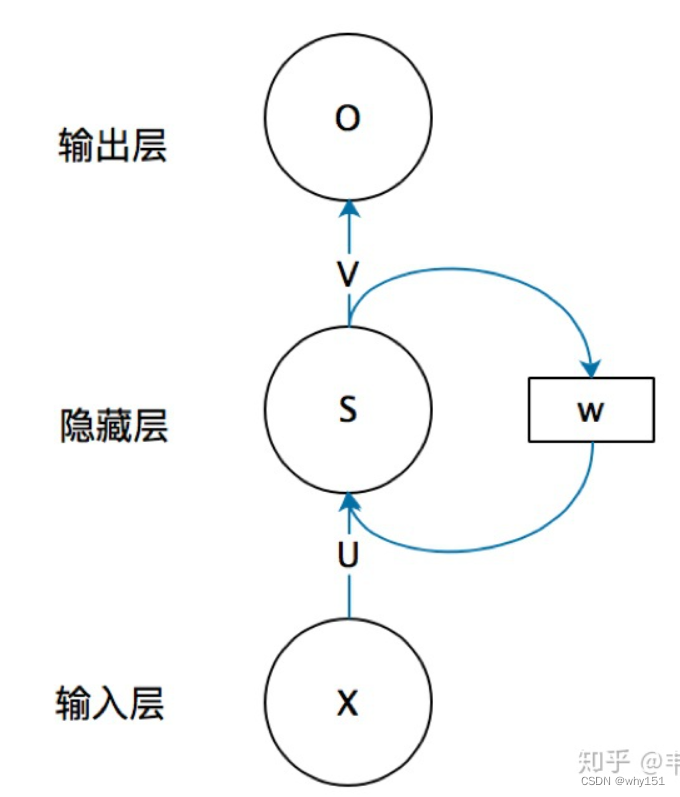
在这里插入图片描述

LSTM

为什么LSTM优于RNN?

这里就牵扯到梯度消失和爆炸的问题了，上面那个最基础版本的RNN，我们可以看到，每一时刻的隐藏状态都不仅由该时刻的输入决定，还取决于上一时刻的隐藏层的值，如果一个句子很长，到句子末尾时，它将记不住这个句子的开头的内容详细内容。

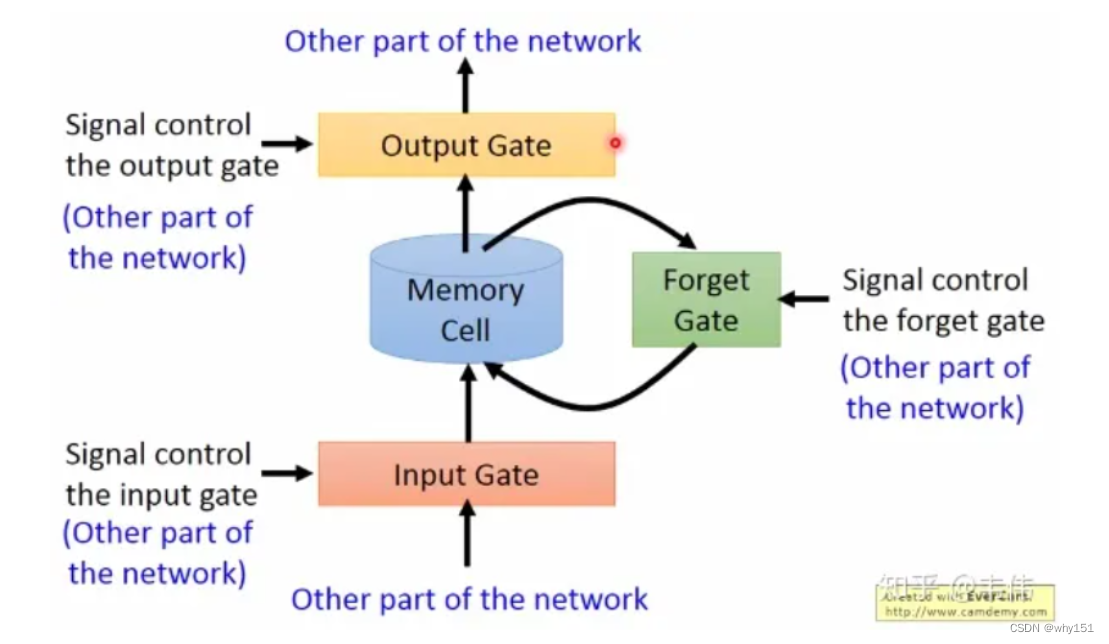
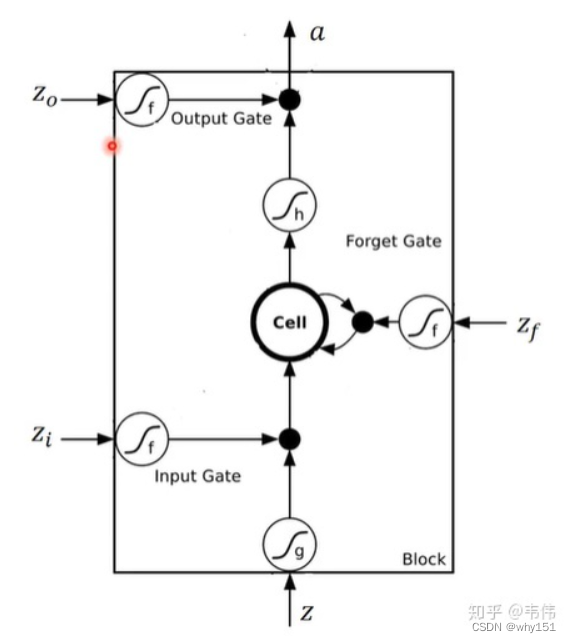
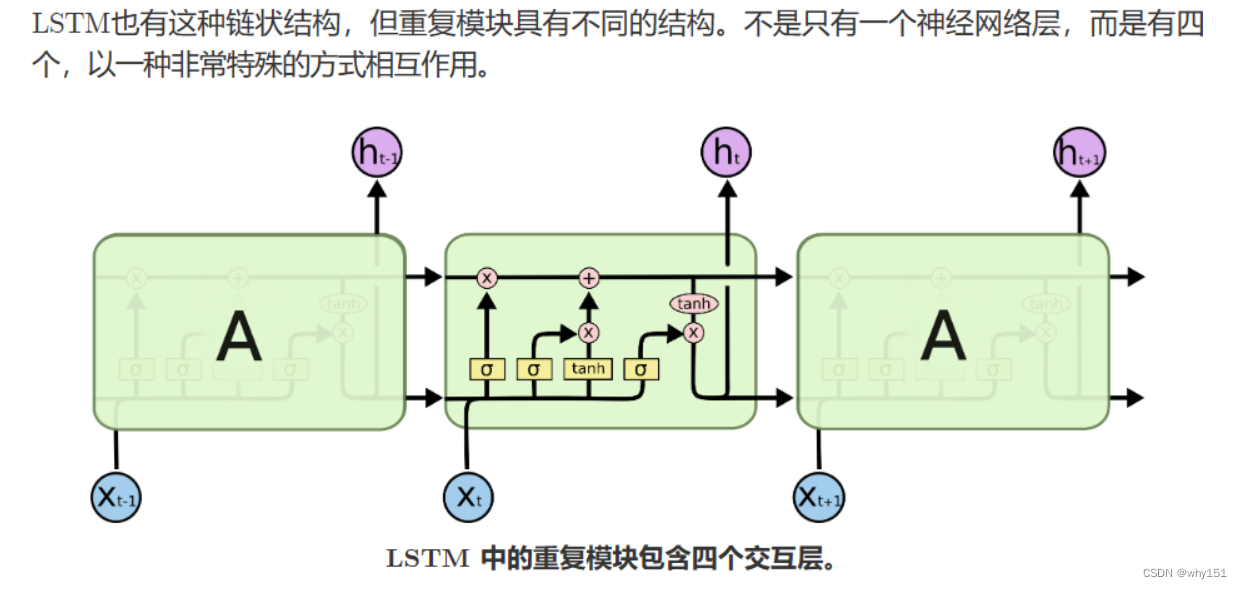
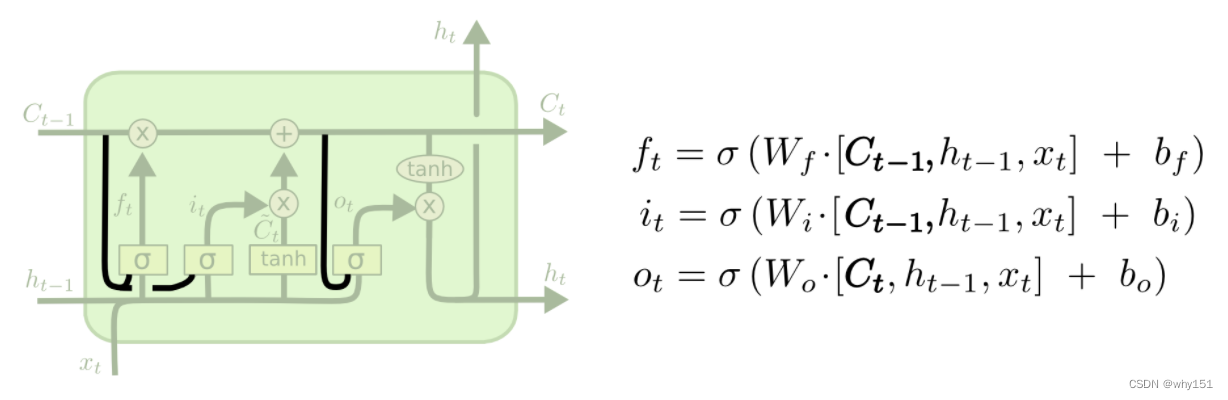
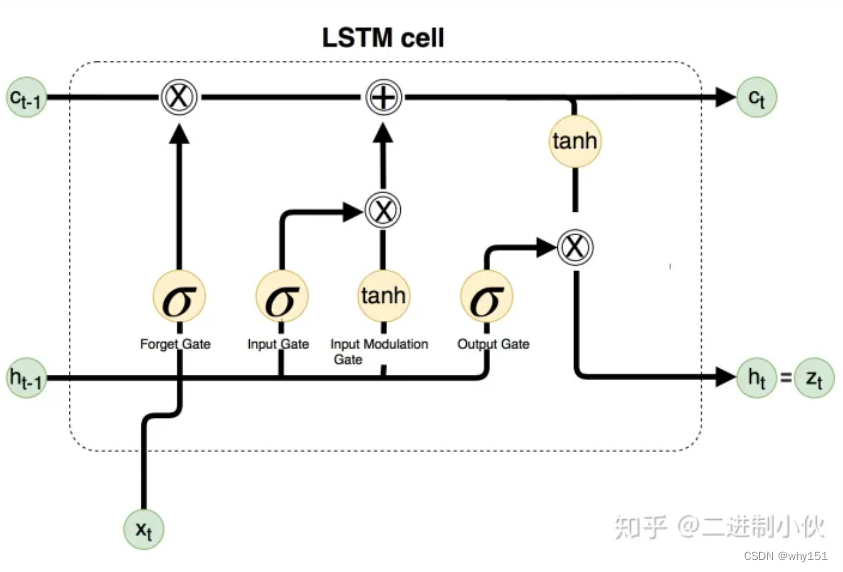
LSTM通过它的“门控装置”有效的缓解了这个问题，这也就是为什么我们现在都在使用LSTM而非普通RNN。
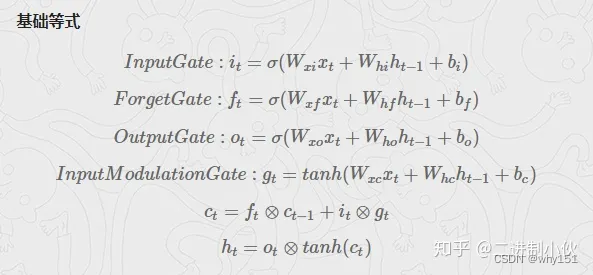
在这里插入图片描述

优化思路

1.利用优化算法（粒子群、遗传算法…）优化超参数

2.优化误差反向传播过程中的经典随机梯度下降算法（Adam）

多层LSTM（nested two(n)-layer LSTM model）

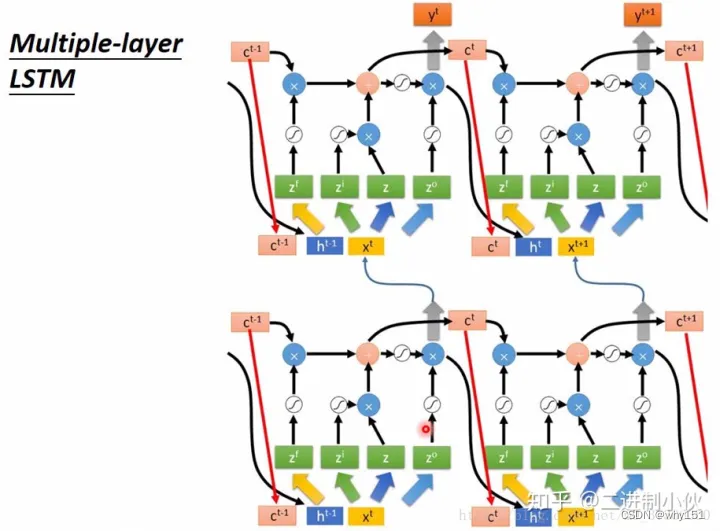
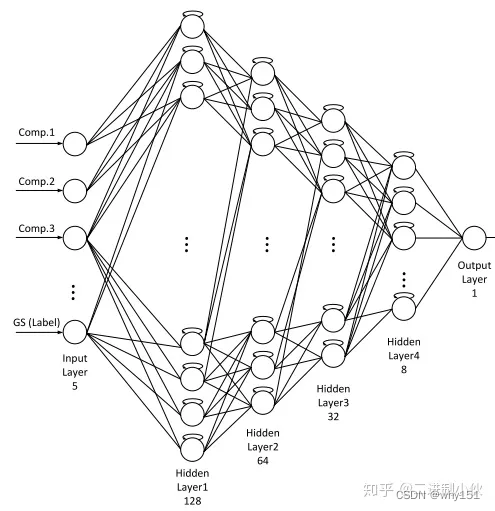
在这里插入图片描述

双向LSTM（Bi-LSTM）

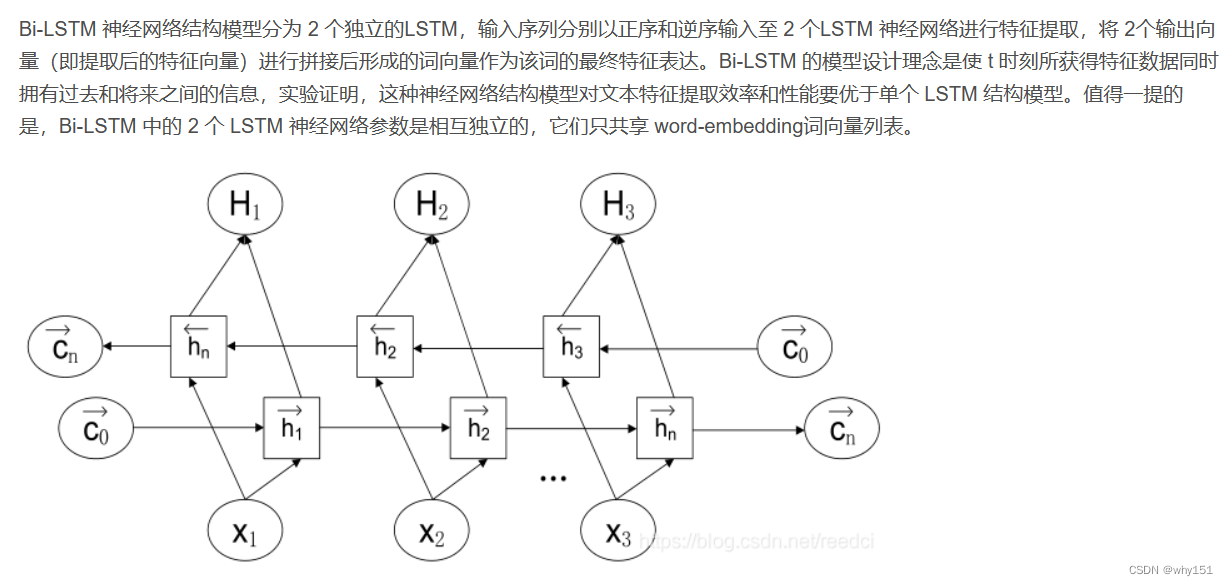
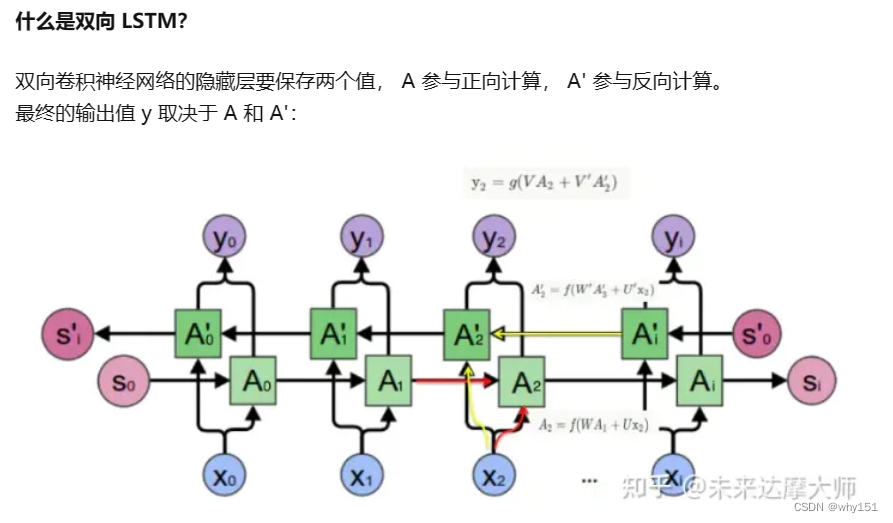
在这里插入图片描述

即正向计算时，隐藏层的

     s
    
    
     t
    
   
  
  
   s_t
  
 
st 与 

 
  
   
    
     s
    
    
     
      t
     
     
      －
     
     
      1
     
    
   
  
  
   s_{t－1}
  
 
st－1 有关；反向计算时，隐藏层的 

 
  
   
    
     s
    
    
     t
    
   
  
  
   s_t
  
 
st 与

 
  
   
    
     s
    
    
     
      t
     
     
      ＋
     
     
      1
     
    
   
  
  
   s_{t＋1}
  
 
st＋1 有关：

在这里插入图片描述
文末有python例子

随机LSTM（RLSTM）

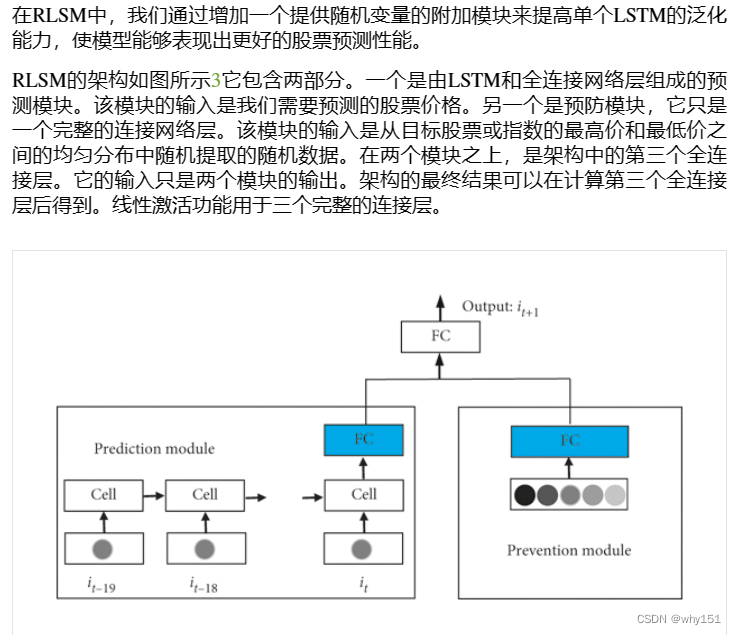
在这里插入图片描述
参考文献

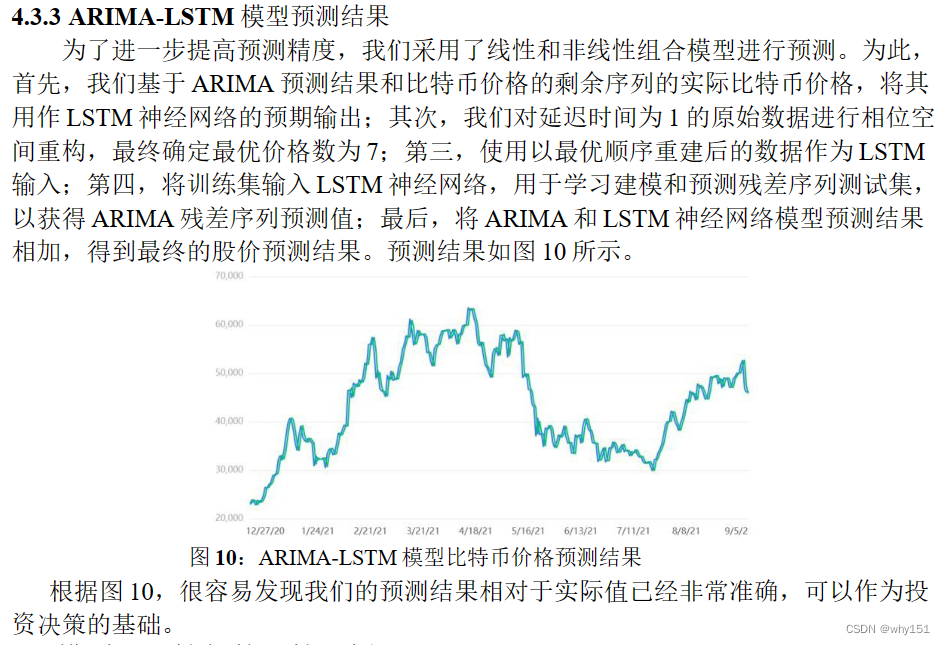
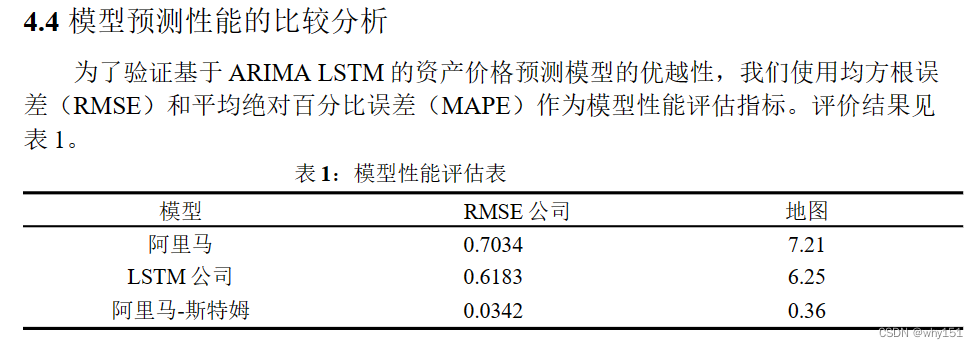
ARIMA-LSTM（2022 C 2212336）

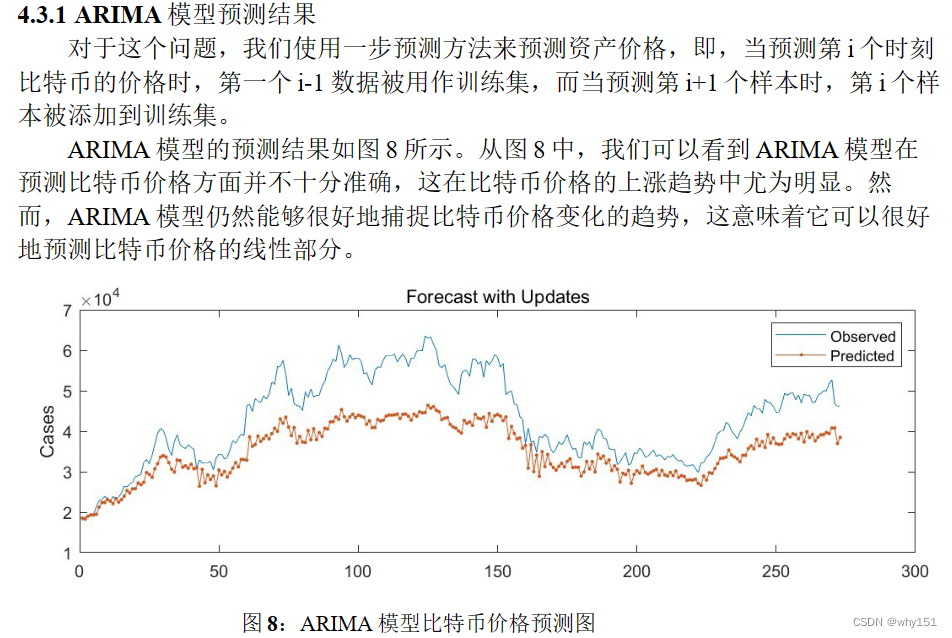
在这里插入图片描述

相空间重构模型

在时间序列问题的一般场景中，都是通过在时间域或者时域与频域的变换中进行研究的，而有一类时间序列本身是在确定系统中出现的无规则的运动极具混沌特性的时间序列(混沌的含义是混乱而没有秩序的状态)，这个混沌现象是广泛存在的，因为很多后续变化都是对初值敏感，而且虽然整个过程中表面无规则但是实际上是可以通过一些动力学模型预测的。对于这一类混沌时间序列的问题(包括模型建立和预测)在现存的理论中是在相空间进行研究的，所以自然而然相空间重构是处理混沌时间序列中非常重要的过程。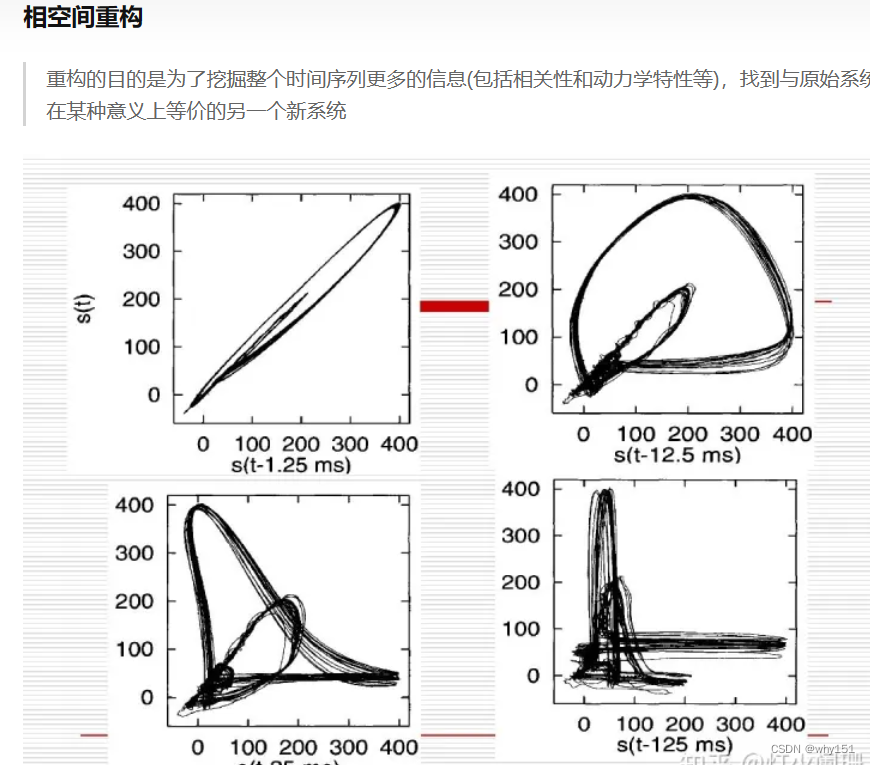
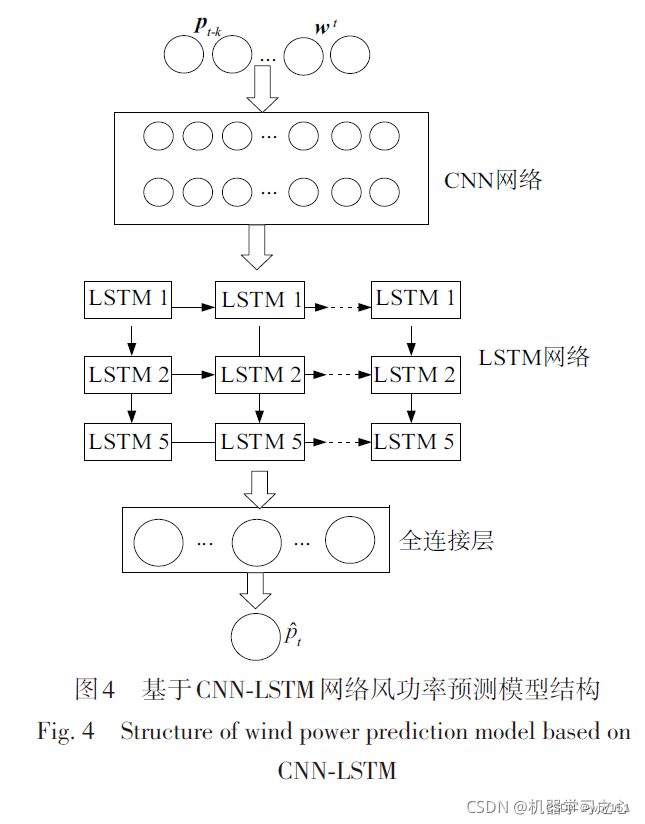
在这里插入图片描述