牛客网《剑指offer》专栏刷题练习之二叉树合集

✅作者简介：热爱后端语言的大学生，CSDN内容合伙人
✨精品专栏：C++面向对象
🔥系列专栏：剑指offer
📃推荐一款模拟面试、刷题神器👉注册免费刷题

二叉树题解目录

🔥前言

本篇文章给大家分享牛客网《剑指offer》专栏中有关二叉树的经典算法题解，我会按照自己的理解与思路帮助大家搞懂算法流程。

1、二叉树的下一个结点

1.1、题目速览

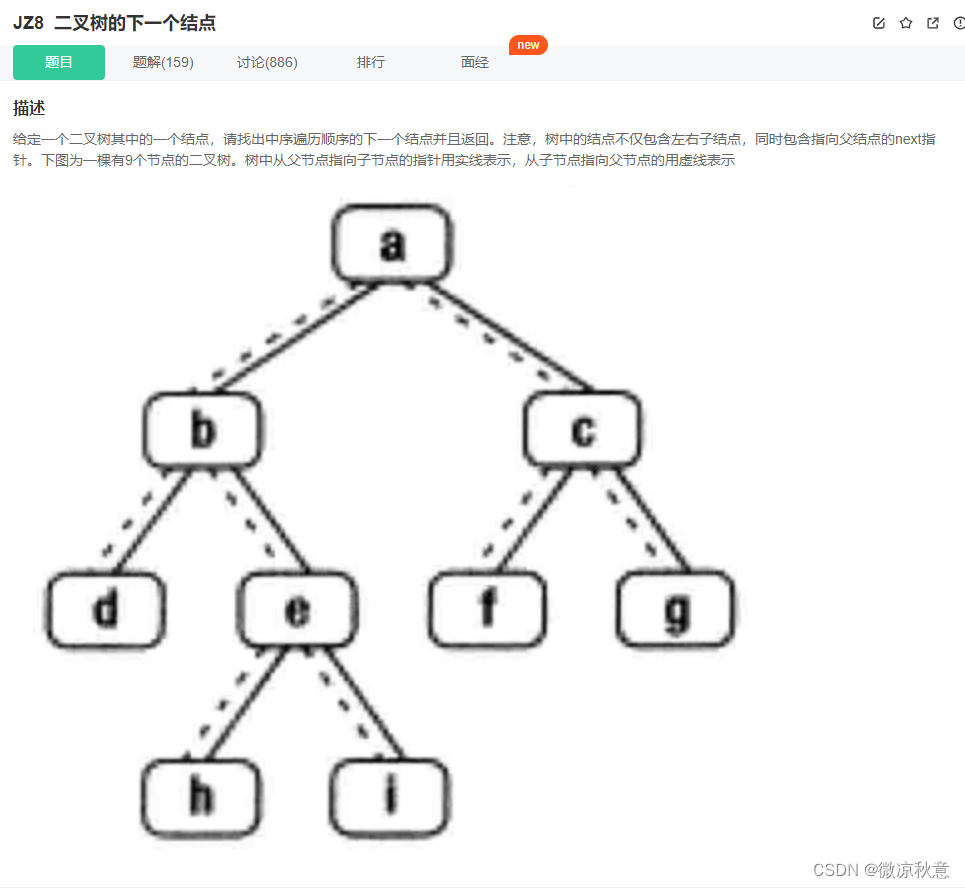
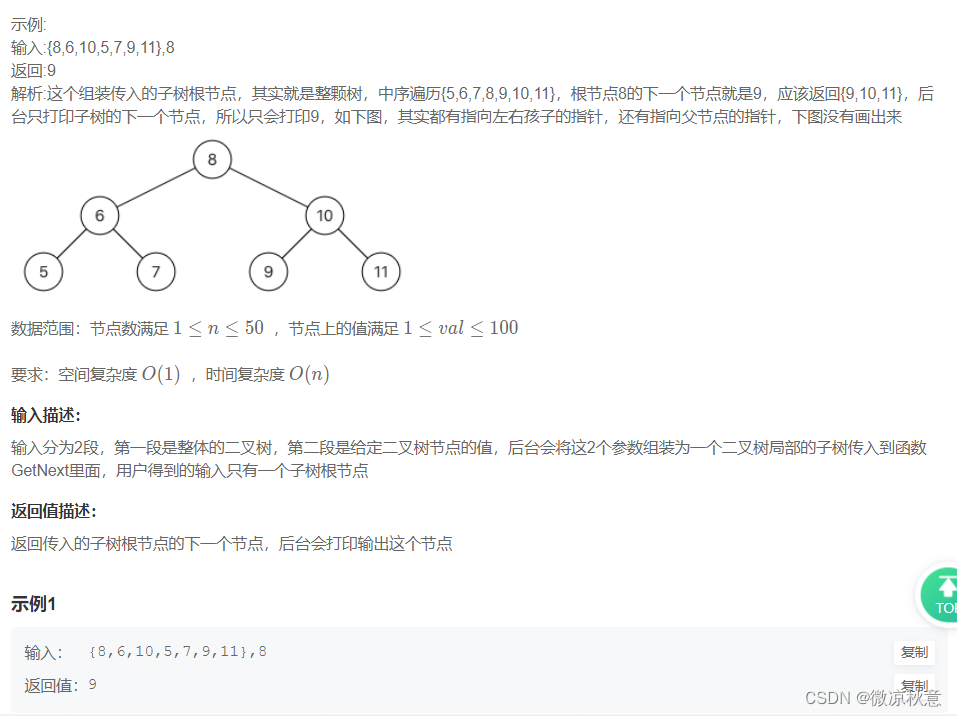
1.2、个人题解

1.2.1、解题思路

1. 我们首先要根据给定输入中的结点指针向父级进行迭代，直到找到该树的根节点；
2. 然后根据根节点进行中序遍历，当遍历到和给定树节点相同的节点时，下一个节点就是我们的目标返回节点

具体步骤：

1. 根据当前结点，利用题目所给条件找到根结点
2. 书写中序遍历的函数，传入根结点
3. 将中序遍历的结点储存在结点数组里
4. 将传入的二叉树结点与数组元素匹配，返回数组的下一个元素

1.2.2、代码实现

/*
struct TreeLinkNode {
    int val;
    struct TreeLinkNode *left;
    struct TreeLinkNode *right;
    struct TreeLinkNode *next;
    TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {
        
    }
};
*/classSolution{public:
    vector<TreeLinkNode*>nodes;
    TreeLinkNode*GetNext(TreeLinkNode* pNode){
        TreeLinkNode* root=pNode;//利用父指针找到根结点while(root->next)    
            root=root->next;//调用中序遍历InOrder(root);int num=nodes.size();for(int i=0;i<num;i++){
            TreeLinkNode *cur=nodes[i];if(pNode==cur){return nodes[i+1];}}returnNULL;}//书写中序遍历voidInOrder(TreeLinkNode* root){if(root==NULL)return;InOrder(root->left);
        nodes.push_back(root);InOrder(root->right);}};

1.2.3、代码解析

• 首先创建动态数组nodes，注意是创建在方法外部，目的是可以在类内任意使用
• 创建的root结点并借助while循环通过父指针next找到根结点
• 书写InOrder中序遍历函数，将中序遍历结果存入上方创建的nodes数组中
• 使用for循环将传入结点pNode与数组元素比较，如果匹配到就返回位置加一的结点

2、对称的二叉树

2.1、题目速览

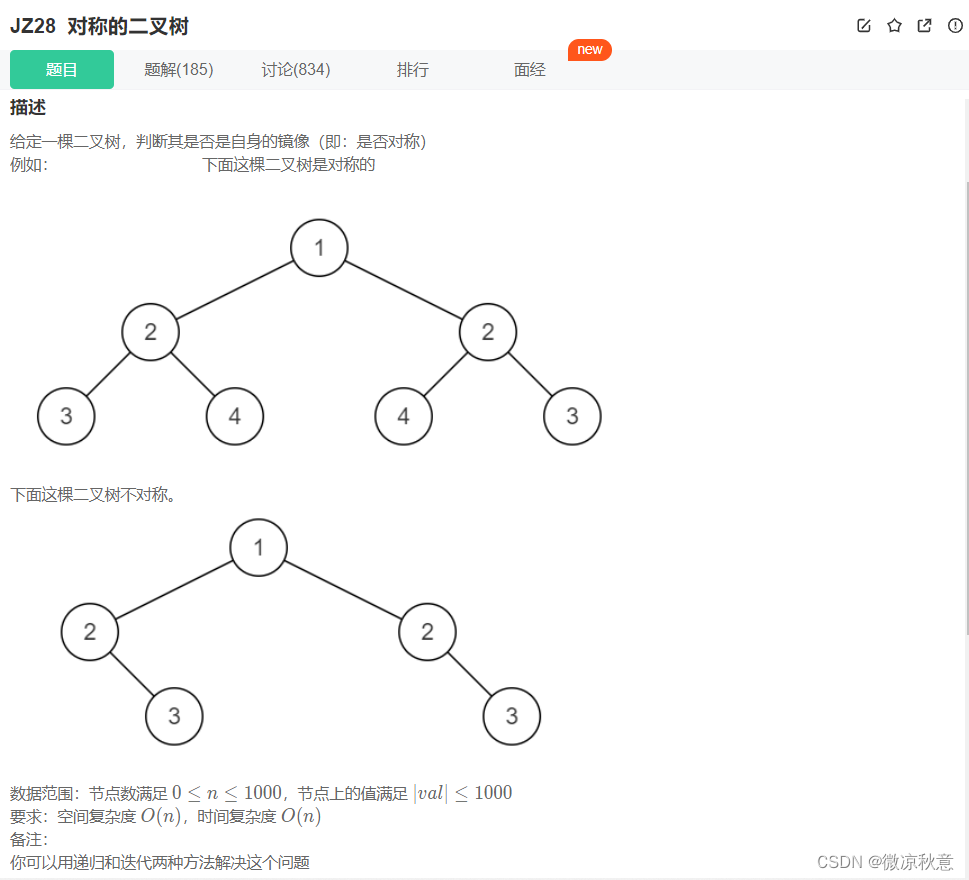
2.2、个人题解

2.2.1、解题思路

前序遍历的时候我们采用的是“根左右”的遍历次序，如果这棵二叉树是对称的，即相应的左右节点交换位置完全没有问题；
那我们是不是可以尝试“根右左”遍历，按照轴对称图像的性质，这两种次序的遍历结果应该是一样的。
但是如果相同的方式进行两次，可行但我们不去做，这对时间的消耗太多了，我们不如在遍历的过程就结果比较了。而遍历方式依据前序递归可以使用递归：

1. 两种方向的前序遍历，同步过程中的当前两个节点，同为空，属于对称的范畴。
2. 当前两个节点只有一个为空或者节点值不相等，已经不是对称的二叉树了。
3. 第一个节点的左子树与第二个节点的右子树同步递归对比，第一个节点的右子树与第二个节点的左子树同步递归比较。

2.2.2、代码实现

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/classSolution{public:boolisSymmetrical(TreeNode* pRoot){returndgfunc(pRoot,pRoot);}booldgfunc(TreeNode* root1,TreeNode* root2){if(root1==NULL&&root2==NULL)returntrue;if(root1==NULL||root2==NULL||root1->val!=root2->val)returnfalse;returndgfunc(root1->left, root2->right)&&dgfunc(root1->right,root2->left);}};

2.2.3、代码解析

• 编写dgfunc函数，将pRoot传入比较
• 前两个if是递归结束的条件： - 如果结点相同返回true- 如果一边为NULL或者左子树与右子树不同，返回false
• 调用递归，比较左右子树，都相同就返回true，不相同则返回false

还是那句话，牵扯到二叉树就尽量使用递归的方法来解决问题！