复习--范数
范数
范数和赋范矢量空间的认识
范数是一个具有“长度”概念的函数。在线性代数、范函分析及相关的数学领域里,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。定义范数的矢量空间就是赋范矢量空间。
范数赋范矢量空间的数学定义
f
∈
S
若存在唯一实数
∥
⋅
∥
f \in S 若存在唯一实数 \lVert \cdot \rVert
f∈S若存在唯一实数∥⋅∥满足
- 正定性: f ≥ 0 , 当且仅当 f = 0 , ∥ f ∥ = 0 f \geq 0 ,当且仅当 f = 0, \lVert f \rVert = 0 f≥0,当且仅当f=0,∥f∥=0
- 其次性: ∀ a ∈ R , ∥ a f ∥ = ∣ a ∣ ⋅ ∥ f ∥ \forall a \in R ,\lVert a f \rVert = \lvert a \rvert \cdot \lVert f \rVert ∀a∈R,∥af∥=∣a∣⋅∥f∥
- 三角不等式: ∥ f + g ∥ ≤ ∥ f ∥ + ∥ g ∥ , f , g ∈ S \lVert f + g \rVert \leq \lVert f \rVert + \lVert g \rVert , f,g \in S ∥f+g∥≤∥f∥+∥g∥,f,g∈S 则称 ∥ ⋅ ∥ ,是线性空间 S 上的范数,线性空间 S 则称为赋范线性空间。 则称\lVert \cdot \rVert,是线性空间 S 上的范数,线性空间 S 则称为赋范线性空间。 则称∥⋅∥,是线性空间S上的范数,线性空间S则称为赋范线性空间。
向量范数的数学定义
R
n
空间的向量范数
∥
⋅
∥
指的是一个
R
n
→
R
的函数,对任意的
x
,
y
∈
R
n
满足下列条件
R^n 空间的向量范数 \lVert \cdot \rVert 指的是一个 R^n \to R 的函数,对任意的 x, y \in R^n 满足下列条件
Rn空间的向量范数∥⋅∥指的是一个Rn→R的函数,对任意的x,y∈Rn满足下列条件
∥ x ∥ ≥ 0 , ∥ x ∥ = 0 当且仅当 x = 0 (正定性) \lVert x \rVert \geq 0, \lVert x \rVert = 0 当且仅当 x = 0(正定性) ∥x∥≥0,∥x∥=0当且仅当x=0(正定性)∥ a x ∥ = ∣ a ∣ ⋅ ∥ x ∥ , ∀ a ∈ R (其次性) \lVert a x \rVert = \lvert a \rvert \cdot \lVert x \rVert,\forall a \in R (其次性) ∥ax∥=∣a∣⋅∥x∥,∀a∈R(其次性)∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥ (三角不等式) \lVert x + y \rVert \leq \lVert x \rVert + \lVert y \rVert (三角不等式) ∥x+y∥≤∥x∥+∥y∥(三角不等式)
集中常见的向量范数
向量的 ∞ − 范数: ∥ x ∥ ∞ = max 1 ≤ i ≤ n ∣ x i ∣ 向量的\infty-范数:\lVert x \rVert_\infty = \operatorname*{max}_{1 \leq i \leq n}{\lvert x_i \rvert} 向量的∞−范数:∥x∥∞=1≤i≤nmax∣xi∣向量的 1 − 范数: ∥ x ∥ i = ∑ i = 1 n ∣ x i ∣ 向量的1- 范数:\lVert x \rVert_i = \sum_{i=1}^{n}{\lvert x_i \rvert} 向量的1−范数:∥x∥i=i=1∑n∣xi∣向量的 2 − 范数: ∥ x ∥ 2 = ( ∑ i = 1 n x 2 ) 1 2 向量的2- 范数:\lVert x \rVert_2 = (\sum_{i=1}^{n}{x^2})^{\frac{1}{2}} 向量的2−范数:∥x∥2=(i=1∑nx2)21向量的 p − 范数: ∥ x ∥ p = ( ∑ i = 1 n ∣ x ∣ p ) 1 p 向量的p- 范数:\lVert x \rVert_p = (\sum_{i=1}^{n}{\lvert x \rvert^p})^{\frac{1}{p}} 向量的p−范数:∥x∥p=(i=1∑n∣x∣p)p1
矩阵范数的数学定义
如果矩阵
A
∈
R
m
×
n
的某个非负的实值函数
∥
⋅
∥
满足:
如果矩阵 A \in R^{m \times n} 的某个非负的实值函数\lVert \cdot \rVert 满足:
如果矩阵A∈Rm×n的某个非负的实值函数∥⋅∥满足:
- 正定性: ∥ A ∥ ≥ 0 , ∥ A ∥ = 0 但且仅当 A = O \lVert A \rVert \geq 0, \lVert A \rVert = 0但且仅当 A = O ∥A∥≥0,∥A∥=0但且仅当A=O
- 其次性: ∥ a A ∥ = ∣ a ∣ ⋅ ∥ A ∥ ,对任意的 a ∈ R \lVert a A \rVert = \lvert a \rvert \cdot \lVert A \rVert,对任意的a \in R ∥aA∥=∣a∣⋅∥A∥,对任意的a∈R
- 三角不等式: ∥ A + B ∥ ≤ ∥ A ∥ + ∥ B ∥ \lVert A + B \rVert \leq \lVert A \rVert + \lVert B \rVert ∥A+B∥≤∥A∥+∥B∥
- 相容性: ∥ A B ∥ ≤ ∥ A ∥ ∥ B ∥ \lVert A B \rVert \leq \lVert A \rVert \lVert B \rVert ∥AB∥≤∥A∥∥B∥ 则称 ∥ ⋅ ∥ 是一个矩阵范数 则称\lVert \cdot \rVert 是一个矩阵范数 则称∥⋅∥是一个矩阵范数
函数范数的数学定义
在连续函数空间
C
[
a
,
b
]
中范数的定义为:
在连续函数空间C[a, b]中范数的定义为:
在连续函数空间C[a,b]中范数的定义为:
在函数空间
C
[
a
,
b
]
中,
f
∈
C
[
a
,
b
]
,若存在唯一实数
∥
⋅
∥
满足:
在函数空间C[a, b] 中, f \in C[a, b],若存在唯一实数\lVert \cdot \rVert 满足:
在函数空间C[a,b]中,f∈C[a,b],若存在唯一实数∥⋅∥满足:
- 正定性: ∥ f ∥ ≥ 0 ,当且仅当 f = 0 时, ∥ f ∥ = 0 \lVert f \rVert \geq 0,当且仅当 f = 0时,\lVert f \rVert = 0 ∥f∥≥0,当且仅当f=0时,∥f∥=0
- 其次性: ∀ a ∈ R , ∥ a f ∥ = ∣ a ∣ ⋅ ∥ f ∥ \forall a \in R, \lVert a f \rVert = \lvert a \rvert \cdot \lVert f \rVert ∀a∈R,∥af∥=∣a∣⋅∥f∥
- 三角不等式: ∥ f + g ∥ ≤ ∥ f ∥ ⋅ ∥ g ∥ , f , g ∈ C [ a , b ] \lVert f + g \rVert \leq \lVert f \rVert \cdot \lVert g \rVert,f,g \in C[a, b] ∥f+g∥≤∥f∥⋅∥g∥,f,g∈C[a,b]
常见的函数范数:
函数的 ∞ − 范数: ∥ f ∥ ∞ = max a < x < b ∣ f ( x ) ∣ 函数的\infty - 范数:\lVert f \rVert_\infty = \operatorname*{max}_{a < x <b}{\lvert f(x) \rvert} 函数的∞−范数:∥f∥∞=a<x<bmax∣f(x)∣函数的 1 − 范数: ∥ f ∥ 1 = ∫ a b ∣ f ( x ) ∣ d x 函数的1 - 范数: \lVert f \rVert_1 = \int_{a}^{b}{\lvert f(x) \rvert \,{\rm d}x} 函数的1−范数:∥f∥1=∫ab∣f(x)∣dx函数的 2 − 范数: ∥ f ∥ 2 = ∣ ∫ a b f 2 ( x ) d x ∣ 1 2 函数的2 - 范数:\lVert f \rVert_2 = \lvert \int_{a}^{b}{ f^2(x) \,{\rm d}x} \rvert^{\frac{1}{2}} 函数的2−范数:∥f∥2=∣∫abf2(x)dx∣21
例子:
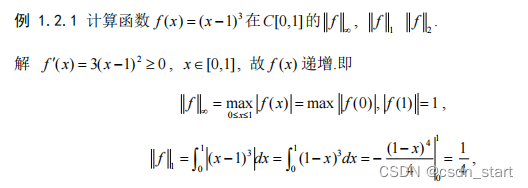
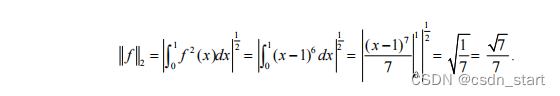
本文转载自: https://blog.csdn.net/csdn_start/article/details/129678301
版权归原作者 csdn_start 所有, 如有侵权,请联系我们删除。
版权归原作者 csdn_start 所有, 如有侵权,请联系我们删除。