[详解栈和队列]数据结构之栈与队列

✅作者简介：大家好,我是Philosophy7？让我们一起共同进步吧！🏆 📃个人主页：Philosophy7的csdn博客
🔥系列专栏： 👑哲学语录: 承认自己的无知，乃是开启智慧的大门
💖如果觉得博主的文章还不错的话，请点赞👍+收藏⭐️+留言📝支持一下博>主哦🤞

文章目录

栈和队列

1.物理结构和逻辑结构

再了解栈和队列之前，我们要先知道什么是逻辑结构和物理结构。

逻辑结构:

按照逻辑结构划分:数据结构可分为线性结构和非线性接口

线性结构就包括:顺序表、栈、队列

非线性结构:树、图

物理结构:

按照物理结构划分:数据结构可分为顺序存储结构、链式存储结构

顺序存储结构我们常见的就有:数组

链式存储结构:链表

举个栗子:

比如说人的精神、思想是看不见的摸不着的，为什么你能感受到他的一个精神和思想呢，肯定是通过你所能看得见的。

就比如说通过他这个人的言行举止，你就可以发现这个人确实是大佬。

所以逻辑结构是抽象的概念，它依赖于物理结构而存在。

下面我们就来介绍栈和队列，这两种是属于逻辑结构的，它们的物理结构依赖于数组或链表。

2.什么是栈

大家打过

手枪

的都知道，手枪的弹匣就是一种栈的结构,是一种

先进后出

的一种结构，例如:最先装进弹匣里的子弹是最后才能打出来的，而最后一颗装进弹匣里的是最先打出来的。

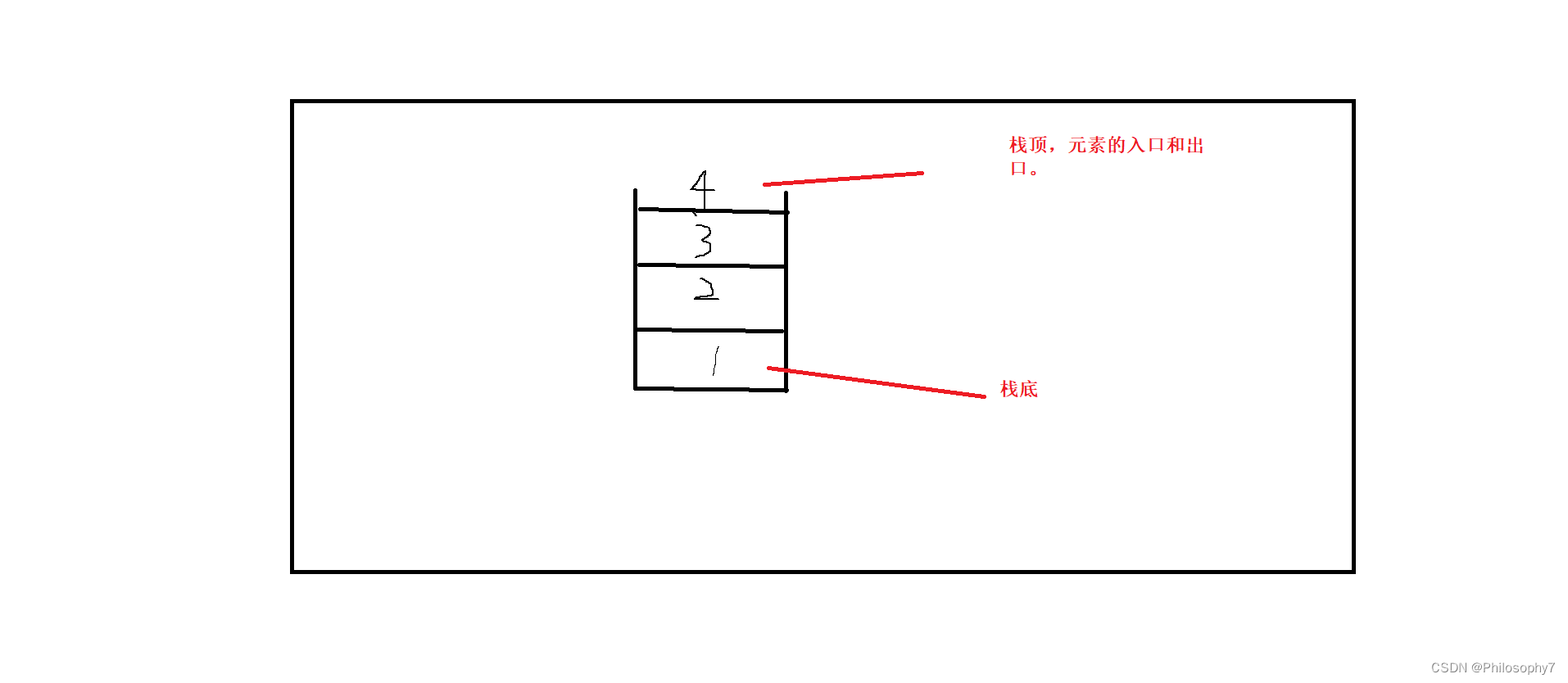
所以栈是一种线性的数据结构，栈中的元素只能

先进后出

。最早进入的元素存放的叫做

栈底

，最后进入元素存放的位置叫作

栈顶

。

2.1栈的基本操作

1. 入栈 - 入栈的操作就是把新元素放入栈中，只允许从栈顶一侧放入元素，新元素的位置将会成为新的栈顶。
2. 出栈 - 出栈就是将元素从栈顶弹出，弹出之后，栈顶自然是原先栈顶元素的前一个元素了。

这里我们基于数组的方式实现

packagecom.philosophy7.stack;/*
    基于数组实现栈
 *//**
 * @author Philosophy7
 */publicclassMyStack{publicstaticvoidmain(String[] args){MyStack myStack =newMyStack(5);
        myStack.push(5);
        myStack.push(4);
        myStack.push(3);System.out.println("出来的元素是:"+ myStack.pop());
        myStack.list();}privateint size;//栈的大小privateint[] stack;//数组充当栈privateint top =-1;//栈顶 初始化-1 数组的索引是从0开始 入栈操作是从栈顶往下放入元素publicMyStack(int size){this.size = size;
        stack =newint[size];}//首先判断栈是否还能存储publicbooleanisFull(){return top == size -1;}//栈空publicbooleanisEmpty(){return top ==-1;}//入栈publicvoidpush(int element){//1.首先判断栈是否满了if(isFull()){System.out.println("满了哦");return;}//2.否则将数据插入
        top++;
        stack[top]= element;}//出栈publicIntegerpop(){int value;//1.首先判断栈是否有元素可出if(isEmpty()){System.out.println("栈空了 出个屁啊");returnnull;}
        value = stack[top];
        top--;return value;}//遍历栈 从栈顶往栈底遍历publicvoidlist(){if(isEmpty()){System.out.println("栈空了 出个屁啊");return;}for(int i = top; i >=0; i--){System.out.println(stack[i]);}}}

3.什么是队列

就比如说这张排队买火车票的示例来说，最先排队的人最先买到票，买到票也就可以直接

提桶跑路

了，也就不需要继续等待了，后面的人要想买到票只能等待前面的人买完了才能轮到他自己，否则的话是要一直等待下去的。有的小伙伴看到这里就会想，我可以插队啊！！在这里我只想说小伙子路还长，大好青春可不能就此结束啊！！

所以队列也属于逻辑结构，是一种线性数据结构，它的特征当然是

先进先出

啦，队列的出口端叫作

队头

，队列的入口端叫作

队尾

队列的基本操作

1. 入队 - 入队就是将新元素放入队列中，只允许在队尾的位置放入元素，新元素的下一个位置将会成为队尾。
2. 出队 - 出队操作就是把元素移除队列，只允许在队头的一端移出元素，出队元素的后一个元素将会成为新的队头。

packagecom.philosophy7.queue;/**
 * @author Philosophy7
 */publicclassMyQueue{publicstaticvoidmain(String[] args){MyQueue myQueue =newMyQueue(5);
        myQueue.enQueue(1);
        myQueue.enQueue(2);
        myQueue.enQueue(3);System.out.println("出队的元素是:"+ myQueue.deQueue());

        myQueue.list();}privateint[] queue;//基于数组充当队列privateint front;//队头privateint rear;//队尾 元素的入口privateint count;//计数器//判断队列是否满publicbooleanisFull(){if(count >0& front == rear){returntrue;}else{returnfalse;}}//判断栈是否为空publicbooleanisEmpty(){if(count ==0){returntrue;}else{returnfalse;}}//返回队列容量publicintsize(){return queue.length;}publicMyQueue(int capacity){this.queue =newint[capacity];}//入队publicvoidenQueue(int element){//1.判断队列是否还能容纳元素if(isFull()){System.out.println("排队的人太多了 容纳不下了");return;}//2.入队操作
        queue[rear]= element;
        rear++;if(rear == queue.length)rear=0;//队尾＝队列中的容纳数后 将队尾设置为0
        count++;}//出队publicintdeQueue(){int value =0;if(isEmpty()){System.out.println("队列中没有元素");return0;}//2.出队操作
        value = queue[front];
        front++;if(front == queue.length)front=0;
        count--;return value;}//遍历队列publicvoidlist(){if(isEmpty()){return;}for(int i =0; i < queue.length; i++){System.out.println(queue[i]);}}}

小结

数据结构能够按照逻辑结构和物理结构划分

逻辑结构:线性结构和非线性结构

物理结构:顺序存储和链式存储结构

栈: 一种先入后出的数据结构，最早进入栈中的元素为栈底，最后进入栈中的元素为栈顶

队列:一种先入先出的数据结构，队列的出口叫作队头，队列的入口叫做队尾。

栈的移动只会影响到最后一个元素，不会整体的移动元素。

队列的移动同样也不会影响到整体元素，所以不管是数组还是链表它们的入栈出栈 入队出队操作的时间复杂度是

O(1)

点赞👍+关注💖+收藏⭐