前言
聚类算法中的层次聚类方法是一种已得到广泛使用的经典方法,是通过将数据对象组织成若干组并形成一个相应的树来进行聚类。Birch算法就是一种基于层次聚类的方法,所以我们在本文介绍一下Birch算法
一、Birch算法基本思想
BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies)全称是:利用层次方法的平衡迭代规约和聚类。定义很长,但是其实只要明白它是用一棵树来聚类和规约数据就可以了
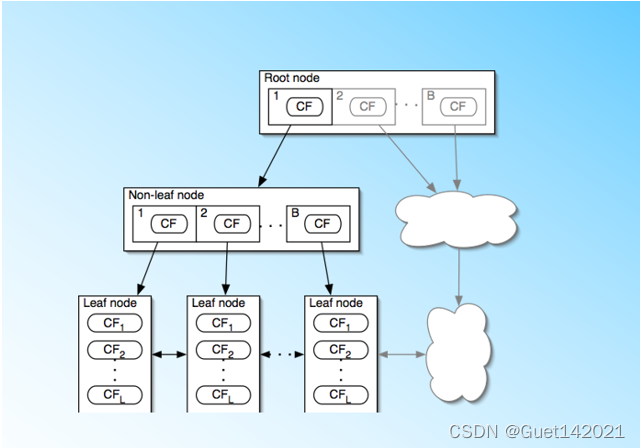
先让我们看看CF tree长什么样,如上图所示, BIRCH算法利用了一个树结构来帮助我们快速的聚类,这个数结构类似于平衡B+树,一般将它称之为聚类特征树(Clustering Feature Tree,简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature,简称CF)组成。从左图我们可以看看聚类特征树是什么样子的:每个节点包括叶子节点都有若干个CF,而内部节点的CF有指向孩子节点的指针,所有的叶子节点用一个双向链表链接起来。
二、聚类特征CF和CF 树
1.聚类特征CF
如果某个簇包含N个d维的数据对象{o1,o2,…,oN},则聚类特征定义为一个三元组CF=(N,LS,SS)。其中LS是N个对象的线性和,SS是N个对象的平方和,即:
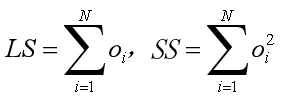
聚类特征概括了对象簇的信息,在BIRCH算法中做聚类决策所需要的度量值,如簇的质心、半径、直径、簇间质心距离和平均簇间距离等都可以通过聚类特征CF计算出来。
质心计算公式:
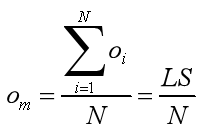
半径计算公式:
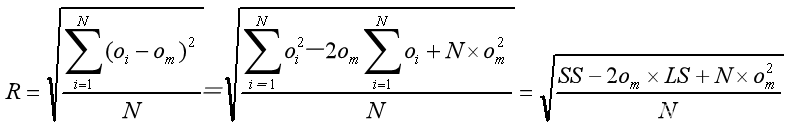
所以我们可以看到,其实聚类特征是包含了这个簇的很多信息,但是它却不需要全部存储下来,只需要一个简单的三元组就可以囊括了这个簇的所有信息,使得内存占用空间大大减少。
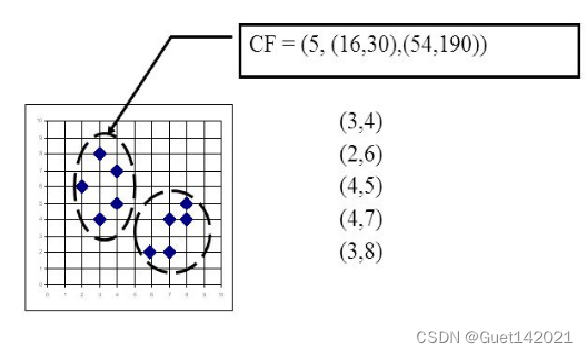
举个例子如图,在CF Tree中的某一个节点的某一个CF中,有下面5个样本(3,4), (2,6), (4,5), (4,7), (3,8)。则它对应的N=5, LS=(3+2+4+4+3,4+6+5+7+8)=(16,30), SS=(3²+2²+4²+4²+3²+4²+6²+5²+7²+8²)=(54+190)=244
2.CF tree
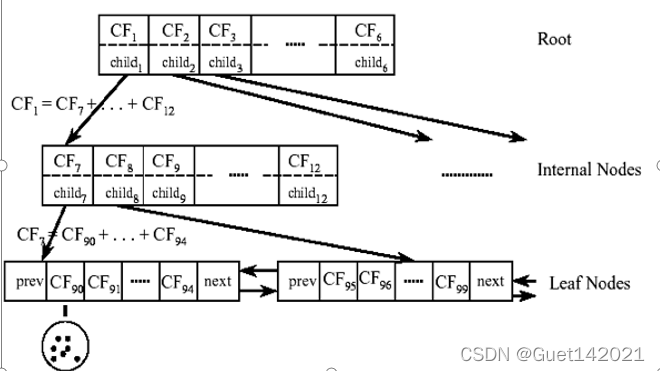
CF有一个很好的性质,就是满足线性关系,也就是CF1+CF2=(N1+N2,LS1+LS2,SS1+SS2)。这个性质从定义也很好理解。如果把这个性质放在CF Tree上,也就是说,在CF Tree中,对于每个父节点中的CF节点,它的(N,LS,SS)三元组的值等于这个CF节点所指向的所有子节点的三元组之和。
从上图中可以看出,根节点的CF1的三元组的值,可以从它指向的6个子节点(CF7 - CF12)的值相加得到。这样我们在更新CF Tree的时候,只需要进行简单的加减操作,可以很高效的进行聚类。
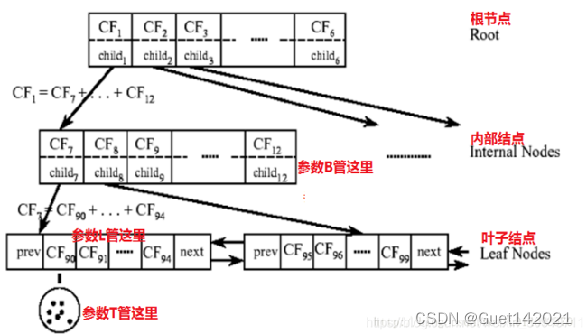
CF tree可以分为根节点,内部节点,叶子节点3大类,其中每个节点都是有多个CF构成的。对于一颗CF tree, 有以下3个重要参数
内部节点的最大CF数目,称之为枝平衡因子B
叶子节点的最大CF数目,称之为叶平衡因子L
叶子节点的空间阈值T,计算样本点与CF的空间距离,如果小于阈值,则将样本纳入某个CF
3.CF tree 的生成
以下内容来自刘建平Pinard-博客园的学习笔记,总结如下:
我们先定义好CF Tree的参数: 即内部节点的最大CF数B=3, 叶子节点的最大CF数L=3, 叶节点每个CF的最大样本半径阈值T。 在最开始的时候,CF Tree是空的,没有任何样本,我们从训练集读入第一个样本点,将它放入一个新的CF三元组A,这个三元组的N=1,将这个新的CF放入根节点,此时的CF Tree如图:
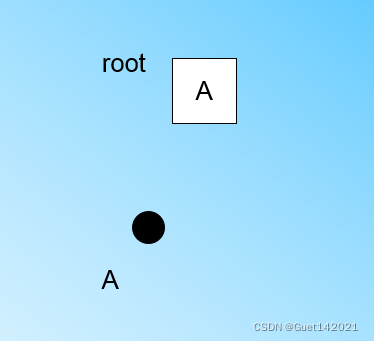
现在我们继续读入第二个样本点,我们发现这个样本点和第一个样本点A,在半径为T的超球体范围内,也就是说,他们属于一个CF,我们将第二个点也加入CF A,此时需要更新A的三元组的值。此时A的三元组中N=2。此时的CF Tree如图:
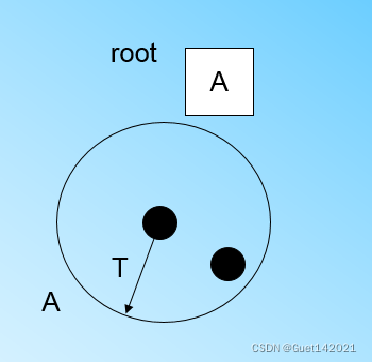
此时来了第三个节点,结果我们发现这个节点不能融入刚才前面的节点形成的超球体内,也就是说,我们需要一个新的CF三元组B,来容纳这个新的值。此时根节点有两个CF三元组A和B,此时的CF Tree如图:
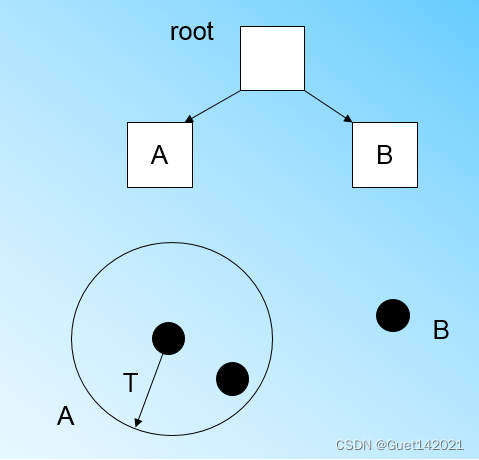
假设我们现在的CF Tree 如图, 叶子节点LN1有三个CF, LN2和LN3各有两个CF。我们的叶子节点的最大CF数L=3。此时一个新的样本点来了,我们发现它离LN1节点最近,因此开始判断它是否在sc1,sc2,sc3这3个CF对应的超球体之内,但是很不幸,它不在,因此它需要建立一个新的CF,即sc8来容纳它。问题是我们的L=3,也就是说LN1的CF个数已经达到最大值了,不能再创建新的CF了,怎么办?此时就要将LN1叶子节点一分为二了。
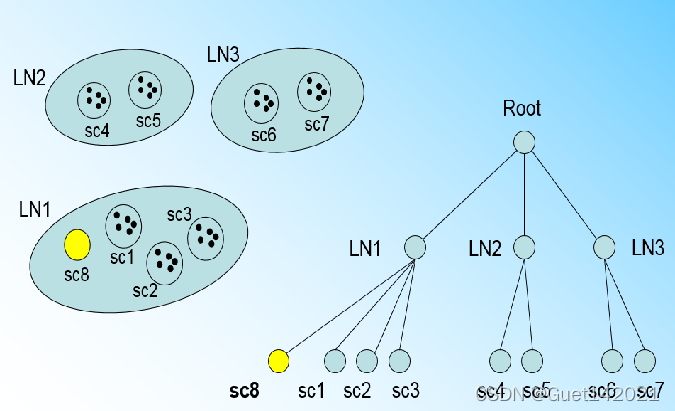
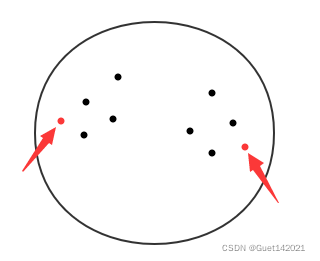
具体怎么分,如图所示,我们在CF元组中的所有数据中,找到最远的两个点作为种子节点(如图中红点),然后根据距离把剩下的点划分到两个节点中,形成两个簇。
回到之前的图,我们将LN1里所有CF元组中,找到两个最远的CF做这两个新叶子节点的种子CF,然后将LN1节点里所有CF sc1, sc2, sc3,以及新样本点的新元组sc8划分到两个新的叶子节点上。将LN1节点划分后的CF Tree如下图
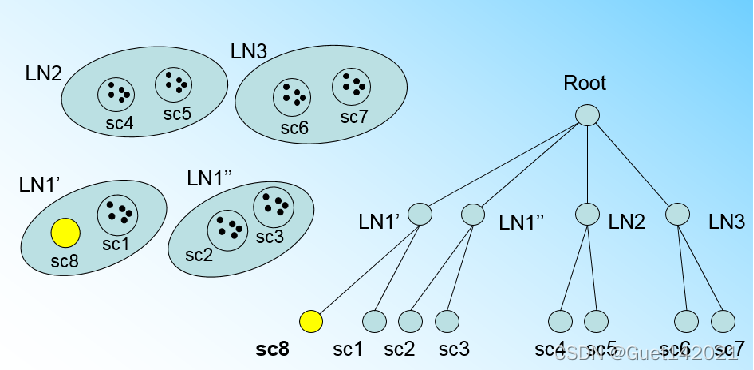
更新完叶子结点,返回上一层,检查父节点是否需要分裂,如果需要,按照叶子结点分裂方法进行分裂,一直检查到根节点。
因为我们的内部节点的最大CF数B=3,则此时叶子节点一分为二会导致根节点的最大CF数超了,也就是说,我们的根节点现在也要分裂,分裂的方法和叶子节点分裂一样,最后分裂后的CF Tree如下图:
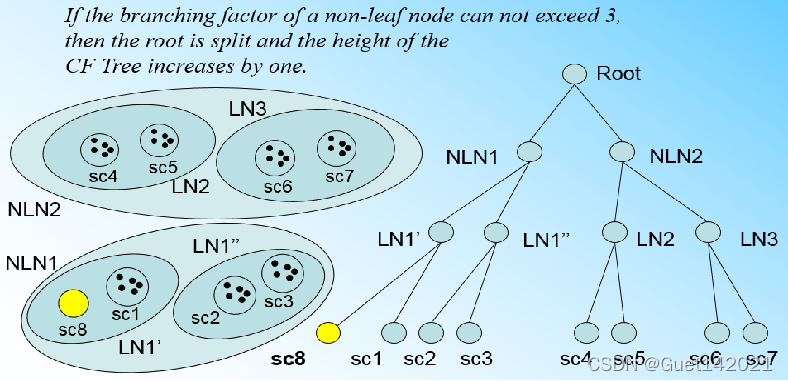
总结下CF Tree的插入:
从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的CF节点
到达叶子结点后,检查最近的CF节点能否吸收
是,这个CF节点对应的超球体半径仍然满足小于阈值T,则更新路径上所有的CF三元组 否,如果当前叶子节点的CF节点个数小于阈值L,是否可以添加一个新的CF节点 是,放入新样本,将新的CF节点放入这个叶子节点,更新路径上所有的CF三元组 否,分裂当前叶子结点中距离最远的两个CF元组,作为种子,按最近距离重新分配
3.更新每个非叶节点的CF信息,依次向上检查父节点是否也要分裂,如果需要按和叶子节点分裂方式相同。
三、Birch算法流程
1.birch算法的优化
上面扯了半天CF tree,那我们的Birch算法到底是啥呢?接下来我们言归正传,说一下Birch算法的算法流程。首先,既然算法是根据一棵树来进行聚类,那么显然我们可以通过优化这棵树来提升聚类效果,话不多说,直接上图。
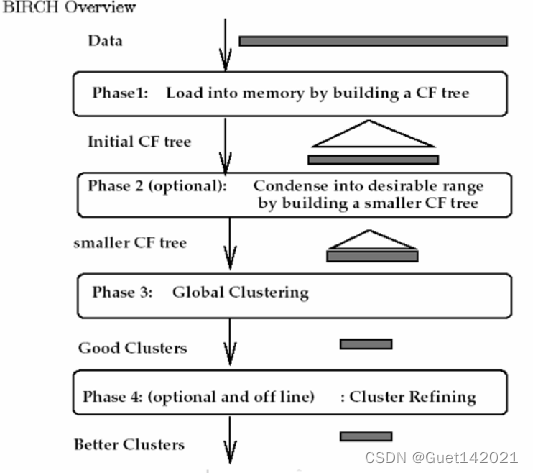
现在我们就来看看 BIRCH算法的流程。
1) 将所有的样本依次读入,在内存中建立一颗CF Tree, 建立的方法参考上一节。
2)(可选)将第一步建立的CF Tree进行筛选,去除一些异常CF节点,这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并
3)(可选)利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类,得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构,以及一些由于节点CF个数限制导致的树结构分裂。
4)(可选)利用第三步生成的CF Tree的所有CF节点的质心,作为初始质心点,对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。
从上面可以看出,BIRCH算法的关键就是步骤1,也就是CF Tree的生成,其他步骤都是为了优化最后的聚类结果。所以我们前面只要搞懂这棵树怎么来的,birch算法的思想你就掌握啦
2.算法优缺点
BIRCH算法的主要优点有:
1、节省内存。叶子节点放在磁盘分区上,非叶子节点仅仅是存储了一个CF值,外加指向父节点和孩子节点的指针。
2、快。计算两个簇的距离只需要用到(N,LS,SS)这三个值足矣。
3、只需扫描一遍数据集即可建树,即一个数据集就是一棵树。
4、可识别噪声点。建立好CF树后把那些包含数据点少的子簇剔除。
缺点:
1、对非球状的簇聚类效果不好。这取决于簇直径和簇间距离的计算方法。
2、对高维数据聚类效果不好。
3、由于每个节点只能包含一定数目的子节点,最后得出来的簇可能和自然簇相差很大。
4、整个过程中算法一旦中断,一切必须从头再来。
四、算法实验实例
实验数据:scikit中的make_blobs方法常被用来生成聚类算法的测试数据,make_blobs可以根据用户指定的特征数量、样本数量、类别数、每个类别的方差等来生成几类数据,这些数据可用于测试聚类算法的效果。本实验的设置是生成5000个样本,每个样本有2个特征,共生成5个簇,簇中心分别在[-1,-1], [0,0], [1,1],[1,-1],[-1,1],每个簇的方差分别为0.4, 0.3, 0.4, 0.3,0.4。样本示意图如图所示
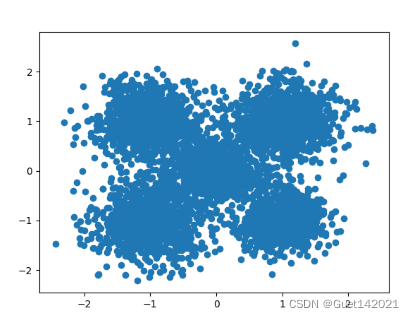
评价指标:本实验使用Davies-Bouldin指数(DBI)进行算法性能评测,该指标的原理是计算所有簇的类内距离和类间距离的比值(类内/类间),比值越小越好。即希望类间距离越大、类内距离越小(数据越集中)越好。
1、研究不指定簇数的情况下,Birch算法的聚类情况
设置CF最大样本半径阈值为0.5,CF Tree各个节点最大CF数为50。不指定簇数的情况下,Birch算法的聚类情况如图所示,样本一共被分为了10簇,DB指数为1.015。此时的簇数即为所有叶子节点的CF个数,也就是说叶子节点有多少CF,Birch算法就默认将样本分为多少簇。
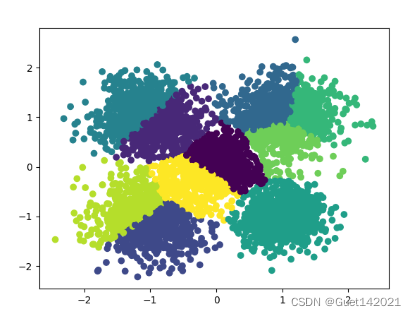
2、研究聚类簇数对Birch算法的影响
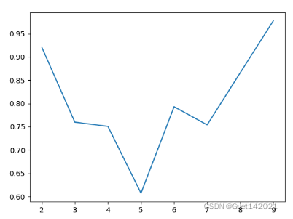
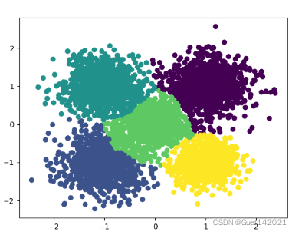
设置CF最大样本半径阈值为0.5,CF Tree各个节点最大CF数为50。Birch算法的DB指数随聚类簇数变化示意图如下左图所示。由图可知在簇数为5时DB指数最低,设置簇数为5的情况下,DB指数为0.6072。
Birch算法的聚类情况如下右图所示。相对于不指定簇数的情况下DB指数降低了,这是由于我们通过make_blobs方法生成了5簇数据,Birch算法在不指定簇数的情况下可能不能正确聚类,当然这也跟节点内最大CF个数以及每个CF的最大样本半径阈值的设置相关。
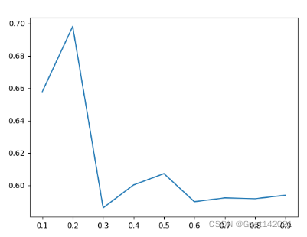
3、研究CF半径阈值对Birch算法的影响
设置聚类簇数为5,CF Tree各个节点最大CF数为50。Birch算法的DB指数随CF半径阈值的变化示意图如下左图所示。
由图可知在CF半径阈值为0.3时DB指数最低,此时DB指数为0.5861,Birch算法的聚类情况如下右图所示。
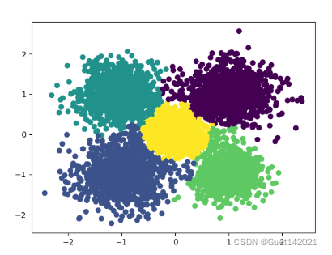
4、研究每个节点内最大CF个数对Birch算法的影响
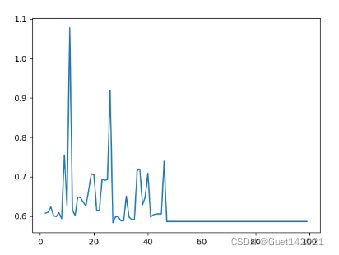
设置聚类簇数为5,CF半径阈值为0.3。Birch算法的DB指数随节点内最大CF个数的变化示意图如下左图所示。
由图可知在最大CF个数为27时DB指数最低,此时DB指数为0.5828,Birch算法的聚类情况如下右图所示。
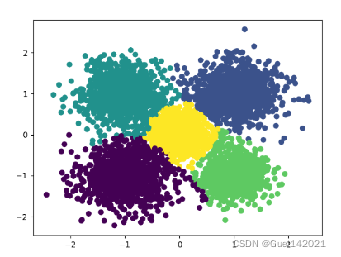
实验总结
根据上述一系列实验可知,Birch算法聚类结果的好坏与聚类簇数、节点内最大CF个数、CF内最大半径阈值这三个因素直接相关。合理设置参数才能将Birch算法模型性能调至最优。
参考文献
刘建平Pinard
版权归原作者 Guet142021 所有, 如有侵权,请联系我们删除。