前两篇文章我们已经介绍了自回归模型PixelCNNs,以及如何处理多维输入数据,本篇文章我们将关注 PixelCNNs 的最大限制之一(即盲点)以及如何改进以修复它。
在前两篇文章中,我们介绍了生成模型PixelCNN 概念并研究了彩色 PixelCNN 的工作原理。PixelCNN 是一种学习像素概率分布的生成模型,未来像素的强度将由之前的像素决定。在以前的文章中,我们实现了两个 PixelCNN,并注意到性能并不出色。我们也提到提高模型性能的方法之一是修复盲点问题。在这篇文章中我们将介绍盲点的概念,讨论 PixelCNN 是如何受到影响的,并实现一种解决方案——Gated PixelCNN。
盲点
PixelCNN 学习图像中所有像素的条件分布并使用此信息进行预测。PixelCNN 将学习像素从左到右和从上到下的分布,通常使用掩码来确保“未来”像素(即正在预测的像素右侧或下方的像素)不能用于给定像素的预测。如下图A所示,掩码将当前被预测的像素(这对应于掩码中心的像素)“之后”的像素清零。但是这种操作导致并不是所有“过去”的像素都会被用来计算新点,丢失的信息会产生盲点。

要了解盲点问题,让我们看上图B。在图B 中,深粉色点 (m) 是我们要预测的像素,因为它位于过滤器的中心。如果我们使用的是 3x3 掩码 (上图A.),像素 m 取决于 l、g、h、i。另一方面,这些像素取决于之前的像素。例如,像素g依赖于f、a、b、c,像素i依赖于h、c、d、e。从上图 B 中,我们还可以看到,尽管出现在像素 m 之前,但从未考虑像素 j 来计算 m 的预测。同样,如果我们想对 q、j、n、o 进行预测,则永远不会考虑(上图C橙色部分)。所以并非所有先前的像素都会影响预测,这种情况就被称为盲点问题。
我们将首先看看pixelcnn的实现,以及盲点将如何影响结果。下面的代码片段展示了使用Tensorflow 2.0的PixelCNN实现掩码。
class MaskedConv2D(keras.layers.Layer):
"""Convolutional layers with masks.
Convolutional layers with simple implementation of masks type A and B for
autoregressive models.
Arguments:
mask_type: one of `"A"` or `"B".`
filters: Integer, the dimensionality of the output space
(i.e. the number of output filters in the convolution).
kernel_size: An integer or tuple/list of 2 integers, specifying the
height and width of the 2D convolution window.
Can be a single integer to specify the same value for
all spatial dimensions.
strides: An integer or tuple/list of 2 integers,
specifying the strides of the convolution along the height and width.
Can be a single integer to specify the same value for
all spatial dimensions.
Specifying any stride value != 1 is incompatible with specifying
any `dilation_rate` value != 1.
padding: one of `"valid"` or `"same"` (case-insensitive).
kernel_initializer: Initializer for the `kernel` weights matrix.
bias_initializer: Initializer for the bias vector.
"""
def __init__(self,
mask_type,
filters,
kernel_size,
strides=1,
padding='same',
kernel_initializer='glorot_uniform',
bias_initializer='zeros'):
super(MaskedConv2D, self).__init__()
assert mask_type in {'A', 'B'}
self.mask_type = mask_type
self.filters = filters
self.kernel_size = kernel_size
self.strides = strides
self.padding = padding.upper()
self.kernel_initializer = initializers.get(kernel_initializer)
self.bias_initializer = initializers.get(bias_initializer)
def build(self, input_shape):
self.kernel = self.add_weight('kernel',
shape=(self.kernel_size,
self.kernel_size,
int(input_shape[-1]),
self.filters),
initializer=self.kernel_initializer,
trainable=True)
self.bias = self.add_weight('bias',
shape=(self.filters,),
initializer=self.bias_initializer,
trainable=True)
center = self.kernel_size // 2
mask = np.ones(self.kernel.shape, dtype=np.float64)
mask[center, center + (self.mask_type == 'B'):, :, :] = 0.
mask[center + 1:, :, :, :] = 0.
self.mask = tf.constant(mask, dtype=tf.float64, name='mask')
def call(self, input):
masked_kernel = tf.math.multiply(self.mask, self.kernel)
x = nn.conv2d(input,
masked_kernel,
strides=[1, self.strides, self.strides, 1],
padding=self.padding)
x = nn.bias_add(x, self.bias)
return x
观察原始PixelCNN的接收域(下图2中用黄色标记),我们可以看到盲点以及它是如何在不同层上传播的。在这本篇文章的第二部分,我们将使用改进版的PixelCNN,门控PixelCNN,它引入了一种新的机制来避免盲点的产生。

图2:PixelCNN上盲点区域的可视化
Gated PixelCNN
为了解决这些问题,van den Oord等人(2016)引入了门控PixelCNN。门控PixelCNN不同于PixelCNN在两个主要方面:
- 它解决了盲点问题
- 使用门控卷积层提高了模型的性能
Gated PixelCNN 如何解决盲点问题
这个新模型通过将卷积分成两部分来解决盲点问题:垂直和水平堆栈。让我们看看垂直和水平堆栈是如何工作的。

图 3:垂直(绿色)和水平堆栈(蓝色 )
在垂直堆栈中,目标是处理当前行之前所有行的上下文信息。用于确保使用所有先前信息并保持因果关系(当前预测的像素不应该知道其右侧的信息)的方法是分别将掩码的中心向上移动到被预测的像素上一行。如图3所示,中心是浅绿色的像素(m),但垂直堆栈收集的信息不会用于预测它,而是用于预测它下面一行的像素(r)。
单独使用垂直堆栈会在黑色预测像素 (m) 的左侧产生盲点。为避免这种情况,垂直堆栈收集的信息与来自水平堆栈的信息(图 3 中以蓝色表示的 p-q)相结合,从而预测需要预测的像素 (m) 左侧的所有像素。水平和垂直堆栈的结合解决了两个问题:
(1)不会使用预测像素右侧的信息,
(2)因为我们作为一个块来考虑,不再有盲点。
原始论文通过感受野具有 2x3的卷积实现了垂直堆栈 。在本篇文章中我们则通过使用 3x3 卷积并屏蔽掉最后一行来实现这一点。在水平堆栈中,卷积层将预测值与来自当前分析像素行的数据相关联。这可以使用 1x3 卷积来实现,这样就可以屏蔽未来的像素以保证自回归模型的因果关系条件。与 PixelCNN 类似,我们实现了 A 型掩码(用于第一层)和 B 型掩码(用于后续层)。
下面的代码片段展示了使用 Tensorflow 2.0 框架实现的掩码。
class MaskedConv2D(keras.layers.Layer):
"""Convolutional layers with masks.
Convolutional layers with simple implementation of masks type A and B for
autoregressive models.
Arguments:
mask_type: one of `"A"` or `"B".`
filters: Integer, the dimensionality of the output space
(i.e. the number of output filters in the convolution).
kernel_size: An integer or tuple/list of 2 integers, specifying the
height and width of the 2D convolution window.
Can be a single integer to specify the same value for
all spatial dimensions.
strides: An integer or tuple/list of 2 integers,
specifying the strides of the convolution along the height and width.
Can be a single integer to specify the same value for
all spatial dimensions.
Specifying any stride value != 1 is incompatible with specifying
any `dilation_rate` value != 1.
padding: one of `"valid"` or `"same"` (case-insensitive).
kernel_initializer: Initializer for the `kernel` weights matrix.
bias_initializer: Initializer for the bias vector.
"""
def __init__(self,
mask_type,
filters,
kernel_size,
strides=1,
padding='same',
kernel_initializer='glorot_uniform',
bias_initializer='zeros'):
super(MaskedConv2D, self).__init__()
assert mask_type in {'A', 'B', 'V'}
self.mask_type = mask_type
self.filters = filters
self.kernel_size = kernel_size
self.strides = strides
self.padding = padding.upper()
self.kernel_initializer = initializers.get(kernel_initializer)
self.bias_initializer = initializers.get(bias_initializer)
def build(self, input_shape):
kernel_h = self.kernel_size
kernel_w = self.kernel_size
self.kernel = self.add_weight('kernel',
shape=(self.kernel_size,
self.kernel_size,
int(input_shape[-1]),
self.filters),
initializer=self.kernel_initializer,
trainable=True)
self.bias = self.add_weight('bias',
shape=(self.filters,),
initializer=self.bias_initializer,
trainable=True)
mask = np.ones(self.kernel.shape, dtype=np.float64)
# Get centre of the filter for even or odd dimensions
if kernel_h % 2 != 0:
center_h = kernel_h // 2
else:
center_h = (kernel_h - 1) // 2
if kernel_w % 2 != 0:
center_w = kernel_w // 2
else:
center_w = (kernel_w - 1) // 2
if self.mask_type == 'V':
mask[center_h + 1:, :, :, :] = 0.
else:
mask[:center_h, :, :] = 0.
mask[center_h, center_w + (self.mask_type == 'B'):, :, :] = 0.
mask[center_h + 1:, :, :] = 0.
self.mask = tf.constant(mask, dtype=tf.float64, name='mask')
def call(self, input):
masked_kernel = tf.math.multiply(self.mask, self.kernel)
x = nn.conv2d(input,
masked_kernel,
strides=[1, self.strides, self.strides, 1],
padding=self.padding)
x = nn.bias_add(x, self.bias)
return x
通过在整个网络中添加这两个堆栈的特征图,我们得到了一个具有一致感受野且不会产生盲点的自回归模型(图 4)。

图 4:Gated PixelCNN 的感受野可视化。我们注意到,使用垂直和水平堆栈的组合,我们能够避免在 PixelCNN 的初始版本中观察到的盲点问题(对比图2)。
门控激活单元(或门控块)
从原始的PixelCNNs 到 Gated CNNs 的第二个主要改进是引入了门控块和乘法单元(以 LSTM 门的形式)。因此,而不是像原始PixelCNNs 那样在掩码卷积之间使用ReLU;Gated PixelCNN 使用门控激活单元来模拟特征之间更复杂的交互。这个门控激活单元使用 sigmoid(作为遗忘门)和 tanh(作为真正的激活)。在原始论文中,作者认为这可能是 PixelRNN(使用 LSTM 的)优于 PixelCNN 的原因之一,因为它们能够通过循环更好地捕获过去的像素——它们可以记住过去的信息。因此,Gated PixelCNN 添加并使用了以下内容:
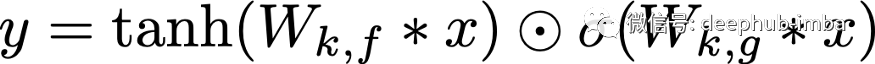
σ 是 sigmoid ,k 是层数,⊙ 是元素乘积,* 是卷积算子,W 是来自前一层的权重。有了这个公式我们就可以更详细地介绍 PixelCNN 中的单个层。
Gated PixelCNN 中的单层块
堆栈和门是 Gated PixelCNN 的基本块(下图 5)。但是它们是如何连接的,信息将如何处理?我们将把它分解成 4 个处理步骤,我们将在下面的会话中讨论。
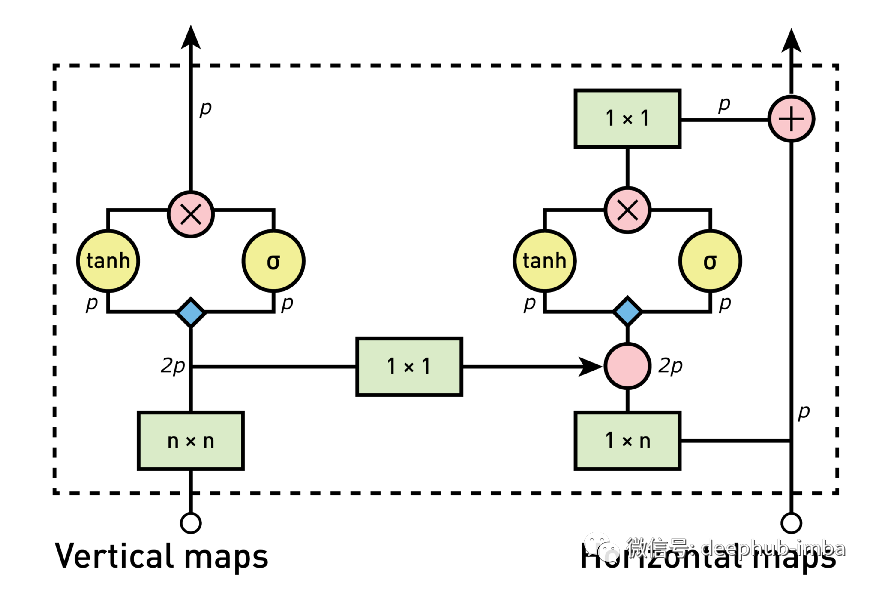
图 5:Gated PixelCNN 架构概述(来自原始论文的图像)。颜色代表不同的操作(即,绿色:卷积;红色:元素乘法和加法;蓝色:具有权重的卷积
1、计算垂直堆栈特征图

作为第一步,来自垂直堆栈的输入由3x3 卷积层和垂直掩码处理。然后生成的特征图通过门控激活单元并输入到下一个块的垂直堆栈中。
2、将垂直地图送入水平堆栈

对于自回归模型,需要结合垂直和水平堆栈的信息。为此在每个块中垂直堆栈也用作水平层的输入之一。由于垂直堆栈的每个卷积步骤的中心对应于分析的像素,所以我们不能只添加垂直信息,这将打破自回归模型的因果关系条件,因为它将允许使用未来像素的信息来预测水平堆栈中的值。下图 8A 中的第二幅图就是这种情况,其中黑色像素右侧(或未来)的像素用于预测它。因为这个原因在将垂直信息提供给水平堆栈之前,需要使用填充和裁剪将其向下移动(图 8B)。通过对图像进行零填充并裁剪图像底部,可以确保垂直和水平堆栈之间的因果关系。我们将在以后的文章中深入研究裁剪如何工作的更多细节,所以如果它的细节不完全清楚,请不要担心

图8:如何保证像素之间的因果关系
3、计算水平特征图

在这一步中,处理水平卷积层的特征图。事实上,首先从垂直卷积层到水平卷积层输出的特征映射求和。这种组合的输出具有理想的接收格式,它考虑了所有以前像素的信息,然后就是通过门控激活单元。
4、计算水平叠加上的残差连接

在这最后一步中,如果该块不是网络的第一个块,则使用残差连接合并上一步的输出(经过1x1卷积处理),然后送入下一个块的水平堆栈。如果是网络的第一个块,则跳过这一步。
使用Tensorflow 2的代码如下:
class GatedBlock(tf.keras.Model):
""" Gated block that compose Gated PixelCNN."""
def __init__(self, mask_type, filters, kernel_size):
super(GatedBlock, self).__init__(name='')
self.mask_type = mask_type
self.vertical_conv = MaskedConv2D(mask_type='V',
filters=2 * filters,
kernel_size=kernel_size)
self.horizontal_conv = MaskedConv2D(mask_type=mask_type,
filters=2 * filters,
kernel_size=kernel_size)
self.padding = keras.layers.ZeroPadding2D(padding=((1, 0), 0))
self.cropping = keras.layers.Cropping2D(cropping=((0, 1), 0))
self.v_to_h_conv = keras.layers.Conv2D(filters=2 * filters, kernel_size=1)
self.horizontal_output = keras.layers.Conv2D(filters=filters, kernel_size=1)
def _gate(self, x):
tanh_preactivation, sigmoid_preactivation = tf.split(x, 2, axis=-1)
return tf.nn.tanh(tanh_preactivation) * tf.nn.sigmoid(sigmoid_preactivation)
def call(self, input_tensor):
v = input_tensor[0]
h = input_tensor[1]
vertical_preactivation = self.vertical_conv(v)
# Shifting vertical stack feature map down before feed into horizontal stack to
# ensure causality
v_to_h = self.padding(vertical_preactivation)
v_to_h = self.cropping(v_to_h)
v_to_h = self.v_to_h_conv(v_to_h)
horizontal_preactivation = self.horizontal_conv(h)
v_out = self._gate(vertical_preactivation)
horizontal_preactivation = horizontal_preactivation + v_to_h
h_activated = self._gate(horizontal_preactivation)
h_activated = self.horizontal_output(h_activated)
if self.mask_type == 'A':
h_out = h_activated
elif self.mask_type == 'B':
h_out = h + h_activated
return v_out, h_out
综上所述,利用门控块解决了接收域盲点问题,提高了模型性能。
结果对比
原始论文中,PixelCNN使用以下架构:第一层是一个带有7x7过滤器的掩码卷积(a型)。然后使用15个残差块。每个块采用掩码B类的3x3层卷积层和标准1x1卷积层的组合处理数据。在每个卷积层之间,使用ReLU进行激活。最后还包括一些残差链接。
所以我们训练了一个PixelCNN和一个Gated PixelCNN,并在下面比较结果。
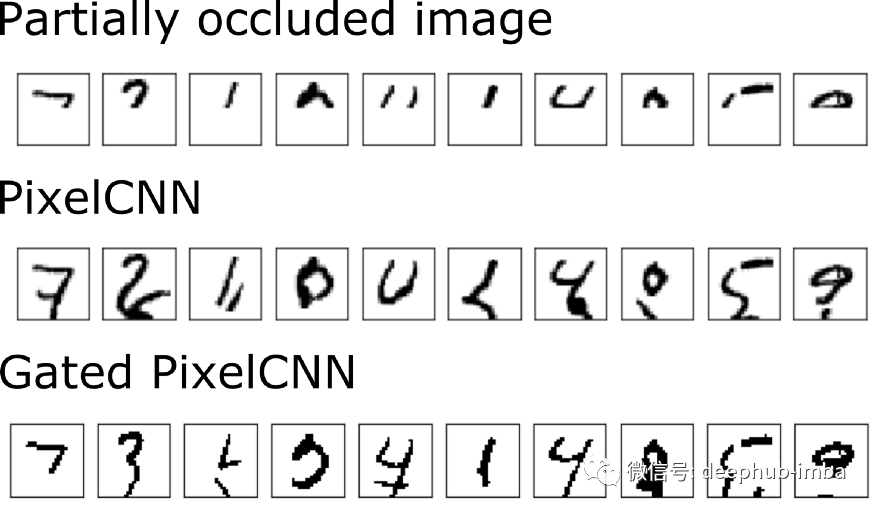
当比较PixelCNN和Gated PixelCNN的MNIST预测时(上图),我们并没有发现到在MNIST上有很大的改进。一些先前被修正的预测数字现在被错误地预测了。这并不意味着pixelcnn表现不好,在下一篇博文中,我们将讨论带门控的PixelCNN++,所以请继续关注!
Gated PixelCNN论文地址:https://arxiv.org/abs/1606.05328
作者:Walter Hugo Lopez Pinaya, Pedro F. da Costa, and Jessica Dafflon