信号处理-小波包分解

文章目录

小波分解与小波包分解

工程应用中经常需要对一些非平稳信号进行，小波分析和小波包分析适合对非平稳信号分析，相比较小波分析，利用小波包分析可以对信号分析更加精细，小波包分析可以将时频平面划分的更为细致，对信号的高频部分的分辨率要好于小波分析，可以根据信号的特征，自适应的选择最佳小波基函数，比便更好的对信号进行分析，所以小波包分析应用更加广泛。
小波包分解（Wavelet Packet Decomposition），又称为最优子带树结构（Optimal Subband Tree Structuring）正是对小波变换的进一步优化。其主要的算法思想是：在小波变换的基础上，在每一级信号分解时，除了对低频子带进行进一步分解，也对高频子带进行进一步分解。最后通过最小化一个代价函数，计算出最优的信号分解路径，并以此分解路径对原始信号进行分解。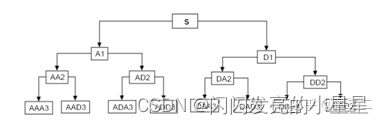

①小波分解
小波变换只对信号的低频部分做进一步分解，而对高频部分也即信号的细节部分不再继续分解，所以小波变换能够很好地表征一大类以低频信息为主要成分的信号，不能很好地分解和表示包含大量细节信息（细小边缘或纹理）的信号，如非平稳机械振动信号、遥感图象、地震信号和生物医学信号等。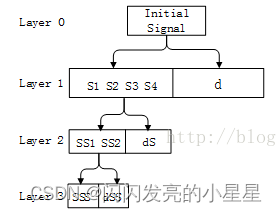

②小波包分解
小波包变换既可以对低频部分信号进行分解，也可以对高频部分进行分解，而且这种分解既无冗余，也无疏漏，所以对包含大量中、高频信息的信号能够进行更好的时频局部化分析。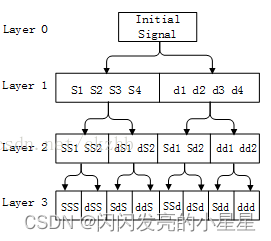

小波包-小波包树与时频图

小波包树解读：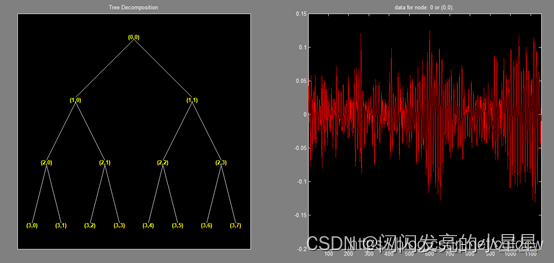

以上即是小波包树，其中节点的命名规则是从（1，0）开始，叫1号， （1，1）是2号………依此类推，（3，0）是7号，（3，7）是14号。 每个节点都有对应的小波包系数，这个系数决定了频率的大小，也就是说频率信息已经有了，但是时域信息在哪里呢？ 那就是 order。 这个order就是这些节点的顺序，也就是频率的顺序。

小波包分解系数

在数值分析中，我们学过内积，内积的物理含义：两个图形的相似性，若两个图形完全正交，则内积为0，若两个图形完全一样，则系数为1（相对值）。小波变换的实质是：原信号与小波基函数的相似性。小波系数就是小波基函数与原信号相似的系数。

连续小波变换：小波函数与原信号对应点相乘，再相加，得到对应点的小波变换系数，平移小波基函数，再计算小波函数与原信号对应点相乘，再相加，这样就得到一系列的小波系数。对于离散小波变换（由于很多小波函数不是正交函数，因此需要一个尺度函数）所以，原信号函数可以分解成尺度函数和小波函数的线性组合，在这个函数中，尺度函数产生低频部分，小波函数产生高频部分

信号的能量

python 实例

小波包的使用

2.1 导入相关的包
下面的导入的包中主要是pywt和matplotlib

import numpy as np
import matplotlib.pyplot as plt
import os
from sklearn import preprocessing
import pywt
import pywt.data
import pandas as pd

2.2 小波包各节点按照频率由低到高

wp = pywt.WaveletPacket(data=tr, wavelet='db1',mode='symmetric',maxlevel=3)#根据频段频率（freq）进行排序print([node.path for node in wp.get_level(1,'freq')])print([node.path for node in wp.get_level(2,'freq')])print([node.path for node in wp.get_level(3,'freq')])

代码中tr表示输入的一维数据，执行结果如下

[‘a’, ‘d’]
[‘aa’, ‘ad’, ‘dd’, ‘da’]
[‘aaa’, ‘aad’, ‘add’, ‘ada’, ‘dda’, ‘ddd’, ‘dad’, ‘daa’]
2.3 打印小波家族

pywt.families()#pywt.families(short=False)

执行结果如下：

[‘haar’, ‘db’, ‘sym’, ‘coif’, ‘bior’, ‘rbio’, ‘dmey’, ‘gaus’, ‘mexh’, ‘morl’, ‘cgau’, ‘shan’, ‘fbsp’, ‘cmor’]
2.4 小波包的分解
（1）小波包分解中关键方法：

wp = pywt.WaveletPacket(data=tr, wavelet='db1',mode='symmetric',maxlevel=3)

该方法输入原始信号tr， 小波函数’db1’，模式’symmetric’，以及最大的分解层数为3。返回wp是小波包树，根据小波包树我们可以提取分解系数。

（2）提取分解系数：

 下面aaa是小波包变换第三层第一个的分解系数

aaa = wp['aaa'].data 
      所以可以使用下面的方法提取每一层的每个节点的小波系数，当然这个方法不太方便，需要一个一个的写，后面有更好的方法：

a = wp['a'].data #第1个节点
d = wp['d'].data #第2个节点#第二层
aa = wp['aa'].data 
ad = wp['ad'].data 
dd = wp['dd'].data 
da = wp['da'].data 
#第三层
aaa = wp['aaa'].data 
aad = wp['aad'].data 
ada = wp['add'].data 
add = wp['ada'].data 
daa = wp['dda'].data 
dad = wp['ddd'].data 
dda = wp['dad'].data 
ddd = wp['daa'].data 

（3） 作小波树图，下面代码中没有优化，后面做了优化：

plt.figure(figsize=(15,10))
 
plt.subplot(4,1,1)
plt.plot(tr)#第一层
plt.subplot(4,2,3)
plt.plot(a)
plt.subplot(4,2,4)
plt.plot(d)#第二层
plt.subplot(4,4,9)
plt.plot(aa)
plt.subplot(4,4,10)
plt.plot(ad)
plt.subplot(4,4,11)
plt.plot(dd)
plt.subplot(4,4,12)
plt.plot(da)#第三层
plt.subplot(4,8,25)
plt.plot(aaa)
plt.subplot(4,8,26)
plt.plot(aad)
plt.subplot(4,8,27)
plt.plot(add)
plt.subplot(4,8,28)
plt.plot(ada)
plt.subplot(4,8,29)
plt.plot(dda)
plt.subplot(4,8,30)
plt.plot(ddd)
plt.subplot(4,8,31)
plt.plot(dad)
plt.subplot(4,8,32)
plt.plot(daa)

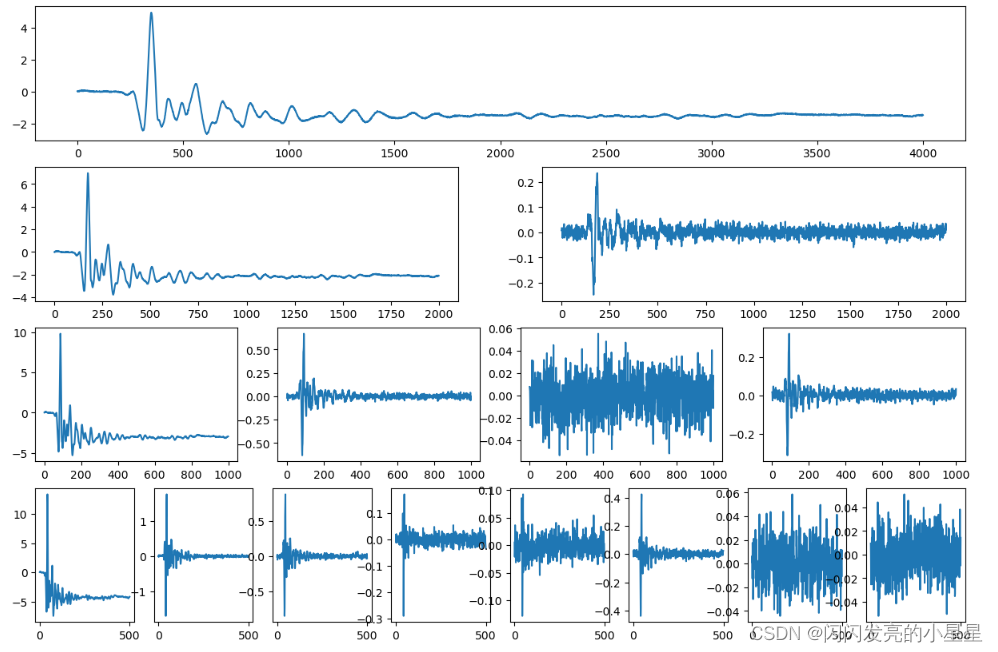
（4） 代码优化，使用的wpd_plt(signal,n)将上面的代码优化和封装了，signal代表输入信号，n代表分解层数：

defwpd_plt(signal,n):#wpd分解
    wp = pywt.WaveletPacket(data=signal, wavelet='db1',mode='symmetric',maxlevel=n)#计算每一个节点的系数，存在map中，key为'aa'等，value为列表map={}map[1]= signal
    for row inrange(1,n+1):
        lev =[]for i in[node.path for node in wp.get_level(row,'freq')]:map[i]= wp[i].data
 
    #作图
    plt.figure(figsize=(15,10))
    plt.subplot(n+1,1,1)#绘制第一个图
    plt.plot(map[1])for i inrange(2,n+2):
        level_num =pow(2,i-1)#从第二行图开始，计算上一行图的2的幂次方#获取每一层分解的node：比如第三层['aaa', 'aad', 'add', 'ada', 'dda', 'ddd', 'dad', 'daa']
        re =[node.path for node in wp.get_level(i-1,'freq')]for j inrange(1,level_num+1):
            plt.subplot(n+1,level_num,level_num*(i-1)+j)
            plt.plot(map[re[j-1]])#列表从0开始  

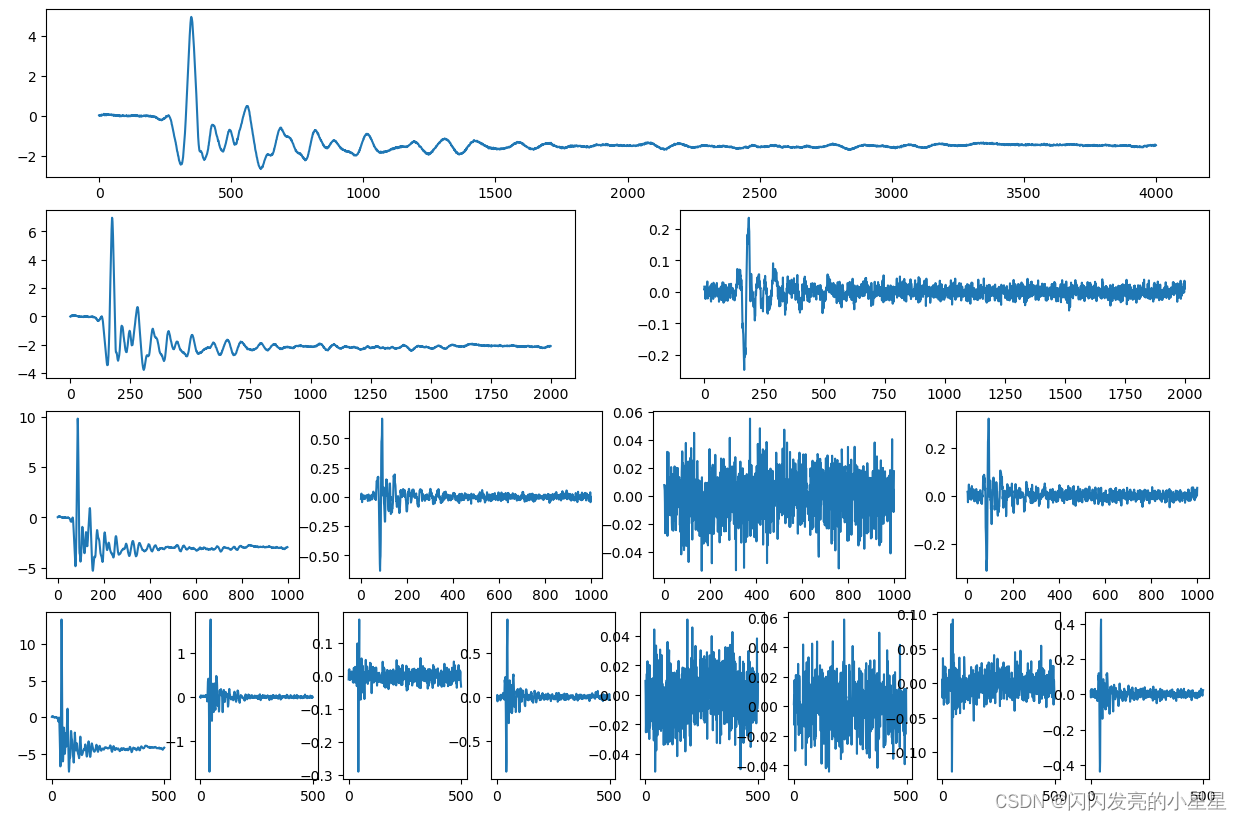
2.5 小波包能量特征提取

n =3
re =[]#第n层所有节点的分解系数for i in[node.path for node in wp.get_level(n,'freq')]:
    re.append(wp[i].data)#第n层能量特征
energy =[]for i in re:
    energy.append(pow(np.linalg.norm(i,ord=None),2))#for i in energy:

 绘制小波能量特征柱形图，注意这里的节点顺序不是自然分解的顺序，而是频率由低到高的顺序：

# 创建一个点数为 8 x 6 的窗口, 并设置分辨率为 80像素/每英寸
plt.figure(figsize=(10,7), dpi=80)# 再创建一个规格为 1 x 1 的子图# plt.subplot(1, 1, 1)# 柱子总数
N =8
values = energy
# 包含每个柱子下标的序列
index = np.arange(N)# 柱子的宽度
width =0.45# 绘制柱状图, 每根柱子的颜色为紫罗兰色
p2 = plt.bar(index, values, width, label="num", color="#87CEFA")# 设置横轴标签
plt.xlabel('clusters')# 设置纵轴标签
plt.ylabel('number of reviews')# 添加标题
plt.title('Cluster Distribution')# 添加纵横轴的刻度
plt.xticks(index,('7','8','9','10','11','12','13','14'))# plt.yticks(np.arange(0, 10000, 10))# 添加图例
plt.legend(loc="upper right")
plt.show()

作图如下：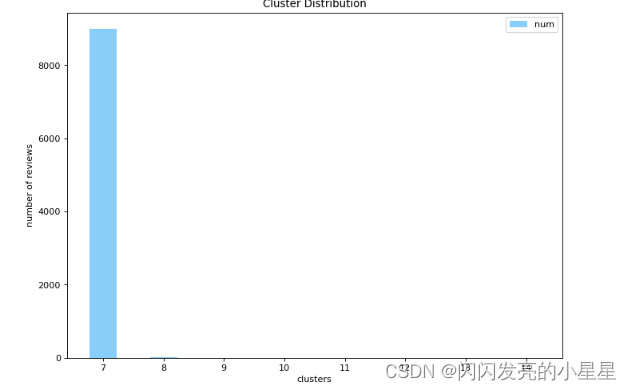

参考

小波与小波包、小波包分解与信号重构、小波包能量特征提取 暨 小波包分解后实现按频率大小分布重新排列(Matlab 程序详解）
小波包变换/能量特征提取/结果图绘制-python代码