初始数据结构

初识集合框架

Java 集合框架 Java Collection Framework ，又被称为容器 container ，是定义在 java.util 包下的一组接口 interfaces和其实现类 classes 。

其主要表现为将多个元素 element 置于一个单元中，用于对这些元素进行快速、便捷的存储 store 、检索 retrieve 、管理 manipulate ，即平时我们俗称的增删查改 CRUD 。。

下面这张图片就是本系列文章 ，所要学习的东西， 比如 ：ArrayList 顺序表， LinkedList 链表，stack 栈， queue 队列， priorityQueue 优先级队列（堆) 等 ，

注意： 这里 只是 列举出了 主要的常用的， 并不是 全部。

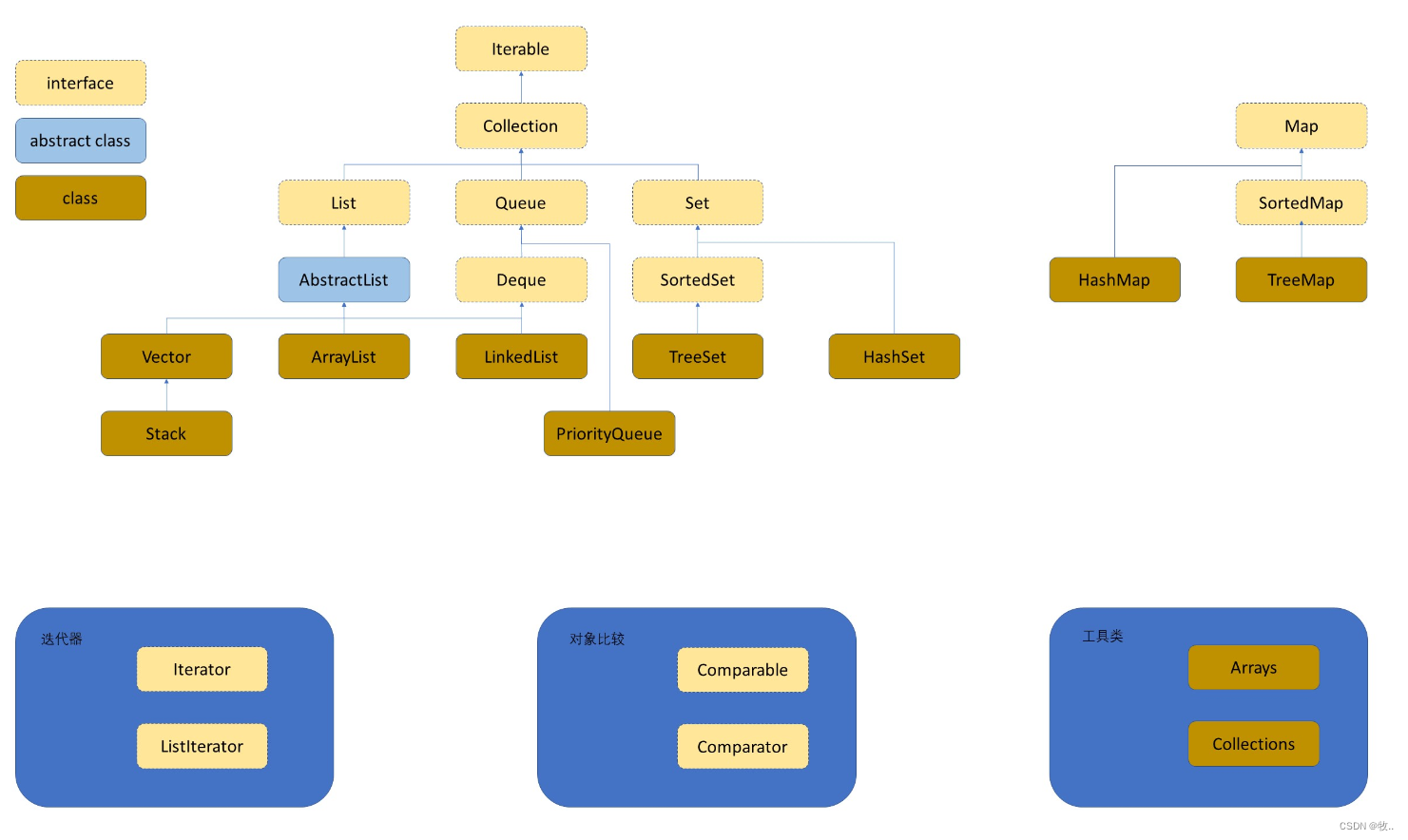
这里我们 想要学习集合， 就需要学习 它背后的数据结构？ 那么 什么是 数据结构？

背后所涉及的数据结构以及算法

问： 什么数据结构？

.数据结构：数据之间的相互关系，即数据的组织形式。

它包括

• 数据的逻辑结构，从逻辑关系上描述数据，与数据存储无关，独立于计算机；
• 数据的存储结构，是逻辑结构用计算机语言的实现，依赖于计算机语言。
• 数据的运算，定义在逻辑结构上，每种逻辑结构都有一个运算集合。常用的运算：检索/插入/删除/更新/排序。

数据结构： 数据 + 结构 描述组织数据的方式

例子： 核酸， 当今我们 没隔几天 我们就需要 做一次核酸， 那么我们需要如何统计每天做核酸的人数呢？

这里就需要 对数据进行组织， 不同的组织方式效率是不一样， 这里就可以通过我们学习过的数据结构，使用当前合适的结构来组织我们的数据 ，提高我们的效率。

说到了数据结构， 那么 算法是 逃不脱干系的， 这里 就在来稍微的介绍一下 算法，

什么是算法：

算法(Algorithm):就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单
来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果

这里我们也不需要太多了解概念，我们只需要 知道拿到一道题目能供清楚他是如何的做出来即可。

那么如何 学好数据结构 和 算法呢？

两个字 死磕即可 。

磕成这样即可 ， 但是我们也是需要 多画图 ， 和多思考的， 同样我们如果遇到了错误，调式也是不可少的。

总结： 多敲多练 多思考 多调试。

看到这里 感觉上面什么都没有 讲 ， 顶多是 了解 了一下 我们 接下来学习啥 ，啥是 数据结构。 没啥营养， 下面就来学习一点有营养的东西，

时间复杂度 or 空间复杂度

学到现在我们 也敲过 很多代码了， 题目也写过不少了把， 那么在我们是如何来判断这个代码（算法）是写的好还是写的坏呢？

1.良好的命名格式（名字取得好）

2.执行的时间块？

3.开辟的空间少？

这里我们一个算法（代码）的好与坏主要分为两部分：时间和 空间。

提出一个问题： 这里 时间 和 空间 那个跟重要？

答案： 都重要， 但是现在我们的时间 会 比 空间 更重要点（注意不是绝对的）。 我记得在我小学的时候，那个时候手机的内存还非常小，那时候我们的内存卡，还比较贵，那么在那个时候 空间就会更重要点， 随着时代的发展我们的内存也越发不值钱， 我们的手机 动不动就是 128(可能还不够)， 256等，所以在当今的角度时间可能就比空间更重要点。

时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个数学函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不

能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复

杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

大O 的渐进表示法

看代码：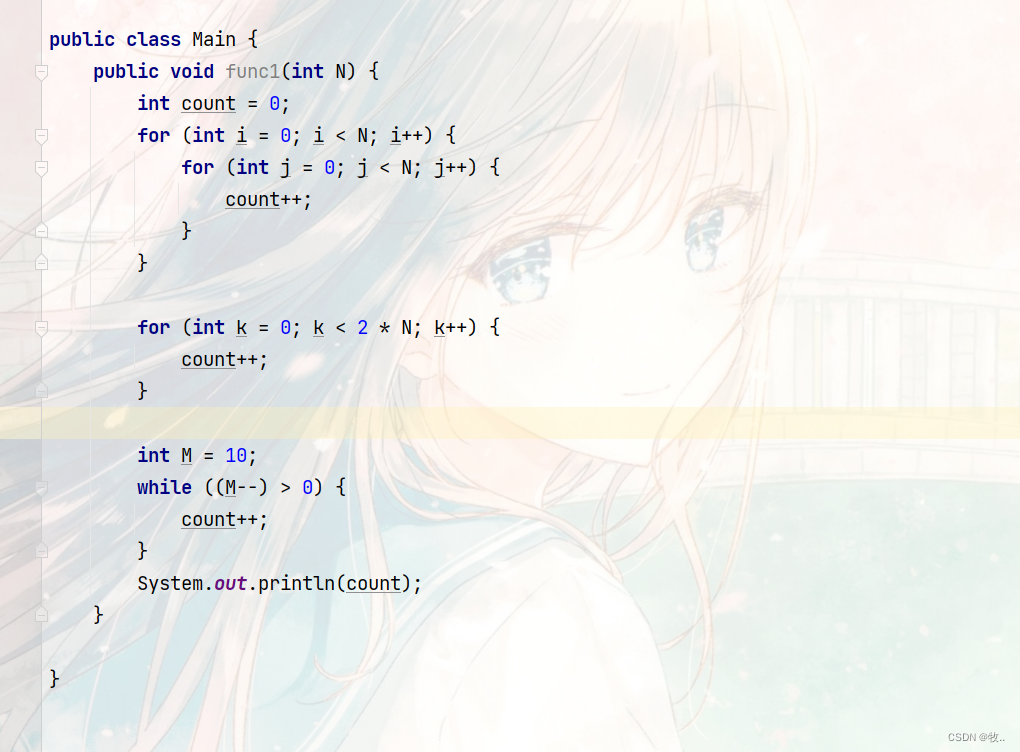

请问： 这里我们的 func1 基本操作执行了 多少次数。

第一个 for 循环 内 嵌套 了 一个 for 循环 ，那么这个 count++ 就 执行了 N * N 次

第二 个 for 循环执行了 2 * N 次

最后我们 有一个 while 循环 执行了 10次.

最终我们能够 算出 我们的 func1 基本执行次数 为： F(N) = N^2 + 2 * N + 10

引出大O的渐进表示法

这里我们思考 一个问题 当我们的 N 越来越大时候， 这里我们的 10 能不能忽略掉呢？

比如： N = 1个亿 ， 那么 1亿 * 1亿 + 2 * 1 亿 这里的 10就 微不足道了， 我们就可以省略。

这里举个现实的例子， 有多少同学在路上看到 1分钱 或者说 1毛钱，会弯下腰捡起来，我想肯定没有几个人会捡， 面值太小，按照现在的物值 啥都买不了， 也就没人捡了， 如果是 100呢？ 我相信 百分百会捡起来的， 不捡白痴吗， 多一百块钱吃顿香的不好吗？

在实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用大O的渐进表示法。

那什么是大O的渐进表示法呢？

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

推导大O阶方法

• 用常数1取代运行时间中的所有加法常数。

上面我们算出 F(N) = N^2 + 2 * N + 10 根据渐进表示法的第一条变为 N^2 + 2 * N + 1

• 在修改后的运行次数函数中，只保留最高阶项。

F(N) = N^2 拿1 亿 举例子 我们 1 亿 * 1亿 那么 2 * 1 亿 + 1 是不是 就 微不足道 了 我们就直接省略。

• 如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

这里 使用完方法 1 和 2，把该做的都做了，还剩 3* N^2, 此时，按照方法3的规则去操作(去掉3*)，最终的时间复杂度为 O(N^2), 即分析这个代码的时间复杂度，在使用大O的渐进表示法以后

最总 我们就能得出上面 那个代码的时间复杂度 为 O(N ^ 2)

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数(下界)

刚刚学习完 大O 的渐进表示法 那么来 练习几个题目 ， 趁热打铁。

题目一：

很明显 这里的 时间复杂度是O(N)

解释： for 循环 得出 执行 2 * N while 循环得出 10次 ， 那么 F(N) = 2 * N + 10 , 那么以大 O 的渐进表示法 不就是 O(N) 吗？

第一条： 常数变为 1 ， 第二条： 保留 最高阶 ， 第三条： 去掉 系数

题目二：

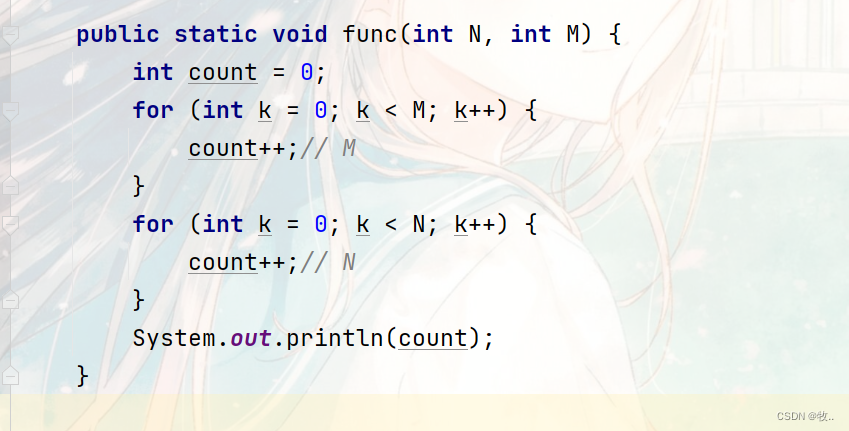
答案： O(M + N)

解释： 第一个循环 执行了 M 次 ， 第二个循环执行了 N 次 ，那么我们的 时间复杂度就为 O(M + N )次， 因为这里我们的M 和 N 是未知 的，并不能合并起来。

题目三：

答案： O(1)

解释：这里我们 for 循环执行了 100次 是常数项 ，那么就可以 表示 为 1， 那么 时间复杂度就为 O(1)

题目四 ： 分析冒泡排序的时间复杂度 ，问： 最好的时间复杂度为？ 最坏的时间复杂度为？

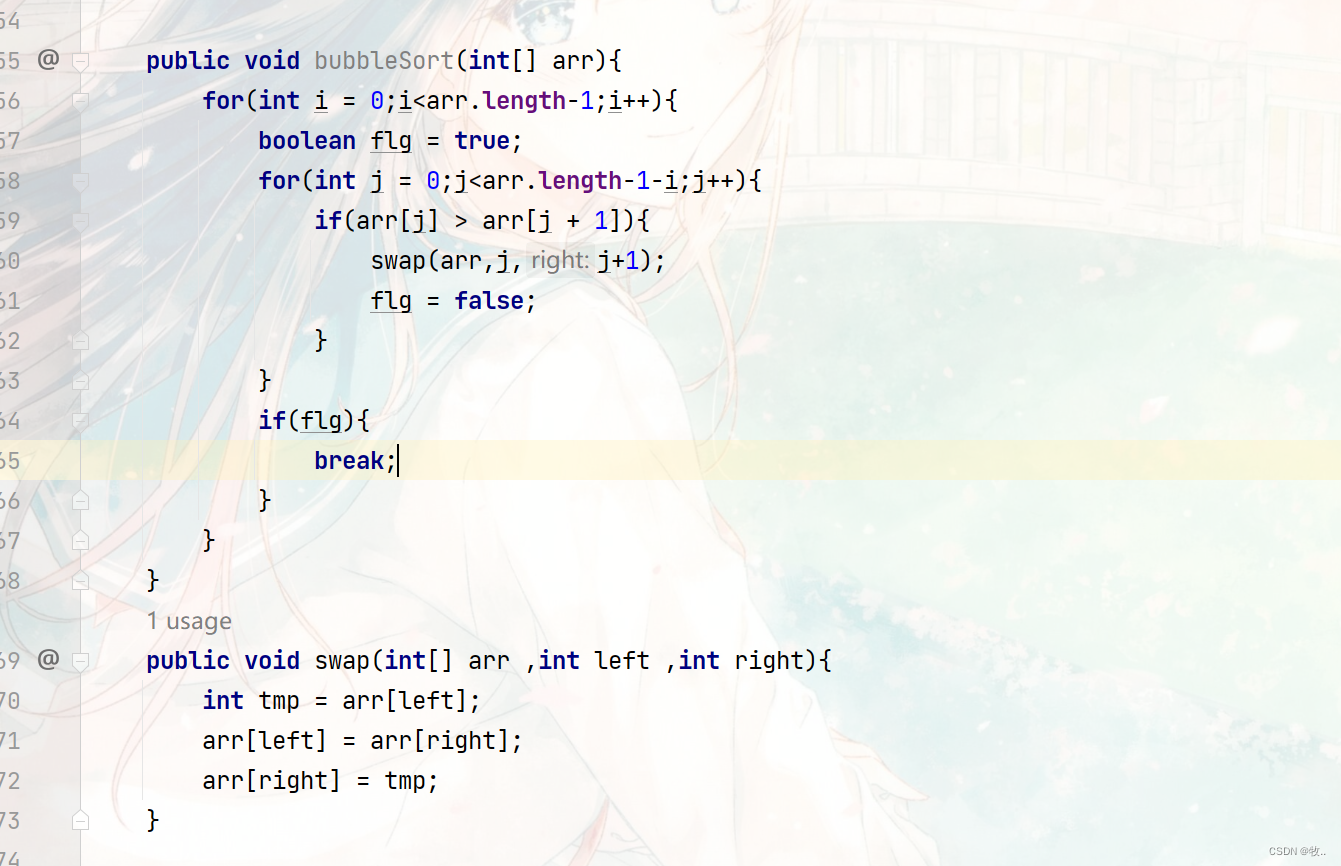
最好 O(N) , 最坏：O(N ^2)

解释： 如果 是 1 2 3 4 5 6 7 这样的 情况下， 在进入 到 内嵌的 for 循环中 就会执行 arr.length - 1 (相当于 N - 1 此时 省略掉 1，就会执行 N 次) 这里 数组是有序的那么 就不会进入 if 语句 flg 就没有机会被改为 false 那么 就会直接 跳出 外层循环， 那么 总共是不是就只执行了 内嵌的 N 次。 这里 最好的情况下 时间复杂度是不是就是O(N)

最坏O(N ^ 2)： 这里 数组 是乱序的

题目五： 二分查找的时间复杂度

答案： O(log n)

解释： 这里我们先来看一下 二分查找的过程(注意：二分使用在有序数组的情况下)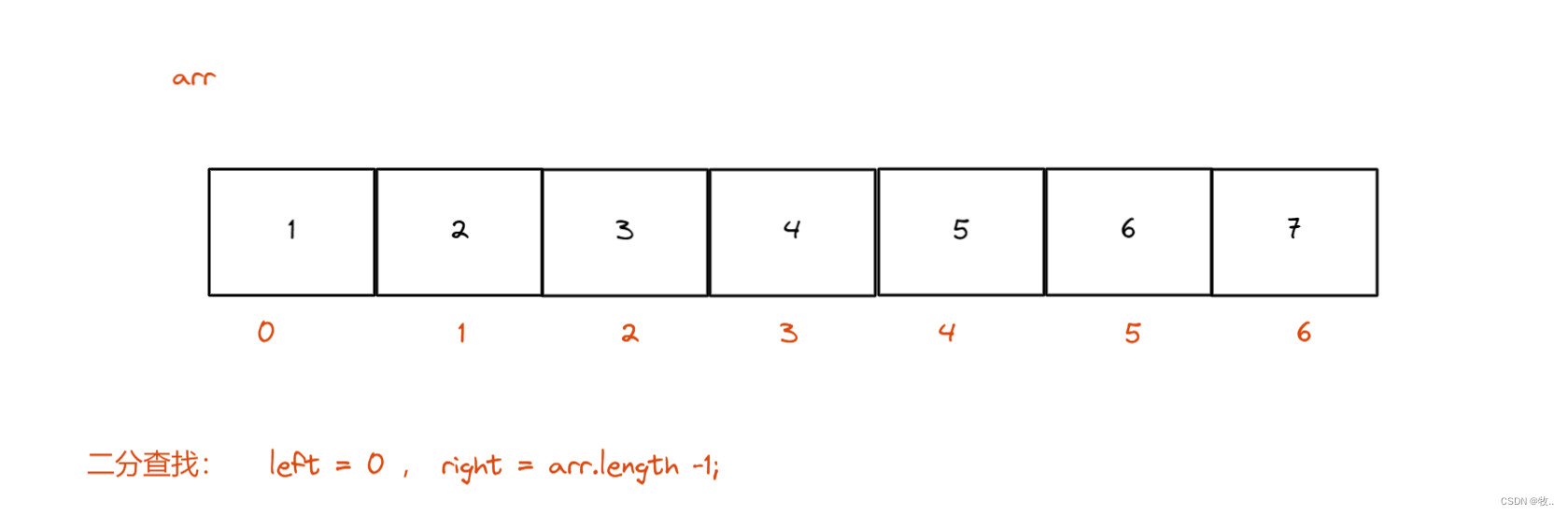

可以看到我们 每次查找 都会减少 一半的 ， 最终我们就能够 推出 时间复杂度为 O(log N)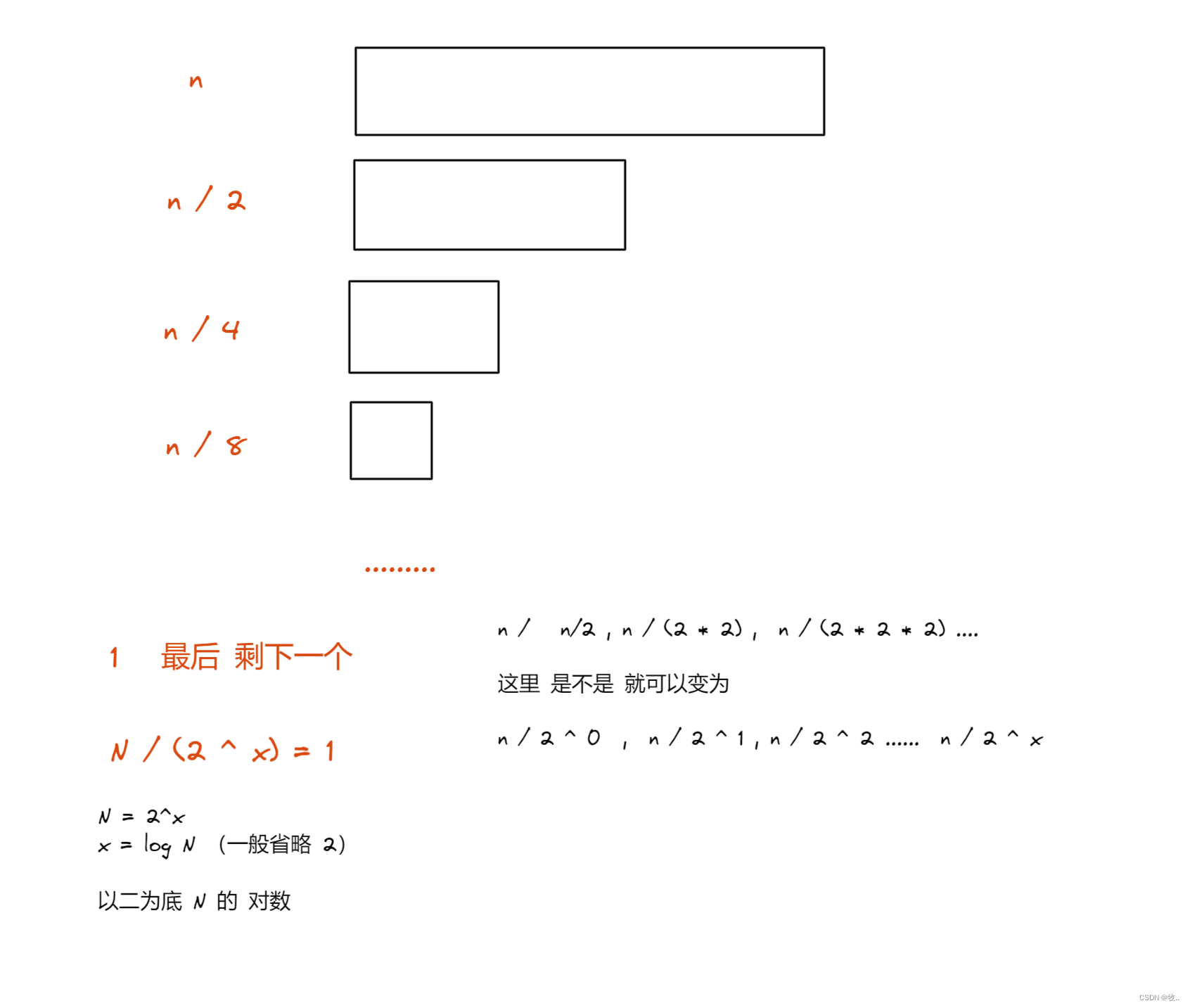

题目六：计算阶乘递归factorial的时间复杂度？

答案： O(N)

解释： 递归的时间复杂度 = 递归的次数 * 每次递归执行的次数

这里我们 每次 执行的 是 一个三目运算符 ， 相当于执行了一次(可以视为常数次)， 只要当我们 的 N = 1 时 才不会 进入方法，那么 时间复杂度是不是 就为 N * 1 就为 O(N)

最后我们来看一个难一点的。

题目七：计算斐波那契递归fibonacci的时间复杂度？

答案： O(2 ^ N)

解释：

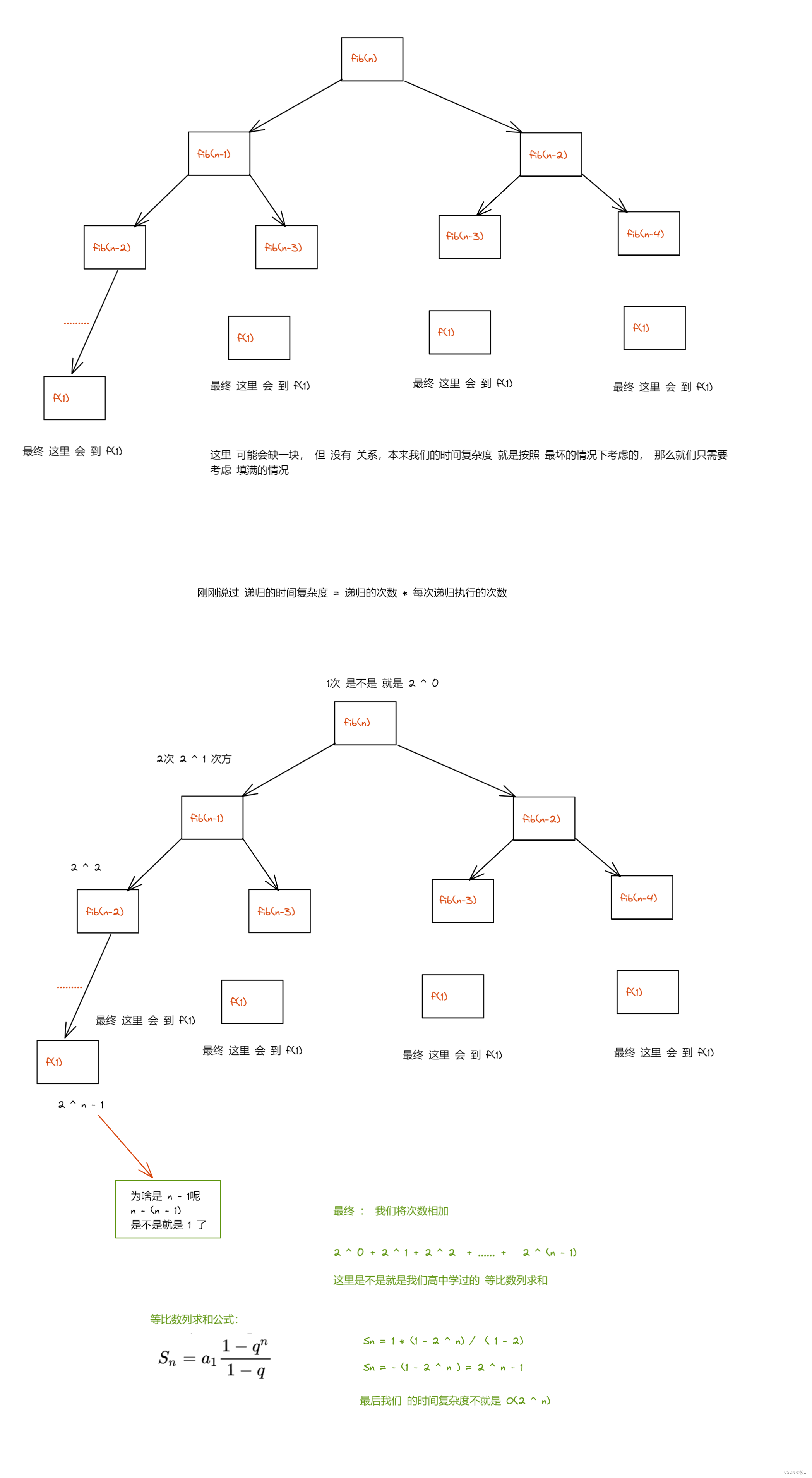
总结：我们的 时间复杂度并不是光靠代码就能给出的， 而是需要通过代码的思想而来获取的

时间复杂度看完我们来 看看 空间复杂度。

空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法

这里 直接通过 实例来 学习 。

题目一： 分析冒泡排序的空间复杂度

答案： O(1)

解释：这里 array数组 并不是 额外的空间，所以不算我们的 空间 复杂度， 我们本来 就是要排序这个数组， 这个数组是我们必须的，所以这个数组是不算的。 这里我们 只有定义了 一个 sorted ， 每次循环都会定义一个，那么这个是不是 就 能算成O(N)呢 这里是不可以的， 在循环中我们每次都会创建一个sorted（之前的哪一个回出了作用域就直接被回收了），到最后我们都只会有一个sorted ，那么这里的 空间复杂度不就是 O(1)。

请问： 我们创建一个拷贝数组 tmp 拷贝 array 完成冒泡排序， 那么 这里的空间复杂度为？

答案： O(N)

解释: 很明显我们多了一个数组 tmp 他的大小 就是 array.length 那么空间复杂度不就是我们的O(N) 吗？

题目二： 求斐波那契数列空间复杂度

答案 ：O(N)

解释： 这里我们 是通过循环来求斐波那契数列的创建了一个 n + 1 的 数组 ，用来放我们的结果， 那么空间复杂度是不是就是O(N + 1) ， 1可以省略那么 就为 O(N) , 那么这里的时间复杂度呢？ 可以看到我们就有一个循环来执行，那么时间复杂度是不是就是 O(N) ,这里使用循环来 求斐波那契数列是比递归要快的 ， 通过时间复杂度进行比较 O(N) 与O（2 ^ N）

题目三：计算阶乘递归Factorial的时间复杂度

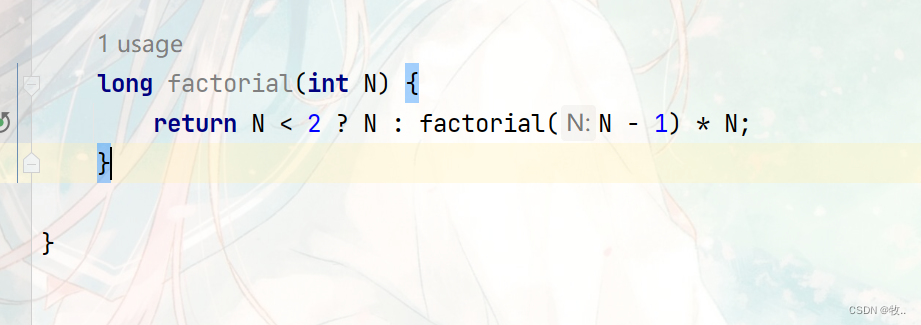
答案： O(N)

解释： 递归的空间复杂度有点不一样。 每递归一次，函数就要在栈上开辟一块空间。 这里每递归一次，空间复杂度为 O(1) 递归N次，空间复杂度为 O(N)

即 阶乘递归函数的空间复杂度为 O(N)

压栈过程：

此时会开辟 N 块空间

最后会弹栈，释放空间。

题目四：

难度升级： 请问：递归求斐波那契数列的空间复杂度是？

解释：

图一：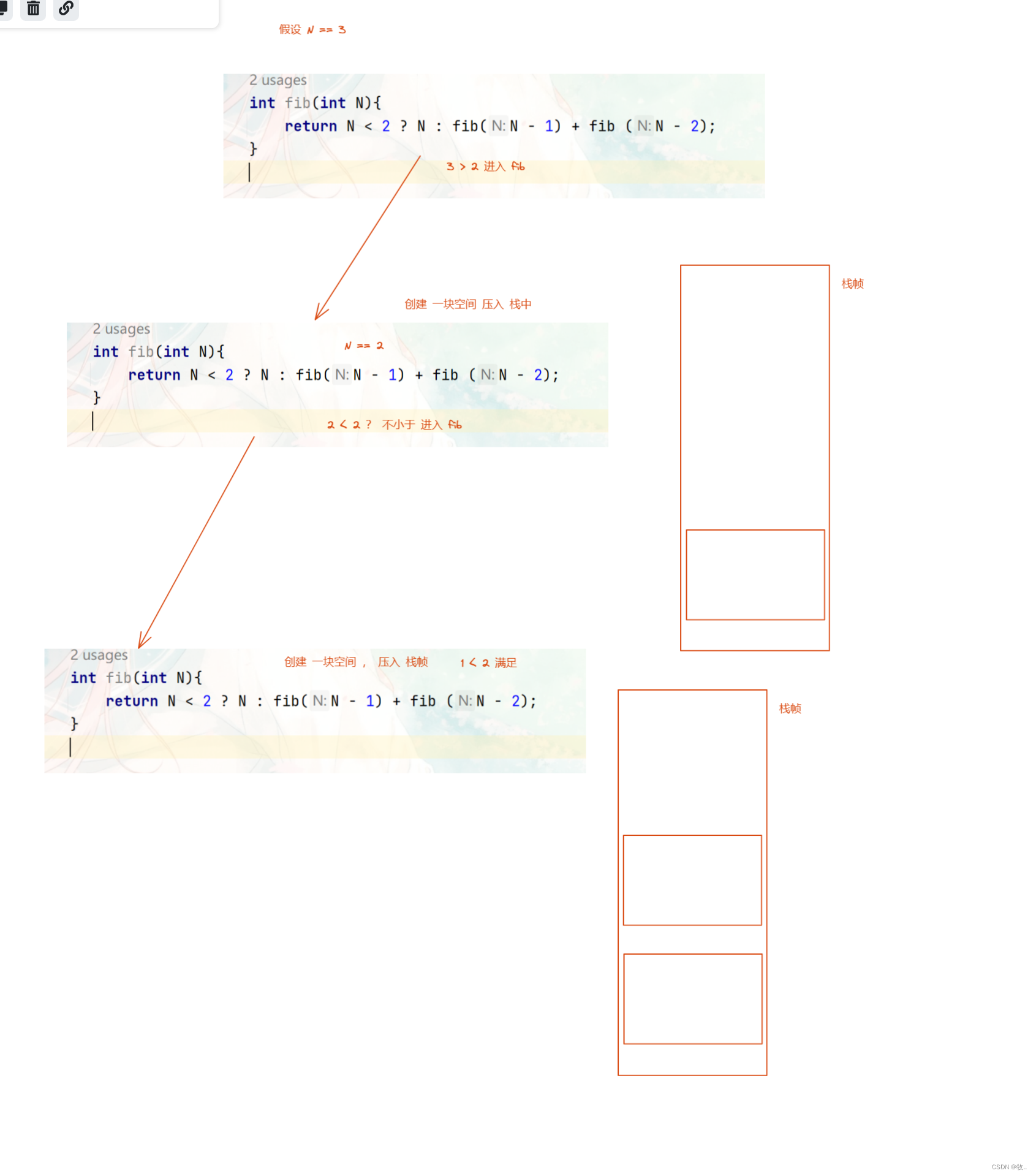

图二：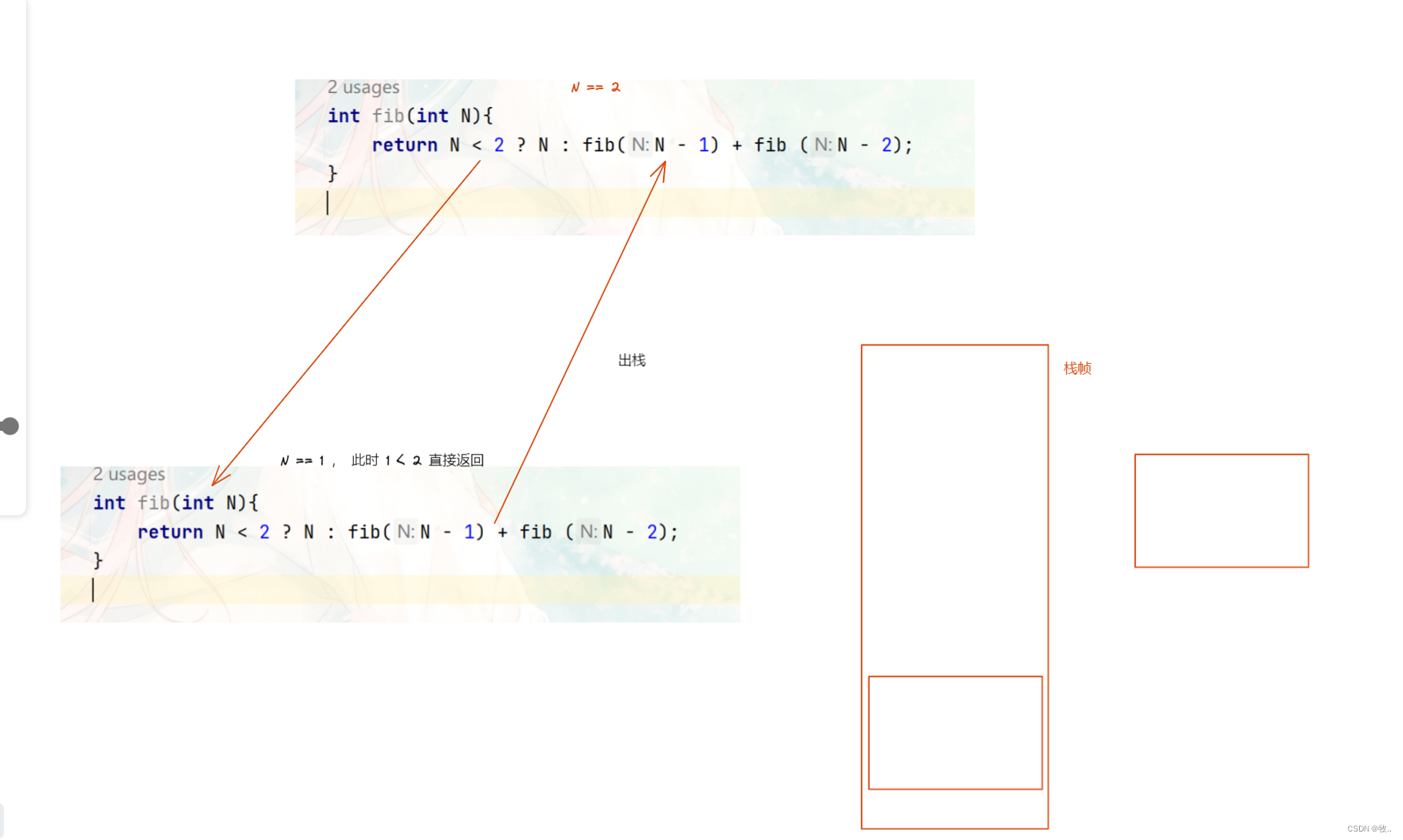

图三：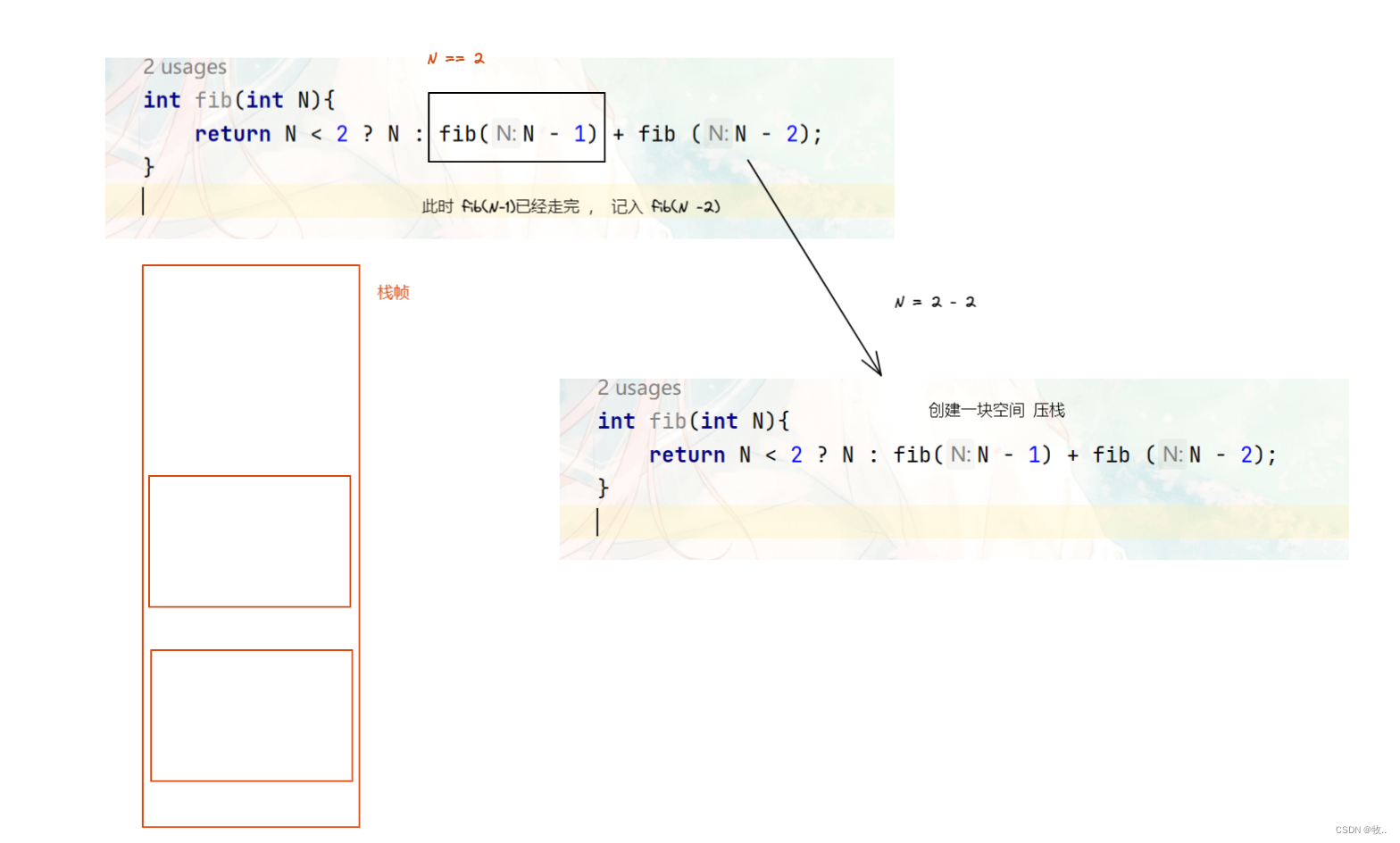

看完上面的 图 我们能明显的知道 ，走完左边就会释放空间，然后走右边， 那么这里最长的路径不就是我们开辟的空间大小吗？

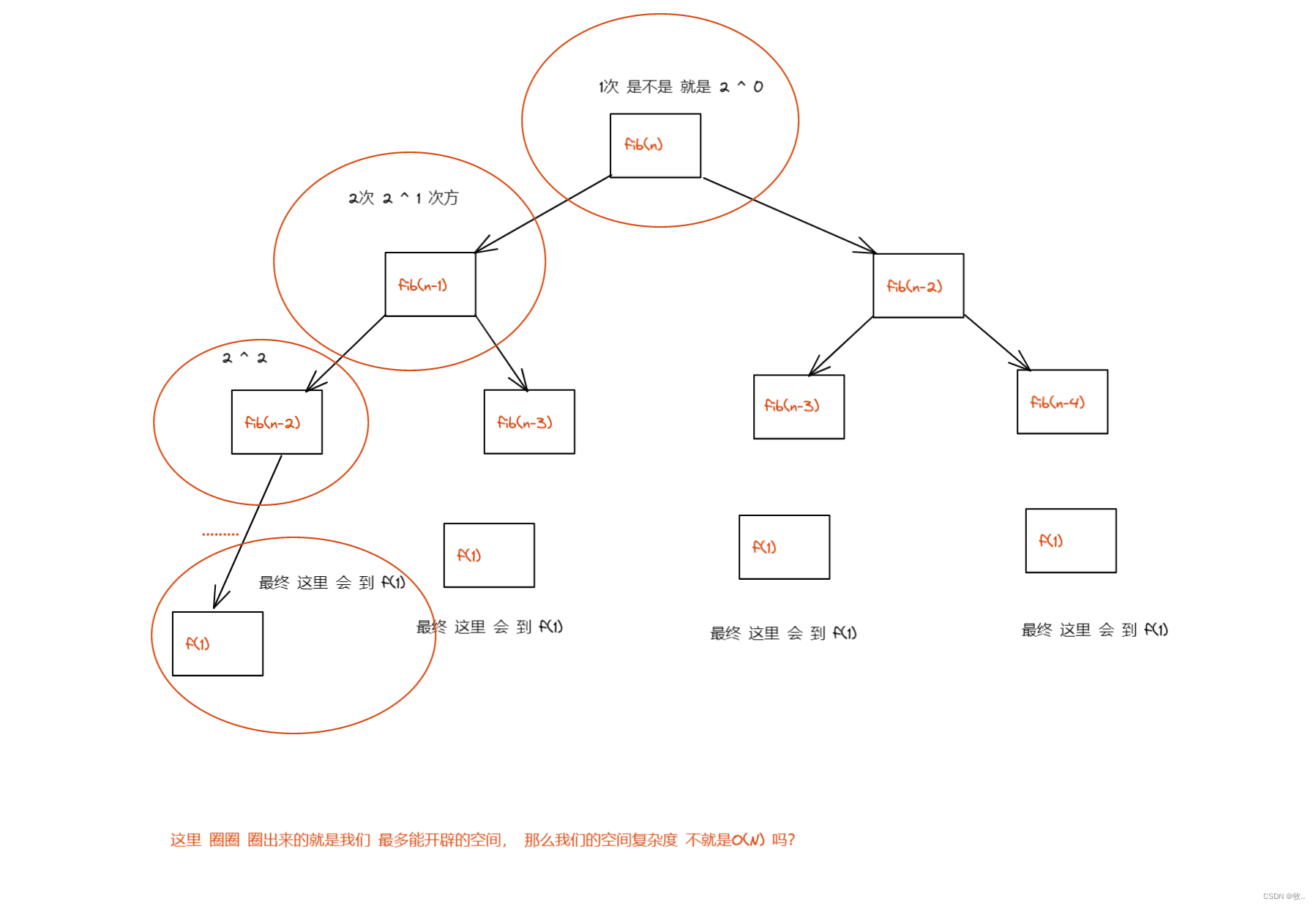
这里我们的时间复杂度 空间复杂度 就学习完 了。 下篇 预告： 泛型。

最后 提供 2个 题目 ， 练练手 ，下篇带上答案：

题目一： 消失的数字

题目二：轮转数组