0
0

结合PCA降维的DBSCAN聚类方法（附Python代码）

目录

前言介绍：

1、PCA降维：

（1）概念解释：

3f361d7fea82414ca1d0245aa2849b0b.pngPCA，全称Principal Component Analysis，即主成分分析。是一种降维方法，实现途径是提取特征的主要成分，从而在保留主要特征的情况下，将高维数据压缩到低维空间。

6f1bdd5bab6a430ab875e12d0707ea00.png在经过PCA处理后得到的低维数据，其实是原本的高维特征数据在某一低维平面上的投影（只要维度较低，都可以视为平面，例如三维相对于四维空间也可以视为一个平面）。虽然降维的数据能够反映原本高维数据的大部分信息，但并不能反映原本高维空间的全部信息，因此要根据实际情况，加以鉴别使用。

（2）实现步骤：

  1.     ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)PCA主要通过6个步骤加以实现：
  3.     1、**标准化**（将原始数据进行标准化，一般是去均值，如果特征在不同量级上，还要将矩阵除以标准差）
  5.     具体：

43c90c21dd574a628e433ed7803e1b5c.bmp

  1.     其中，E为原始矩阵，Emean为均值矩阵，Enorm为标准化矩阵。
  5.     2、**协方差**（计算标准化数据集的协方差矩阵）
  7.     具体：

ae0a75cb6c6546a19b8c0eb5db4188b0.bmp

  1.     其中，Cov为协方差矩阵，m为样本的数量，Enorm为均值矩阵。
  5.     3、**特征量**（计算协方差矩阵的特征值和特征向量）
  7.     具体：
  9.     假设实数λ、n行（原始矩阵E的列数即为n）1列的矩阵X（即n维向量）满足下式：

139b88e78691423d8894128f030be4f7.bmp

  1.     则λ为Cov的特征值，其中Cov为协方差矩阵。
  5.     4、**K 特征**（保留特征值最大的前K个特征（K是降维后，我们期望达到的维度））
  7.     具体：
  9.     若有多个特征值，则保留前K个最大的特征值，以满足之后的计算需求。
  13.     5、**K 向量**（找到这K个特征值对应的特征向量）
  15.     具体：
  17.     通过步骤3中的公式得到每个特征值对应的特征向量。
  21.     6、**得降维**（将标准化数据集乘以该K个特征向量，得到降维后的结果）
  23.     具体：
  25.     ![d845b46e452e48bfbc58e05b706b1c6b.bmp](https://img-blog.csdnimg.cn/d845b46e452e48bfbc58e05b706b1c6b.bmp)
  27.     其中，Epca为最后要求得的PCA降维矩阵，Enorm为标准化矩阵，X1、X2、X3、...、Xk为对K个特征值对应的特征向量。

（3）优劣相关：

  1.     ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)**优点**：   
  3.     1.PCA降维之后的各个主成分之间相互正交，可**消除**原始数据之间**相互影响的因素**。
  5.     2.PCA降维的计算过程并不复杂，因此实现起来**较简单容易**。
  7.     3.在**保留大部分主要信息**的前提下，起到了降维，**简便化计算**效果。
  1.     ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)**缺点**：
  3.     1.特征主成分的定义具有**模糊性**，**解释性差**。
  5.     2.PCA降维选取令原数据在新坐标轴上方差最大的主成分的标准，使得一些方差小的特征较易丢失，**有损失重要信息的可能性**。

2、DBSCAN聚类：

（1）概念解释：

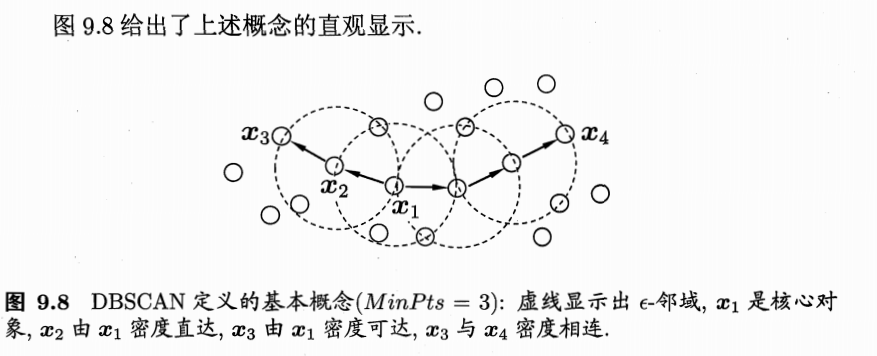
  1.     ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)密度聚类亦称“基于密度的聚类”（Density-Based Clustering）,此类算法假设聚类结构能通过样本分布的**紧密程度**确定。通常情形下，密度聚类算法从样本密度的角度来考察样本之间的**可连续性**，并基于可连接样本不断**扩展聚类簇**以获得最终的聚类结果。
  3.     **DBSCAN**（Density-Based Spatial Clustering of Applications with Noise）就是这样一种聚类算法，该算法基于一组**“领域”**（neighborhood）参数（ε,MinPts）来刻画样本分布的**紧密程度**。

（2）算法原理：

  1.    ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png) 给定数据集D={x1,x2,...,xm}，定义下面这几个概念：

d64d8f508a2848dd8343b3df86a2aa74.png

9fdb9ff77a7642359488cd9932471d10.png

ddc7417999654a0d9338d045b0b42a54.png

b71656162e584be0870332ef8de3dd75.png

9404d3989d51482e903d5d0a21ebc7eb.png

ff93787632564d2b9b9e8885f84f5005.png

  1.      ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)理解了相关概念之后，下面给出算法实现的**伪代码**：

211c9a80f576444b8ef611391279a6b7.png

（3）优劣相关：

  1.           ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)优点：
  3.           1、能够识别**任意形状**的样本。
  5.           2、该算法将具有足够密度的区域划分为簇，并在**具有噪声的空间**数据库中发现任意形状的簇。
  7.           3、**无需指定**簇个数，而是由算法自主发现。
  1.           ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)缺点：
  3.           1、**需要指定**最少点个数（MinPts）与半径（ε）。（但其实相对其他聚类算法来说，已经具有较大的自由性。）
  5.           2、最少点个数与半径对算法的**影响较大**，一般需多次调试。

代码实现：

0、数据准备：

  1.           ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)在这里，我们使用**sklearn库的鸢尾花iris数据集**（sklearn.datasets.load_iris）作为测试数据样本。iris数据集包含**150**个样本，每个样本包含**四个属性特征**（花萼长度、花萼宽度、花瓣长度、花瓣宽度）和一个**类别标签**（分别用0、1、2表示山鸢尾、变色鸢尾和维吉尼亚鸢尾）。
  1.           ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)首先，我们要**安装sklearn库**。安装此库，还是通过pip install命令，但是并不是pip install sklearn，而是**pip install scikit-learn**。正如我们调用opencv是import cv2，而安装却是通过pip install opencv一样。 
  1. pip install scikit-learn
  1.           ![6f1bdd5bab6a430ab875e12d0707ea00.png](https://img-blog.csdnimg.cn/6f1bdd5bab6a430ab875e12d0707ea00.png)然后，获取数据集，其中**x**为鸢尾花的**特征**数据集（数据类型为**数组numpy.adarray**），**y**为鸢尾花的**标签**数据集（数据类型为**数组numpy.adarray**） 。
  1. from sklearn.datasets import load_iris
  2. x = load_iris().data
  3. y = load_iris().target

1、PCA降维：

  1. import numpy as np
  3. def PCA_DimRed(dataMat,topNfeat): #PCA_DimRed--PCA dimension reduction,PCA降维
  4.     meanVals = np.mean(dataMat, axis=0)
  5.     meanRemoved = dataMat - meanVals  # 标准化（去均值）
  6.     covMat = np.cov(meanRemoved, rowvar=False)
  7.     eigVals, eigVets = np.linalg.eig(np.mat(covMat))  # 计算矩阵的特征值和特征向量
  8.     eigValInd = np.argsort(eigVals)  # 将特征值从小到大排序，返回的是特征值对应的数组里的下标
  9.     eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留最大的前K个特征值
  10.     redEigVects = eigVets[:, eigValInd]  # 对应的特征向量
  11.     lowDDatMat = meanRemoved * redEigVects  # 将数据转换到低维新空间
  12.     # reconMat = (lowDDatMat * redEigVects.T) + meanVals  # 还原原始数据
  13.     return lowDDatMat

2、DBSCAN聚类：

  1. import numpy as np
  2. import random
  3. import copy
  5. def DBSCAN_cluster(mat,eps,min_Pts): #进行DBSCAN聚类，优点在于不用指定簇数量，而且适用于多种形状类型的簇
  6.     k = -1
  7.     neighbor_list = []  # 用来保存每个数据的邻域
  8.     omega_list = []  # 核心对象集合
  9.     gama = set([x for x in range(len(mat))])  # 初始时将所有点标记为未访问
  10.     cluster = [-1 for _ in range(len(mat))]  # 聚类
  11.     for i in range(len(mat)):
  12.         neighbor_list.append(find_neighbor(mat, i, eps))
  13.         if len(neighbor_list[-1]) >= min_Pts:
  14.             omega_list.append(i)  # 将样本加入核心对象集合
  15.     omega_list = set(omega_list)  # 转化为集合便于操作
  16.     while len(omega_list) > 0:
  17.         gama_old = copy.deepcopy(gama)
  18.         j = random.choice(list(omega_list))  # 随机选取一个核心对象
  19.         k = k + 1
  20.         Q = list()
  21.         Q.append(j)
  22.         gama.remove(j)
  23.         while len(Q) > 0:
  24.             q = Q[0]
  25.             Q.remove(q)
  26.             if len(neighbor_list[q]) >= min_Pts:
  27.                 delta = neighbor_list[q] & gama
  28.                 deltalist = list(delta)
  29.                 for i in range(len(delta)):
  30.                     Q.append(deltalist[i])
  31.                     gama = gama - delta
  32.         Ck = gama_old - gama
  33.         Cklist = list(Ck)
  34.         for i in range(len(Ck)):
  35.             cluster[Cklist[i]] = k
  36.         omega_list = omega_list - Ck
  37.     return cluster

3、代码汇总：

  1. from sklearn.datasets import load_iris
  2. import numpy as np
  3. import random
  4. import copy
  5. import matplotlib.pyplot as plt
  7. def PCA_DimRed(dataMat,topNfeat): #PCA_DimRed--PCA dimension reduction,PCA降维
  8.     meanVals = np.mean(dataMat, axis=0)
  9.     meanRemoved = dataMat - meanVals  # 标准化（去均值）
  10.     covMat = np.cov(meanRemoved, rowvar=False)
  11.     eigVals, eigVets = np.linalg.eig(np.mat(covMat))  # 计算矩阵的特征值和特征向量
  12.     eigValInd = np.argsort(eigVals)  # 将特征值从小到大排序，返回的是特征值对应的数组里的下标
  13.     eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留最大的前K个特征值
  14.     redEigVects = eigVets[:, eigValInd]  # 对应的特征向量
  15.     lowDDatMat = meanRemoved * redEigVects  # 将数据转换到低维新空间
  16.     # reconMat = (lowDDatMat * redEigVects.T) + meanVals  # 还原原始数据
  17.     return lowDDatMat
  19. def find_neighbor(data,pos,eps): #寻找相邻点函数
  20.     N = list()
  21.     temp = np.sum((data-data[pos])**2, axis=1)**0.5
  22.     N = np.argwhere(temp <= eps).flatten().tolist()
  23.     return set(N)
  25. def DBSCAN_cluster(data,eps,min_Pts): #进行DBSCAN聚类，优点在于不用指定簇数量，而且适用于多种形状类型的簇，如果使用K均值聚类的话，对于这次实验的数据（条状簇）无法得到较好的分类结果
  26.     k = -1
  27.     neighbor_list = []  # 用来保存每个数据的邻域
  28.     omega_list = []  # 核心对象集合
  29.     gama = set([x for x in range(len(data))])  # 初始时将所有点标记为未访问
  30.     cluster = [-1 for _ in range(len(data))]  # 聚类
  31.     for i in range(len(data)):
  32.         neighbor_list.append(find_neighbor(data, i, eps))
  33.         if len(neighbor_list[-1]) >= min_Pts:
  34.             omega_list.append(i)  # 将样本加入核心对象集合
  35.     omega_list = set(omega_list)  # 转化为集合便于操作
  36.     while len(omega_list) > 0:
  37.         gama_old = copy.deepcopy(gama)
  38.         j = random.choice(list(omega_list))  # 随机选取一个核心对象
  39.         k = k + 1
  40.         Q = list()
  41.         Q.append(j)
  42.         gama.remove(j)
  43.         while len(Q) > 0:
  44.             q = Q[0]
  45.             Q.remove(q)
  46.             if len(neighbor_list[q]) >= min_Pts:
  47.                 delta = neighbor_list[q] & gama
  48.                 deltalist = list(delta)
  49.                 for i in range(len(delta)):
  50.                     Q.append(deltalist[i])
  51.                     gama = gama - delta
  52.         Ck = gama_old - gama
  53.         Cklist = list(Ck)
  54.         for i in range(len(Ck)):
  55.             cluster[Cklist[i]] = k
  56.         omega_list = omega_list - Ck
  57.     return cluster
  59. if __name__ == "__main__":
  60.     #1、准备数据
  61.     x = load_iris().data
  62.     y = load_iris().target
  64.     #2、PCA降维
  65.     pro_data = PCA_DimRed(x,2)
  67.     #3、DBSCAN聚类（此步中要保证数据集类型为数组，以配合find_neighbor函数）
  68.     pro_array = np.array(pro_data)
  69.     thecluster = DBSCAN_cluster(pro_array,eps=0.8,min_Pts=30)
  71.     #4、展示降维效果：
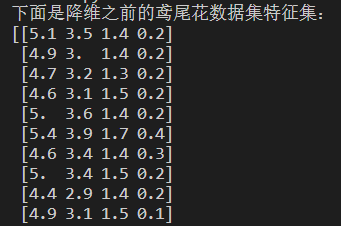
  72.     print("下面是降维之前的鸢尾花数据集特征集：")
  73.     print(x)
  74.     print("下面是降维之后的鸢尾花数据集特征集：")
  75.     print(pro_data)
  77.     #5、展示聚类效果：
  78.     plt.figure()
  79.     plt.scatter(pro_array[:, 0], pro_array[:, 1], c=thecluster)
  80.     plt.show()

实现效果：

1、降维效果：

6f1bdd5bab6a430ab875e12d0707ea00.png降维之前的鸢尾花数据集特征集：

f323b8929b2f44028dfb4f95ce4c8090.png

6f1bdd5bab6a430ab875e12d0707ea00.png降维之后的鸢尾花数据集特征集：

0b682f9e9f654db1b7c446ea66511992.png

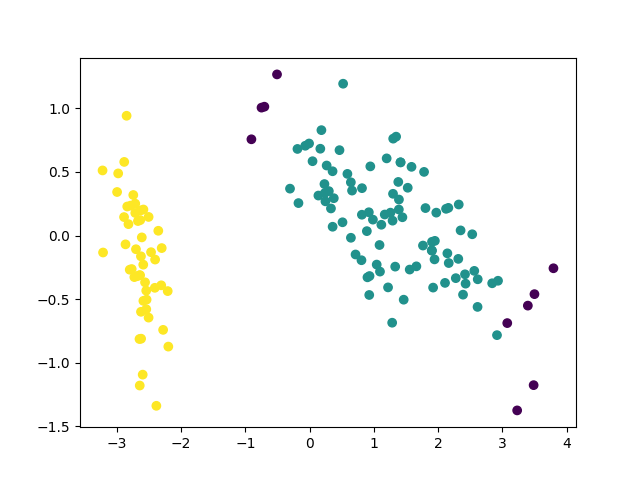
2、聚类效果：

40bf123e9d744fa69a17bbe6dce7f9e1.png

6f1bdd5bab6a430ab875e12d0707ea00.png可以看出来，DBSCAN聚类方法并不能很准确地根据PCA降维后的鸢尾花特征集对鸢尾花样本进行聚类，原因是变色鸢尾与维吉尼亚鸢尾的样本特征较近，两者更类似于同属于一个密度空间，因而导致了该实验的不准确性。

6f1bdd5bab6a430ab875e12d0707ea00.png但是，其实也可以看出，山鸢尾与其他两种鸢尾能够进行较好的区别 ，说明该方法仍适用于不同类别样本间差距较大的聚类情形。

写在最后：

6f1bdd5bab6a430ab875e12d0707ea00.png本篇文章主要介绍了PCA降维、DBSCAN聚类这两个机器学习操作的基本原理，以及两者结合的用于实际数据处理的方法。

6f1bdd5bab6a430ab875e12d0707ea00.png可能基于PCA降维的DBSCAN聚类的方法不是很适用于sklearn库中的鸢尾花数据集，但是该方法既具有处理高维数据的能力，也能够处理各种形状的簇，说明其作为一套较为完整的聚类方法，仍然具有较为广阔的应用场景。

6f1bdd5bab6a430ab875e12d0707ea00.png希望大家能够积极应用这个方法，使得其拥有更多的应用可能性。谢谢各位！

6f1bdd5bab6a430ab875e12d0707ea00.png参考书籍：

周志华.机器学习[M].北京：清华大学出版社，2016.01

6f1bdd5bab6a430ab875e12d0707ea00.png参考文章：

六种常见聚类算法：http://t.csdn.cn/Urhn9

Python PCA(主成分分析法)降维的两种实现：http://t.csdn.cn/NlAeU

DBSCAN聚类算法Python实现：http://t.csdn.cn/lkFhF

PCA降维原理 操作步骤与优缺点：http://t.csdn.cn/QiEJM

46d908c6026d42fd8094221c13854163.png好了以上就是所有的内容，希望大家多多关注，点赞，收藏，这对我有很大的帮助。谢谢大家了！

31deec53974c4aea8cc517b8385f9cf1.gif

1ea540028ba44c97a3c22e18317cf3e9.png好了，这里是Kamen Black 君。祝国康家安，大家下次再见喽！！！溜溜球~~

04eff7ea64b0424599b1579769341f81.jpeg

标签： 聚类 python 机器学习
本文转载自: https://blog.csdn.net/m0_55320151/article/details/130099343
版权归原作者 Kamen Black君 所有， 如有侵权，请联系我们删除。
登录后发布评论

“结合PCA降维的DBSCAN聚类方法（附Python代码）”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

网络安全法-网络运行安全

使用selenium/drissionpage时如何阻止chrome自动跳转http到https

docker desktop 里部署的Open WebUI 管理员密码忘记了的处理方法

在ubuntu20.04中搭建onsite比赛运行环境

利用开源的低代码表单设计器FcDesigner高效管理和渲染复杂表单结构

Kafka学习笔记

【前端】浏览器输入url到页面呈现发生了什么？